Часть II Бесконечность

Множество летающих слонов является подмножеством любого другого полного множества поскольку в нем нет ни одного элемента - одно из следствий Аксиомы регулярности

Бесконечность очень любят математики. Однако физики еще могут стерпеть подразумевающуюся бесконечность вселенной, но приходят в ужас, когда в их уравнениях встречается явная бесконечность. Например, если спросить у физика, что находится внутри черной дыры он, будучи честным, ответит "не знаю", потому что решение уравнения черной дыры выдает в результате ответ, что в ее центре находится бесконечное искривление пространства. Иными словами, как только у физика где-то вместо конкретного ответа получается бесконечность он просто разводит руками и уповает на то, что однажды сможет создать уравнение, которое даст более определенный ответ. В первой части мы с вами уже выяснили, что бесконечность включенная в устройство мироздания приносит с собой много странностей. В бесконечном пространстве произойдет все что возможно по законам физики и произойдет бесконечное число раз, а в бесконечном времени повторится все, что возможно по законам физики и повторится бесконечное число раз. На самом деле в математике с бесконечностью тоже не все в порядке. До 1908 г. математики пытались доказать существование бесконечности, пока Эрнст Цермело не постановил, что доказать или опровергнуть существование бесконечности невозможно. Если нам в наших расчетах нужна бесконечность, то мы должны сделать ее аксиомой^[96].

Напомню, что такое аксиомы. Это утверждения, принимаемые без доказательств, на их основе строится вся математика и вообще по-сути любая формализация: письменная, устная или мысленная. Например, в геометрии очевидно, что через две точки можно провести только одну прямую. Только вот это нельзя доказать - это аксиома, так есть и всё, смиритесь с этим! И раз уж мы выяснили, что бесконечность это аксиома, то давайте разберемся с природой этих аксиом, ведь и там тоже не все так очевидно.

В начале 20-х годов XX века великий математик Давид Гильберт объявил о программе аксиоматизации математики. Он предложил найти такую систему аксиом, которая могла бы объяснить все в математике, основываясь на которой можно было бы доказать или опровергнуть любую теорему. Гильберт надеялся найти такую систему аксиом, которая могла бы дать ответ на все вопросы в математике или хотя бы доказать, что такая система аксиом существует^[97]. Это имело бы далеко идущие выводы о нашей реальности, поскольку, как известно, математика - царица наук, и любая точная и естественно-научная дисциплина на нее опираются, а физики и вовсе давно ищут единую формулу (так называемую "теорию всего"), по которой может быть построено все мироздание. Любая научная теория могла определятся как верная или нет, если бы мы смогли сформулировать ее на языке формальной математики и прогнать через компьютерную программу, которая на основе этой системы аксиом проверила бы ее истинность.

Чтобы аксиомы успешно выводили бы всю математику к ним предъявлялся ряд требований^[98]:
1) Формальность - для формулировки аксиом и построения на их основе теорем должен быть задан язык состоящий из конечного количества символов. О важности языка, на котором формулируется математика мы уже говорили и еще не раз в дальнейшем к этому обратимся.
2) Непротиворечивость - аксиомы или теоремы основанные на этих аксиомах не должны противоречить друг другу и сами себе. Не должно возникать ситуации, когда некоторое высказывание одновременно и верно и неверно. Тут вроде бы все ясно идем дальше.
3) Независимость - аксиомы не должны пытаться объяснить друг друга. Если одна аксиома объясняется другой, то по сути она избыточна и уже не является аксиомой, а вот если аксиомы взаимозависимы, то это быстро приводит к парадоксам.
4) Разрешимость - доказательство любой теоремы на основе принятых аксиом возможно за конечное число рассуждений. Грубо говоря, теоретически мы можем написать программу, которая за конечное время сможет проверить правильность любой теоремы сформулированной на том же формальном языке, что и аксиомы.
5) Полнота - любое утверждение сформулированное на том же формальном языке, что и аксиомы можно либо доказать, либо опровергнуть. То есть не должно существовать недоказуемых утверждений, как например знаменитый Парадокс лжеца (фраза "Я лгу" не может быть истинной ведь я утверждаю что вру, но и ложной быть не может, поскольку если бы я врал, то из отрицания высказывания получалось бы что я говорю правду. Все дело в том, что утверждение сформулировано в неполной системе аксиом, говорящий не может в одиночку определить врет он или нет).

Однако в 1930 году стало очевидно, что программа Гильберта по аксиоматизации математики обречена на провал, когда другой знаменитый математик Курт Гёдель, доказал что в математике существуют такие области, для которых система аксиом всегда будет неполной, и самое главное эта неполнота будет выражаться в том, что непротиворечивость этих аксиом нельзя будет доказать средствами этой теории^[99]. Получается, что в таких системах аксиом всегда будут возникать утверждения, которые нельзя будет доказать или опровергнуть. Ну а поскольку такие утверждения в рамках теории недоказуемы, то мы не можем быть уверены в том, что они непротиворечивы, то есть не являются одновременно истинными или ложными. Что же это за области математики такие, что требуют подобные неполные системы аксиом? Это все разделы, которые так или иначе касаются бесконечности, и неважно является ли бесконечность аксиомой, как например в теории множеств, или эта бесконечность только подразумевается, как например в арифметике, аксиомы этих разделов обречены на неполноту. Всегда можно сформулировать утверждение, которое будет "сильнее" - так называют математики утверждения, которые нельзя опровергнуть средствами принятых аксиом теории.

Давайте разберем аксиомы арифметики, их еще называют аксиомами Пеано, в честь математика, который их сформулировал. Стоит отметить, что это аксиомы лишь для арифметики первого порядка, но пока не вдавайтесь в смысл того, что это означает, позже я объясню, что значит порядок теории. Здесь и далее строгие формулировки я буду выносить в отдельные приложения, и в большинстве случаев я не буду их упрощать, а буду давать в формальном математическом виде. Пусть это не пугает тех, кто не силен в формальной математике, считайте, что это специальные вставки для продвинутых, даже если вы их пропустите, то не потеряете нить повествования, хотя я настоятельно рекомендую хотя бы вскользь с ними ознакомится и вынести оттуда то, что сумеете понять.

Я думаю особого разъяснения аксиомы арифметики не требуют, кроме разве что аксиомы индукции. Данная аксиома гласит, что любое утверждение выполняющееся для некого натурального числа должно работать и со всеми следующими натуральными числами, но для нуля может работать по-особенному. Однако в определении аксиомы не вполне ясно, что значит утверждение. В математике под утверждением понимают некоторую формулу записанную на языке теории. Но так как в тексте аксиомы не говорится о какой-то конкретной формуле, то мы вольны сами определять эту формулу. Поэтому подобные аксиомы иногда называют схемами, потому что они способоны порождать множество дополнительных аксиом, которые тем не менее должны соотвествовать основному принципу схемы. Например, мы можем определить формулу сложения так: a+0 = a и a+S(b) = S(a+b), а формулу умножения так: a×0 = 0 и a×S(b) = a+(a×b). Данные формулы являются рекурсивными, поскольку основаны на принципе индукции. Ведь раз то что справделиво для n+1, справделиво и для n, следовательно это позволяет формулам выполняться последовательно в обратном порядке, подставляя в себя все предыдущие натуральные числа, пока они не дойдут до нуля, а для нуля в формуле указано особое правило, которое останавливает рекурсию. Получается, что аксиома индукции, как раз и позволяет нам создавать рекурсии в арифметике. И две выше приведенные формулы соотвествуют более привычным нам словесным определениям, что сложение a+b это отсчитывание b раз, начиная от a; и что умножение a×b это сложение a само с собой b раз. В дальнейшем мы еще не раз обратимся к этой аксиоме, и тогда разберем ее особенности подробнее.

Итак, вот она, всем нам знакомая арифметика, которой мы пользуемся каждый день, делая любые расчеты мы не задумываясь сталкиваемся с этими аксиомами и принимаем их как должное. Однако согласно Теореме Гёделя о неполноте эта формальная система аксиом не является полной, и существуют утверждения которые можно сформулировать на языке арифметики, но при этом их нельзя будет доказать или опровергнуть ее средствами^[99]. В частности существует такое число, очень большое число, существование, которого нельзя показать из аксиом арифметики. Хотя это не совсем корректное определение, ведь в предыдущей части мы выяснили, что большие числа сами по себе уже не несут смысла, сравнивать надо не их, а рекурсии, что их создают. Тогда лучше сказать так: существует такая рекурсия для создания сверхбольших чисел, которая невыводима из аксиом арифметики (в частности именно аксиома индукции в своем обычном виде уже не может с ней справится)^[102]. В прошлой части мы даже близко не подошли к уровню этой рекурсии, но не расстраивайтесь все еще впереди, скоро мы познакомимся с числом, которое будет бо́льшим, чем может создать привычная нам школьная арифметика.

Тут нет никаких противоречий, ведь согласно Теореме Гёделя о неполноте должна существовать более "сильная" система аксиом, в которой можно создать рекурсию способную описать такое число, это и докажет непротиворечивость арифметики, но уже не ее средствами как и следует из теоремы о неполноте. Получается, что мы не можем иметь общей системы аксиом для всей математики, у нас может быть несколько независимых систем аксиом, каждая из которых будет объяснять свою область математики, многие среди них, те что касаются бесконечностей, будут неполные (например, не смогут описать какие-то сверхбольшие числа), но всегда будет существовать более "сильная" теория (способная описать эти сверхбольшие числа) и доказать непротиворечивость теорий, которые "слабее" ее. Получается, что разные математические теории способны создавать разные по величине числа, этим и можно определить силу теории. Это очень важное следствие, которое придает важности гугологии, теперь это не просто забава по созданию больших числах, а серьезная область математики, которая может измерить "силу" формальных математических теорий, хотя если честно в математике у этого уже есть и более профессиональное название, чем гугология, этот раздел именуется ординальным анализом^[103].

Теорема Гёделя о неполноте (часть 1). Любая формальная математическая теория, включающая или выводящая арифметику, неполна: в ней существует и может быть эффективно построена формула, такая что будет истинной, но не выводимой из аксиом теории.

Теорема Гёделя о неполноте (часть 2). Для любой непротиворечивой формальной математической теории, включающей или выводящей арифметику, формула, выражающая непротиворечивость теории, недоказуема аксиомами самой теории.

С одной стороны может показаться, что не все еще потеряно по части общей аксиоматизации математики, ведь если более "сильная" теория может описать, то что недоказуемо в слабой, давайте придумаем такую систему аксиом, которая будет самой сильной. Но если вы все правильно поняли из предыдущего абзаца, то понимаете, что такой системы аксиом не может существовать. У каждой системы аксиом, какой бы сильной она не была есть такое сверхбольшое число, которое она не сможет описать, а поскольку не существует самого большого числа, то и не существует самой сильной системы аксиом. Важно понимать, что из аксиом принятой математической системы не следует, что это некое сверхбольшое чиcло не существует, просто в рамках этой системы нет эффективного и лаконичного способа его достижения и понимания. Однако если нам, допустим, нужны лишь аксиомы арифметики, зачем городить лишние более сложные аксиоматические системы, это лишь усложнит расчеты и доказательство теорем. К тому же числа, которые нельзя конструктивно описать аксиомами Пеано уже столь велики, что точно не пригодятся на практике. Значит пока мы не выходим в своих суждениях за рамки принятой аксиоматической системы, то можно смело в ней работать. На этом закончим отступление про аксиомы, ведь мы и так отступили от темы сверхбольших чисел, чтобы поговорить о бесконечности. Но я непросто так делаю все эти ремарки в повествовании, каждая из них очень важна для понимания природы сверхбольших чисел.

Возвращаясь к бесконечности, давайте в начале разберемся, зачем нужна была аксиома, которая объявляет о ее существовании. В арифметике аксиома бесконечности не присутствует, бесконечность как концепция лишь подразумевается, когда мы говорим, что натуральные числа могут бесконечно следовать одно за другим, но мы не можем ее "пощупать", если можно так выразиться, не можем работать с ней, оперировать ей. Арифметика это запрещает, она разрешает работать только с натуральными числами, а бесконечность это не число. Бесконечность - это множество, и раз это слово прозвучало, давайте перейдем к другой ремарке, а именно разберем, что же такое множества.

История возникновения термина связана с именем другого известного математика Георга Кантора. Когда он разрабатывал свою теорию в 1870 году, теорема о неполноте еще не была написана, и Кантор видел в своей теории как раз ту самую основу для всей математики, поисками которой позже занялся Гильберт. В рамках разработанной им теории множеств он показал, что натуральные числа это не самые фундаментальные понятия, их можно вывести из множеств. Так же на основе множеств он вывел объяснение иррациональным числам, и следовательно геометрическим полям. Получается что аксиоматические термины из геометрии, вроде плоскости, прямой или точки - тоже не являлись фундаментальными понятиями, а выводились из множеств^[104]. На тот момент неприятие теории множеств в сообществе математиков было настолько сильным, что некоторые называли ее "болезнью", но именно Давид Гильберт, увидел в ней тот самый инструмент, с помощью которого можно объединить всю математику и провозгласил: "Никто не может изгнать нас из рая, созданного Кантором". Именно на аксиомы теории множеств Гильберт возлагал основные надежды, как на всеобъемлющую систему аксиом.

До Кантора именно геометрию пытались сделать основой для всей математики, эти попытки велись начиная с Евклида и кризиса Пифагорейской школы, которая пыталась объяснить все при помощи натуральных чисел (и для которой закатом стало открытие иррациональных чисел и того что их невозможно было описать арифметически). Однако к середине XIX века стало понятно, что геометрия не может быть основой для всей математики, поскольку этих геометрий несколько, как минимум, кроме геометрии Евклида на тот момент уже были известны геометрия Лобачевского с отрицательной кривизной пространства и геометрия Римана с положительной кривизной пространства (в каждой из этих геометрий была своя аксиома о параллельных прямых)^[105].

1) Геометрия Евклида. На плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
2) Геометрия Римана. Любые две прямые лежащие в одной плоскости являются замкнутыми и пересекаются.
3) Геометрия Лобачевского. Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Все было просто прекрасно, однако формулировка теории, так как описывал ее Кантор сталкивалась с рядом парадоксов, один из которых и вылился в итоге к требованию о полноте системы аксиом, дело в том, что теория Кантора, Наивная теория множеств (как ее позже назовут), создавала одну парадоксальную сущность, от которой не могла отделаться, которую называли множеством всех множеств. Что же это за гадость такая? Множество всех множеств - это абстрактное абсолютнейшее множество, которое включает в себя вообще все, что только возможно, мыслимо и немыслимо. Однако существование такого множества делает теорию множеств противоречивой. В историю это противоречие вошло, как парадокс Рассела, в честь математика Бертрана Рассела, который его сформулировал^[106].

Парадокс на самом деле весьма прост и звучит так: если существует множество всех множеств, то куда входит это множество. Для наглядности парадокса было придуманы всякие неразрешимые загадки. Наиболее часто в качестве иллюстрации парадокса используется задачка про брадобрея. В одном городе был издан указ, что брадобрей может брить только тех кто не бреется сам. Тогда встает вопрос: как ему быть с самим собой, ведь если он побреет себя, то получается он побреет того, кто бреется сам, что делать запрещено. Но если он не будет себя брить, то окажется среди тех, кто сам не бреется, значит является сам для себя клиентом. Другая версия наглядного выражения парадокса имеет религиозные аллюзии: Бог не может быть всемогущим, поскольку не может создать что-то что ограничивало бы его могущество, ведь в противном случае он бы не был всемогущим. Но мне больше всего нравится третья версия парадокса, на мой взгляд ассоциация с множеством всех множеств в ней наиболее близкая. Существует страна, в которой есть три закона: все жители должны жить в городах, в каждом городе должен быть мэр, мэр не может жить в одном городе со своими горожанами. Казалось бы, очевидным решением было создать отдельный город для мэров - но вот незадача, где будет жить мэр города мэров?

Выходом из ситуации было создание системы аксиом, которые бы запрещали возникновение такой сущности, как множество всех множеств. На самом деле с этим справляется одна аксиома - аксиома бесконечности, другие ей просто помогают. Современная наиболее распространенная формулировка аксиом теории множеств называется ZFC (Zermelo-Fraenkel and axiom of Choice - Аксиомы Цермело и Френкеля, плюс Аксиома выбора). Все же надежды Кантора и Гильберта, который тоже ставил на теорию множеств, не сбылись. Никакая аксиоматическая система включающая или выводящая из себя арифметику не может быть полной, это следует из теоремы о неполноте Гёделя, и ZFC не исключение из этого правила. Существуют утверждения, которые недоказуемы в рамках ZFC (с одним важным из них мы еще познакомимся), так же существуют сверхбольшие числа, рекурсии для создания которых не могут быть описаны в рамках ZFC (размер этих чисел воистину непостижим, он намного, намного больше чем числа, что не может описать арифметика, даже я в рамках этой книги не смогу полностью показать масштаб таких рекурсий, хоть и попытаюсь сравнительными прыжками до него дойти). В общем так же как и с геометриями, получается что теория множеств не одна, их много и каждая содержит какие-то свои аксиомы, некоторые из теорий множеств "сильнее", некоторые "слабее", но абсолютной теории множеств, которая описала бы все, что есть в математике, не существует, так же как не существует самого большого числа. Бывает, что из разных аксиоматических систем можно вывести все те же теоремы что и из других, но бывает что теоремы выводимые в одних аксиоматических системах могут противоречить теоремам выводимым в других аксиоматических системах, даже если они равны по силе. С другими аксиоматическими системами теории множеств мы еще познакомимся, пока нам как и большинству математиков работающих с множествами достаточно будет ZFC. Поэтому я предлагаю здесь подробно разобрать её аксиомы.

Тех, кто бегло ознакомился с приложением и ничего в нем не понял, я спешу успокоить, сейчас мы все это разберем подробно, понятно и упрощенно. Нам для постижения сверхбольших чисел, в дальнейшем понадобится знание каждой аксиомы теории множеств. Начнем с того, что само понятие множества - неопределяемое, это нечто, о чем мы можем помыслить, или если немного красивее выразиться: то это когда из нашего необузданного ментального мира мысль выхватывает некую формальную абстракцию. Множество может содержать элементы и это есть нечто больше, чем совокупность элементов его составляющих. Такое определение относит нас к Аристотелю, который утверждал, что система это нечто больше чем совокупность ее составляющих, этот принцип, называемый эмерджентностью, очень важен в физике, и так же является краеугольным камнем в теории множеств^[109]. Ну и самое главное, что следует уяснить, множество - это не число, а более фундаментальное понятие. Понимаю, что многим сложно отказаться от чисел, особенно когда речь идет о математике, но попробуйте забыть, что вы знаете, что такое число, пока мы обсуждаем аксиомы теории множеств.

Итак первая аксиома утверждает, что существует пустое множество - это не просто абстракция, а абстракция всех абстракций, множество не содержащее элементов. Тут нет никаких противоречий, ведь множество образуются когда мы можем помыслить о чем-то, но ведь мы так же можем помыслить о пустоте, о чем-то таком в чем не содержится никаких элементов. Далее идет один важный вывод, пустота всегда одинакова, это всегда "ничто", а значит пустое множество обозначаемое значком ø, тоже всегда единственно, и всегда одно такого рода.

Вторая аксиома утверждает, что любое множество может быть подмножеством. Главный вывод, который отсюда следует, множества могут иметь отношения и вступать во взаимодействия, образуя новые множества. Простейшие примеры таких взаимодействий, это собственно существование подмножеств a⊂b - рисунок №28, например {x,y}⊂{w,x,y,z}; а так же пересечение множеств с = a⋂b  - рисунок №29, например {w,x} = {w,x,y,z}⋂{u,v,w,x}; и объединение множеств с = a∪b - рисунок №30, например {v,w,x,y,z} = {v,w,x}⋂{x,y,z}.

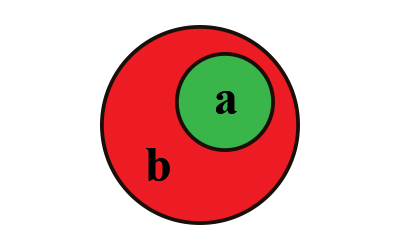
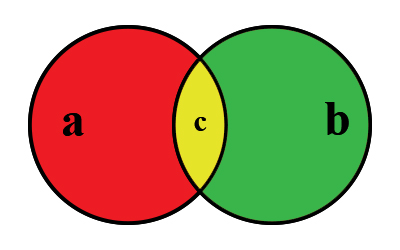
Третья аксиома четко разграничивает понятие элемент и подмножество, согласно ей множество может быть само себе подмножеством, но не может содержать самого себя как элемент. Из нее напрямую следует вывод, что пустое множество является подмножеством любого множества, но не элементом. Например, в множестве {a,b,c} есть три элемента a, b и с и так же в этом множестве можно выделить восемь подмножеств: собственно пустое ø = {} и множества {a}; {b}; {c}; {a,b}; {a,c}; {b,c}; {a,b,c}. Странный вывод можно сделать на основе этой аксиомы, получается, что например множество всех летающих слонов является подмножеством для множества всех нобелевских лауреатов, ведь летающих слонов не бывает, и значит множество летающих слонов пустое, а любое множество содержит пустое множества в качестве подмножества.

Четвертая аксиома очень простая и не нуждается в разъяснениях, два множества содержащие одни и те же элементы, действительно, в сущности являются одним и тем же множеством, например {a,b,c} = {a,b,c}. Основное ее следствие в том, что у множеств нет других характеристик, которые не связаны с элементами находящимися в них. Множества нельзя сравнить с коробками, скорее это некая абстрактная мыслеформа, у которой нет каких-либо собственных свойств не связанных с ее содержимым.

Пятая аксиома утверждает, что множества можно использовать как элементы для построения других множеств. Например, если есть два множества {a,b} и {b,c}; значит и есть множество {{a,b},{b,c}}; которое смею заметить не равно множеству {a,b,c}, ведь элементы a, b и с идут в нем в составе других множеств.

Вот мы и добрались до аксиомы бесконечности, я специально включил ее в список шестой, а не первой, потому что для ее разбора потребуется понимание всех предыдущих аксиом. Начнем с того, что как раз эта аксиома определяет существование натуральных чисел, именно с ее помощью мы выводим понятие натурального числа из понятия множества. В арифметике сущность натуральных чисел не описывается, подразумевается что у нас всегда есть что считать, числа просто необходимо ассоциировать с какими-то объектами, так же как это делали первобытные люди когда у них формировалось понятие числа, они могли считать камни, деревья, животных. Но наша задача определить число из чистой абстракции, не используя никаких материальных объектов. Так что же мы будем считать, если у нас нет ничего, так вот с этого "ничего" мы и начнем, вернее с пустого множества, которое в теории множеств как раз и ассоциировано с "ничем". Вот мы помыслили о пустоте и создали пустое множество ø, пуcть это будет 0. Дальше, будьте внимательны, мы уже можем помыслить об этом пустом множестве, создав новое множество, которое содержит пустое в качестве элемента {ø}, пуcть это будет 1. И теперь у нас уже есть два объекта о которых можно мыслить: о пустом множестве ø и о множестве содержащем это пустое множество {ø}, получаем множество, которое содержит их обоих как элементы {ø,{ø}} и это будет 2. Затем помыслим о множестве, которое содержит пустое множество ø, множество содержащее пустое множество {ø}, и множество содержащее их обоих {ø,{ø}}, создав тем самым {ø,{ø},{ø,{ø}}} и это будет 3. В общем, я думаю принцип понятен, продолжая так делать, мы создадим все возможные натуральные числа. На самом деле в теории множеств, создаваемые таким образом числа именуются ординалами^[110], и натуральные числа являются лишь малой частью этого класса чисел (подробнее о том, что такое ординалы, мы еще поговорим в дальнейшем). Но самое главное в аксиоме бесконечности даже не то что она определяет понятие натурального числа, а то что утверждает, что создаваемые таким образом числа в итоге образуют бесконечное множество: {ø,{ø},{ø,{ø}},{{ø},{ø,{ø}}},...}. Теория создает бесконечность как объект, с которым можно работать, явно заявляя, что бесконечность существует. Но есть еще один важный момент в формулировке аксиомы, который не сразу заметен, она говорит, что существует "по крайней мере одно" бесконечное множество, это значит что можно создать и другие бесконечные множества при чем на основе этого же, делая его, если можно так выразиться, еще более бесконечным. Каким образом можно сделать бесконечность еще больше, мы, так или иначе, будем разбирать на протяжении всей книги, пока следует уяснить, что аксиома бесконечности говорит, что у бесконечности в любом ее проявлении нет конца, а значит и не может существовать никакого множества всех множеств. Так аксиома бесконечности спасла теорию множеств от главного разрушавшего ее противоречия.

Cедьмую и восьмую аксиомы иногда принято называть схемами (так же как аксиомы индукции в арифметике), как мы выяснили, это такой расширяемый вид аксиом, на основе которых можно конструировать теоремы или даже другие аксиомы. Обе они содержат общую основную идею о том, что всякое суждение об элементах множества создает новое множество (возможно тоже самое множество). Из формулировки, правда, не совсем ясно, что такое суждение. Под суждением как раз и подразумеваются всякие корректные математические высказывания (формулы теории множеств), которые можно использовать в формулировке теорем или определении аксиом в том числе и для других разделов математики. Так теория множеств позволяет вывести из собственно множеств почти всевозможные объекты в математике и отношения между ними, поэтому на языке теории множеств можно переформулировать практически любую отрасль математики. Примером выделения множества может быть следующее суждение "два наименьших числа в множестве натуральных чисел", результатом суждения будет конечное множество {0,1}. Примером преобразования множеств может служить другой пример суждения: "умножить каждый элемент множества натуральных чисел на 2", результатом суждения будет бесконечное множество четных чисел {0,2,4,6,8,...}.

Девятая аксиома как следует из определения, утверждает что для каждого множества существует другое множество содержащее множество всех подмножеств первого. Эта аксиома кажется очевидной, например, обсуждая третью аксиому мы перечислили все подмножества множества {a,b,c}; кажется естественным, что из всех его подмножеств можно сделать другое множество: {ø,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}, но это очевидно только для конечных множеств. Когда мы позже попытаемся найти множество всех подмножеств для бесконечного множества, вы удивитесь к каким поразительным последствиям это приведет. Именно благодаря этой аксиоме мы можем вывести из теории множеств иррациональные числа и поля необходимые для математического анализа, а так же все основные геометрические концепции: точки, прямые и плоскости.

Десятую аксиому считают самой спорной, даже из названия системы аксиом (Аксиомы Цермело и Френкеля, плюс Аксиома выбора) следует, что некоторые математики не любят включать ее в список, хотя она и была добавлена изначально самим Цермело. Иногда следствия этой аксиомы кажутся сами собой разумеющимися, и в период когда создавалась аксиоматика теории множеств, по всей видимости авторы посчитали ее чересчур очевидной и безоговорочно и без всяких исключений включили в общий список, но как оказалось позже, в том числе за счет знаменитой теоремы Гёделя о неполноте, если мы не обозначим это утверждение как явное и исключим аксиому выбора из общего списка аксиом, то это приведет нас к абсолютно иным следствиям. Из формулировки аксиомы следует, что для любых непересекающихся множеств должен существовать критерий выбора, по которому мы возьмем по элементу из каждого, при том что аксиома ничего не говорит о самом этом критерии. Интуитивно это можно объяснить так: пусть у нас есть несколько коробок с новыми ботинками, в этом случае критерий выбора установить просто: берем по правому или левому ботинку из каждой коробки; но если перед нами коробки с абсолютно разным хламом, или например только с одинаковыми предметами, аксиома выбора утверждает, что мы все равно можем придумать критерий выбора. Конечно сложно вот так без подготовки полностью понять эту аксиому и суть того, для чего она нужна, поэтому давайте рассмотрим основной вывод, который из нее следует: всякое множество можно упорядочить. То есть какое бы множество мы не взяли, каждому элементу этого множества можно сопоставить порядковое число. Опять же вроде бы очевидное утверждение, уже не кажется таким очевидным, когда речь идет о бесконечных множествах, но все это мы еще будем разбирать в дальнейшем.

Вот так бегло разобрав аксиомы теории множеств, мы готовы изучать бесконечность, ведь такой инструмент как множество позволяет к ней подступится. Итак бесконечность - это множество, вернее бесконечное множество. Если мы представим натуральные числа как конечные множества, то это даст нам возможность работать с числами и бесконечностью одновременно. Первым делом просто констатируем тот факт, что нет смысла сравнивать конечные и бесконечные множества по величине, так как бесконечные всегда будут больше. Значит, простите за очевидность, бесконечность будет больше любого возможного конечного числа. Гугол, гуголплекс, Число Грэма и даже любые придуманные в любых более сильных нотациях числа - все они ничто по сравнению с бесконечностью, ведь к ним всегда можно сделать +1 и снова +1 и так далее. Не существует самого большого числа, из него всегда можно сделать число еще больше. А если к бесконечности прибавить 1, это что-нибудь изменит? Казалось бы, нам не нужно быть выдающимся математиком, чтобы осознать: сколько не прибавляй к бесконечности, она все равно останется бесконечностью, но вот тут выдающиеся математики могут с нами поспорить и сказать, что это не всегда так.

Чтобы понять, чего такого знают эти выдающиеся математики, чего не знаем мы, нам следует разобрать еще одну важную вещь, чем отличается порядок от количества, поскольку это имеет большое значение для бесконечных множеств. Но сперва давайте разберем какое значение порядок имеет для конечных чисел. На самом деле в математике для конечных чисел порядку не уделяется большого значения, чего не скажешь о нашей речи. Почти в каждом языке мира есть количественные и порядковые числительные. Для правильного изъяснения мыслей необходимо разделять по смыслу слова: один и первый, два и второй, три и третий и т.д. Но в математике казалось бы это не имеет смысла, ведь если у нас есть пять яблок, естественно есть и пятое. Да и все арифметические действия одинаково работают как с порядковыми, так и с количественными числами. Ну правда, к примеру, если на одной стороне улицы стоит пять домов, а потом будет построено еще пять - их станет десять; так же как если бы я шел по этой улице и считал дома: досчитав до пятого, а потом пересчитав еще пять следующих за ним, я бы обнаружил десятый дом. И все же несмотря на то, что во многих разделах математики разделение чисел на количественные и порядковые не требуется, для них придуманы названия: порядковые - это ординалы, а количественные - это кардиналы. Запоминайте эти названия, если еще их не знаете, дальше мы будем использовать только их.

С ординалами мы уже встречались это те самые абстрактные числа, которые создаются аксиомой бесконечности из пустого множества. Они создавались нами из пустоты в строго определенном порядке, так что упорядоченность заложена в их природе (поскольку будучи множеством бо́льший ординал обязан содержать в себе все предыдущие). Эти числа и есть номера, которые мы даем всем возможным предметам, когда пытаемся их пересчитать, ну а в соответствии с аксиомой выбора любому элементу любого множества можно присвоить ординал, чтобы упорядочить это множество. Кардиналы имеют смысл только когда есть количество и его можно обхватить и измерить его "количественность" или как более корректно говорят в математике кардинальность множества. В общем основной вывод в том, что для конечных множеств {a,b,c,d,e} ординал множества (порядковый номер последнего элемента) соответствует кардиналу множества (количеству элементов), |5| = 5.

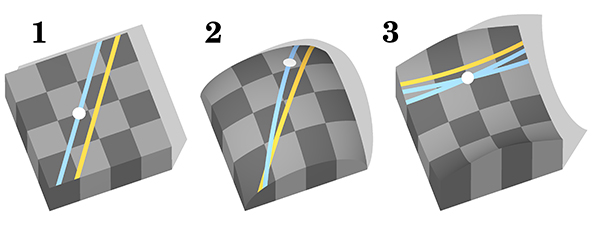
Однако, как я и упоминал, ординалы и кардиналы не отличаются только пока мы говорим о конечных числах. Как только речь заходит о бесконечности, ситуация меняется. Но как вообще порядок можно применить к бесконечности? Когда мы говорим бесконечное количество - это имеет смысл, однако выражение: находящийся под бесконечным номером - кажется нам бессмысленным, но так происходит только если мы говорим об однородной бесконечности. А ведь, бесконечности могут быть неоднородными. Вот вам хрестоматийный пример. Представьте себе бесконечную последовательность вертикальных линий, которая имеет начало, и в которой каждая следующая линия короче предыдущей, так же сокращается и расстояние между ними. Понятно, что в какой-то точке такая последовательность обращается в бесконечность, но наш глаз уже не сможет это разглядеть.

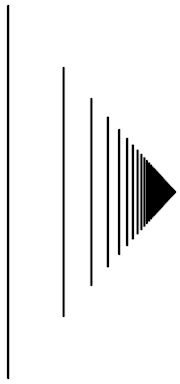
И вопрос - какое по порядку последнее число в этой последовательности - по-прежнему кажется нам бессмысленным, ибо в этой последовательности нет последней линии. Но если мы возьмем вот такой рисунок:

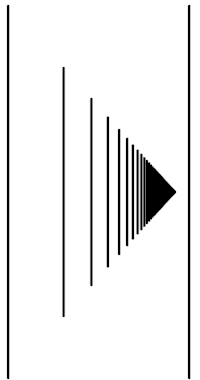
То здесь последняя линия есть. Так какой же у нее порядковый номер? А номер у этой последней линии должен быть, ведь аксиома выбора утверждает, что любое множество можно упорядочить. Ну... получается, что ее порядковый номер это ∞+1. Но разве это имеет смысл, ведь общее количество по-прежнему бесконечно, а если к бесконечному количеству элементов прибавить еще один, их количество все равно будет бесконечным. Вот здесь и начинается расхождение если мы говорим про количество, то ∞+1 = ∞, но если мы говорим о порядке, то ∞+1 ≠ ∞. Значит, начиная с этого момента, ординалы и кардиналы необходимо разделять. Количественную бесконечность выражают в так называемых трансфинитных кардиналах (что в дословном переводе с латинского означает количественное число за пределами бесконечности) и записывают их буквой еврейского алфавита Алеф (ℵ). Когда же речь идет о порядковой бесконечности употребляют выражение: трансфинитные ординалы (что в дословном переводе с латинского означает порядковое число за пределами бесконечности) и записывают буквой греческого алфавита омега (ω). Я предлагаю в дальнейшем опускать слово "трансфинитный", и если мы будем говорить об ординалах или кардиналах, я буду иметь ввиду бесконечные числа. Ну а поскольку конечные числа не имеет смысла разделять на ординалы и кардиналы, то когда о них зайдет речь, так и будем говорить, просто "конечные числа".

С терминологией и записью разобрались, идем дальше. Значит, ∞+1 = ∞ справедливо только для кардиналов, то есть ℵ+1 = ℵ. Ординалы же подчиняются другому правилу: ω+1 > ω, а значит у них иная арифметика. Арифметику кардиналов мы рассмотрим чуть позже, это тоже будет нам необходимо для постижения сверхбольших чисел. Так же я больше не буду использовать символ "∞" в выражениях, поскольку в нем нет ясности о какой именно бесконечности идет речь, о количественной или о порядковой. Но пока вернемся к ординалам. Итак, после всех конечных порядковых чисел идет ω (первый трансфинитный ординал). Так же обратите внимание, что в математике, так же как и в информатике, порядковые числа принято считать с нуля (но на самом деле это большой роли не играет, для чего это необходимо я объясню позже).

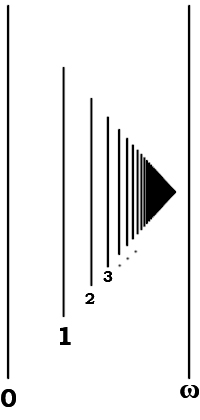
Следующую линию можно обозначить ω+1, затем ω+2 и так далее до ω+ω (или ω×2). Тут стоит оговориться, что ω+1 ≠ 1+ω, то есть знакомый нам со школы закон о перестановке слагаемых с транcфинитными ординалами не работает^[111]. И действительно, посмотрите снова на рисунок и попытайтесь отсчитать бесконечное число раз начиная с линии под номером "1", очевидно же, что до ω+1 вы не досчитаетесь, ибо бесконечность пересчитать невозможно, значит 1+ω = ω.

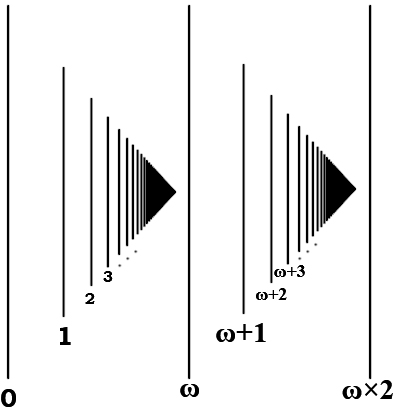
С умножением трансфинитных ординалов происходит тоже что и со сложением, закон перестановок множителей не работает^[111]: 2×ω ≠ ω×2 и 2×ω = ω. В целом, последовательность из умножений ω×2, ω×3 ... закончится на ω×ω (или ω²). Вот так это можно визуализировать:

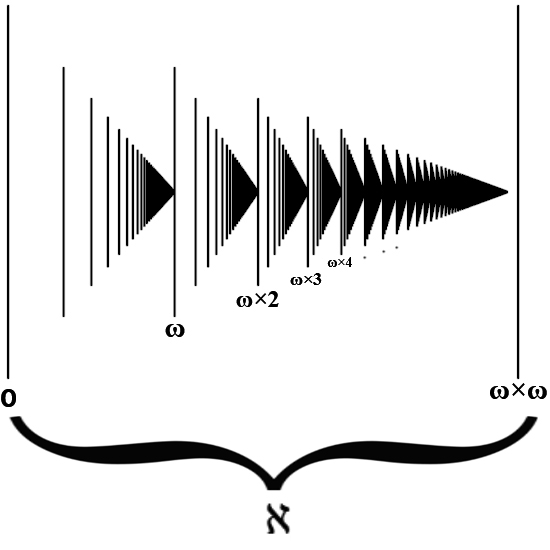
Хочу отметить, что несмотря на то, что мы уже добрались до ω², мы по-прежнему обсуждаем с вами порядок, а не количество. А количество все так же остается равным просто бесконечности (ℵ), как и на предыдущих рисунках. Кроме того, раз мы уже имеем дело со степенью, давайте отметим еще одну особенность ординальной арифметики: 2^ω = n^ω = ω, где n < ω^[111]. Ну а череду степеней также можно продолжить: ω², ω³, ... до ω^ω.

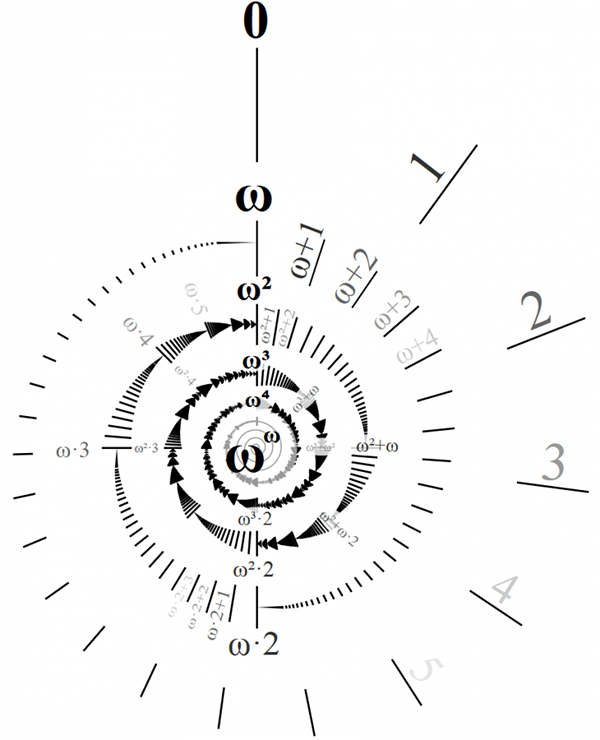
Дальнейшая визуализация этого безумия будет затруднительна, но я думаю принцип вам понятен, неоднородность бесконечности можно увеличивать бесконечно. За ω^ω идет ω^ωω, ω^ωωω, ω^ωωωω, и так далее вплоть до бесконечной степенной башни из ω. Но мы пока не будем городить рекурсии из ординалов, этим мы займемся позже и заниматься будем очень и очень долго, поскольку именно рекурсии ординалов напрямую связаны с построением сверхбольших чисел. На данный момент все что следует уяснить, так это то, что какую бы рекурсию из ординалов мы бы не соорудили, количественная характеристика получившегося ординала по-прежнему будет равна просто бесконечности (ℵ). На рисунках 33, 34, 35 и 36 изображено одинаково бесконечное количество палочек. Количественную характеристику ординалов принято записывать как модуль числа: |ω| = |ω+1| = |ω×2| = |ω²| = |ω^ω| = |ω^ωω| = |ω^ωω...| = ℵ.

Вычитание и целочисленное деление тоже определены на ординалах, однако эти операции не всегда могут изменить исходный ординал^[111]. Например: ω+5-1 = ω+4; ω×3-ω = ω×2; но ω-1 = ω; ω²-ω = ω²; и так же ω×2/ω = 2; ω²/ω = ω; но ω×2/2 = ω×2; ω^ω/ω = ω^ω. Эти примеры станут вам интуитивно понятными, если вы еще раз взгляните на рисунки, и чтобы лучше понимать природу ординалов попробуете самостоятельно разобраться почему данные равенства выполняются.

Все же полезно представлять ординалы не только как палочки, а прежде всего держать в голове, что по определению это упорядоченные множества, каждое из которых содержит в себе все предыдущие множества в качестве элементов. Например: 5 = {0,1,2,3,4}; ω = {0,1,2,3,4,5,...}; ω+1 = {0,1,2,3,4,5,...,ω}; ω×2 = {0,1,2,3,4,5,...,ω,ω+1,ω+2,...}. Такое представление ординалов четко делит их на две категории: очередные (successor) ординалы и предельные (limit) ординалы (ноль - исключение, и не явлется ни тем ни другим)^[112]. Очередными ординалами называют такие, у которых есть последний элемент, например: 5 = {0,1,2,3,4}; ω+1 = {0,1,2,3,4,5,...,ω}; такое название обусловлено тем, что они всегда следуют за каким-то конкретным ординалом (который как раз равен этому последнему элементу), так например, 5 следует за 4, а ω+1 следует за ω, а у предельных ординалов нет конкретного предшественника, перед ними находится бесконечность. Соответственно, поэтому предельные ординалы, будучи множествами, не имеют последнего элемента, например: ω = {0,1,2,3,4,5,...}; ω×2 = {0,1,2,3,4,5,...,ω,ω+1,ω+2,...}. Собственно, не трудно догадаться, что очередные ординалы всегда будут выглядеть как "...+n", где n - натуральное число больше нуля. Эту несложную классификацию ординалов я привожу здесь не просто так, в дальнейшем она очень нам пригодится для создания больших чисел.

Итак трансфинитные ординалы бывают разные, они отличаются по видам и по величине. Но могут ли быть разными трансфинитные кардиналы, могут ли они отличаться по величине. Может ли быть что-либо количественно больше чем ℵ - обычная количественная бесконечность? Оказывается, что количественные бесконечности бывают разной мощности, одна больше другой. Чтобы понять как это так, сначала давайте разберемся с арифметикой трансфинитных кардиналов. Поможет нам в этом задачка придуманная тем самым Давидом Гильбертом, который собирался аксиоматизировать всю математику единой системой аксиом^[113]. По условиям задачи мы имеем отель, в котором бесчисленное множество номеров, и который всегда заполнен, но его девиз в том, что "В нашем отеле всегда есть свободные номера". Вопрос, как заселить в такой отель еще одного человека?

Ответ звучит так: менеджеру нужно объявить по громкой связи, что всем постояльцам необходимо переселиться в следующий по счету номер, и что администрация отеля приносит глубочайшие извинения за неудобства. В итоге все постояльцы все равно останутся с номерами (поскольку в бесконечном количестве номеров нет последнего номера, из которого некуда было бы переселяться), а у нас появится одно свободное место. Вот и получается, что ℵ+1 = ℵ. Если же прибудет сразу два или три новых постояльца, тоже не беда, объявляем по громкой связи, что необходимо всем переселиться через два или три номера соответственно. Значит ℵ+n = ℵ, где n - любое натуральное число.

Даже если в отель попытается заселиться бесконечно много новых постояльцев, менеджер сможет справится с задачей, объявив по громкой связи, что всем прежним постояльцам необходимо переселиться из своего прежнего номера n в номер равный n×2. Тогда постоялец из номера 1 переселится в номер 2, постоялец из номера 2 в номер 4, постоялец из номера 3 в номер 6 и т.д. Это освободит все нечетные номера. В этом и вся прелесть количественной бесконечности, она всегда одинаковая: а значит бесконечное множество четных номеров такое же по величине как и бесконечное множество нечетных, и такое же по величине как и бесконечное множество всех номеров, как бы странно это не звучало. Менеджеру остается только объявить по громкой связи, что все новые постояльцы, которые стоят в очереди за номерами заселяются в номер отеля n×2-1, от номера в порядке той очереди в которой они собрались. Тогда первый стоящий в очереди займет номер 1, второй стоящий в очереди номер 3, третий стоящий в очереди номер 5, и так далее. Всего два объявления по громкой связи и проблема решена. Значит ℵ+ℵ = ℵ. Это так же показывает, что количество целых чисел (всех целых не только положительных, но и отрицательных: ...,-4,-3,-2,-1,0,1,2,3,4,...) столь же бесконечно (ℵ), как и количество натуральных чисел (0,1,2,3,4,...), потому что они сопоставимы. На примере отеля это можно продемонстрировать так: постояльцев, что живут в нашем отеле можно обозначить положительными числами, а новоприбывших отрицательными числами, и как было показано, все они смогут расселится в нашем бесконечном отеле.

А если мы выселим одного постояльца, сколько их останется в гостинице. Конечно, по логике получается, что бесконечное количество. А если двух или трех, то останется тоже бесконечное количество. А если выселим бесконечное количество постояльцев? По идее ℵ-ℵ должен получиться 0 (если, например, мы выселяем всех постояльцев), но если рассмотреть эту ситуацию подробнее, то все оказывается не так просто. Допустим, если мы возьмем постояльцев из четных номеров и выселим их из отеля. Их число будет бесконечным, как собственно и число постояльцев оставшихся в нечетных номерах, следовательно: ℵ-ℵ = ℵ. Множество четных номеров является подмножеством всех номеров, но оба они бесконечны. Так как же решать ℵ-ℵ, ведь если мы выселяем только четные номера, то ℵ-ℵ = ℵ, а если выселяем всех, то ℵ-ℵ = 0. А вот еще возможные варианты: если мы выселим всех кроме первого постояльца, то получится ℵ-ℵ = 1, или если всех кроме первого и второго постояльца, то получим ℵ-ℵ = 2. Получается, что ℵ-ℵ неопределенная операция (кто проходил в старших классах математический анализ и умеет находить пределы элементарных функций, знает, что в ситуации ℵ-ℵ необходимо избавляться от неопределенности). Для этого и нужна аксиома выбора, согласно которой, выполняя операцию ℵ-ℵ в теории множеств, мы обязаны знать, какое именно бесконечное подмножество мы собираемся вычитать из бесконечного множества.

Необходимость соблюдения аксиомы выбора при вычитании бесконечных множеств становится очевидным еще в одной загадке про бесконечность, которая называется "Вредный Дед Мороз"^[114]. В задаче рассказывается про Деда Мороза, который пришел к детишкам, чтобы подарить им конфеты. В мешке у Деда Мороза бесконечное количество конфет. Однако Дед Мороз дает конфеты с тем условием, что заберет половину от того что дал. Казалось бы совершенно очевидно, что сколько бы конфет Дед Мороз не даст детям, они всегда будут в выигрыше. Но если спроецировать эту задачу на бесконечную раздачу конфет все окажется очень странным. Допустим, за час до Нового года Дед Мороз выдал две конфеты, под номером 1 и 2, и сразу забрал конфету под номером 1 (осталась конфета под номером 2). За полчаса до Нового года Дед Мороз выдал четыре конфеты, под номерами 3, 4, 5, 6 и забрал две конфеты под номерами 2 и 3 (остались конфеты с номерами 4, 5, 6). За четверть часа до Нового года Дед Мороз выдал шесть конфет, под номерами 7, 8, 9, 10, 11, 12 и забрал три конфеты под номерами 4, 5, 6 (остались конфеты с номерами 7, 8, 9, 10, 11, 12). За восемь минут до Нового года Дед Мороз выдал восемь конфет, под номерами 13, 14, 15, 16, 17, 18, 19, 20 и забрал четыре конфеты под номерами 7, 8, 9, 10 (остались конфеты с номерами 11, 12, 13, 14, 15, 16, 17, 18, 19, 20). И так далее, основной принцип я думаю всем уже понятен, Дед Мороз дает все больше и больше конфет за все более сокращающиеся промежутки времени. Вроде бы до сих пор никакого противоречия не возникло, число конфет у детей стабильно растет. Вопрос в задаче ставится следующим образом, сколько конфет будет у детей в полночь. Если по мере того как время приближается к новому году Дед Мороз дает конфеты все чаще и чаще, значит когда Новый год наступит число конфет у детей станет бесконечным. Но сколько же тогда конфет заберет Дед Мороз, получается, что тоже бесконечное количество, а поскольку у нас не было никакого критерия выбора конфет Дедом Морозом, значит он забрал все бесконечное количество конфет и у детей не осталось ничего. Значит без аксиомы выбора и правильно заданного критерия в данной задаче мы получим ℵ-ℵ = 0.

Если бы среди детей был хотя бы один ребенок, увлекающийся математикой он бы сразу раскусил хитрого Деда Мороза и попросил бы Деда Мороза забирать конфеты только под нечетными номерами. Тогда в первый раз Дед Мороз дал бы конфеты 1 и 2, а забрал бы по-прежнему 1ую (осталась 2ая). Второй раз дал бы конфеты: 3, 4, 5, 6 и забрал бы 3 и 5 (остались 2, 4, 6). В третий раз дал бы конфеты 7, 8, 9, 10, 11, 12, а забрал бы 7, 9, 11 (остались 2, 4, 6, 8, 10, 12). В четвертый дал бы конфеты 13, 14, 15, 16, 17, 18, 19, 20, а забрал бы 13, 15, 17, 19 (остались 2, 4, 6, 8, 10, 12, 14, 16, 18, 20). Теперь все ясно, к моменту наступления Нового года у детей будет бесконечное количество конфет с четными номерами, а Дед Мороз заберет бесконечное количество конфет с нечетными номерами. Соблюдая аксиому выбора мы опять получили ℵ-ℵ = ℵ, так же как и с выселением постояльцев из четных номеров бесконечного отеля.

Умножение не сильно изменит ситуацию в арифметике бесконечных кардиналов: ℵ×n = ℵ, где n - любое натуральное число. Ведь в сущности уже ℵ+ℵ = ℵ эквивалентно ℵ×2 = ℵ. Легко наглядно, на примере отеля показать, что и ℵ×3 = ℵ, например приехало к нам заселяться два автобуса новых постояльцев в каждом бесконечное количество пассажиров. Менеджер так же объявляет по громкой связи, что прежним постояльцам необходимо переселиться, но уже в номера равные n×3, где n - номер в котором проживает постоялец (тогда занятыми окажутся третий, шестой, девятый и т.д., кратные трем номера). Пассажирам первого автобуса необходимо объявить, что они должны заселяются в номера отеля n×3-1 (второй номер, пятый номер, восьмой номер и т.д.), а пассажиры второго автобуса заселяются в номера отеля n×3-2 (первый номер, четвертый номер, седьмой номер и т.д.).

Деление тоже легко выполнять: ℵ/n = ℵ, при условии, что мы будем использовать аксиому выбора и уточнять о каких подмножествах идет речь. Наши действия с выселением из четных номеров это все равно, что разделить бесконечность на два: ℵ/2 = ℵ. Но чтобы проще понимать деление на бесконечных множествах, давайте себе представим пустой отель, в который заселяется бесконечное множество постояльцев, каждый из которых требует выделить ему по два номера. Аналогично менеджер должен объявить, что каждый стоящий в очереди берет себе номера n×2 и n×2-1, где n - номер за которым он стоит в очереди. Если постояльцы потребуют по три номера на человека, тогда пусть каждый берет номера n×3, n×3-1 и n×3-2, что доказывает: ℵ/3 = ℵ. Если постояльцы запросят больше номеров на человека, менеджер сможет дать им и больше, хоть по 100, хоть по гугол номеров на человека, все равно в результате такого расточительства гостиничной собственности все постояльцы будут заселены, ведь как и заявлено в девизе "в отеле всегда есть свободные номера", и можно было бы еще приписать "...даже если вы захотите занять сразу несколько". Вот и получается, что ℵ/n = ℵ, где n - любое натуральное число и соблюдается аксиома выбора.

Однако ситуация с выражениями ℵ×ℵ и  ℵ/ℵ оказывается посложнее. Представим, что бесконечная вереница автобусов прибывает к стойке регистрации. Если менеджер попытается провести свой трюк с удвоением (переселением всех постояльцев из в номеров n в номера n×2), то это даст возможность заселить только один автобус. Если сделать утроение (переселить всех постояльцев из в номеров n в номера n×3), то сможет расселить два автобуса, как он это уже делал. Но как справится с бесконечным количеством автобусов. Тут надо прибегнуть к совершенно иной схеме расселения.

Прежде всего давайте представим, что мы расселяем бесконечное количество пассажиров из бесконечного числа автобусов в пустой отель с бесконечным количеством номеров. Мы конечно можем работать и с полным отелем, освободив по вышеуказанной схеме все четные места, что так же даст нам бесконечное количество номеров в отеле, но раз это равносильно, то давайте упростим условия, сохранив основной принцип задачи.

Чтобы понять, как решить задачу, нам следует визуализировать всех людей, которых должен поселить менеджер. Конечно, он не может составить список из буквально всех людей, так как в этом случае диаграмма должна быть бесконечной в обоих направлениях. Но окончательный вариант картинки будет соответствующим:

Если включить в таблицу достаточное количество строк и столбцов, то каждый пассажир будет учтен. За каждым пассажиром закреплен уникальный идентификатор, состоящий из номера сидения и номера автобуса. Если менеджер будет работать отдельно с каждым автобусом, то получается что он будет создавать очередь из заселяющихся, которая на диаграмме расположена вдоль первой строки и тогда сможет расселить лишь один автобус.

Конечно он может создать несколько параллельных очередей, объявив по громкой связи правила заселения для каждого автобуса (например, пассажиры первого автобуса заселяются в номера n×4, второго в номера n×4-1, третьего в номера n×4-2, четвертого в номера n×4-3 - это позволит расселить сразу четыре автобуса). Но для создания таких параллельных очередей ему заранее надо знать какое конкретное количество автобусов он расселяет, иначе он не сможет подобрать кратность расселения поселенцев по комнатам.

Очевидно, что надо разработать схему, которая позволяла бы работать сразу со всеми автобусами. Такая схема называется диагонализация^[115]. Вместо движения вдоль первой строки (обслуживая только первый автобус) необходимо двигаться из угла по зигзагообразной схеме, как показано ниже:

1ому пассажиру 1ого автобуса достанется 1ый номер. 2ому пассажиру 1ого автобуса и 1ому пассажиру 2ого автобуса достанутся 2ой и 3ий номера соответственно. После чего берем поселенцев из третей диагонали: 1ого пассажира 3его автобуса, 2ого пассажира 2ого автобуса и 1ого пассажира 3его автобуса и даем им 4ый, 5ый, 6ой номера соответственно. Затем переходим к следующей диагонали и так далее. Таким образом на нашей диаграмме рисуется треугольник все больших и больших размеров. Однако если менеджер будет каждого так расселять по такому диагональному методу у него уйдет на это целая вечность. Значит он должен воспользоваться громкой связью и объявить пассажирам какие номера они должны занять самостоятельно. Формула заселения для каждого пассажира будет звучать следующим образом: N = (a+b-2)×(a+b-1)/2+b, где a - номер сидения, b - номер автобуса, N - номер, куда мы его поселим.

Наша способность расселить в нашем бесконечном отеле бесконечную череду автобусов с бесконечным числом пассажиров в каждом, доказывает что ℵ×ℵ = ℵ. Аналогично, если мы будем пользоваться вышеприведенной формулой (которая является критерием выбора), но в обратном порядке, то можем выселить этих постояльцев и расселить их обратно по бесконечной череде автобусов, так чтобы в каждом было бесконечное число пассажиров, значит и ℵ/ℵ = ℵ (если аксиома выбора соблюдена). Но если мы не задаем критерий выбора, то можем сказать поселенцам при выселении: "садитесь в автобусы по 10 человек в каждый, или по 20  человек каждый". Это уже не критерий выбора, а критерий распределения, тогда опять же не соблюдается аксиома выбора и получается неопределенность, поскольку и в первом (ℵ/ℵ = 10) и во втором случае (ℵ/ℵ = 20) все постояльцы рассядутся по автобусам, ведь тех бесконечное количество, так же как и постояльцев. В старших классах при решении задач по нахождению пределов, сталкиваясь с ситуацией ℵ/ℵ так же приходится избавляться от неопределенности, потому что в математическом анализе при нахождении предела не задается критерий выбора.

А еще это доказывает, что все множество дробных чисел, настолько же бесконечно, как и множество натуральных чисел, то есть их количественные характеристики равны. Хотя на первый взгляд кажется, что дробей больше, ведь только между 0 и 1 их можно уместить бесконечное множество (1/2, 1/4, 1/8, 1/16 и т.д.). Но раз ℵ/ℵ = ℵ, значит и любой дроби можно сопоставить натуральное число. Для пущей убедительности можно расписать дроби в диаграмму так же как мы сделали с пассажирами, только вместо номера сидения пишем числитель дроби (a), а вместо номера автобуса пишем знаменатель (b) и так же при помощи диагонализации бесконечно перечисляем все дроби (a/b).

Выражение ℵ×ℵ = ℵ равносильно выражению ℵ² = ℵ, логично предположить, что справедливы и ℵ³ = ℵ, и ℵ⁴ = ℵ, и ℵⁿ = ℵ. Давайте проверим, сможем ли мы показать так ли это на примере нашего отеля. ℵ³ можно представить так: к отелю пребывает бесконечное количество поездов в каждом поезде бесконечное количество вагонов, в каждом вагоне бесконечное количество пассажиров. Как же будет расселять их менеджер? Ему потребуется уже трехмерная диаграмма в которой по одной оси отложены места в вагоне, по второй номера вагонов, а по третей номера поездов. Однако и здесь можно применить диагонализацию, только в процессе диагонализации будет создаваться не растущий треугольник, а растущая пирамида (ведь диаграмма то трехмерная). Формула расселения пассажиров, которую должен объявить менеджер станет немного сложнее: N = (a+b+с-3)×(a+b+с-2)×(a+b+с-1)/6+(b+с-2)×(b+с-1)/2+с, где a - номер сидения, b - номер вагона, с - номер поезда, N - номер, куда мы его поселим.

Усложняем задачу до уровня ℵ⁴. К отелю подплывает бесконечное количество паромов в каждом из которых бесконечное количество поездов, в каждом поезде бесконечное количество вагонов и в каждом вагоне бесконечное количество пассажиров. Не сложно догадаться, что диаграмму необходимо делать четырехмерной, и делать диагонализацию в виде растущей четырехмерной пирамиды. Понятно, что менеджеру не просто будет такое визуализировать, но если он знает общий принцип, то легко сможет вывести формулу расселения, которую опять же объявит по громкой связи. А формула, становится все сложнее и сложнее:  N = (a+b+с+d-4)×(a+b+с+d-3)×(a+b+с+d-2)×(a+b+с+d-1)/24+(b+с+d-3)×(b+с+d-2)×(b+с+d-1)/6+(с+d-2)×(с+d-1)/2+d, где a - номер сидения, b - номер вагона, с - номер поезда, d - номер парома, N - номер в отеле, куда мы его поселим. Конечно теперь менеджеру только останется надеяться, что пассажиры достаточно подкованы в математике, чтобы подставить числа и рассчитать в какую же комнату им необходимо расселиться.

Такой общий принцип расселения называется в математике симплексным распределением или методом многомерных треугольных чисел^[5]. В таблицах №10, №11 и №12 приведены образцы порядка расселения постояльцев для ℵ², ℵ³ и ℵ⁴ соответственно. А тем, кто обладает немного более продвинутыми знаниями, будет интересна общая формула симплексного распределения на рисунке №40.

Не стоит вдаваться в суть формулы, ее понимание не имеет отношения к сути повествования, главное что стоит вынести из этого, так это то, что мы можем применять формулу симплексного разложения, чтобы разложить любую конечную вложенность бесконечностей в обычную бесконечность натуральных чисел, а значит ℵⁿ = ℵ, где n - любое натуральное число. Здесь стоит отметить, что и обратный процесс так же возможен, ведь по сути формула симплексного разложения является критерием выбора, а значит в соответствии с аксиомой выбора: √ℵ = ℵ, ³√ℵ = ℵ, ⁴√ℵ = ℵ, и т.д., ⁿ√ℵ = ℵ.

Более того симплексное разложение не единственный способ разложения вложенных бесконечностей. Мы можем распределять все эти вложенные бесконечные колонны, заселяя их пассажиров, так что в отеле еще останутся свободные номера. Один из таких методов называется факторизацией простых чисел^[116]. Да и формула у него попроще, пассажирам будет проще посчитать в какой номер им заселяться. Итак, если постояльцы приехали в бесконечном количестве автобусов, по бесконечному количеству пассажиров в каждом (ℵ сидений × ℵ автобусов), менеджеру необходимо объявить формулу: N = 2^a×3^b, где a - номер сидения, b - номер автобуса, N - номер в отеле, куда мы его поселим. Если мы имеем тройной уровень вложения (ℵ сидений × ℵ вагонов × ℵ поездов), тогда формула будет выглядеть так: N = 2^a×3^b×5^с, где a - номер сидения, b - номер вагона, c - номер поезда, N - номер в отеле, куда мы его поселим. Если четверной уровень вложения (ℵ сидений × ℵ вагонов × ℵ поездов × ℵ паромов), то так N = 2^a×3^b×5^с×7^d, где a - номер сидения, b - номер вагона, c - номер поезда, d - номер поезда, N - номер в отеле, куда мы его поселим. Продолжать в таком духе несложно, увеличивая уровень вложения бесконечностей, мы просто берем следующее простое число и подставляем в формулу. Напомню для тех, кто совсем забыл школьную программу, что простым числом называется число, которое без остатка делится только на само себя или на единицу, других делителей у него нет. В таблицах №13, №14 и №15 приведены образцы порядка расселения постояльцев для ℵ², ℵ³ и ℵ⁴ соответственно методом факторизации простых чисел. Как нетрудно заметить из этих таблиц, в результате такого расселения у постояльцев не будут совпадать номера и у нас останется множество свободных мест (бесконечное множество), причем чем больше уровень вложения, тем реже заселятся пассажиры в отель (хотя количество свободных мест будет по-прежнему просто бесконечным). Так же привожу общую формулу разложения по методу факторизации простых чисел, для тех, кому она будет интересна на рисунке №41. Еще обратите внимание, что в данных таблицах числа номеров отеля не повторяются, то есть для распределения по двум уровням вложенности мы используем одни номера, для распределения по трем уровням вложенности другие номера, и т.д. То есть, если к нам прибудут бесконечные пассажиры сгруппированные по разным уровням вложенности (например, приедет отдельно паром, отдельно поезд, и отдельно автобус), то мы все равно сможем всех расселить. Это значит, что метод факторизации простых чисел расширяемый, и это его свойство пригодится нам в дальнейшем. Симплексное распределение, в свою очередь, не является расширяемым методом, что естественно, ведь этот метод не оставляет пустых мест в отеле, и при иных уровнях вложенности всех придется переселять заново, а значит с его помощью мы не сможем одновременно заселить группы пассажиров, прибывших к нам в разных уровнях вложенности.

Но одно дело расселить всех этих пассажиров, другое дело пересчитать. Представим, что именно такую задачу получил менеджер нашего отеля. Тогда ему просто необходимо знать про трансфинитные ординалы, порядковые бесконечные числа, с которыми мы уже познакомились когда упорядочивали последовательности из бесконечно убывающих палочек. А еще не мешало бы вспомнить основное следствие аксиомы выбора, о том что любое бесконечное множество можно упорядочить. Значит и во всех ситуациях, в которых мы сталкивались с бесконечными множествами состоящих из потенциальных постояльцев отеля, всю совокупность этих множеств, пока мы их еще не расселили, тоже можно упорядочить. Только давайте сразу договоримся, что считать мы всех будем с нуля, так как это любят делать программисты, первый станет нулевым, второй станет первым. Большой разницы вроде бы нет, но как вы увидите, так будет намного удобнее. Итак начнем с ситуации когда у нас полностью заполненный отель и к нам приходит еще один постоялец, и нам надо дать ему номер пока мы его еще не заселили. Поскольку все конечные порядковые номера у нас уже заняты, значит новый постоялец будет постояльцем под номером ω. Если придут сразу два постояльца им можно дать номера ω и ω+1, третий получит номер ω+2 и так далее. Думаю общий смысл понятен, если придет бесконечное количество новых постояльцев всем хватит порядковых номеров, это будут ординалы ω+n. А если приедет автобус с бесконечным количеством постояльцев и еще один придет пешком, то какой порядковый номер будет у него. Ну раз все номера ω+n займут пассажиры автобуса, значит тот кто пришел пешком получит номер ω+ω = ω×2. Ну а если приедет два автобуса с бесконечными количеством пассажиров каждый, то все пассажиры первого автобуса получат номера ω+n, а второго автобуса ω×2+n, ну а если вдруг вместе с ними еще появится один пеший заселяющихся, то мы всегда можем дать ему номер ω×3. Интересная получается ситуация, ординал, который упорядочивает бесконечное множество лежит за пределами этого множества, запомните этот важный момент.

Теперь давайте ненадолго забудем про отель и будем упорядочивать только пассажиров автобусов. Я думаю, вооружившись трансфинитными ординалами, мы с легкостью справимся и с бесконечной вереницей автобусов. Пассажиры первого автобуса получают номера n, второго автобуса ω+n, третьего автобуса ω×2+n, и так далее ω×k+n, где k - номер автобуса, а n - номер сидения. А теперь внимание, вот почему нам необходимо было всех нумеровать начиная с нуля. Пассажир №0 (ω×0+0) сидит на первом (условно нулевом) сидении, первого (условно нулевого) автобуса. Пассажир №1 (ω×0+1) сидит на втором (условно первом) сидении, первого (условно нулевого) автобуса. Пассажир №ω (ω×1+0) сидит на первом (условно нулевом) сидении, второго (условно первого) автобуса. Пассажир №ω+1 (ω×1+1) сидит на втором (условно первом) сидении, второго (условно первого) автобуса. Таким образом, все пассажиры учтены и все ординалы задействованы. И заметьте, у нас опять бесконечность, описываемая двумя числами, то есть бесконечность в квадрате: |ω²| = ℵ² = ℵ. Но чтобы упорядочить всю эту бесконечность, как я и говорил, нам нужен еще один пеший пассажир не входящий в число пассажиров автобуса, его номер и будет ω². На будущее, раз нам всегда нужен кто-то за пределами бесконечного множества, чтобы это множество упорядочить, будем подразумевать что таковой у нас имеется, значит бесконечность постояльцев отеля упорядочивается ω, бесконечность двух автобусов с бесконечным числом пассажиров упорядочивается ω×2, трех автобусов: ω×3, и так далее, бесконечного числа автобусов: ω×ω = ω².

Абстрагируясь от бесконечных постояльцев, мы таким же образом можем пересчитать все целые числа (которые включат в себя как положительные так и отрицательные). Так положительные числа пусть имеют тот номер, который обозначают, а вот числу "-1" присвоим номер ω, числу "-2" присвоим номер ω+1, числу "-3" присвоим номер ω+2, и так далее. В итоге получим, что все целые числа имеют упорядоченность равную ω×2. Ну и как мы уже говорили, ситуацию с бесконечными автобусами можно сопоставить со всевозможными дробными числами, значит и пересчитать дробные числа можно подобным образом. Пусть "1/1" - 1ое дробное число, "1/2" - 2ое дробное число, "1/3" - 3ье дробное число,... и так далее, тогда "2/1" - дробное число под номером ω, "2/2" - дробное число под номером ω+1, "2/3" - дробное число под номером ω+2,... и так далее, ну и аналогично "3/1" - дробное число под номером ω×2, "3/2" - дробное число под номером ω×2+1, "3/3" - дробное число под номером ω×2+2,... В общем я думаю общий принцип понятен так можно продолжать бесконечно в соответствие с таблицей №9, и получится что все дробные числа имеют упорядоченность равную ω². Конечно пытливый ум может заметить, что среди пересчитываемых нами дробных чисел могут попасться и целые числа и сокращаемые дроби (которые могут означать одно и тоже), но на общую упорядоченность это влияние не оказывает, так как, например, не имеет смысла пропускать сокращаемые дроби, потому что все пропуски в пределе счета до бесконечности не имеют смысла ведь мы все равно получим бесконечность. Ну а что касается отрицательных дробей, то с их включением результат тоже не изменится, потому что мы можем чередовать дроби при подсчете (положительная, отрицательная, положительная, отрицательная, и т.д.), все равно в пределе счета до бесконечности все будут учтены. Кроме того общая доля сокращаемых дробей составляет почти 40% (1-6/π², если быть точным, в соответствии с дзета-функцией Римана), так что другой вариант учета отрицательных дробей, это считать их вместо сокращаемых.

Все вышеперечисленные бесконечные множества принято называть счетными. По определению счетным называется такое множество, которое можно один к одному сопоставить с натуральными числами. Отель Гильберта как раз символизирует в данном случае натуральные числа, а расселение всех этих бесконечных пассажиров и есть сопоставление один к одному. Получается, что множества всех натуральных, целых и дробных чисел - счетные. А как мы с вами выяснили, количественно все бесконечные счетные множества равны ℵ, но вот мера их упорядоченности может быть разной, для натуральных чисел это ω, для целых это ω×2, а для дробей ω². То что мы с вами делаем, упорядочивая все возрастающую по неоднородности счетную бесконечность, называется трансфинитной индукцией. Упорядочивание бесконечных счетных множеств всегда происходит путем создания функции, которая создает соотвествие их неоднородной бесконечности с множеством натуральных чисел (расселяет неравномерно распределенных бесконечных постояльцев в наш отель). Следовательно такое упорядочивание бесконечных множеств всегда сопоставимо с рекурсивным выделением подмножеств натуральных чисел. Любая быстрорастущая функция определенная на натуральных числах (будь то тетрация, гипероператор или что-то еще более быстрорастущее), образует некое подмножество натуральных чисел и чем оно разряженее (то есть числа в нем быстро набирают масштаб), тем больше таких подмножеств можно создать, и тогда можно будет "заселить в отель" все бо́льшую неоднородность бесконечности (бо́льший трансфинитный ординал). Получается, что рекурсии для создания больших чисел всегда будут соотвествовать методам выделения подмножеств натуральных чисел, которые можно упорядочить трансфинитными ординалами. Иными словами, чем больше ординал, тем бо́льшую рекурсию на натуральных числах он позволяет создать.

Поразительный вывод, к которому пришел Гедель, заключается в том, что какую бы математическую теорию мы не создали, какую систему аксиом бы мы не выбрали, если она включает в себя арифметику, то всевозможные рекурсии, которые в принципе можно создать в теории всегда будут ограничены размером некого ординала упорядочивающего все счетные подмножества натуральных чисел, которые только может создать теория, а создание этого ординала всегда будет лежать за пределами возможностей этой теории. Существование такого ординала в соответствии с Теоремой Геделя о неполноте доказывает, что теория непротиворечива, ну а величина этого ординала позволяет измерить "силу" теории, то как много абстрактных вещей теория способна сконструировать, какие помножества натуральных чисел выделить и, самое для нас главное, какие рекурсии на них может создать. В русском языке нет устоявшегося термина, но по английски его называют так: Proof-Theoretic Ordinal (PTO), что примерно переводится как теоретико-доказательственный ординал. Нахождение таких ординалов и есть предмет изучения ординального анализа, и получатеся, что именно от величины этого ординала напрямую зависит насколько большие числа можно создать на основе той или иной математической теории^[117].

Но вернемся к упорядочиванию бесконечного транспорта, на очереди ω³. Бесконечное количество поездов с бесконечными вагонами, с бесконечными пассажирами в каждом - можно упорядочить так ω²×m+ω×k+n, где m - номер поезда, k - номер вагона, n - номер сидения. Например, пассажир под номером ω²×2+ω×3+5 сидит на сидении №5, в вагоне №3, в поезде №2. И у нас получилась уже бесконечность описываемая тремя числами, то есть бесконечность в кубе: |ω³| = ℵ³ = ℵ. Не находите, что формула походит на квадратное уравнение, это неспроста, ведь трансфинитные ординалы позволяют измерить не только арифметику, но и алгебру. Бесконечные паромы перевозящие бесконечное количество поездов каждый упорядочиваются уже ω⁴ и формула будет выглядеть так ω³×l+ω²×m+ω×k+n, куда добавился еще l - номер парома (теперь формула похожа на кубическое уравнение, дальше это сходство с алгебраическими выражениями нам пригодится). И так далее, можем продолжать упорядочивать, увеличивая уровень вложенности, но не забываем, что количественно число пассажиров будет оставаться равным ℵ, просто бесконечности.

Можно ли хоть что-то сделать с количественной бесконечностью (ℵ), чтобы увеличить ее в размерах. Ну или что равносильно вопросу, можно ли создать такой поток постояльцев, который бы не смог вместить в себя наш бесконечный отель. На самом деле можно. Представим себе, что про наш отель стало известно всем инопланетянам во всей бесконечной вселенной, и бесконечное количество этих инопланетян сгруппировалось и направилось на землю, но не для того чтобы ее захватить, а чтобы провести отпуск в нашем отеле. А теперь, самое важное, именно, то как они сгрупировались: на каждом космическом корабле находится бесконечное количество пассажиров, корабли объедены в звенья, в каждом звене бесконечное количество кораблей, звенья входят в состав эскадры, в одной эскадре бесконечное количество звеньев, эскадры входят в состав флотилии, в одной флотилии бесконечное количество эскадр, флотилии входят в состав армады, в одной армаде бесконечное количество флотилий, и так до бесконечности. Иными словами вся эта иерархия имеет бесконечный уровень вложенности, что эквивалентно ℵ^ℵ. И вот все они отправляются на землю, чтобы поселиться в нашем отеле. Но к сожалению наш отель в данном случае не оправдает возложенных на него надежд и не сможет разместить у себя всех инопланетных гостей. Администрация отеля не нашла способ расселить все это количество постояльцев и предложила им перегруппироваться. Однако, все что смогли сделать командиры этих кораблей и подразделений, так это уменьшить число пассажиров на каждом корабле до двух, и сделать так, чтобы в звене было лишь два корабля, в эскадре лишь два звена, в флотилии лишь две эскадры, в армаде лишь две флотилии, и так далее до бесконечности, что эквивалентно 2^ℵ. Но и тут произошел казус, оказывается, что даже в этом случае не существует формулы, по которой можно было бы расселить всех постояльцев. Давайте разбираться, почему же наш отель не справляется, когда дело доходит до бесконечной вложенности.

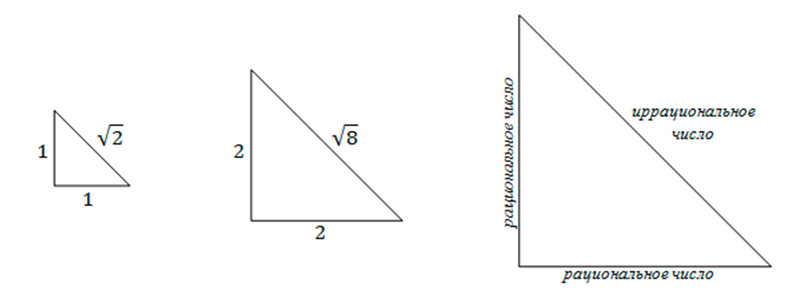
Для начала вспомним, чем рациональные числа отличаются от иррациональных. Знаменитая теорема Пифагора, говорит, что если катеты прямоугольного треугольника равны 1, то его гипотенуза будет равна квадратному корню из двух. Понятно, что √2 это нецелое число. Но оно удивительно тем, что не существует дроби, в виде которой можно его представить, поскольку иначе числитель и знаменатель этой дроби должны быть бесконечными. В десятичной записи √2 ≈ 1,414213562373095048801688724209... и так до бесконечности, причем в последовательности цифр после запятой нет никакой закономерности. В математике встречаются дроби, которые нельзя точно выразить в десятичном виде, например 1/3 ≈ 0,333333333333333333... или 1/7 ≈ 0,142857142857142857..., но все они во-первых могут быть выражены в виде обычной дроби, а во-вторых даже в своем бесконечном десятичном виде имеют периодически повторяющиеся наборы цифр.

По легенде считается, что Пифагор приказал своим последователям утопить собственного ученика Гиппаса, который пришел к такому выводу^[118]. Естественно и Пифагор и Гиппас понимали, что √2 будет нецелым числом, но поначалу Пифагору и в голову не приходило, что √2 невозможно записать дробью. Он считал, что должна существовать какая-то большая дробь, которая будет равна √2. Пифагор предложил способ как это выяснить, используя метод увеличения катетов. Однако если увеличить катеты до 2, то гипотенуза будет равна √8, что тоже не является целым числом, и если мы увеличим катеты до 3, то гипотенуза, ставшая √18, все равно не будет целым числом. Но Пифагор думал, что увеличивая величину катетов, он рано или поздно получит целое число гипотенузы и докажет, что √2 можно записать дробью. Он был полностью обескуражен, когда понял, что в своем эксперименте целого числа он не получит никогда, сколько бы он не увеличивал стороны катетов. Гиппас доказал это от обратного, пусть √2 это дробь a/b, тогда 2 = a²/b² и значит b² = a²/2, но не существует квадратов с целыми сторонами, которые бы по площади отличались ровно в два раза, и Пифагору это было известно.

Для Пифагора это был особенный удар, потому что он верил, что в основе нашего мира лежат целые числа, и что любое явление может быть составлено из отдельных единиц. Это было основой его философского учения о мире, возможно поэтому он так жестоко обошелся с Гиппасом. Даже дроби представлялись ему не как числа, а лишь как пропорции этих чисел. Но из доказательства Гиппаса следовал вывод, что невозможно составить гипотенузу равностороннего прямоугольного треугольника из тех же единиц, из которых составлены катеты, не существует такой пропорции, и значит в мире существуют числа, не поддающиеся рациональному восприятию. Опять же по легенде раскрытие этой тайны среди последователей Пифагора каралось смертью, ибо полностью разрушало их философию.

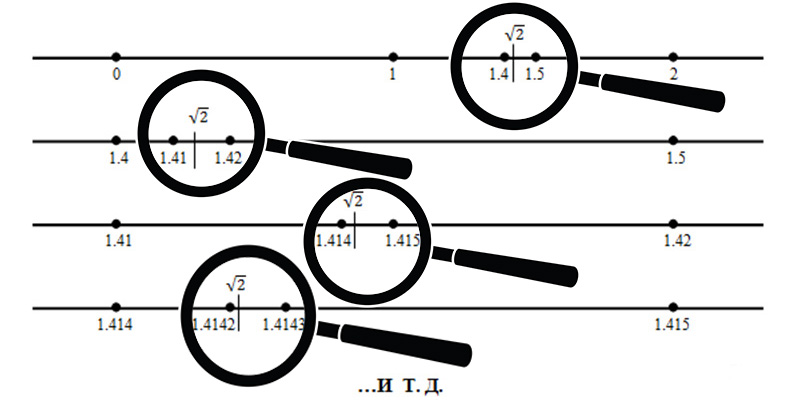
Но какое это отношение имеет к бесконечности? Самое прямое! Когда мы, например, делим бесконечную линию на отрезки, то получаем бесконечность отрезков, которые можно считать. Естественно, если мы попытается их сосчитать, то нам не встретится отрезка под номером √2. Однако если разбить бесконечную линию на безразмерные точки, то где-то на линии можно поставить точку равную отметке в √2. Как это сделать? Очень просто. Берем наш равносторонний прямоугольный треугольник прикладываем его сначала катетом, отмечаем точку 1, затем прикладываем гипотенузой и получаем точку √2. Но проблема в том, что используя традиционное математическое деление получить эту точку невозможно. Значит, сколь малые дробные числа мы бы себе не представили, где-то между ними всегда будут находиться иррациональные числа.

А это значит, что бесконечность иррациональных чисел больше бесконечности натуральных чисел, потому их нельзя сопоставить, что я покажу позже на примере нашего бесконечного отеля. Но пока я хотел бы уточнить, что неизвлекаемые корни это только малая часть иррациональных чисел, и их то как раз можно сопоставить с натуральными. Сделать это несложно, главное вспомнить алгебру. Итак всевозможные рациональные числа, то есть, те которые можно представить в виде дроби x/y являются решением возможных линейных уравнений ax+b = 0, где a и b целые числа. Всевозможные неизвлекаемые квадратные корни или числа их содержащие (например 3+√5, или 2×√3) являются решением возможных квадратных уравнений ax²+bx+c = 0, где a, b и c целые числа. Всевозможные неизвлекаемые кубические корни или числа их содержащие (например √2+³√5, или 4׳√(6+√7)) являются решением возможных кубических уравнений ax³+bx²+cx+d = 0, где a, b, c и d целые числа. И так далее. А теперь давайте вспомним как мы расселяли бесконечных пассажиров (a) из бесконечных автобусов (b), что было эквивалентно бесконечности рациональных чисел или чисел получаемых в уравнениях ax+b = 0. Получается, что расселение бесконечных пассажиров (a) из бесконечных вагонов (b) бесконечных поездов (с) эквивалентно бесконечности чисел получаемых в уравнениях ax²+bx+c = 0. Ну а расселение бесконечных пассажиров (a) из бесконечных вагонов (b) бесконечных поездов (с) бесконечных паромов (d) эквивалентно бесконечности чисел получаемых в уравнениях ax³+bx²+cx+d = 0. Что доказывает, что все возможные неизвлекаемые корни можно сопоставить с натуральными числами и заселить в наш отель. Такие числа, которые могут быть решением степенного уравнения, называются алгебраическими, хоть они и иррациональны, но вся их совокупность так же бесконечна (ℵ), как и бесконечность натуральных чисел (ℵ). Здесь стоит оговориться, что согласно теореме Абеля^[119], начиная с уравнений пятой степени, мы можем столкнуться с такими решениями этих уравнений, которые даже в виде неизвлекаемых корней записать не получится, тем не менее эти числа все равно будут считаться алгебраическими, ведь по определению, являются решениями степенного уравнения, и следовательно их совокупность так же будет счетной.

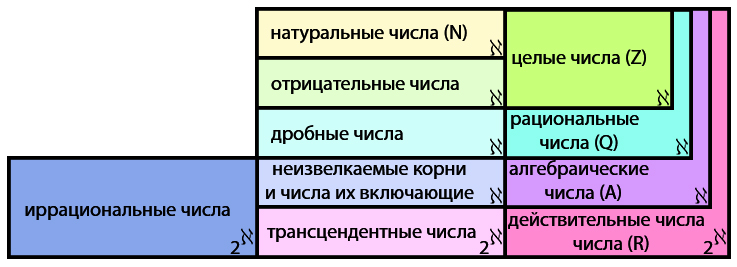
Однако есть такие иррациональные числа, которые не являются алгебраическими, например число Пи. Напомню, что π ≈ 3,14141592653589793238462643383279... - это отношение длины окружности к ее диаметру. Это число не может быть решением никакого степенного уравнения, а значит его нельзя выразить в виде неизвлекаемого корня или числа содержащего неизвекаемый корень. То есть не может быть конечной записи этого числа из обычных натуральных чисел, даже если мы будем пользоваться корнями. Остается только запись в виде бесконечной десятичной дроби с хаотической последовательностей цифр. Такие числа называют трансцендентными, что красиво переводится с латинского как "сверхсуществующее". Справедливости ради, стоит отметить, что есть еще один способ записи трансцендентных чисел, называется бесконечный ряд, например, число π можно расписать в следующий ряд π = 4×(1/1-1/3+1/5-1/7+1/9-...). Подобный бесконечный ряд можно придумать для любого трансцендентного числа, но вот записать его в виде конечной формулы, получится далеко не для всякого. Число π же в свою очередь можно записать конечной формулой, открытой немецким математиком Лейбницом: 4×Σ(-1)ⁿ/(2n-1), на основе которой строится тот самый бесконечный ряд^[120].

Конечно число π особенное и играет важную роль в математике, но не все трансцендентные числа такие примечательные, количество трансцендентных чисел так велико, что заурядных среди них очень много, и практически все из них не выразишь никакой конечной формулой. Представим себе любой отрезок и на этом отрезке может существовать такая точка, которую нельзя описать никакой конечной дробью и никаким алгебраическим числом и вообще никакой конечной формулой. Более того отрезок содержит несчетное количество таких точек, каждая из которых является трансцендентным числом. Давайте проверим, так ли это. Разобьем наш отрезок на десять равных частей. Выделим какую-нибудь случайную часть, запишем ее номер (допустим 6) и снова разобьем ее на десять частей, снова запишем номер случайной части (допустим 7) и снова повторим эту операцию. Так мы можем делать бесконечно. В итоге мы получим бесконечную случайную последовательность чисел. Что-то вроде 6708112345... Иными словами мы получили бесконечную десятичную дробь 0,6708112345..., которая не является рациональным числом, и с большой долей вероятности не является алгебраическим числом, и скорее всего невыражаема никакой конечной формулой. Получается, что если случайно ткнуть в числовую прямую, то вы почти со стопроцентной вероятностью попадете в трансцендентное число.

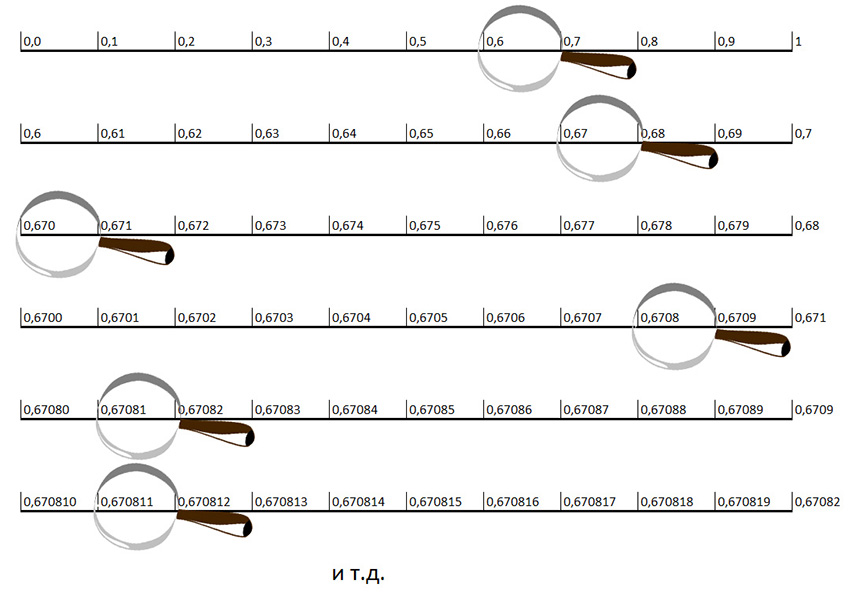
Понятно, что такие операции мы можем проделывать бесконечно, получая разные бесконечные последовательности чисел, то есть разные бесконечные десятичные дроби. Среди этих бесконечных десятичных дробей будут и трансцендентные числа (вроде π/4 ≈ 0,785398163397...), их будет большинство, и алгебраические числа (вроде √1/2 ≈ 0,707106781186...) и рациональные числа (вроде 1/7 ≈ 0,142857142857... или 67/100 = 0,6700000000...). Эти всевозможные бесконечные десятичные дроби и есть всевозможные точки, из которых состоит наш отрезок, всю эту совокупность называют действительными числами (иногда еще вещественными или реальными). Теперь давайте проверим, сможем ли мы сопоставить всю эту бесконечность действительных чисел с обычной бесконечностью натуральных чисел, типа {1,2,3,4,...}. Для этого нам снова понадобится наш бесконечный отель.

Пусть в него пытаются заселиться множество постояльцев, у каждого из которых есть бронь, обозначенная какой-нибудь бесконечной дробью, вроде той, которую мы получали выше (0,6708112345...), да так что среди этих людей встречаются всевозможные виды бесконечных дробей в их брони. Начнем с предположения, что наш отель способен заселить всех этих людей. Тогда у менеджера отеля должен быть список, где учтена каждая бронь, причем список этот должен быть полный и содержать любой возможный номер брони. То есть каждая бесконечная дробь между 0 и 1 должна появиться в каком-то конечном месте этого списка под каким-то номером. Допустим, выглядеть он будет примерно так:

Итак постояльцы с всевозможными бесконечными номерами брони символизируют все действительные числа от 0 до 1, а номера их брони в списке символизируют натуральные числа. Кантор понял, что эти множества не сопоставимы, то есть список не может быть полным и содержать всевозможные бесконечные дроби. Как бы мы его не составляли в нем всегда какие-то будут отсутствовать. Это легко показать, мы можем создать бесконечную дробь, которой точно нет в списке. Для этого сперва спустимся по диагонали и составим новое число из подчеркнутых цифр:

Получилась десятичная дробь 0,6975... Теперь возьмем эту дробь и изменим все ее цифры, заменяя каждую любой другой (заранее оговорив принципы замены). Например, мы могли бы изменить 6 на 3, 9 на 2, 7 на 5, а 5 на 1 и т.д. Соответственно, мы получим новую десятичную дробь 0,3251... По идее она должна соответствовать чей-то брони из наших жильцов. Но этой брони нет, и не может быть в нашем списке. Почему спросите вы?

Ну это легко показать: Бронь не является бронью первого номера, так как она имеет другую первую цифру, чем число, находящееся в этом номере. И бронь не является бронью второго номера, поскольку у него другая вторая цифра. Третьим номером это число тоже быть не может, ведь у него так же другая третья цифра. В общем, она отличается от n-ого числа с n-ным десятичным разрядом. Поэтому нигде не фигурирует в списке! Вывод таков: отель Гильберта не может разместить всех таких постояльцев. Более того число этих постояльцев так велико, что мы даже не можем составить список, чтобы всех их туда включить. Если вы правильно поняли аналогию, то мы пытались представить всевозможные точки на линии в качестве постояльцев. То есть у нас существует две разные количественные бесконечности, одна больше другой. Спрашивать во сколько раз или на сколько раз бессмысленно. Больше и все тут. Бесконечность точек на линии называется континуумом, она столь велика, что мы не можем ее сопоставить с обычной бесконечностью, какой бы участок линии мы не выбрали, точек внутри него всегда будет больше. Тоже касается точек на плоскости или точек в пространстве. Если мы возьмем самый крошечный участок пространства, который вы можете представить, точек в нем будет больше, чем бесконечность подобных участков в бесконечном пространстве. Бесконечное множество, которое нельзя сопоставить с бесконечностью натуральных чисел один к одному называется несчетным, и основной вывод к которому мы пришли: счетная бесконечность < несчетная бесконечность. Как я и говорил первым к такому выводу пришел Кантор^[121], именно за это многие математики того времени невзлюбили его, так же как и его теорию множеств, потому что это открытие было таким же переворотом в математическом мире, сродни тому как во времена Древней Греции Гиппас открыл неизвлекаемость некоторых квадратных корней.

Хорошо, но как со всем этим связано возведение в бесконечную степень, закономерно спросите вы, и как эта ситуация с бесконечными номерами брони связана с ситуацией когда мы пытались расселить бесконечное количество постояльцев, сгруппированных в бесконечной иерархии. Опять же так сразу понять не получится. Сперва, нам нужно узнать, как хранятся иррациональные числа в компьютере. Понятно, что иррациональное число это такое число, у которого бесконечная последовательность чисел, после запятой. А компьютер не может хранить бесконечную последовательность. Обычно хранится где-то 15 или 16 знаков после запятой, остальные округляются. То есть самое точное значение √2, которое можно использовать в обычной компьютерной программе это 1,414213562373109.

А можно ли повысить точность? В принципе можно, но чтобы понять, как, нужно разобрать как компьютер вообще хранит числа. Ну, это просто, совершим небольшой экскурс в информатику. Итак, сколько видов информации может хранить одна лампочка? Ответ очевиден: 2 – вкл и выкл. А две лампочки? Ответ: 4 – выкл+выкл, вкл+вкл, выкл+вкл, вкл+выкл. А если у нас n лампочек? Ответ: 2ⁿ - информации. Лампочки или любые другие единичные носители информации, которые могут иметь два состояние (вкл. и выкл.) в информатике условно называют битами. Выражение 2ⁿ - основа информатики, оно называется Булеан - количество видов информации, которое может закодировать компьютер имея в своем распоряжении память n-бит. То есть, имея 1 бит, мы можем закодировать числа от 0 до 1, имея 2 бита от 0 до 3, имея 8 бит от 0 до 255, имея 16 бит от 0 до 65535. Самые внимательные вспомнят, как я уже приводил в первой части в Таблице №5 максимальные числа, которые можно закодировать имея тот или иной объем памяти.

Однако обычно для хранения целых чисел отводится не более 32 бит, и этого считается достаточно для большинства расчетов, потому что 2³² = 4294967296. Хотя, если быть совсем точным, то 2³¹ = 2147483648, и куда же подевался еще один бит спросите вы, почему одна лампочка не участвует в кодировании числа. На самом деле этот последний бит кодирует знак минус, то есть, если эта лампочка горит, значит число отрицательное. Для хранения же дробных чисел используется 52 бита, что дает возможность записать любое дробное число в диапазоне от 0 до 1 с точностью 1/4503599627370496^[122]. Соответственно, чем больше мы определим бит для записи дробного числа, тем точнее оно может быть, ну или что тоже самое, тем бо́льшим мы сможем сделать его числитель или знаменатель. Раз мы выяснили, что у иррационального числа должен быть бесконечный числитель и знаменатель, ну либо оно имеет бесконечное количество цифр после запятой в десятичной записи, значит для точной записи такого числа необходимо бесконечное число бит. То есть бесконечное число бит позволит нам записать иррациональное число со всей его бесконечной точностью. А на самом деле, имея бесконечное число бит, мы сможем закодировать даже не одно иррациональное число, а всевозможные иррациональные числа. Получается бесконечность иррациональных чисел и бесконечность целых чисел должны соотноситься как 2ⁿ. Формула, которую вывел Кантор, гласит: 2^ℵ = континуум, ℵ < 2^ℵ.

В теории множеств булеан (2ⁿ) так же выполняет роль множества всех подмножеств. Вспомним девятую аксиому теории множеств, которая говорит о том, что для любого множества существует другое множество, такое что содержит все подмножества первого как элементы. Пустое множество ø = {} содержит ноль элементов и является само себе подмножеством (2⁰ = 1; булеан = {ø}). Множество с одним элементом {a} содержит в себе два подмножества собственно пустое и само себя (2¹ = 2; булеан = {ø,{a}}). Множество с двумя элементами {a,b} содержит в себе уже четыре подмножества (2² = 4; булеан = {ø,{a},{b},{a,b}}). Множество с тремя элементами {a,b,c} - восемь подмножеств (2³ = 8; булеан = {ø,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}), и так далее. Для тех кто силен в комбинаторике не вызовет сложности понимание того, почему множество всех подмножеств находится по формуле 2ⁿ, это всего лишь число размещений с повторениями для двух ситуаций (включать в подмножество "#1", или не включать в подмножество "#0") на элементы множества. Например: 2^{a} = {{a#0},{a#1}}, или 2^{a,b} = {{a#0,b#0},{a#0,b#1},{a#1,b#0},{a#1,b#1}}. Получается, что континуум является множеством всех подмножеств (булеаном) для бесконечного множества натуральных чисел (и как следствие для любого счетного бесконечного множества, потому что любое счетное бесконечное множество сопоставимо с множеством натуральных чисел). Существование континуума гарантирует Аксиома множества всех подмножеств, но она ничего не говорит о том какие элементы он должен содержать. Откуда мы вообще знаем, что возможны любые кобминации бесконечных последовательностей натуральных чисел. А это нам гарантирует Аксиома выбора, которая утверждает, что мы всегда можем составить произвольное подмножество из элементов множества, значит и для бесконечных множеств должно существовать множество всех возможных подмножеств.

Показать, что 2^ℵ = n^ℵ = ℵ^ℵ тоже несложно (не путайте с ординальным возведением в степень, в котором, напомню: 2^ω = n^ω = ω, где n < ω). Все современные компьютеры используют двоичный код, то есть единичный носитель информации - бит может быть в состоянии либо 0 (выкл), либо 1 (вкл). Но можно представить иные системы хранения информации, например троичную, где единичный носитель информации может принимать три состояния, или четверичную - где может принимать четыре состояния и т.д. Например, наша ДНК является четверичной системой кодирования информации. Перемычки в спирали ДНК, называемые нуклеотидами, которые и являются ее битами, могут состоять из четырех веществ: тимин (0), гуанин (1), аденин (2), цитозин (3). В такой системе кодирования можно хранить 4ⁿ видов информации, где n - число нуклеотидов. Как известно код ДНК уже повсеместно изучают при помощи компьютеров, а значит его смогли перевести в обычный двоичный код. Как это сделать сможет объяснить даже ученик 9 класса, если он на уроках информатики хорошо усвоил тему "перевод систем счисления". Понятно, что чем больше "...ичность" системы счисления, тем бо́льшее число я могу закодировать меньшим числом бит, но когда речь идет о бесконечности, это уже не имеет значения и поэтому 2^ℵ = n^ℵ. Кроме того, когда я говорю, что иррациональное число можно представить в виде бесконечной десятичной дроби, я на самом деле имею в виду кодирование 10^ℵ. Вот и получается, что не имеет значения по сколько будут сгруппированы уровни иерархии потенциальных инопланетных гостей нашего отеля, по 2 пассажира на корбаль, 2 корбаля на звено, и т.д., или по 3 пассажира на корабль, 3 корабля на звено, и т.д., все равно, если иерархия этих вложений бесконечная, мы не сможем заселить таких постояльцев в отель.

ℵ^ℵ - рассмотрим отдельно, это равносильно тому, что на каждом уровне бесконечной иерархии будет бесконечное количество представителей (бесконечное количество пассажиров на корабаль, бесконечное количество корбалей на звено, и т.д.). Докажем, что n^ℵ = ℵ^ℵ. Вообще применимо к информатике, ℵ^ℵ - значит, что у нас есть ℵ количество бит, каждый из которых может принимать ℵ количество состояний, то есть уже один бит способен закодировать любое натуральное число, потому что у него есть некое состояние для каждого числа, однако этого явно будет недостаточно для кодирования всей возможной счетной информации, два таких бита тоже не справятся, ведь ℵ×ℵ = ℵ² = ℵ, они смогут закодировать только два любых натуральных числа (с их помощью, например, можно будет выразить все множество дробей), три тоже не справятся ℵ×ℵ×ℵ = ℵ³ = ℵ, значит нам по-прежнему необходимо ℵ количество бит, и следовательно ℵ^ℵ = континуум.

Есть еще одна интересная особенность ℵ^ℵ, о которой следует поговорить. Давайте вспомним как нашему менеджеру было необходимо не только расселять пассажиров, но и пересчитывать их, для этого он использовал трансфинитные ординалы. Бесконечные пассажиры бесконечных автобусов упорядочивались ω², но их количество было равно |ω²| = ℵ² = ℵ, бесконечные пассажиры бесконечных вагонов бесконечных поездов упорядочивались ω³, но их количество было равно |ω³| = ℵ³ = ℵ, бесконечные пассажиры бесконечных вагонов бесконечных поездов бесконечных паромов упорядочивались ω⁴, но их количество тоже было равно |ω⁴| = ℵ⁴ = ℵ, и так далее. Но как представить неоднородность бесконечности, которая упорядочивается ординалом ω^ω или даже еще бо́льшим счетным ординалом. Ведь как мы помним |ω^ω| = ℵ ≠ ℵ^ℵ, а в случае с бесконечной вложенностью число пассажиров становится ℵ^ℵ - несчетным.

Тут есть одна хитрость, которая позволит бесконечную вложенность сделать счетной, она основана на одном из свойств счетных множеств, согласно которому множество всех конечных подмножеств любого счётного множества всегда счётно^[111]. Иными словами нужно создать такую бесконечную вложенность, которую мы могли бы разбить на конечные подмножества, то есть нужно сделать так чтобы каждый кто заселяется в наш отель имел бы конкретный счетный ординальный номер. Ведь счетность подразумевает наличие счета, так чтобы один элемент можно было бы отличить от другого. Если взять пример с бесконечным числом точек в отрезке, и поставить в нем точку посередине отрезка, так чтобы ей можно было бы присвоить десятичную дробь 0,5 то совершенно непонятно какая точка будет следующей 0,51 или 0,501 или 0,5001 или... В то время как счетное множество всегда позволяет отличить два соседних элемента при помощи упорядочивания счетными ординалами. Так например, между ординалами ω³+ω²×2 и ω³+ω²×2+1 нет никаких промежуточных ординалов, значит второй ординал точно следует за первым ординалом. Получается, что счетным является то множество, которое можно упорядочить счетными ординалами. В случае с бесконечно вложенным флотом, такое сделать не получится, нельзя сказать на каком конкретном корабле летит некий пассажир, в какое конкретное звено входит этот корабль, в какую конкретную эскадру входит звено, в какую конкретную флотилию входит эскадра, в какую конкретную армаду входит флотилия и так далее. Даже если бы мы сделали так чтобы на каждом уровне было бы не более десяти вариантов, и мы бы записывали номер пассажира, корабля, звена, эскадры, флотилии, армады, и т.д., то учитывая бесконечную вложенность этой иерархии мы получили бы бесконечное десятичное число, которое естественно не является конечным подмножеством. Это почти как в примере со всевозможными номерами бесконечной брони у заселяющихся, только теперь мы имеем пассажиров со всевозможными номерами бесконечного адреса их положения во флоте. Ну и как мы уже знаем, вся эта совокупность пассажиров будет континуумом, который несчетен и не может быть заселен в отель. Все потому что идентификация заселяющихся в обоих примерах не может быть записана конечным способом, или говоря на языке теории множеств, нет возможности разбить множество на конечные подмножества, так чтобы их совокупность была счетной.

Но вот вам пример бесконечной вложенности, которую можно разбить на счетное множество конечных подмножеств, так чтобы каждый элемент можно было бы пронумеровать неким счетным ординалом. Пусть все инопланетные гости прилетят к нам на одном большом корабле-носителе, и пусть он содержит в себе бесконечное количество пассажиров и бесконечное количество других космических кораблей. Каждый из космических кораблей, которые он содержит, так же включает в себя бесконечное количество пассажиров и бесконечное количество кораблей, и так далее... Получаем бесконечную вложенность, но очевидно она отличается от той бесконечной вложенности что была ранее, и главное отличие в том, что каждый пассажир теперь может получить идентификатор, который можно записать конечным способом. Для того чтобы всех индентифицировать так же воспользуемся трансфинитными ординалами. На первом уровне у нас один космический корабль. Всех пассажиров, которые на нем находятся, пронумеруем обычными натуральными числами - n. Так же этот корабль содержит бесконечное количество других кораблей, на которых пассажиры получат идентификационный номер: ω×k+n, где n - номер пассажира, а k - номер корабля. Это был второй уровень вложенности. На третьем уровне вложенности идентификационный номер определяется по принципу: ω²×l+ω×k+n, где n - номер пассажира, k - номер корабля, l - номер корабля на котором находится этот корабль. Для четвертого уровня вложенности так же получаем формулу идентификации пассажиров: ω³×m+ω²×l+ω×k+n, где n - номер пассажира, k - номер корабля второго уровня, l - номер корабля третьего уровня, m - номер корабля четвертого уровня. И так далее по всей бесконечной вложености, каждый корабль в этой иерархической вложенности получает номер кратный ωⁿ, где n - уровень вложенности. Получается, что на каком бы уровне вложенности не находился пассажир, он все равно получит свой номер, который теоретически можно записать конечным способом, а значит менеджер отеля может составить рекурсивную формулу, которая распределит их по номерам. Как вы должны помнить для упорядочивания всей этой неоднородной бесконечности нам нужен еще один номер, пусть помимо всей этой процессии инопланетян в наш отель заселяется еще один постоялец, тогда он получит номер ω^ω, то есть возможность разбиения бесконечной вложенности на конечные подмножества позволяет присвоить ей счетный упорядочивающий ординал и сопоставить с бесконечностью натуральных чисел. Вам может показаться все это каким-то не интуитивным, почему от способа организации бесконечной вложенности бесконечностей зависит является ли она счетной или нет, но так уж устроена теория множеств.

Что касается формулы заселения всех этих пассажиров а наш отель, то для нее подойдет метод факторизации простых чисел, но метод сиплексного распределения уже не годится. Дело в том, что, как мы выяснили, симплексное распределение это не расширяемый метод, который может работать только с конкретным конечным уровнем вложения бесконечностей. Факторизация простых чисел же позволяет одновременно заселять пассажиров сгруппированных в разные уровни вложенности. В основе этого метода лежит основная теорема арифметики, которая гласит: любое число не явлющиеся простым можно представить в виде уникального произведения простых множителей. Ключевое слово здесь уникальное произведение, и действительно, если мы попробуем разложить любое непростое число на множители, то получим уникальное сочетание простых чисел: 4 = 2×2 = 2²; 6 = 2×3 = 2¹×3¹; 8 = 2×2×2 = 2³; 10 = 2×5 = 2¹×5¹; 12 = 2×2×3 = 2²×3¹; и т.д. Эта теорема лежит в основе большинства криптографических систем, что защищают наши счета в банках, потому что процедура разложения больших чисел на простые множители невероятно сложна даже для компьютеров. А еще эта теорема гарантирует, что при использовании метода факторизации простых чисел, каждый пассажир из описанного выше корабля-носителя с бесконечной вложенностью получит место в отеле. Поскольку каждый пассажир имеет конечный адрес в этой вложенности, то он просто должен взять столько простых чисел, сколько соответствует его уровню вложенности, каждое простое число возвести в степень равную номеру его корабля на каждом уровне вложенности и все перемножить (основание двойки при этом следует оставить для получения собственного номера в составе корабля, в котором пассажир непосредственно находится). Более формально формула будет выглядеть так: N = 2^k₁×3^k₂×5^k₃×7^k₄×...×p_n^k_n, где k₁ - номер пассажира в корабле, в котором он непосредственно находится, k₂ - номер корабля, в следующем уровне вложенности, k_n - номер корабля, в n-ному уровне вложенности, относительно данного пассажира. Так как все пассажиры имеют конечный адрес, значит у каждого конкретно взятого пассажира будет конечный уровень вложенности. Следовательно все пассажиры из нашего корабля-носителя расселятся по номерам отеля. Причем, если считать все номера не с нуля как мы договороились, а с единицы, то тогда займут они только номера соответствующие непростым числам, и у нас еще по-прежнему останется бесконечность номеров соответствующих простым числам.

Распределение пассажиров в таком космическом корабле-носителе с бесконечной вложенностью эквивалентено множеству всех алгебраических чисел, которое так же упорядочивается ординалом ω^ω. Но ничто не мешает нам продолжать создавать дальнейшие рекурсии, при условии сохранения разбиения на конечные подмножества. Пусть теперь инопланетяне будут иметь два вида космических кораблей: космические крейсеры и космические фрегаты. Но чтобы не возник континуум, они должны так же прибыть к нам в одном бесконечном корабле-носителе, пусть он будет из класса крейсеров. Итак теперь условия вложенности такие: в каждом крейсере содержится бесконечное количество других крейсеров, а так же содержится бесконечное количество фрегатов, и бесконечное количество пассажиров. В каждом фрегате при этом содержится бесконечное количество других фрегатов и бесконечное количество пассажиров. Так же расмотрим уровни вложенности по возрастающей. На первом уровне у нас крейсер-носитель. Все фрегаты, входящие в начальный крейсер-носитель, имеют бесконечный уровень вложенности и каждый из входящих в них фрегат будет иметь номер кратный ωⁿ, где n - уровень вложенности, так что все пассажиры будут на них учтены тем же методом, что мы использовали выше. Тогда пассажиры летящие на первом крейсере, что входит в начальный крейсер-носитель, получат номера ω^ω+n, а все фрегаты что на нем находятся получат номера ω^ω+ωⁿ, и всех пассажиров на них можно учесть похожим образом. Все что входит во второй крейсер, входящий в начальный крейсер-носитель, получит номера "ω^ω×2+...", и так далее, все что входит в n-ный крейсер, входящий в начальный крейсер-носитель, получит номера "ω^ω×n+...". Это мы только разобрались со вторым уровнем вложенности. Тогда на третьем уровне вложенности все крейсеры будут нумероваться ω^ω+1×n, на четвертом уровне получат номера ω^ω+2×n, и так далее, ну а все фрегаты на них будут иметь подномера "...+ωⁿ", в зависимости от их собственного уровня вложенности, и для нумерации пассажира находящегося на каждом из корбалей необходимо будет добавить только "...+n", в зависимости от его собственного порядкового номера. И получается все будут учтены так, что получат конечный идентификатор, а значит мы сможем заселить их в наш отель. Упорядочиваться такая иерархия будет ординалом ω^ω×2. Если мы все усложним так, что в нашей бесконечной вложенности будет участвовать три вида кораблей, то получим неоднородную бесконечность уровня ω^ω×3, ну и соответственно если возьмем n видов кораблей, то упорядоченность будет ω^ω×n. С бесконечным количеством видов кораблей, к сожалению, счетного множества не выйдет, мы снова получим континуум, потому что тут опять исчезнет возможность дать каждому пассажиру конечный идентификатор. Однако можно привести другой способ организовать бесконечную вложенность, так чтобы она была еще более рекурсивной, и при этом так же разбивалась на конечные подмножества, просто дальше придумывать примеры мне уже не позволяет фантазия.

Расселять такие множества можно тоже с применением метода факторизации простых чисел, только его необходимо немного модифицировать. Так например, если бесконечная вложенность сгруппирована с использованием двух видов кораблей, то необходимо так же особым способом группировать простые числа в основании. Показатель двойки так же оставим для обозначения места в корабле, в котором непосредственно находится пассажир, но у каждых следующих двух простых чисел показатели будут соответствовать разным вложенностям, у первого из этих чисел показатель будет обозначать уровень вложенности крейсера, а у второго из этих чисел уровень вложенности фрегата. Так как каждая из этих вложенностей для конкретно взятого пассажира конечна, то и общее число используемых простых чисел тоже будет конечно. Формально формула будет выглядеть так: N = 2ⁿ×3^k₁×5^f₁×7^k₂×11^f₂×...×p_2n^k_n/2×p_2n+1^f_n/2+1. Если же какой-то из видов кораблей образует иерархию меньшей вложености чем другой, то мы просто не будем использовать соответствующие простые числа. Так разбив факторизацию на четные (n/2) и нечетные (n/2+1) элементы, каждой группе присвоив соотвествующий вид бесконечной вложенности, мы смогли заселить в отель неоднородность бесконечности с упорядоченостью ω^ω×2. Получается, что для заселения неоднородной бесконечности с упорядоченостью ω^ω×3 (например, когда в бесконечной вложенности используется три вида кораблей) достаточно так же разделить факторизацию на элементы кратные трем (n/3), элементы, которые дают 1 в остатке при делени на три (n/3+1), и элементы, которые дают 2 в остатке при делени на три (n/3+2), и  тогда все пассажиры так же благополучно заселяться в бесконечный отель. Используя этот принцип, можно расселять пассажиров сгруппированых с бесконечной вложенность любого вида кораблей (конечно при условии, что у нас есть начальный корабль-носитель).

Кроме примеров с бесконечными пассажирами, мы так же можем определить бо́льшие меры неупорядоченности на некоторых счетных подмножествах действительных чисел. Но для этого нам придется серьезно погрузиться в алгебру и математический анализ, однако для тех, кто сильно не любит эти разделы математики, следующие четыре абзаца могут показаться сложными и неинтерсными, и такие читатели могут смело пропустить их, не потеряв какой-то важной для нашей темы информации. Остальным же я предлагаю вспомнить что такое рациональные выражения. Это такие формулы, которые можно записать в виде дроби составленной из многочленов (axⁿ+bx^n-1+...)/(wxⁿ+vx^n-1+...), так же их можно переписать в виде многочлена, который может содержать отрицательные степени, например: ax²+bx¹+cx⁰+wx^-1+vx^-2; где во всех этих выражениях x - является свободной перменной. Еще в школе в восьмом класса учат, что все уравенения с рациональными выражениями можно привести к обычным степенным уравнениям axⁿ+bx^n-1+cx^n-2+... = 0, или, говоря математическим языком, к многочлену приравненному к нулю. Как мы с вами выяснили, всевозможные решения степенных уравенений составляют множество алгебраических чисел, которое имеет упорядоченность ω^ω. Это потому что всякий раз, увеличивая количество членов в многочлене, в соотвествии с правилами комбинаторики, мы создаем неоднородность в бесконечности количества решений: ω×ω×ω×...n-раз, а если мы говорим о всех возможных многочленах тогда неоднородность будет: ω×ω×ω×... ω-раз, что равно ω^ω_. Однако уже в девятом классе учителя математики объясняют, что рациональные неравенства в отличие от рациональных уравнений, нельзя так просто сводить к степенным неравенствам. А если кто вспомнит аналитическую геометрию из того же курса девятого класса, то он вероятно так же вспомнит, что при помощи систем неравенств можно рисовать фигуры. Так вот, нас интересуют числа, измеряющие площади этих фигур. В математике такие числа называют периодами, и они определяются как всевозможные интегралы рациональных функций, то есть всевозможные площади, которые создаются на графике степенными неравествами. И если мы будем говорить про интегралы, то вам придется вспомнить математический анализ уже из старших классов, но достаточно знания того что интеграл это как раз и есть площадь органиченная линией графика и определенная в некотором интервале этого графика. Периоды - это пока еще малоизученный класс чисел, но математики точно знают, что он образует счетное множество^[123]. Упорядоченность всех возможных периодов еще до конца не изучена, поэтому мы и не будем разбирать все возможные периоды, остановимся только на некоторых. Но сперва давайте поймем, что основной вклад в разнообразие интегралов вносит именно размер интегрируемого интервала, а не относительное значение его границ. Поскольку мы рассматриваем все возможные рациональные функции, то с учетом их возможных сдвигов, мы получим одинаковые числа при интегрировании, если будем двигать функцию вместе с интегрируемым интервалом. Например, площадь под графиком обычной параболы не изменится, если мы сдвинем параболу влево вместе с исследуемым интервалом. Поэтому у любого интеграла _β∫^α нас будет интересовать именно длина интервала, на котором он определен, |α-β|.

Для начала возьмем интегралы рациональных выражений определенные в целых интервалах (площади ограниченные графиком в интервале между целыми значениями). Попробуем упорядочить множество получившихся чисел. И прежде всего надо сказать, что несмотря на то, что рациональные выражения могут содержать многочлены с отрицательными степенями или, если записаны в виде дроби, то могут содержать два многочлена (в числителе и знаменателе), все равно общее количество членов всегда будет конечно, аналогично обычным степенным многочленам, и каждому такому выражению можно будет сопоставить некий ординал меньший чем ω^ω. Теперь внимание, чтобы так же присвоить некий ординал каждому интегралу от таких выражений с натуральным n-ным размером интегрируемого интервала, нужно просто добавить "ω^ω×n+..." к ординалу полученному при нумерации многочлена (где n - размер интервала), и все, мы сможем всех их индентифицировать. Тогда получается, что все интегралы рациональных выражений с натуральными интервалами будут упорядочены ординалом ω^ω×ω = ω^ω+1. Итак мы уже получили бесконечное счетное множество с бо́льшей неоднородностью, чем можно получить решением всех степенных уравнений. Все алгебраические числа входят в состав этого множества, но так же туда входят и некоторые трансцендентые числа (но не все), например число π, потому что число π = ₀∫¹4/(x²+1).

Теперь можем подступиться к интегралам рациональных выражений определенных в дробных интервалах (площади ограниченные графиком в интервале между дробными значениями). Поскольку все возможные длины интервалов будут неким дробным числом m/n, то в этом случае нумерация тоже будет простой, для того чтобы каждому интегралу дать уникальный номер, нужно к ординалу полученному при нумерации многочлена добавить "ω^ω+1×m+ω^ω×n+...". Общая же упорядоченность, как не трудно посчитать, будет равна ω^ω×ω×ω = ω^ω+2. Принцип подсчета прост: множество всех возможных многочленов, упорядочиваемых ω^ω, комбинируется с множеством возможных натуральных значений числителя m в длине интервала, упорядочиваемых ω, и множеством возможных натуральных значений знаменателя n в длине интервала, так же упорядочиваемых ω - и все это по правилам комбинаторики мы должны перемножить. Или можно было сразу ω^ω умножать на ω², ординал выражающий упорядоченность множества всех дробей, ω^ω×ω² = ω^ω+2. И если воспользоваться этим принципом, можно будет упорядочить множества интегралов определенных на более сложных интервалах. Так например, если длины интервалов будут всевозможными числами, которые можно получить при решении квадратных уравнений, то мера упорядоченности множества таких интегралов рациональных выражений будет равна ω^ω×ω³ = ω^ω+3, потому что множество решений квадратных уравнений упорядочивается ординалом ω³. И так далее, если мы будем увеличивать упорядоченность множеств чисел, которыми может быть ограничен интергируемый интервал, то мера упорядоченности множества всех таких интегралов тоже будет расти. И уже множество интегралов определенных на любых алгебраических интервалах (площади ограниченные графиком в интервале между любыми алгебраическими значениями), будет иметь упорядоченность ω^ω×ω^ω = ω^ω×2, все по тому же принципу, упорядоченность множества возможных интегрируемых многочленов перемножаем на упорядоченность множества решений степенных уравнений. Можем пойти еще дальше и определить множество интегралов определеных на интервалах, которые ограниченны всевозможными значениями интегралов с алгебраическими интервалами, тогда комбинаторика их упорядоченности даст нам ординал: ω^ω×ω^ω×ω^ω = ω^ω×3. Можно и дальше увеличивать вложенность интегралов, получая все бо́льшую неупорядоченность их множества, для идентификации каждого элемента которого понадобится все бо́льший ординал ω^ω×n. Тогда совокупность всех интегралов имеющих конечный уровень вложенности будет иметь упорядоченность равную ω^ω2 = ω^ω×ω. Однако нельзя допускать бесконечной вложенности интегралов, иначе мы так же получим континуум. Но есть и другие способы определить интегралы на рациональных выражениях, например с использованием бесконечных интервалов, или задействуя двойные интегралы, так что получится еще бо́льшая неупорядоченность^[124]. В целом, как я и говорил, изучение таких чисел, называемых периодами (что являются интергральными площадами), это сейчас актуальное направление в математике, и их общая упорядоченность еще не до конца изучена, но математики уверены что вся их совокупность это счетное множество. Мы же для рассмотрения бо́льших упорядоченностей перейдем к другим более простым примерам.

Алгебра не ограничивается только степеными уравнениями, и если мы возьмем на вооружение показательные уравнения, то мы сможем создать еще бо́льшую неоднородность в бесконечности, которую придется упорядочивать еще бо́льшим ординалом. Для начала установим тот факт, что решения показательных уравнений вида a^xn+b^x(n-1)+... = 0, так же будут иметь упорядоченность равную ω^ω, поскольку здесь применима та же логика как и со степенными уравнениями, их похожим образом можно составить из суммы приозвольного количества членов a_n^nx, где a_n - произвольное натуральное число. Решение таких уравнений сводится к методам подстановки и приведения к степенному уравнению с последующим логарифмированием результатов решения. Так например, уравнение 2^2x-8×2^x+15=0 будет так же иметь два решения (log₂3 и log₂5), как и уравнение x²-8x+15=0, которое тоже будет иметь два решения (3 и 5), подстановкой и логарифмированием которых, первое в итоге и решается. Конечно множество всех решений таких показательных уравнений не будет совпадать с множеством алгебраических чисел, это будут другие числа, большинство из которых будут трансцендентными (например, в составе множества этих чисел нам встретятся всевозможные логарифмы рациональных чисел), но их упорядоченность так же как и упорядоченность алгебраических чисел будет равна лишь ω^ω. Однако, если мы допустим что показательное уравнение будет составлено из суммы членов, в показателе которых находится многолен второй степени a^mx2+nx, то множество решений всех таких уравнений может быть упорядоченно уже только ординалом ω^ω2, поскольку комбинации всех возможных членов таких уравнений мы будем счиатать так: всевозможные a_n^nx (ω^ω) умножаем на всевозможные a_n^x2+nx (ω^ω) умножаем на всевозможные a_n^2x2+nx (ω^ω) ... и так далее... умножаем на всевозможные a_n^mx2+nx (ω^ω)... бесконечное количество раз, что и даст нам ординал ω^ω2 = ω^ω×ω^ω×ω^ω×... ω-раз. Тогда продолжим усложнять показательные уравнения, и пусть теперь в показателе суммирующихся членов будет возможен многочлен третьей степени: a^kx3+mx2+nx, не трудно догадаться, что в этом случае упорядочить все решения таких уравнений можно будет лишь ординалом ω^ω3. В общем случае же сделаем вывод, что множество решений всех показательных уравений составленных из суммы членов, в показателе которых может быть любой многочлен n-ной степени, будет упорядочиваться ординалом ω^ωω. Расселять все такие числа в отель (сопоставлять с натуральным рядом) будем с использованием формулы факторизации факторизации, это когда показатель степени простого числа сам по себе распределяется по методу факторизации простого числа.

Можно создавать и более сложные показательные уравения, тем самым, увеличивая неоднородность в множестве решений всех их возможных вариантов, так чтобы для их перечисления нам требовались еще бо́льшие ординалы, вплоть до ω^ωωω..., но имеет ли это смысл, ведь согласно Теореме Абеля мы не можем выразить привычным нам способом (как минимум с использованием корней) решения даже уравнений пятой степени, что упорядочиваются ординалом ω⁶. Тем не менее, это действенный способ расширения счетного множества алгебраических чисел, путем добавления в него счетных подмножеств трансцендентных чисел, которые потенциально могут буть решениями таких уравнений. При этом в бесконечности этих решений создается такая неоднородность, что для ее описания нам необходимо использовать все б́ольший уровень рекурсии для вложенности бесконечностей, измеряемый все бо́льшими счетными ординалами. Так например, поднимая наш x в уравнении на более высокие этажи степенной башни, мы получаем множество всех видов таких уравений и соответственно всех их решений, упорядочиваемое ординалом в виде степенной башни построенной из ω, той же высоты что и исходное уравнение^[113].  Но даже ординал ω^ωωω... не предел для такой рекурсивной вложенности, теория множеств позволяет создавать еще бо́льшие неоднородности в счетных множествах трансцендентных чисел. Получается что рекурсии на ординалах это не только способы для выделения все более разряженных подмножеств натуральных чисел (что необходимо нам в гугологии для создания больших чисел), а поскольку любое счетное множество можно сопоставить один к одному с натуральными числами, то рекурсии на ординалах это еще и способы выделения из континуума все более богатых счетных подмножеств трансцендентных чисел.

И пусть нам неизветны конечные способы записи большинства таких чисел, для любого числа из таких получившихся множеств, чисто теоретически, можно написать алгоритм его вычисления на компьютере. Все такие числа называются вычислимые (computable numbers) и это тоже счетное множество. Позже вы увидите, что даже множество чисел, которые невозможно вычислить на компьютере, но можно описать на языке какой-либо теории (definable numbers), тоже может быть счетным, при условии, что его можно разбить на непересекающиеся конечные подмножества. А раз любые счетные множества можно один к одному сопоставить с натуральными числами, то методы такого сопоставления дадут нам так же возможность сильно разрядить последовательность натуральных чисел при помощи быстрорастущих функций, чтобы создать очень большие числа. Тогда получается что можно создать большие натуральные числа, которые будут вычислимые в некой теории, и при этом будут записаны разумно конечной формулой, а можно создать еще бо́льшие натуральные числа, которые будут невычислимые в данной теории, но эта теория все еще будет способна определить их с помощью сверхрекурсивной конечной формулы. Но это я пока сильно забегаю вперед. Однако основную идею вы должны уловить, счетный ординал, который будет упорядочивать все получившиеся таким образом счетные множества, так же, по сути, определяет размеры натуральных чисел потенциально создаваемые с помощью формул "расселения" этих множеств по натуральному ряду. По сути всю оставшуюся часть книги мы и будем изучать данные ординалы.

Континуум же в свою очередь нельзя разбить на непересекающиеся подмножества, так чтобы они были конечными. Как бы мы не пытались выделить из него счетное множество чисел, всегда останутся трансцендентные числа не входящие в него и их множество будет несчетным. Поэтому континуум создается, только если мы никак не идентифицируем вложенность бесконечностей (то есть не оставляем никакой возможности для разбиения на конечные подмножества), тогда все что мы можем сказать о порядке этого множества можно выразить лишь так |ω^ℵ| = ℵ^ℵ , и мы не можем определить о каком именно счетном ординале в показателе степени идет речь.

Ну и вы должны понимать, что по величине континуум будет больше любого счетного ординала, потому что нет возможности сопоставить каждому трансцендентному числу, некую конечную формулу, которая бы его определяла (нельзя записать каждое трансцендентное число конечным способом). Давайте на некоторых примерах и аналогиях еще раз проследим это и прочувствуем, почему континуум всегда больше любого счетного множества.

В рассказе Хорхе Борхеса Вавилонская библиотека^[125], упоминалась библиотека, которая содержала книги, и каждая была примерно по четыреста страниц, по сорок строк на страницу, и по восемдесят символов на строку, и символы были написанны либо латинским алфавитом, либо пунктуационными знаками, так что в каждой книге все символы были уникальным образом скомбинированы, и всего этих книг было столько, что среди них можно было найти любую комбинацию символов, но при этом ни одна книга не повторялась. Как отмечал сам писатель, большинство книг содержало просто сумбурный набор символов, но так же среди них можно было бы найти трактаты о всех событиях, которые уже случились, и всех которые еще только случатся, а так же многотомный каталог самой библиотеки, и множество многотомных фальшивых каталогов этой библиотеки, и даже многотомные трактаты доказывающие фальшивость этих каталогов. Все же число книг в такой библиотеке было конечным, и мы даже можем посчитать сколько их было, и приблизительно получим число 10^2000000 (число с двумя миллионами нулей после единицы). Естественно такая библиотека не поместилась бы внутри наблюдаемой вселенной, но вот в мастшабах всей вселенной, которые предсказывает инфляционная космология, ее вполне можно было бы уместить.

Нас же интересует несколько иная версия Вавилонской библиотеки, в которой содержатся книги любого размера (то есть содержащие любое конечное количество символов). Такая библиотека будет бесконечной, и что самое интересное, количество книг в ней будет счетно. В качестве доказательства так же используем какой-нибудь метод сопоставления с натуральными числами, допустим мы хотим раздать эти книги постояльцам нашего бесконечного отеля, если получится это сделать, значит бесконечность книг счетная. Давайте пронумеруем все символы двухзначными числами с сохранением незначащих нулей, например: 01 - A, 02 - B, 03 - С, 04 - D, и т.д., даже с учетом пунктуации наберется не более 40 чисел. Тогда, получается, каждой книге присвоено какое-то натуральное число, которое можно получить просто записав подряд все коды символов, что есть в этой книге. Теперь остается раздать их постояльцем отеля в соответствии с номерами их комнат. Да, такой метод распределения самый простой, но далеко не идельный, некоторые постояльцы, например, из комнат 556, 8092 и т.п., останутся без книг, но тем не менее это доказывает счетность множества книг. Даже если книги будут написаны с использованием вообще любых символов, множество книг все равно будет счетное, потому что мы по-прежнему, используя счетные ординалы, сможем конечным способом идентифицировать каждую книгу. И нечто похожее мы уже делали. Так книги с одним символом получат номер n₁, книги с двумя символами получат номера ω×n₂+n₁, книги с тремя символами получат номера ω²×n₃+ω×n₂+n₁, с четырьма символами ω³×n₄+ω²×n₃+ω×n₂+n₁, и так далее, как вы догадались, множество всех таких книг будет упорядочиваться ординалом ω^ω. Чтобы раздать все такие книги постояльцам бесконечного отеля можно так же воспользоваться методом факторизации простых чисел. Книги с одним символом достанутся комнатам 2^n₁, где n₁ - порядковый алфавитный номер этого символа. Книги с двумя символами достанутся комнатам 2^n₁×3^n₂, где так же n₁ - порядковый алфавитный номер первого символа, а n₂ - порядковый алфавитный номер второго символа. Книги с тремя символами получат комнаты 2^n₁×3^n₂×5^n₃, с четырьмя символами - комнаты 2^n₁×3^n₂×5^n₃×7^n₄, и так далее. Если же символы нумеровать не с нуля, а с единицы, то постояльцам комнат с простыми номерами книг и вовсе не достанется. И мы доказали, что даже библиотека с книгами, в которых найдется любой текст конечной длины с бесконечным количеством видов символом, остается счетной. Хочу так же обратить ваше внимание, что такой способ упорядочивания и раздачи книг постояльцам (ω^ω) будет работать только если книги в библиотеке расставлены в порядке возрастания размера содержимого. Если порядок расстановки книг будет другой, то упорядочиваться книги будут уже другим ординалом, и с тем насколько велики могут быть ординалы таких упорядочиваний мы еще познакомимся в дальнейшем, однако все равно все они будут счетными.

Это нас подводит к доказательству того, почему нельзя все трансцедентные числа описать конечным способом. Ведь по сути наша бесконечная библиотека содержала вообще все возможные книги, но при этом, оставалась счетно-бесконечной. А как мы знаем, множество всех трансцендентных чисел несчетно и составляет континуум, который больше любого счетного множества, значит есть такие трансцендентные числа, которые не могут быть описаны в этой библиотеке. Есть и более наглядное доказательство, похожее на диагональный аргумент Кантора (который в нашем примере со всевозожными бронями постояльцев доказывал несчетность континуума), и называется оно Парадокс Ришара, в честь французкого математика впервые его описавшего^[126]. Допустим в нашей библиотеке остались только книги, которые как-то конечным способом характеризуют какие-то трансцендентные числа, как например, число пи - отношение окружности к диаметру или π = ₀∫¹4/(x²+1), даже более того, пусть будет по одной книге характеризующей какое-то конкретное трансцендентное число (неважно каким способом, но главное - конечным). Как-то пронумеруем эти книги, назовем это нумерацией Ришара, а номер книги n-ным числом Ришара. И рассмотрим книгу в которой написано такое определение: "трансцендентное число, у которого в записи в виде бесконечной десятичной дроби: n-ная цифра равна 1, если у n-ного числа Ришара n-ная цифра не равна 1; и n-ная цифра равна 2, если у n-ного числа Ришара n-ная цифра равна 1". Получается противоречие, поскольку если это число является n-ным числом Ришара, то оно должно отличаться в n-ной цифре от n-ного числа Ришара. Этот парадокс еще раз доказывает, что трансцендентных чисел так много, что как бы мы не пытались, мы не сможем дать им всем конечные имена.

Ну и конечно же, если Вавилонская библиотека будет содержать бесконечное количество книг, где в каждой будет бесконечное количество символов, тогда общее количество таких книг будет несчетно и является континуумом. Тогда в такой библиотеке вам встретятся всевозможные трансцендентные числа. Причем, вы уже понимаете, что неважно сколько видов символов мы при этом будем использовать в книгах, главное чтобы не меньше двух (пусть даже бесконечное количество видов), потому что еще в примерах с кодированием бесконечной информации мы выяснили, что 2^ℵ = n^ℵ = ℵ^ℵ = континуум. Однако все эти бесконечные библиотеки с бесконечными книгами, бесконечный флот с бесконечной иерархией вложенности, и даже бесконечные постояльцы с бесконечно возможными номерами брони - все это слишком абстарктные примеры континуума, которые сложно наглядно визуализировать. Самым наглядным примером остается непрерывная последовательность точек на линии, и совсем неважно какого эта линия размера. Но нам сложно думать о точках как об отдельных элементах, поскольку мы видим только непрерывную линию. Есть и другие более наглядные способы визуализации континуума, которые позволяют думать о нем как о множестве отдельных элементов.

Один из наглядных способов называется бесконечным двоичным древом. Визуализируетя очень просто, представьте что из некого корня растет дерево, так что сразу разделяется на два ствола, после чего эти два ствола разделяются еще на два, а те, в свою очередь, еще на два ствола и так далее до бесконечности. На Рисунке №48.1 мы изобразим такое древо растущее вниз, вашему воображению остается только сделать его бесконечным. Наше дерево растет вниз, потому что так принято изображать его в теории графов, в которой правильным названием дерева будет связанный ациклический граф. И раз уж мы взялись за терминологию, то все промежуточные стволы этого дерева принято называть ребрами графа, а узлы из которых они растут - вершинами графа. Так корень тоже является вершиной, и если бы дерево было конечным то его окончания, тоже бы назывались вершинами. У бесконечного дерева окончаний быть не может, но корень и все узлы, мы отныне будем называть вершинами, как и принято в теории графов. Так вот, количество вершин в этом древе будет счетно-бесконечным, потому что каждую конкретную вершину легко пронумеровать, для этого нам нужны всего два натуральных числа: уровень вершины (m) и ее порядковый номер (n) на этом уровне. Сопоставление с натуральными числами можно будет выполнить по очень простой формуле N = 2^m-n. По сути, мы получили, неоднородность уровня ω², что количественно: ℵ² = ℵ. Та же самая логика подходит и для учета всех ребер графа, их количество так же будет счетно-бесконечным, трансфинитная нумерация будет точно такая же, а формула сопоставления с натуральными числами станет немного другой N = 2^m+1-n-1.

Где же в этом дереве спрятался континуум спросите вы, если число всех элементов его составляющих счетно. Несчетным в этом дереве будет являться количество всех возможных путей по нему, начиная от корня. Один из таких возможных путей отмечен красным на Рисунке №48.2. Доказать что число таких путей соответствует континууму достаточно просто. Давайте каждое ребро, ведущее влево отметим нулем, а каждое ребро, ведущее вправо отметим единицей. Если вы еще раз внимательно посмотрите на рисунок, вообразив так же, что дерево бесконечное, то вы поймете, что количество всех возможных путей будет соответствовать всем возможным кобинациям бесконечным последовательностей нулей и единиц. А это тоже самое что сказать, что у нас бесконечное количество бит, кодирует нулями и единицами всю возможную информацию, то есть 2^ℵ = континуум. Получается, что количественно число вершин и ребер бесконечного двоичного дерева меньше чем количество всех возможных путей по нему. Интересно, что для конечного дерева ситуация будет совсем иной. У конечного дерева вершин наберется 2ⁿ-1, ребер при этом всегда будет на одно меньше 2ⁿ-2, а вот путей всегда будет на порядок меньше 2^n-1, где n - это номер уровня дерева (корень в данных формулах считается первым уровнем). Так, если двоичное дерево, на Рисунке №48.1 считать конечным, то число узлов с вершинами у него 2⁶-1=63, число ребер 2⁶-2=62, а число путей 2^6-1=32. Если бесконечное дерево сделать десятичным, и каждое из ребер нумеровать десятичными цифрами, то число всех его возможных путей даст нам число всех возможных бесконечных десятичных дробей, что так же является континуумом (10^ℵ), ведь, как я еще раз напоминаю, 2^ℵ = n^ℵ = ℵ^ℵ = континуум.

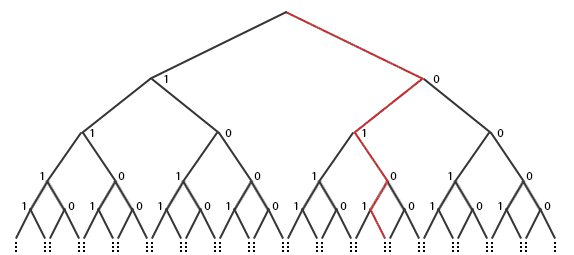
Вообще интересно посмотреть, что там с троичным, чеверичными и так далее... n-иными бесконечными деревьями. Ну, как мы выяснили, число путей в них так же будет равно континууму, а число вершин и ребер этого дерева будет так же счетно-бесконечным, но вот методы их сопоставления с натуральными числами будут отличаться. Так например, у троичного бесконечного дерева, вершины будем сопоставлять по формуле: N = (3^m-2×n+1)/2, а ребра по формуле N = (3^m+1-2×n-1)/2; у четверичного бесконечного дерева, вершины сопоставляются по формуле: N = (4^m-3×n+2)/3, а ребра по формуле N = (4^m+1-3×n-1)/3; и можно даже вывести универасльные формулы, которые подходят для любого k-ичного дерева, для вершин: N = (k^m-n×(k-1)+(k-2))/(k-1), для ребер: N = (k^m+1-n×(k-1)-1)/(k-1). Во всех этих формулах m - это так же уровень дерева, n - порядковый номер на уровне.

Даже если мы усложним наше дерево таким образом, что из корня и всех последующих вершин будет выходить бесконечное количество ребер, как схематично указано на Рисунке №48.3 (вашему воображению, так же остается лишь достроить бесконечность на каждом многоточии), то все равно у такого дерева количество вершин и ребер будет счетно-бесконечным. Однако для их идентификации, нам будет необходима аксиома выбора, поскольку на каждом уровне такого дерева требуется выбрать некое конкретное ребро и назначить его нулевым, тогда справа от него будут ребра отмеченные положительными натуральными числами, а слево отрицательными натуральными числами. Но для упрощения лучше выбрать другой способ нумерации, по-принципу чередования, пусть выбранное нами ребро будет первым, ребро справа от него вторым, ребро слева от него третьим, следующее справа четвертым, следующее слева пятым, и так далее. Мы уже делали нечто похожее, когда сопоставляли все целые числа с натуральными, сопоставив отрицательные с четными, а положительные с нечетными. Вообщем, используя аксиому выбора и чередующуюся нумерацию, мы сделали так что каждое конкретное ребро на каждому уровне будет иметь конкретный номер (n_k), ну а дальше все по тому же принципу, по которому мы расселяли инопланетян с бесконечно-вложенного корабля носителя в бесконечный отель. Для нумерации используем трансфинитные многочлены: ω^k×n_k-1+...+ω³×n₄+ω²×n₃+ω×n₂+n₁, а для сопоставления с натуральными числами метод факторизации простых чисел: N = 2^k₁×3^k₂×5^k₃×7^k₄×...×p_n^k_n. И все, доказательство того, что и в этом случае множество ребер будет бесконечным, готово. Тоже самое касается и вершин данного дерева. Ну а число путей, так же как и у деревьев с конечным количеством стволов на каждом уровне, будет равно континууму.

Теперь давайте представим еще более странные деревья, у которых нет начального корня. Примером может служить мультивселенная описываемая теорией космической инфляции, в которой бесконечные всленные бесконечно порождают другие вселенные и те, в свою очередь, делают тоже самое. То есть на мультивселенную можно смотерть как на бесконечный связанный неориентированный ациклический граф (бесконечное дерево с бесконечным ветвлением не имеющее корня), тогда отдельные вселенные будут вершинами данного графа. И даже в этом случае число вершин останется счетно-бесконечным. Дело в том, что в теории графов есть теорема, которая гласит, что каждый связный локально счетный бесконечный граф является счетным^[127]. Для начала разберем, что значит локально счетный бесконечный граф. Счетным бесконечным графом, называется такой граф, у которого счетное количество вершин и ребер. Под локально счетным графом здесь имеется в виду, что если мы из графа выделим любой отдельный подграф и он окажется счетным, то и весь граф окажется счетным. Ну а из бесконечного дерева, у которого нет начального корня всегда можны выделить поддерево, у которого будет начальный корень, более того, можно взять любую вершину, отбросить все что было сверху нее, и получится бесконечное дерево с корнем. И поскольку объединение счетного множества счетных множеств всегда счетно, то считаем теорему доказанной, а значит общее число вселенных в мультивсленной счетно-бесконечно. Однако стоит помнить, что поскольку квантовая механика может организовать материю конечным числом способов, то число видов вселенных будет и вовсе конечно, что мы и выяснили в первой главе, прийдя к выводу что в мультивсленной среди бесконечного множества вселенных обязательно встретятся абсолютно идеинтичные. Сам процесс рождения вселенных из пузырьков квантовой пены можно сопоставить с ребрами графа, следовательно их число тоже будет счетным. Но число путей в подобном графе так же останется несчетным континуумом.

Некоторые читатели от последнего примера могут остаться в недоумении. Разве мы не выяснили в примере с бесконечной вложенностью подразделений космических кораблей, что общее число пассажиров в таком бесконечно вложенном флоте, будет несчетно континуальным. А ведь флот так же можно интерпретировать как граф из последнего примера (бесконечное дерево с бесконечным ветвлением не имеющее корня). Ну да, действительно, пассажиров будет несчетное количество, но вот подразделений будет счетное множество. Если вам кажется это совершенно не интиутивным, то подумайте, а что такое пассажиры в интерпретации флота как графа. С подразделениями то все понятно это вершины графа, поэтому их число и должно быть счетным. Но пассажиры в нашем флоте подразумевались как конечная стадия бесконечной вложенности, а ведь у графа нет конечной стадии, он по определению бесконечный. Значит пассажиров в интерпритации графа следует рассматривать как все возможные пути графа. Если после такого объяснения вам стало немного яснее устройство континуума, то вы должны понять и следующий пример, который придумал сам Кантор, чтобы наглядно визуализировать континуум отдельными элементами.

Такое построение контнуума называется канторова пыль или кантрово множество^[128]. Чтобы создать его нужно взять отрезок, разделить его на 3 части и вырезать середину, с получившимися двумя отрезками сделать тоже самое, с получившимися четырмя отрезками снова делаем тоже самое, и так до бесконечности. Нетрудно посчитать, что каждый шаг (n) такой операции будет создавать 2ⁿ отрезков, сделав так бесконечное количество раз (ℵ), мы получим 2^ℵ отрезков - континуум. Многие так же могут возразить, что последнего этапа нет, ведь мы повторяем данную операцию бесконечно, однако если мы принимаем аксиому бесконечности, и считаем что множество натуральных чисел существует, значит должно существовать бесконечное количество таких операций, и тогда канторово множество тоже существует. Так вот каждая пылинка из кантрова множества так же сопоставляется со всем возможным множеством путей бесконечного двоичного дерева, потому что идентифицировать каждую пылинку можно только отследив всю историю деления отрезков, которая была бесконечной, и на каждом ее этапе мы выбираем в каком, правом или левом, из получившихся отрезков находится пылинка. Пылинки в канторовом множестве в итоге являются безразмерными точками, их число континуально, так же как число точек в изначальном отрезке. А значит, как бы ни парадоксально это выглядело, но в итоге всю эту безразмерную пыль можно будет сопоставить с точками в изначальном отрезке (при условии если мы будем соблюдать аксиому выбора). Но при этом с получившимися частицами канторовой пыли нельзя будет сопоставить комнаты из нашего отеля, потому множество частиц пыли окажется несчетным. По сути, канторова пыль, это один из первых примеров фрактала. Кантор данным примером, не только визуализировал континуум, но так же открыл для математиков дверь во фрактальную математику и теорию хаоса. Канторову пыль можно так же представить и в двух и в трех измерениях, см. рисунки ниже.

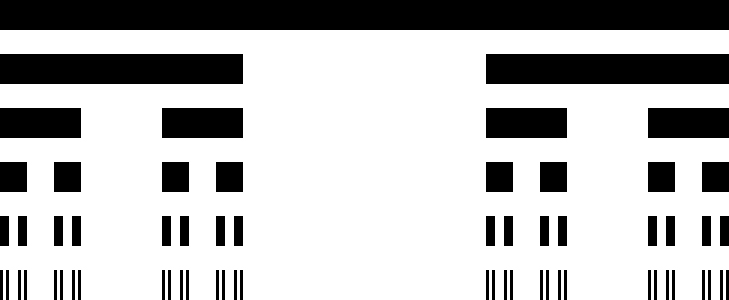
Канторова пыль из двухмерной проекции строится по принципу бесконечного четверичного дерева, каждый квадрат разбивается на девять равных частей, четыре угловые остаются, а остальные отбрасываются и так до бесконечности. Канторова пыль из трехмерной проекции строится по принципу бесконечного восьмеричного дерева, где уже каждый куб разбивается на 27 равных частей, 8 угловых остаются, а остальные отбрасываются. Можно создавать канторову пыль и из объектов большей размерности. Так канторова пыль из n-мерной проекции будет строиться по принципу бесконечного 2ⁿ-ичного дерева, где каждый n-мерный гиперкуб разбивается на 3ⁿ равных частей, 2ⁿ угловых частей остаются для дальнейшего разбиения, а остальные отбрасываются. Во всех случаях мы превращаем объекты любой размерности в безрамерные точки, и что самое поразительное, количество этих получившихся точек получается сопоставимо с количеством точек в изначальных объектах, таков этот удивительный континуум. Даже если мы возьмем объект с бесконечным количеством измерений, такие в физике не просто возможны, а явно существуют, например гильбертово пространство, в котором обитают и колеблются квантовые волны вероятности, то такой объект будет успешно преобразован в канторово множество, образовав канторову пыль. Кстати, как мы знаем, все промежуточные этапы такого деления будут счетны, ведь это будет подобно бесконечному древу с бесконечным ветвлением из Рисунка №48.3, следовательно, и все множество вселенных описываемых многомировой интерпретацией квантовой механики так же будет счетно. Поскольку тогда эволюция квантовой волны вероятности всей мультивселенной будет подобна бесконечномерному канторову фракталу, в котором версии вселенных, в которых могут произойти все возможные события не нарушающие законы квантовой механики, эквивалентны счетным промежуточным этапам дробления.

Существует ли вообще физический континуум, есть ли что-то по-настоящему несчетное в реальном мире. Этим вопросом задаются не только философы, но и физики. Казалось бы наше пространство и время должны быть континуальны, ведь физики часто используют термин пространственно-временной континуум. Однако тогда пространство-время должно позволять делить себя до бесконечности, потому что только так можно образовать континуум всех точек в пространстве и моментов во времени. А ведь мы знаем, что есть мельчайшие мастабы пространства и времени, это плансковская длина и планковское время. Но тут есть один важный момент они мельчайшие по принципу неопределенности квантовой механики, который физически не позволяет изучать что-либо меньшее. На таких масштабах согласно новейшим космологическим теориям пространство-время кипит и рождает новые вселенные в их собственные пространственные измерения, но это совсем не значит, что чего-то еще меньшего не существует^[129]. Некоторые физики считают что на меньших масштабах, чем планковские, пространство и время существуют но не в той форме, к которой мы привыкли^[130]. Другие уверены, что то что запрещает изучать принцип неопределенности следует признать не имеющим физического значения. Так или иначе, реален физический континуум или нет, это остается открытым вопросом, и возможно останется таким навсегда, потому что, как вы должны уже понимать, континуум не дает возможности описать все свои элементы. Не существует способа описать каждый счетный трансфинитный ординал, иначе множество всех этих чисел было бы счетно и не являлось континуумом, значит какие бы физические формулы для описания мира мы бы не выводили, охватить весь континуум, так чтобы можно было бы аргументировано заявить, что он лежит в основе всего, не получится. Но это совсем не запрещает строить модели для описания мира с его использованием. Например, математическая модель того же пространственно-временного континуума позволяет изучать теорию относительности и с очень большой точностью предсказывать результаты экспериментов и наблюдательных явлений.

Но давайте вернемся к рассмотрению континуума в математике и детальнее разберем почему континуум в объектах разной размерности получается одинаковым. Для начала соберем всю канторову пыль из одномерной проекции в один отрезок, и он окажется нулевого размера, но при этом по-прежнему будет содержать континуум точек внутри себя (2^ℵ/2^ℵ = 2^ℵ при соблюдении аксиомы выбора). Поразительное получается следствие, отрезок нулевой длины содержит столько же точек, как и любой другой отрезок. Хорошо, получается, как бы мы не уменьшали отрезок число точек в нем будет оcтаваться прежним, но так же легко показать, что как бы мы не увеличивали отрезок, число точек в нем не изменится и будет равно континууму. Прежде давайте отметим одну важную вещь, количество отрезков, которые содержатся внутри плоской фигуры столь же велико как и число точек внутри отрекза, просто мы изменили уровень измерения в рассуждении. Теперь давайте возьмем два отрезка разной длины и одну точку, точку расположим сверху, меньший отрезок по середине, а бо́льший отрезок снизу. Все это размещено на плоскости, а покуда на плоскости можно создать континуум линий, то из точки можно провести континуум лучей и все они в совокупности, так или иначе пройдут через все точки обоих отрезков

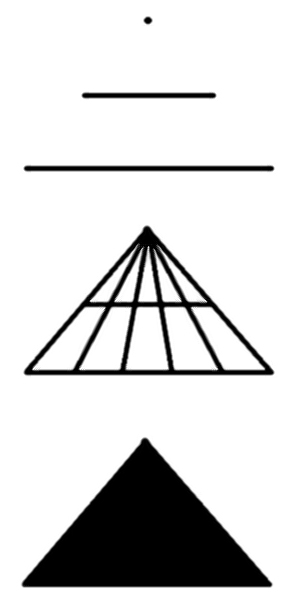
Хочется отметить, что если бы число линий было бы счетно, и проходили бы они, допустим, только через рациональные точки первого отрезка, например через половину (½), далее через четверть (¼) и три четвертые (¾), и так далее, то во-первых они бы не смогли покрыть весь отрезок, а во-вторых при продолжении их до второго отрезка они были бы уже разряжены. Счетная бесконечность отрезков проведенных из этой точки была бы похожа на бесконечно ветвящееся дерево из Рисунка №48.3, в котором между ветвями всегда было бы пространство. Однако континуум линий проведенных от этой точки до второго отрезка покрывает все точки обоих отрезков, показывая, что количество точек в них одинаково, но еще он так же показывает, что наша точка - отрезок нулевой длины тоже эквивалентна отрезкам (2^ℵ+2^ℵ = 2^ℵ-2^ℵ = 2^ℵ при соблюдении аксиомы выбора). А эквивалентность эта заключается в углах, под которыми линии входят в точку, и количество возможных углов так же континуально, как и количество точек в отрезке. Аксиома выбора очень важна при постоении такой сполшной плотности линий, поскольку утверждение "мы можем взять любую точку на отрезке и провести через нее линию" не имеет смысла без аксиомы выбора.

Вообще континуум очень сложно изменить, мы можем разбить его на счетные подмножества, но в каждом из подмножеств континуум останется все тем же. Но и увеличить в размерах его тоже не просто, что бы мы с ним не пытались сделать, он останется континуумом. Теперь давайте убедимся как континуум точек на плоскости или континуум точек в объеме легко превратить в континуум точек в отрезке. Для начала давайте возьмем прямоугольник и отрезок имеющий ту же длину. Каждая точка внутри прямоугольника будет иметь какую-то координату. Возьмем для примера некие трансцендентные координаты: x = 0,212347...; y = 0,312486... и сделаем из них единую координату x, просто расставив цифры в порядке чередования:
0,2ø1ø2ø3ø4ø7ø...
0,ø3ø1ø2ø4ø8ø6...
0,231122344876...
Получилась координата x = 0,231122344876..., отметим ее на отрезке. Так всевозможные координаты x и y можно превратить в координаты только по x, и превратить все множество точек прямоугольника в отрезок. Теперь давайте то же проделаем с кубом, пусть его длина так же соотвествует длине отрезка. Так же возьмем для примера координаты некой трансцендентной точки внутри куба: x = 0,718365...; y = 0,226481...; z = 0,496574... и сделаем из них единую координату x, так же расставив цифры в порядке чередования:
0,7øø1øø8øø3øø6øø5øø...
0,ø2øø2øø6øø4øø8øø1ø...
0,øø4øø9øø6øø5øø7øø4...
0,724829866345687514...
Получилась координата x = 0,724829866345687514..., отметим ее на отрезке. Отсюда, аналогично следует вывод, что все точки куба можно превратить в точки отрезка. В более общем смысле точки пространства любой счетной размерности, можно превратить в точки отрезка ((2^ℵ)² = (2^ℵ)³ = (2^ℵ)ⁿ = 2^ℵ) при соблюдении аксиомы выбора, где n - натуральное число или счетный ординал), и как мы показали точки этого отрезка можно превратить в точки отрезка любой длины, в том числе и нулевой (точку). Получается, что математика позволяет свернуть все бесконечное пространство в одну точку. У многих от этого уже вероятно идет кругом голова. Все кажется каким-то неправильным, неинтуитивным, противоречащим здравому смыслу, а мы с вами всего лишь выводим принципы геометрии из теории множеств. Так же казалось и математикам-современникам Кантора, за что его теория изначально и была встречена в штыки. Однако уже спустя несколько десятков лет именно благодаря теории множеств математика испытала колоссальное развитие во всех областях. Кроме того появилось много новых областей, в частности топология, которая изучает как раз те самые свойства превращения размерностей, размеров и форм континуума. Развитие математики послужило толчком к развитию других точных наук и всего научно-технического прогресса.

Перед тем как идти дальше, давайте разберем другие виды чисел, которые встречаются в математике. Проверим может ли совокупность каких-нибудь других видов чисел быть больше континуума. Заранее разочарую вас, найти числа, множество которых будет больше континуума нам не удастся, но мы обнаружим, как все эти числа окажутся напрямую связаны с разными геометрическими расширениями континуума. Но прежде я должен сказать, что кое-что не договорил, когда рассказывал про неизвлекаемые корни. Тогда я имел ввиду не все виды неизвлекаемых корней, а только те, которые создают иррациональные числа, и в этот класс я не включил корни вроде √-1. На первый взгляд, выражение √-1 бессмысленно, так как не существует такого числа, которое умноженное само на себя давало бы минус единицу. Но математики предположили, что такое число существует и назвали его мнимая единица: i² = -1. А все числа, которые включают в себя мнимую единицу, называют комплексными (C), например: 3+4×i или 6-2×i. Зачем же математикам понадобились такие, казалось бы, ненастоящие числа. Ну во-первых, эти числа позволяют правильно решать степенные уравнения, потому что часть решений степенных уравнений получаются комплексными, а значит счетное подмножество комплесных чисел, что могут получится при решении степенных уравнений, являются частью множества алгебраических чисел. Так что, если быть более точным, то на диаграмме в Рисунке №44 я изобразил только действительные алгебрачиеские числа, поскольку комплесные алгебраические числа, естественно не являются действительными.

А еще комплексные числа позволяют легко превратить линию в плоскость. Поле действительных чисел (R), как многие возможно помнят из алгебры, представляет собой линию, или как ее принято называть числовую ось, где каждое число это какая-то точка на этой оси. Комплексные числа добавляют еще одно измерение, так называемую мнимую ось, которая откладывается перпендикулярно действительной оси, и поле комплексных чисел представляет из себя плоскость, например: число 3+4×i соответствует точке на этой плоскости с координатами x = 3, y = 4, а число 6-2×i соответствует точке на этой плоскости с координатами x = 6, y = -2. Как вы наверное догадались, комплексные числа нельзя сравнивать, потому что они включают в себя численные части из разных измерений, и например, бессмысленно спрашивать что больше 2×i+3 или 3×i+2. Изучение отношений действительных чисел называется стандартным анализом, а изучение отношений комплексных чисел называется комплексным анализом, это огромные разделы математики, которые как и всякие другие разделы легко выводятся из теории множеств. Ну а как мы выяснили, используя аксиому выбора в теории множеств, плоскость можно легко превратить в линию (R² = R), значит и комплексные числа можно сопоставить с действительными, и количество всех комплексных чисел так же равно континууму ((2^ℵ)² = 2^ℵ).

Можно расширять поле комплексных чисел, добавляя туда новые мнимые единицы, при этом будет увеличиваться количество измерений. Однако чтобы математика хорошо работала число измерений должно быть равно 2ⁿ, хотя необязательно пользоваться всеми измерениями. Сейчас поясню, что это значит. Следующее расширение комплексных чисел называется кватернионами (H). Мы добавляем еще две мнимые единицы j и k, так чтобы выполнялись следующие правила: k² = j² = i² = -1 и k×j×i = -1, но k ≠ j ≠ i. Именно четыре вида единиц (одна реальная и три мнимые) позволяют создать работающую взаимную таблицу умножения. Если нам необходимо отобразить лишь три измерения, то одну мнимую единцу можно не использовать. Например, число 2+9×i-7×j соответствует точке в пространстве с координатами x = 2, y = 9, z = -7. Однако в физике часто задействуют все три мнимые единицы, потому что на самом деле мы живем в четырехмерном пространстве и время это четвертое измерение, так например, число 8-6×i-3×j+5×k соответствует точке в пространстве с координатами x = 8, y = -3, z = 5 и моменту времени t = 5. Кватернионы используются в теории относительности для изучения свойств нашей вселенной, по сути именно Эйнштейн ввел термин пространственно-временной континуум, который как следует из аксиомы выбора можно сопоставить с линией (R⁴ = R), а значит множество всех кватернионов, так же как множество всех комплексных чисел можно сопоставить с множеством всех действительных чисел  и оно так же соответствует континууму ((2^ℵ)⁴ = 2^ℵ).

Можно и дальше продолжать добавлять мнимые единицы, но их количество должно соответствовать 2ⁿ-1 (минус один, потому что помимо мнимых у нас всегда есть реальная единица), чтобы с ними могла работать алгебра и правильно выполнялись математически операции. Хотя все же с добавлением мнимых единиц алгебра становится более сложной, например уже для кватернионов не выполняется коммунитативность умножения, или говоря простыми словами, от перестановки множителей результат операции изменится: a×b ≠ b×a. Числа, которые содержат в себе семь мнимых единиц, таких что o² = n² = m² = l² = k² = j² = i² = -1 и o×n×m×l×k×j×i = -1, но o ≠ n ≠ m ≠ l ≠ k ≠ j ≠ i, и могут описывать пространства вплоть до восьмимерных, называются октонионами (O), для них уже не работает ассоциативность умножения, то есть правило порядка вычисления с тремя разными множителями: (a×b)×c ≠ a×(b×c). Следующее расширение, называется седенионами (S), такие числа как нетрудно посчитать из формулы могут содержать в себе до 15 мнимых единиц, таких что w² = v² = u² = t² = s² = r² = q² = p² = o² = n² = m² = l² = k² = j² = i² = -1 и w×v×u×t×s×r×q×p×o×n×m×l×k×j×i = -1, но w ≠ v ≠ u ≠ t ≠ s ≠ r ≠ q ≠ p ≠ o ≠ n ≠ m ≠ l ≠ k ≠ j ≠ i, и могут описывать пространства вплоть до шестнадцатимерных, для них уже не работает даже альтернативность умножения, то есть правило порядка вычисления с двумя разными из трех множителей: (a×a)×b ≠ a×(a×b), однако работает степенно-ассоциативность, то есть правило порядка вычисления с тремя одинаковыми множителями: (a×a)×a = a×(a×a), но возникают так называемые делители нуля, то есть, это такие числа (b), разделив ноль на которые (0/b = a), получится число не равное нулю (a ≠ 0)^[131]. Все эти ограничения в алгебре не дают полноценно работать c многомерными комплесными пространствами, но все же это хоть какая-то возможность изучать континуум. Многомерные пространcтва используются для изучения моделей физических полей в квантовой механике, это позволяет моделировать все странности, что происходят в микромире элементарных частиц и кажутся на первый взгляд неподвластны здравому смылу, но математика более или менее справляется с описанием этих процессов. Но как я уже говорил, для полного изучения квантовой механики в математических моделях иногда требуется вводить пространство с бесконечным числом измерений, соотвественно для его описания нам потребовалась бы система с бесконечным количеством мнимых единиц. Мы уже знаем, что такие системы называются гильбертовым пространством. И как мы уже выяснили, количество точек в таком пространстве с бесконечным количеством измерений ничем не отличается от количества точек в пространстве любой другой размерности (R^N = R), значит и числа которые могут содержать в себе бесконечное количество мнимых единиц можно сопоставить с действительными числами, и количественно мы так и не выбрались за пределы континуума ((2^ℵ)^ℵ = 2^ℵ).

Однако все мнимые единицы (их называют элиптическими), которые мы вводили выше, создают только Евклидовые пространства, то есть неискривленные. Но мы знаем, что бывают еще искривленные пространства. Можно ввести другой вид мнимых единиц, которые создадут иные пространства. Например, представим себе мнимую единицу (гиперболическую), такую что i_h² = 1 и i_h ≠ 1 ≠ -1, тогда плоскость комплексных чисел будет обладать свойствами геометрии Лобачевского. Аналогично ее можно расширить другими мнимыми единицами с таким же свойством до большего числа измерений, создавая многомерные пространства с отрицательной кривизной^[132]. А если мы введем такую мнимую единицу (параболическую), что i_p² = 0 и i_p ≠ 0, тогда плоскость комплексных чисел будет обладать свойствами геометрии Римана, а расширив ее другими такими же мнимыми единицами мы получим многомерные пространства с положительной кривизной^[133]. Алгебра подобоных систем тоже будет обладать рядом дефектов, в частности все они будут иметь делители нуля. Иногда элиптические, гиперболические и параболические мнимые единицы комбинируют, создавая разнообразные системы чисел, чтобы изучать всякие геометические преобразования или движения, например искривление пространства в общей теории относительности, обычно все такие системы называют гиперкомплексными числами. И сколько бы видов мнимых единиц мы не вводили, вся совокупность создаваемых гиперкомплексных чисел количественно не сможет превысить континуум, потому что, в соотвествии с аксимой выбора, континуум можно транслировать на любую размерность и любой вид геометрии. В целом же континуум получается настолько большой, что не только множество всех действительных чисел, но и совокупность всех чисел, которыми сегодня пользуются математики, не будет больше континуума.

Ну а поскольку объекты в геометриях с разной кривизиной могут быть превращены друг в друга или одинаково стерты в канторову пыль, то есть они содержат одинаково континуальное множество точек, то получается что не только число всех возможных прямых на плоскости будет континуально-бесконечным, но и число всех возможных кривых на на плоскости будет континуально-бесконечным. И так же как число всех возможных плоскостей в пространстве будет континуально-бесконечным, так же и число всех возможных искривленных поверхностей в пространстве тоже будет континуально-бесконечным. И так далее, аналогично, для любых n-мерных и в том числе бесконечномерных пространств. Чтобы подробно доказать почему в пространстве любой размерности количество всех видов криволинейных объектов столь же велико как количество всех видов прямолинейных объектов и количество всех точек нужно обратиться к более серьезному математическому анализу, что проходят уже в ВУЗах. Доказательство будет базироваться на понятии непрерывной функции, что является краеугольным камнем всего математического анализа^[134]. В его дебри пределов и окрестностей мы конечно не полезем, но если совсем вкратце, то непрерывная функцая, это по сути и есть непрерывная кривая (или прямая). Ну или если быть точным, то любая кривая или прямая (и в том числе любой n-мерный прямолинейный или криволинейный объект) это непрерывная функция определенная на действительных (R) или комплексных числах (R^N) и соотвествующая действительным (R) или комплексным числам (R^N). Так же у любой непрерывной линии две близлежащие точки бесконечно близки, и отличить их у разных кривых можно только по их производной, ну а производные можно рассматривать как углы наклона, которые так же континуальны и измеряются в действительных (R) или комплексных числах (R^N). Так что множество всех таких функций можно соотнести с континуальным количеством континуальных множеств. И как счетное количество счетных множеств было счетно, так же и континуальное количество континуальных множеств континуально. Последнее звучит почти как скороговорка, но на самом деле это скорее притча, о том что континуум тоже не так то просто увеличить.

Концептуальный переворот совершенный Кантором в математике просто неоценим, на языке его теории множеств можно описать любую математическую систему, но осталась в этой теории одна задачка, которую он сам не решил, и которая до сих пор является предметов активных споров среди математиков. Для понимания этой задачи вначале еще раз вспомним что такое кардинальность множества (иногда можно встретить термин "мощность множества", что значит тоже самое). Мы с этим понятием уже сталкивались. Кардинальность - это количественная характеристика множества. Для конечного числа кардинальность равна самому этому числу, например |5| = 5. Для любого трансфинитного счетного ординала кардинальность равна счетной бесконечности |ω+5| = |ω×5| = |ω⁵| = ℵ. Так же мы с вами выяснили, что кардинальность множества всех натуральных чисел равна кардинальности множества всех целых чисел, равна кардинальности множества всех рациональных чисел, равна кардинальности множества всех алгебраических чисел и равна счетной бесконечности: |N| = |Z| = |Q| = |A| = ℵ. А вот кардинальность множества действительных чисел (так же как и всех видов комплексных чисел) равна континууму: |S| = |O| = |H| = |R| = 2^ℵ, который является булеаном счетной бесконечности. Вопрос, которым задался Кантор звучал следующим образом, а есть ли кардинальности между ℵ и 2^ℵ. Гипотеза которую он выдвинул, предполагает, что между ℵ и 2^ℵ, нет других кардинальностей. То есть, если расположить всевозможные кардиналы в порядке возрастания, то получится: "1,2,3,4,5,...,ℵ,2^ℵ,...". Это предположение называют континуум-гипотезой^[135].

Ну пусть между счетной бесконечностью и континумом может не быть других кардиналов, но что на счет кардиналов бо́льших континуума. А вот в существовании таких кардиналов Кантор был уверен, благодаря другой своей теореме, которая доказывала, что любое множество и множество всех подмножеств этого множества не могут иметь одинаковую кардинальность, и множество всех подмножеств всегда будет количественно больше исходного^[112]. Получается, операция булеана 2ⁿ, определенная на количественных бесконечностях будет порождать все бо́льшие кардиналы. Поэтому мы можем легко показать, что существуют кардиналы бо́льшие чем континуум, взять хотя бы булеан континуума: 2^2ℵ = ℵ^ℵℵ = (2^ℵ)^2ℵ - множество всех подмножеств действительных чисел. Такое бесконечное количество тоже будет несчетным, но будет больше континуума 2^ℵ < 2^2ℵ. Это настолько много, что для описания всех его элементов уже никаких видов чисел не хватит. Иногда в теории множеств вместо классической записи булеана как 2ⁿ, используется запись P(n), являющаяся сокращением от Powerset(n), что переводится соотвественно как множество всех подмножеств. Поэтому иногда можно увидеть, что континуум обозначают так P(ℵ), а булеан континуума так P(P(ℵ)). Как же нам представить булеан континуума, если он даже не может быть выражен всеми видами чисел, которые мы можем вообразить. Ну из его свойств, по определению, получается что булеан континуума (2^ℵ)^2ℵ - эквивалентен множеству всех возможных функций, которые могут быть заданы на континууме (R^R). То есть, если объяснять более наглядно, то булеан континуума соответствует всем возможным кобминациям точек в пространстве любой размерности. Это легко доказывается в комбинаторике формулой числа размещений с повторениями. Но если нужны более подробные разъяснения, то представьте себе пространство любой размерности (неважно линию, плоскость, объем или что-то более многомерное), в любом таком пространстве, даже если оно конечно и ограничено, потенциально может содержаться континуум безразмерных точек. И мы можем распределить эти безразмерные точки, по двум принципам: ставить точку или не ставить точку, а значит число всех возможных комбинаций будет равно 2^{континуум} = 2^2ℵ. Еще раз подчеркну, что это должны быть всевозможные комбинации, потому что если хоть как-то ограничить возможность комбинирования, то булеан не получится, а значит число комбинаций будет просто континуально 2^ℵ. Примером ограниченного комбинирования может служить множество всех возможных непрерывных функций (множество всех возможных кривых). Все непрерывные функции, так же заданы на континууме (R^R), но поскольку у любой непрерывной линии две близлежащие точки бесконечно близки, то мы не можем говорить о всех возможных комбинациях расположения этих точек относительно друг друга.

И поскольку уже нет смысла вводить новые виды чисел (все равно они, даже будучи представлены в бесконечном виде, как например трансцендентные числа, не способны дать нам совокупность сопоставимую с булеаном континуума), то стоит попробовать как-то визуализировать всю совокупность функций заданых на действительных числах. Для этого обратимся к основам математической логики. Нас интересуют логические функции, для упрощения будем называть их суждениями. Математическая логика упрощает все возможные высказывания до двух: "правда" и "ложь", или "да" и "нет", или условно 1 и 0. Суждение работает с высказываниями и делает вывод. Теперь очень важный момент, так получается, что если какие-то суждения работают c n-ным количеством высказываний, то мы имеем 2ⁿ вариантов рассуждения для каждого суждения, и 2²ⁿ видов таких суждений^[136]. И чтобы было понятней, давайте разберем простейший пример. Допустим суждение работает только с одним высказываением (n=1), это высказывание может быть либо верно либо нет, значит у нас будет 2¹=2 вариантов рассуждения. Тогда получается, что видов суждений должно быть 2²¹=4. Проверим так ли это. Во-первых мы можем соглашаться с высказыванием и делать вывод "правда" или "ложь", в зависимости от самого высказывания. Во-вторых мы можем не соглашаться с высказыванием, отрицая его, и делать вывод "ложь" если высказывание утверждает "правду", или наоборот делать вывод "правда" если высказывание утверждает "ложь". В-третьих мы можем слепо верить во что-то, и если высказывание подверждает это, то соглашаться с ним, а если не подверждает все равно утверждать что это "правда". В-четверых мы можем слепо не верить во что-то, и соглашаться с высказыванием, если оно это отрицает, но если высказывание это подверждает, то все равно его отрицать. Все эти суждения можно представить в виде таблицы, изображенной на Рисунке №52.1, такие таблицы в математической логике принято называть таблицами истинности. Это правило можно проверить и на суждениях с двумя высказываниями (n=2), тогда очевидно вариантов рассуждений для каждого суждения будет 2²=4, когда либо оба высказывания верны, либо оба неверны, либо верно только первое, либо верно только второе. Ну в соответствии с правилом, получается, что число видов таких суждений должно быть равно 2²²=16, и чтобы проверить так ли это, сверьтесь с таблицей из Рисунка №52.2.

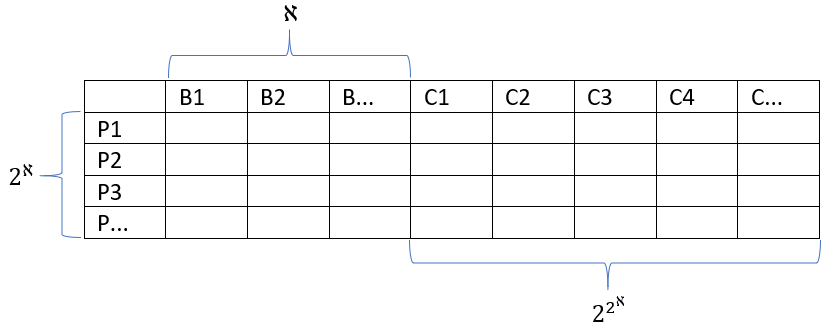
Понятно, что чем больше высказываний, тем больше возможности их скомбинировать, чтобы выстроить рассуждение, и тем еще больше видов суждений можно получить. Например, уже для 5 одновременных высказываний, мы получаем 2⁵ = 32 их возможных комбинаций для последующих рассуждений, а число видов таких суждений и вовсе будет 2²⁵ = 4294967296. Так что известная поговорка "сколько людей столько мнений", не совсем верна, мнений может быть намного больше. Но так или иначе для конечного числа высказываний мы имеем конечное число их комбинаций и конечное число возможных суждений. Но я думаю вы уже поняли к чему я все это веду, если количество высказываний становится бесконечным (ℵ), то количество их комбинаций для рассуждений будет равно континууму (2^ℵ), а количество возможных суждений будет равно булеану континуума (2^2ℵ). Это интресный вывод, который имеет важные философские следствия, получается что если бы человек мог знать бесконечное количество фактов, число возможных мнений об этих фактах, которое бы он мог сложить в голове, было бы больше континуума. Но если вернуться, к тому для чего мы влезли в математическую логику, а именно к визуализации всех возможных функций на действительных числах, то они как раз сопоставляются со всеми возможными логическими функциями на бесконечном числе высказываний. Вспомним, что любое действительное число (неважно рациональное или иррациональное) можно закодировать в бесконечном количестве бит, то есть как некую бесконечную последовательность нулей и единиц. Значит любое действительное число в такой интерпритации можно трактовать как бесконечное число высказываний. Ну тогда можно считать доказанным, что число всех возможных суждений на бесконечном числе высказываний соответствует всем возможным функциям на действительных числах.

И теперь, раз мы уверены, что булеан континуума соответствует всем возможным комбинациям точек на линии, или на плоскости или в пространстве любой размерности, то используя аксиому выбора, можно транслировать булеан континуума на другие похожие ситуации. Так множество всех комбинаций прямых или кривых на плоскости или в пространстве любой размерности тоже будет равно булеану континуума, так же как множество всех комбинаций всех видов объемных тел с учетом возможности наложения друг на друга в пространстве любой размерности. Кроме того мы можем размещать точки в пространстве не только по принципу ставить не ставить (или по принципу белая, черная, что одно и тоже), но и раскрашивать их в разные цвета. И сколько бы возможных цветов мы не использовали, пусть даже целый континуум вариантов оттенков, все равно число возможных комбинаций таких раскрашенных точек не будет превышать булеан континуума, потому что 2^2ℵ = n^2ℵ = ℵ^2ℵ = (2^ℵ)^2ℵ= ℵ^ℵℵ. Получается, что булеан контнинуума можно представить еще как всевозможные виды раскраски пространственного континуума (хотя надо понимать, что это математическая абстракция, и с физической точки зрения это не так, потому что мы не можем красить сколь угодно малые масштабы).

Однако для теории множеств булеан котинуума не предел, потому что мы можем продолжать и дальше создавать множество всех подмножеств, создав таким образом, булеан булеана континуума 2^22ℵ = ℵ^ℵℵℵ = (2^2ℵ)^22ℵ = P(P(P(ℵ))) - это уже не поддается никакой визуализации, на сегодняшний день неизвестна ни одна совокупность абстрактных объектов, которая представляла бы собой булеан булеана континуума. То есть, 2^22ℵ не имеет никаких соответствий, даже если попытаться описать с помощью него всевозможные абстрактные понятия. Ведь мы выяснили, что все возможные бесконечные абстрактные суждения уже ограничены 2^2ℵ. Поэтому ничто известное человечеству не составляет такую бесконечность, как 2^22ℵ, она не имеет никаких аналогий не только в реальности, но и в абстракции. Однако, согласно аксиоме множества всех подмножеств, у любого множества существует булеан, значит 2^22ℵ существует, так же как существует 2^222ℵ и так далее, каждый количественно больше предыдущего. Более смелое предположение Кантора состояло в том, что и между этими булеанами от булеанов несчетной бесконечности тоже нет промежуточных кардиналов, и если более полно расположить всевозможные кардиналы в порядке возрастания, то получится: "1,2,3,4,5,...,ℵ,2^ℵ,2^2ℵ,2^22ℵ,2^222ℵ,..." Это предположение называют обобщенной континуум-гипотезой^[135].

Однако, как оказалось, показать, что промежуточные кардиналы не существуют, или что они наоборот существуют, невозможно. В 1940 Гедель доказал, что континуум-гипотезу невозможно опровергнуть в ZFC^[137]. В 1963 году другой математик Пауль Коэн доказал, что континуум-гипотезу так же невозможно и доказать в ZFC, и сделал вывод что в рамках ZFC континуум-гипотеза независима от ее аксиом. То есть работа Коэна показала, что континуум-гипотеза не может быть даже теоремой ZFC, потому что в принципе не выводится из аксиом ZFC, мы можем лишь принимать или не принимать ее как дополнительную аксиому. Тогда у нас получится две теории множеств: ZFC где континуум-гипотеза верна, и ZFC где континуум-гипотеза не верна, причем ни одна из них не хуже другой, обе будут вплоне рабочие, и так же на основе каждой можно будет вывести все остальные разделы математики^[138]. В 1999 году Соломон Феферман тоже показал, что континуум-гипотеза останется независимой, даже если мы добавим к ZFC другие аксомы связанные с кардиналами (например постулирующие существование сверхбольших кардиналов)^[139]. Получается что проверка континуум-гипотезы лежит за пределами общепринятых аксиом теории множеств. Я не буду приводить все вышеперечисленные доказательства, они слишком сложны и упрощенно объяснить их не получится и читатель в любом случае пока не сможет уловить суть доказательств, особенно, если он еще даже не знаком с теорией моделей. Скажу только, что камнем преткновения является аксиома выбора, ее принятие делает континуум-гипотезу незасивимой, но ее явное отрицание вообще не дает возможности корректно работать с континуум-гипотезой. Все те же самые выводы справделивы как для простой континуум-гипотезы, так и для ее обобщенной версии.

Давайте лучше посмотрим на некоторые сложности и парадоксы, с которыми можно столнкуться, работая с континуум-гипотезой. Для начала кардинал счетной бесчонечности (ℵ) будем записывать так ℵ₀, а следующий за ним кардинал запишем ℵ₁. Что же такое ℵ₁? Во-первых ℵ₁ должен быть несчетным, ведь раз ℵ₁ - следующий кардинал после ℵ₀, значит ℵ₀ < ℵ₁, то есть он несопоставим со счетной бесконечностью и его нельзя заселить в бесконечный отель Гильберта. Чтобы понять природу ℵ₁ вернемся к ординалам. Мы убедились, что кардинальность любого счетного ординала, какие бы рекурсии над ним не создавались будет равна ℵ₀, потому количественная характеристика у всех них равняется обычной бесконечности, такой же как бесконечность из обычных натуральных чисел. Но чему будет равна кардинальность множества всех возможных счетных ординалов {1,2,3,4,...ω,ω+1,ω+2,...ω×2,...ω²,...ω^ω,...}. Представляю вам ω₁ - это первый несчетный ординал, который следует сразу за всеми счетными ординалами. Согласно аксиоме выбора любое множество можно упорядочить, значит любому множеству можно сопоставить порядковое число, если не хватит конечных чисел можно воспользоваться трансфинитными ординалами. Значит, в соотвествии с аксиомой выбора ω₁ существует - это ординал, который упорядочивает множество всех счетных ординалов, то есть идет сразу после. Ну а если он не входит в множество счетных ординалов, значит он не является счетным, а поскольку он первый несчетный, то его кардинальность будет равна первому кардиналу после ℵ₀, то есть |ω₁| = ℵ₁. Получается, что первый трансфинитный ординал соотвествующий ℵ₀, следовало бы записывать ω₀, но почти всегда ноль в записи опускают и пишут просто ω, однако первый трансфинитный кардинал, напротив, всегда пишут с нулем - ℵ₀.

Теперь давайте попробуем изобразить несчетный ординал ω₁, так же как до этого изображали счетные вроде ω или ω×2. Мы не можем взять для иллюстрации счетную бесконечность, ведь добавив палочку к любой счетной бесконечности мы снова получим счетную бесконечность: ℵ+1 = ℵ. Тогда давайте представим несчетную бесконечность, например обычный отрезок состоящий из несчетного числа точек и попробуем на нем найти ω₁. То что, точки на линии не поддаются счету не означает, что у них отсутствует порядок, отнюдь, они следуют одна за другой, однако в отличие от тех рисунков выше, где я демонстрировал счетные ординалы, мы не можем обозначить произовольную точку на отрезке, так чтобы ей присвоить какой-либо счетный ординал. Задумайтесь, где на этом отрезке будет точка под номером 1, то есть следующая сразу за 0? А где будет точка под номером ω, ω+1, ω×2 или под номером ω^ωω...? Отвечаю: все они будут бесконечно близки к 0. Но это не все, мы выяснили, что аксиома выбора позволяет свернуть весь континуум в одну точку, а значит все ординалы, кардинальность которых меньше или равна 2^ℵ₀ тоже будут находится в этой точке. Значит, такие ординалы как ω₁, ω₁+1, ω₁×2 и т.п., имеющие кардинальность: |ω₁| = |ω₁+1| = |ω₁×2| = ℵ₁, тоже окажутся в этой точке. Аксиома выбора просто не дает нам сдвинутся с точки, в которой начинается отрезок. Теперь вводим ω₂ - это ординал, который идет сразу после всех ординалов, имеющих кардинальность ℵ₁, так вот аксиома выбора не позволяет показать, что ω₂ лежит на отрезке (что было бы опровержением континуум-гипотезы), но и то что мы его там не обнаружим (что было бы доказательством континуум-гипотезы) так же невозможно показать, пока мы придерживаемся аксиомы выбора. Давайте подумаем, если континуум-гипотеза верна ((|ω₂| > 2^ℵ₀), то где должен находится ω₂. Он не может находится на отрезке поскольку должен лежать за пределами континуума точек, а где эти пределы, если в соответствии с аксиомой выбора отрезок можно увеличить до любых размеров и в нем по-прежнему будет континуум точек, можно увеличить размерность отрезка сделав его плоскостью, объемом или любым n-мерным пространством, но опять же в соответствии с аксиомой выбора в этом n-мерным пространстве по-прежнему будет содержаться континуум точек. С аксиомой выбора попросту невозможно описать пределы, где тогда будет находится ω₂. Теперь давайте представим, что если континуум-гипотеза неверна (|ω₂| < 2^ℵ₀), и значит ω₂ лежит на отрезке, то где он будет. Получается, что ω₂ так же будет находится в нулевой точке, ведь в соответствии с аксиомой выбора континуум можно свернуть до нулевого размера, там же тогда будет и ω₃ ведь к нему применима та же логика, там же будет любой ω_n, ибо мы можем продолжать сворачивать континуум снова и снова, оставаясь в одной точке. Тогда аксиома выбора не даст описать такой ω_n, который будет лежать за пределами континуума, значит опровержение континуум-гипотезы лежит за пределами возможностей ZFC. Континуум-гипотеза и есть, одно из тех выражений, которые в соответстивии с Теоремой Геделя о неполноте ограничивают силу современной теории множеств. Континуум-гипотеза сыграла злую шутку со своим создателем, безуcпешные попытки Кантора доказать ее или опровергнуть, вдобавок с постоянной критикой его идей со стороны других математиков, свели его с ума. Он часто лечился в психиатрических лечебницах и в конце-концов отошел от математики. Но даже неразрешенные задачи оставленные Кантором оказали огромное влияние на современную математику, отчасти именно в попытках разрешить парадокс континуум-гипотезы Геделем и была создана его Теорема о неполноте, совершившая другой переворот в мире математики.

Что ж, если континуум-гипотеза неразрешима при использовании аксиомы выбора, может тогда стоит от этой аксиомы отказаться и заменить ее какой-нибудь другой. Но на самом деле для нее нет полноценной замены поскольку, она нужна для многих разделов математики (больше всего при отказе от аксиомы пострадает математический анализ, большинство его определений от которых отталкиваются его теоремы попросту перестанут работать), без нее теория множеств обеднеет как универсальный инструмент способный связывать все разделы математики. Справедливости ради, стоит отметить, что существуют и другие системы аксиом теории множеств, как без аксиомы выбора, так и с другими аксиомами, которые пытаются взять на себя часть ее функций, в которых континум-гипотеза может быть как верна, так и неверна, в зависимости от системы аксиом. Они так же не хуже и не лучше ZFC, просто так же как и в разных системах аксиом геометрии, у них свои границы применимости.

Но раз такая чехарда творится с этой континуум-гипотезой, как же нам тогда сформулировать арифметику кардиналов. Для этих целей помимо кардиналов обознаемых еврейской бувой Алеф (ℵ), вводятся кардиналы, которые обозначаются еврейской букой Бет (ב). Они и будут символизировать все эти булеаны бесконечных множеств: ℵ₀ = ב₀, 2^ℵ₀ = ב₁, 2^2ℵ₀ = ב₂, 2^22ℵ₀ = ב₃, и так далее, тогда алефы будут символизировать количественные характеристики множества ординалов: ℵ₀=|множество всех конечных чисел|,  ℵ₁=|множество всех счетных ординалов, идущих после конечных чисел|, ℵ₂=|множество всех несчетных ординалов, идущих после счетных ординалов, идущих после конечных чисел|, ℵ₃=|множество всех несчетных ординалов, идущих после несчетных ординалов, идущих после счетных ординалов, идущих после конечных чисел|, и т.д. В ZFC нельзя показать как именно связаны ℵ-кардиналы и ב-кардиналы, просто придется принять существование обоих видов. Тогда общие правила арифметики трансфинитных кардиналов будут выглядеть так:

Подробные пояснения к приложению давать не буду, в нем в более формальном виде я изложил все, что и так уже рассказывал. Остановится можно разве что на высших арифметических действиях над кардиналами. Если тетрация еще имеет смысл, только в случае, если мы используем конечные числа в качестве показателя: ²ℵ₀ = ℵ₀^ℵ₀ = ב_1, ³ℵ₀ = ℵ₀^ℵ₀ℵ₀ = ב_2, ⁿℵ₀ = ב_n-1 (размер получаемого кардинала зависит именно от высоты степенной башни), то выражение ^ℵ₀ℵ₀ уже не имеет никакого смысла, потому что тетрация символизирует порядок возведения в степень (для операции возведения в степень не работает закон произвольных перестановок и произвольного порядка действий, как у сложения и умножения, то есть: a^b ≠ b^a и (a^a)^a ≠ a^(aa), а значит a^aa... считается с конца, и только по порядку), но ℵ₀ не является порядковым числом, это кардинал - количественная характеристика, поэтому выражение ^ℵ₀ℵ₀ считается неопределенным. Ну и как следствие все высшие действия над кардиналами получается тоже не имеют смысла, ведь по определению: ^ℵ₀ℵ₀ = ℵ₀[4]ℵ₀ = ℵ₀[5]2, что делает неприменимым уже пентацию. Однако мы еще можем записать такое выражение ^ωℵ₀, что означает бесконечную степенную башню ℵ₀^{ℵ₀ℵ₀...} = ב_ω (поскольку ω - трансфинитный ординал, то есть порядковое число, то никаких противоречий нет). Так как на каждом этаже будет происходить ℵ₀^ב_n = ב_n+1, то в случае с бесконечным числом этажей это и даст нам ב_ω. Однако выражение ^ω+1ℵ₀ не позволит нам получить ב_ω+1. Дело в том, что бесконечная степенная башня не может быть последовательно неоднородной, то есть не сопоставима с последовательностью из убывающих по длине палочек из Рисунка №32. Как мы выяснили, тетрация строго последовательная операция и считается с конца, то есть каждый новый этаж степенной башни должен подставляться снизу, значит ^ω+1ℵ₀ должно быть равно ℵ₀^{(ℵ₀ℵ₀ℵ₀...)}, что при раскрытии скобок равно ℵ₀^{ℵ₀ℵ₀ℵ₀...} = ב_ω. И так будет происходить с любым трансфинтным ординалом подставленным в показатель тетрации, значит, используя тетрацию над кардиналами, мы так и не получим ничего бо́льшего ב_ω.

Кроме того стоит отметить, что кардинальность тоже определяется порядковыми числами ℵ₀ - нулевая бесконечная кардинальность, ℵ₁ - первая бесконечная кардинальность и так далее, но при этом можно продолжать использовать трансфинитные ординалы для выражения еще бо́льшей кардинальности: ℵ_ω, ℵ_ω+1, ℵ_ω×2, ℵ_ω², ℵ_ω1, ℵ_ω2, и т.д. Показать существование таких кардиналов как ℵ_ω, ℵ_ω×2 несложно, достаточно разложить их в ряд бесконечной суммы: ℵ_ω = ℵ₀+ℵ₁+ℵ₂+ℵ₃+... или ℵ_ω×2 = ℵ_ω+ℵ_ω+1+ℵ_ω+2+ℵ_ω+3+... Продолжая иерархию кардинальности алефов мы можем дойти до ℵ_ωωω..., которую называют лестницей бесконечности. Хотя иногда лестницу бесконечности записывают так ℵ_ℵℵℵ... и называют лестницей алефов. Но почему так делают, ведь мы то с вами знаем, что такая запись некорректная, потому что уровень кардинальности можно записывать только порядковым числом. Просто обычно, если на то место, где должен быть ординал, математики пишут кардинал, то подразумевают под ним наименьший ординал, кардинальность которого соотвествует этому кардиналу, например под ℵ_ℵ0 подразумевается ℵ_ω, а под ℵ_ℵ1 подразумевается ℵ_ω1.

Аналогично кардинальность Бет-кардиналов тоже может быть выражена только ординалами. Мы так же можем получить Бет-кардиналы с трансфитиным порядковым номером путем бесконечной суммы всех предыдущих Бет-кардиналов. И не забываем, что кардинальность Алеф-каридиналов (ℵ) и кардинальность Бет-кардиналов (ב) нельзя сопоставлять. Кроме того, так же иногда можно встретить, то что называют лестницей бетов ב_בבב... (это тоже не является корректной записью, потому что бет-кардиналы, тоже не являются ординалами), и то что под этим имеется ввиду не соотвествует ב_ωωω.... Давайте разберем почему. Допустим под ℵ_ℵ1 подразумавется ℵ_ω1, что оправдано, поскольку |ω₁| = ℵ₁. Однако ב_ב1 не может обозначать ב_ω1, потому что, если предположить, что континуум-гипотеза неверна, то |ω₁| < ב₁, а значит и наименьший ординал, кардинальность которого соответствует ב₁ будет намного больше ω₁.

Обычно наименьший ординал соответствующий ב₁ принято записывать так P(ω), а наименьший ординал соответствующий ב₂ так P(P(ω)), и т. д., с использованием оператора множества всех подмножеств. Делается это для того, чтобы различать их с ординалами соответствующими алефам, если мы используем их в аксиоматических системах, где континуум-гипотеза неверна, ведь в таких системах: ω₁ < P(ω), ω₂ < P(P(ω)), и т. д. Получается, что лестница бетов, если допустить ошибочность континуум-гипотезы, будет намного больше лестиницы алефов. Тем не менее, ни та, ни другая не является абсолютной бесконечностью, ведь иначе ее можно было бы назвать множеством всех множеств, а это, я напомню, страшный парадокс, разрушающий всю теорию множеств. На самом деле можно создать структуры еще бо́льшие, чем лестница алефов или лестница бетов, и мы с вами еще этим займемся. Понятно, что такие бесконечности и вовсе не имеют никакого отображения в любых разделах математики, и нужны только в теории множеств для изучения пределов ее возможностей, но нам они позже пригодятся для создания сверхбольших конечных чисел. Ну а все проявления количественной бесконечности, с которыми можно столкнуться в математике приведены ниже в Приложении №7.

Ну вот я и рассказал все начальные необходимые знания о бесконечности, которые помогут нам создавать очень сильные рекурсии, конечно в следующих главах я буду дополнять эти знания, но уже по мере необходимости. На этом столь грандиозное, но столь необходимое отступление от основной темы закончено и мы снова можем продолжать создавать сверхбольшие числа.

следующая часть...