Часть IV Рекурсии на несчетных рекурсиях
Суждение о множестве или его элементах может быть эквивалентно другому множеству, но само по себе никогда не является им - следствие Аксиом Выделения, Преобразования и Свертывания.
Приветствую всех кто добрался до четвертой части, и раз уж вы здесь, то вероятно вы серьезно настроены разобраться в теме больших чисел. Но перед тем как идти дальше нам опять необходимо определить подсистему арифметики второго порядка, в которой мы будем создавать рекурсии. И раз уж мы решительны в своем намерении постичь большие числа, то нам просто необходимо понять сами принципы выделения этих подсистем. Как всегда начнем издалека, и чтобы понять как создаются некоторые подсистемы арифметики разных порядков, давайте сперва поговорим о средствах языка, на котором формулируются аксиомы.
Средства формулировки аксиом и теорем на их основе изучаются математической логикой, а это отдельный раздел математики. Так давайте немного погрузимся в математическую логику и дадим определение понятию формула. Формула - это выражение, которое состоит из предикатов, функций и переменных. Под функцией подразумевают функцию определенную на числах или множествах, как минимум арифметическую. Например, операции " +, ×, - , / " однозначно являются функциями, причем 2-арными (бинарными), то есть принимающими два аргумента. Операции a! - факториал, |a| - модуль и т.п. называют 1-арными (унитарными), то есть принимающими один аргумент. Функции 0-арные, не принимающие аргументов, называют константами, например, если в выражении встретилось какое-либо число, допустим "2", это можно считать 0-арной функцией, результат которой всегда равен 2, вероятно это звучит излишне усложнено и запутано, зато позволяет встроить все в одну общую схему. В языке арифметики в качестве переменных a, b, c, x, y, z,... могут выступать числа, или A, B, C, X, Y, Z,... - множества, если мы говорим о языке арифметики второго порядка.
А вот о том, что такое предикаты - мы поговорим отдельно. Предикатом называют математическое суждение, или логическую функцию. Например, операции " < , ≤ , > , ≥ , = , ≠ " являются 2-арными (бинарными) предикатами, то есть выносящими математическое суждение о двух аргументах, результатом логического суждения может быть либо "правда" (true), либо "ложь" (false). Предикаты тоже могут принимать разное число аргументов, например, быть 1-арными (унитарными), как ¬a - логическое отрицание, или 0-арными, не принимающими аргументов - логическими константами, например, просто "true". Предикаты так же как и функции могут быть простыми (не составными) и сложными (составными). Последние это такие, которые включают в себя другие предикаты или функции.
Как всегда разобраться в теории без примеров многим будет сложно, поэтому привожу формулу, которую мы разберем на составляющие. Формула y!×(x+5) ≤ z состоит из 2-арного предиката "≤", который принимает два аргумента: y!×(x+5) и переменную "z"; аргумент y!×(x+5) является 2-арной функцией "×", которая состоит из аргументов (x+5) и y!, каждый из которых тоже является функцией: первая функция 1-арная "!" на переменной "y", а вторая 2-арная функция "+", принимающая два аргумента: переменную "x" и 0-арную функцию (константу), всегда равную "5".
А теперь я расскажу о кванторах, так называют специальные ограничители, которые задают область распространения предиката. Допустим я высказываю такое математическое суждение: "каждое четное число делится на два", формально я должен записать это суждение следующим образом: ∀x∈E∃y∈N(x/2=y), что дословно расшифровывается так: для любого x являющегося четным числом, существует y являющееся натуральным числом, так что при делении x на 2 получится y (где N - множество натуральных чисел, E - множество четных чисел). Знаки "∀" и "∃" как раз являются кванторами, которые определяют область действия предиката x/2=y. "∀" называют квантором всеобщности и расшифровывается он как "для каждого", "∀" называют квантором существования и расшифровывается он как "существует". Формально квантор всеобщности на неком предикате определяется так: ∀P(x) = "P(x1) и P(x2) и P(x3) и ...", ну а квантор существования так: ∃P(x) = "P(x1) или P(x2) или P(x3) или ...". Эти предикаты неизбежно возникают в определении достаточно сложных формул. Если в приложениях, в которых приводились аксиомы к разным теориям, вы пропустили формальное определение этих аксиом, то теперь вы можете к ним вернуться и, уже зная что такое предикаты и кванторы, попробовать расшифровать это формальное определение.
Вам будет проще понять идею квантификации, если вы хотя бы немного знакомы с программированием. В программировании кванторы можно выразить как циклы, то есть повторяющиеся операции с неким условием завершения этого цикла. Так например, квантор "∀" эквивалентен циклу while(P(x) = true), где P(x) некий предикат, то есть логическая функция над переменной x. Иными словами цикл работает пока x удовлетворяет некому условию. В свою очередь квантор "∃" эквивалентен циклу while(P(x) = false), где P(x) некий предикат, то есть логическая функция над переменной x. Это когда цикл работает до тех пор пока x не удовлетворит некому условию. Вроде бы оба примера похожи, и может показаться, что один можно легко превратить в другой. А вот и нет, такое превращение while(P(x) = true) ↔ while(P(x) = false) возможно далеко не всегда.
Теперь, когда вы знаете что такое квантификация, я расскажу вам об еще одной важной вещи, настолько важной, что если вы ее не поймете, то ближе к концу книги, когда мы будем обсуждать уже невероятно сильные рекурсии, вы совсем не сможете в них разобраться без этих знаний. Знакомьтесь: Арифметическая иерархия! В двух словах это классификация рекурсивных формул на основе принципов квантификации. Дело в том, что любую рекурсивную функцию мы можем записать как формулу содержащую простые функции объединенные кванторами в более сложные функции. Начну с объяснения самых простых рекурсий, которые создаются примитивно-рекурсивными функциями, можете посмотреть в третьей главе их полное определение, в двух словах напомню, что это функции выражаемые при помощи циклов, в которых заранее известно количество итераций (таких циклов, в которых мы можем быть уверены, что в них не возникнет бесконечная петля при вычислении и наш компьютер на зависнет). В программировании такие циклы будут выглядеть так: while(x<y) или while(x>y), причем любую примитивную рекурсию можно выразить как при помощи первого вида циклов, так и при помощи второго вида циклов, а это значит, что квантификации ∀x(x<y) и ∃x(x<y) полностью эквивалентны, такие квантификации и называют ограниченными. Формулы, которые содержат только ∀x(x<y), называют П0-формулами, а формулы, которые содержат только ∃x(x<y), называют Σ0-формулами. Как мы выяснили, в случае ограниченной квантификации не имеет значения какой квантор использовать "∀" или "∃", все равно П0-формулы будут эквивалентны Σ0-формулам.
Рекурсивные функции на языкe программирования C++
Функции сложения, умножения, степени, тетрации, ... или, в общем случае a[k]b для любого k - называются примитивно-рекурсивными - их можно разложить на более простые функции, каждая из которых в конечном счете содержит функции обнуления
(x = 0), функции проекции
(x = y), функции следования
(x++) и ограниченную квантификацию в виде циклов
while(x<y) или
while(x>y).
int add(int a,int b){
int i = 0;
while (i < b){
a++;
i++;
}
return a;
}
int mul(int a,int b){
int r = 0
int i = 0;
while (i < b){
r = add(a,r);
i++;
}
return r;
}
int pow(int a,int b){
int r = 1;
int i = 0;
while (i < b){
r = mul(a,r);
i++;
}
return r;
}
int tetra(int a,int b){
int r = 1;
int i = 0;
while (i < b){
r = pow(a,r);
i++;
}
return r;
}
Каждую из этих функций можно переписать с использованием цикла for (в котором заранее известно количество итераций).
int add(int a,int b){
for (int i=0; i<b; i++) a++;
return a;
}
int mul(int a,int b){
int r = 0;
for (int i=0; i<b; i++) r = add(a,r);
return r;
}
int pow(int a,int b){
int r = 1;
for (int i=0; i<b; i++) r = mul(a,r);
return r;
}
int tetra(int a,int b){
int r = 1;
for (int i=0; i<b; i++) r = pow(a,r);
return r;
}
Или можно представить в явно рекурсивном виде, когда функция ссылается сама на себя.
int add(int a,int b){
if (b > 0) return add(a+1,b-1);
else return a;
}
int mul(int a,int b){
if (b == 0) return 0;
else if (b > 0) return add(a,mul(a,b-1));
else return a;
}
int pow(int a,int b){
if (b == 0) return 1;
else if (b > 0) return mul(a,pow(a,b-1));
else return a;
}
int tetra(int a,int b){
if (b == 0) return 1;
else if (b > 0) return pow(a,tetra(a,b-1));
else return a;
}
Функция Аккермана является самой простой функцией, которая не является примитивно-рекурсивной, она может быть представлена в явно рекурсивном виде:
int ackermann(int m, int n){
if (m = 0) return n+1;
else if (n = 0) return ackermann(m-1, 1);
else return ackermann(m-1, ackermann(m, n-1));
}
Однако ее нельзя расписать в виде функции или последовательности вложенных функций с использованием циклов for (в котором заранее известно количество итераций), тем не менее остается возможность записать ее с использованием цикла while(true), который уже не будет являться ограниченно квантифицированным. Внутри цикла будет происходить процесс рекурсии аналогичный ограниченной квантификации
(Σ0 = П0), но остановка данного цикла не зависит от этой рекурсии, а определяется по методу исключений, значит такой цикл является неограниченной квантификацией уровня П
1.
int ackermann(int m, int n) {
int v[n];
int s = 0;
while (true) {
if (m == 0) {
n++;
if (s-- == 0) break;
m = v[s];
continue;
}
if (n == 0) {
m--;
n = 1;
continue;
}
int i = s++;
v[i] = m - 1;
n--;
}
return n;
}
приложение 17 (Рекурсивные функции на языке программирования C++)
Функции, которые не являются примитивно-рекурсивными, нельзя выразить при помощи ограниченной квантификации, то есть на основе П0-формул или Σ0-формул, для них может потребоваться квантификация некого произвольного предиката. Как я и говорил ранее для вычисления таких функций нам необходимы такие условия выхода из цикла, которые не зависят напрямую от происходящей в нем рекурсии. Конечно внутри цикла будет происходить вычисление на основе П0-формул или Σ0-формул, однако выход из верхнего цикла определяется по методу исключения, то есть при программировании такой формулы мы заранее не можем знать сколько раз сработает цикл, и чисто теоретически, если внутренние П0-формулы или Σ0-формулы будут заданы неверно, то выход из цикла так и не произойдет и наш компьютер зависнет. Таких циклов основанных на исключениях можно задавать сколько угодно. Но как мы знаем исключения бывают двух видов, первый: P(x) = true - когда цикл работает пока условие удовлетворяет какому-либо требованию, второй: P(x) = false - когда цикл работает до тех пор пока условие не удовлетворит какому-либо требованию. Интересно то, что сила создаваемой рекурсии будет определяться не количеством подобных циклов, а за счет чередованием их вида. Так например, формула основанная только на первом виде циклов с исключениями будет формально записываться так ∀a∀b∀c∀...(f(a,b,c,z)) [где f() - это П0-формула или Σ0-формула] - и будет называться П1-формулой, ну а формула основанная только на втором виде циклов с исключениями будет формально записываться так ∃a∃b∃c∃...(f(a,b,c,z)) [где f() - это П0-формула или Σ0-формула] - и будет называться Σ1-формулой. При этом каждая из формул ∃a∀b(f(a,b,z)) или ∀a∃b(f(a,b,z)) [где f() - это по-прежнему некая П0-формула или Σ0-формула] может быть сильнее любой из выше перечисленных Σ1-формул или П1-формул, и относится они будут уже к классу Σ2-формул и П2-формул соответственно. Теперь мы можем дать формальное определение понятию Пn-формула и Σn-формула:
Σn - ∃a1∃b1∃c1∃...∀a2∀b2∀c2∀...∃a3∃b3∃c3∃...∀a4∀b4∀c4∀...∃a5∃b5∃c5∃... ...QanQbnQcnQ...(f(a,b,c,z))
Пn - ∀a1∀b1∀c1∀...∃a2∃b2∃c2∃...∀a3∀b3∀c3∀...∃a4∃b4∃c4∃...∀a5∀b5∀c5∀... ...QanQbnQcnQ...(f(a,b,c,z))
где f() - некая П0-формула или Σ0-формула, Q будет квантором "∀" или "∃" в зависимости от четности n.
Тем, кому сложно понять такое формальное определение арифметической иерархии, я попробую объяснить все это еще раз, но уже немного упрощенно. П0-формула = Σ0-формула - это формула, которая содержит любое количество кванторов "∀" и "∃", но каждый из них ограничен тем, что может быть применим только к предикату (x<y). Поскольку П0-формулы и Σ0-формулы эквиваленты при вычислении, то следующие два определения для них тоже будут верными: (1) формула, которая содержит любое количество кванторов "∀", применимых только к предикату (x<y) и (2) формула, которая содержит любое количество кванторов "∃", применимых только к предикату (x<y). П1-формула - это формула, которая содержит любое количество кванторов "∀" (их можно применять к любым предикатам). Σ1-формула - это формула, которая содержит любое количество кванторов "∃" (их можно применять к любым предикатам). П2-формула - это формула, которая содержит любое количество кванторов "∀", за которым следует любое количество кванторов "∃". Σ2-формула - это формула, которая содержит любое количество кванторов "∃", за которым следует любое количество кванторов "∀". П3-формула - это формула, которая содержит любое количество кванторов "∀", за которым следует любое количество кванторов "∃", за которым следует любое количество кванторов "∀". Σ3-формула - это формула, которая содержит любое количество кванторов "∃", за которым следует любое количество кванторов "∀", за которым следует любое количество кванторов "∃". И так далее.
Как можно заметить из определения: П1-формулы включают в себя П0-формулы и Σ0-формулы, так же как Σ1-формулы включают в себя П0-формулы и Σ0-формулы. В свою очередь П2-формулы включают в себя П1-формулы и Σ1-формулы, так же как Σ2-формулы включают в себя П1-формулы и Σ1-формулы. И так далее. Поэтому подобную классификацию формул и называют арифметической иерархией. Однако пусть П0-формулы и Σ0-формулы эквивалентны, то есть могут быть выражены и так и так, но при этом всевозможные П1-формулы и Σ1-формулы уже нельзя выразить друг через друга, так же как Пn-формулы и Σn-формулы, где n>0; эквивалентно друг через друга можно выразить только часть из них. Как раз эту часть Пn-формул и Σn-формул, которую можно взаимовыразить, называют Δn-формулами. За исключением Σ0 = П0 = Δ0, потенциально возможные формулы Δn создают рекурсию слабее, чем Пn-формулы или Σn-формулы, но те в свою очередь, хоть и несводимы, создают одинаковые по силе рекурсии.
Теперь давайте поговорим об уровне переменных. Если в качестве переменных мы используем только натуральные числа, то это считается нулевым уровнем в арифметической иерархии и для разного вида формул записывается просто как "Σn", "Пn", "Δn" или же с применением верхнего индекса "Σ0n", "П0n", "Δ0n" (данная запись применяется редко). Если кроме натуральных чисел нам дозволено использовать в формулах еще и множества натуральных чисел, то это считается первым уровнем в арифметической иерархии и записывается так "Σ1n", "П1n", "Δ1n" (иногда это называют аналитической иерархией). Если мы так же можем пользоваться множествами множеств натуральных чисел, то это будет уже второй уровень и записываться будет так "Σ2n", "П2n", "Δ2n". И так далее, мы можем определять все бо́льшие и бо́льшие уровни арифметической иерархии. Общее правило взаимосвязи между уровнями будет следующее: Σmω = Пmω = Δmω = Σm+10 = Пm+10 = Δm+10. Нам же пока будет достаточно нулевого и первого уровня.
Вот теперь мы полностью готовы разбираться с правилами выделения подситем арифметики второго порядка. Еще раз напомню, что арифметика второго порядка это очень сильная арифметическая система, которая отличается от арифметики первого порядка тем, что мы можем использовать в ней не только натуральные числа, но и множества натуральных чисел. С точки зрения системы аксиом, она отличается тем, что в ней изменена аксиома индукции и добавлена аксиома свертывания. Напомню, что в своем стандартном виде аксиома индукции утверждает: то что в неком математическом суждении верно для некого натурального числа и верно для следующего за ним, должно быть верно для всех натуральных чисел (при этом "0" разрешено исключить из этого правила). В арифметике второго порядка в определении индукции понятие математического суждения заменено на понятие принадлежности к некому множеству, что позволяет включить в индукцию не только натуральные числа, но и множества натуральных чисел. Аксиома свертывания - это утверждение о том, что выделение подмножества на множестве натуральных чисел может быть сопоставлено некой формуле над этим подмножеством, что значит: каждой арифметической формуле может быть сопоставлено определенное подмножество натуральных чисел, которое будет ей эквивалентно (но тем не менее сама формула не является этим подмножеством). Эта аксиома и будет являться основным инструментом для выделения подсистем, нам всего лишь нужно ограничить уровень арифметической формулы, которая может быть сопоставлена с подмножеством натуральных чисел, методами арифметической иерархии.
Итак давайте разбирать на примерах: Σ0-СA0, П0-СA0, или Δ0-СA0 так будет называться подсистема арифметики второго порядка, в которой аксиома свертывания ограничена Σ0-формулами, П0-формулами, или Δ0-формулами, которые как мы знаем полностью эквивалентны друг другу. Но это еще не все, последний нолик в названии подсистемы говорит о том, что аксиома индукции тоже ограничена в рамках этих формул и распространяется только на них, если этого не сделать, то возможности подсистемы станут намного шире. Так вот, Σ0-СA0, П0-СA0, или Δ0-СA0 это все равнозначные определения RCA0 - Аксиом рекурсивного свертывания, что эквивалентно PRA - примитивно-рекурсивной арифметике, максимально возможная рекурсия и следовательно PTO этой подсистемы будут равны ωω. Интересно то, что Δ1-СA0 - подсистема арифметики второго порядка, в которой аксиома свертывания ограничена Δ1-формулами тоже будет иметь PTO равный ωω и будет эквивалентна RCA0 и PRA.
Подсистемы Σ1-СA0, П1-СA0 и Δ2-СA0 уже не будут полностью эквивалентны друг другу, потому что, как мы помним, формулы Пn и Σn, где n>0, нельзя взаимовыразить, однако максимально возможная рекурсия на основе этих аксиоматических систем будет одинаковой: PTO = ωωω. Соответственно PTO для подсистем Σ2-СA0, П2-СA0 и Δ3-СA0 будет равен ωωωω, и так далее. В арифметике первого порядка тоже можно выделить похожие подсистемы. Подсистемы арифметики первого порядка с ограниченной аксиомой индукции обычно кратко записывают так I'F', где на место 'F' подставляют тип формул из арифметической иерархии, на которые распространяется аксиома индукции, так IΣ0 = IП0 = IΔ0 = IΔ1 = PRA. Соответственно подсистемы IΣ1, IП1, IΔ2 будут сильнее, но уже не эквивалентны друг другу, однако все будут иметь PTO равный ωωω . Тогда у подсистем IΣ1, IП1, IΔ2 будет PTO равный ωωωω, и так далее. В общем случае мы даже можем вывести правило для определения PTO, которое будет работать для всех таких подсиcтем: PTO Σn-СA0 = PTO Пn-СA0 = PTO Δn+1-СA0 = PTO IΣn = PTO IПn = PTO IΔn+1 = n+2ω.
Теперь мы можем определить подсистемы Σω-СA0, Пω-СA0 и Δω-СA0, которые будут эквивалентны. Их следует понимать как арифметику второго порядка, в которой аксиома свертывания ограничена только для формул на натуральных числах с использованием любого числа кванторов, любых видов и в любом порядке (то есть речь идет о любых арифметических формулах на натуральных числах). Как мы помним, по-другому эту подсистему называют ACA0 (Аксиомами арифметического свертывания), которая эквивалентна Арифметике Пеано (PA) - обычной арифметике первого порядка (в которой вообще нет множеств), она же будет эквивалентна Σ10-СA0, П10-СA0 и Δ10-СA0, то есть арифметике второго порядка, в которой аксиома свертывания ограничена только для формул на множествах натуральных чисел с использованием кванторов, применимых только к предикату (x<y). Ну и наконец, Δ11-СA0 тоже будет эквивалентна ACA0, где под Δ11 - понимаются формулы на множествах натуральных чисел, с использованием любого количества кванторов "∀", такие что их можно выразить с использованием любого количества кванторов "∃", и наоборот. Так же если в подсистемах Σn-СA0, Пn-СA0 и Δn-СA0 мы не будем ограничивать аксиому индукции, а оставим ее в том виде, в котором она определена в полной системе арифметики второго порядка, то тогда подсистемы следует записывать так Σn-СA, Пn-СA, и Δn-СA - как я и говорил, они станут сильнее и тоже будут эквивалентны ACA0. Однако стоит отметить, что в ACA0 аксиома индукции тоже ограничена тем, что сформулирована так как она определена в арифметике первого порядка (во всех более сильных подсистемах под ограничением аксиомы индукции будет подразумеваться именно это), только с таким ограничением ACA0 эквивалентна PA и ее PTO = ε0. В случае, если мы оставим аксиому индукции не ограниченной, такой какой она определена в полной системе арифметики второго порядка, то тогда подсистема будет называться ACA и ее PTO станет равен εε0, а это значит, что в такой подсистеме есть возможность создать более сильные рекурсии.
Если с приставками Σmn, Пmn, Δmn и суффиксами CA и CA0 вам все уже должно быть понятно, то теперь нам с вами еще следует разобрать такие суффиксы: TR0, ТR, CA+BI. Все они тоже обозначают изменения в аксиоме индукции. TR0 - значит, что индукция сформулирована для арифметических формул как в арифметике первого порядка, но допускает свое применение не только к натуральным числам, но и к трансфинитным ординалам. TR - значит, что индукция сформулирована как в полной системе арифметики второго порядка, то есть в определении вместо "суждения над натуральными числами" используется "принадлежность натуральных чисел к множеству", ну и само понятие натуральных чисел так же может быть расширено до трансфинитных ординалов. Наконец, CA+BI - означает применение аксиомы ограничивающей индукции, которая взамен классической формулировки предлагает другую: "что верно для бесконечной последовательности натуральных чисел, будет верно и для любого ее конечного участка". Каждая подобная модификация аксиомы индукции создает разные по силе аксиоматические системы.
На самом деле есть еще огромное количество других способов изменить аксиомы арифметики второго порядка, сделав их слабее, и выделяя тем самым другие подсистемы аксиом, но в рамках данной книги нам достаточно и этих способов. Поэтому теперь, вооружившись всеми нашими знаниями, давайте сопоставим все подсистемы арифметики второго порядка, какие мы сможем выделить, в порядке возрастания их силы и начнем с тех, рекурсивные возможности которых мы уже преодолели в нашей погоне за большими числами.
| Подсистема |
Изменение аксиом |
PTO |
Σ0-CA0
П0-CA0
Δ0-CA0
Δ1-CA0
[RCA0]
[PRA] |
Акс. свертывания ограничена Σ0-формулами, Акс. индукции ограничена Σ0-формулами
Акс. свертывания ограничена П0-формулами, Акс. индукции ограничена П0-формулами
Акс. свертывания ограничена Δ0-формулами, Акс. индукции ограничена Δ0-формулами
Акс. свертывания ограничена Δ1-формулами, Акс. индукции ограничена Δ1-формулами
общее название: "Аксиомы рекурсивного свертывания"
эквивалентно "Примитивно рекурсивной арифметике первого порядка" |
ωω |
Σ1-CA0
П1-CA0
Δ2-CA0 |
Акс. свертывания ограничена Σ1-формулами, Акс. индукции ограничена Σ1-формулами
Акс. свертывания ограничена П1-формулами, Акс. индукции ограничена П1-формулами
Акс. свертывания ограничена Δ2-формулами, Акс. индукции ограничена Δ2-формулами |
ωωω |
Σ2-CA0
П2-CA0
Δ3-CA0 |
Акс. свертывания ограничена Σ2-формулами, Акс. индукции ограничена Σ2-формулами
Акс. свертывания ограничена П2-формулами, Акс. индукции ограничена П2-формулами
Акс. свертывания ограничена Δ3-формулами, Акс. индукции ограничена Δ3-формулами |
ωωωω |
Σ3-CA0
П3-CA0
Δ4-CA0 |
Акс. свертывания ограничена Σ3-формулами, Акс. индукции ограничена Σ3-формулами
Акс. свертывания ограничена П3-формулами, Акс. индукции ограничена П3-формулами
Акс. свертывания ограничена Δ4-формулами, Акс. индукции ограничена Δ4-формулами |
ωωωωω |
Σn-СA
Пn-СA
Δn-СA
[RCA]
Σω-СA0
Пω-СA0
Δω-СA0
Σ10-CA0
П10-CA0
Δ10-CA0
Δ11-CA0
[ACA0]
[PA] |
Акс. свертывания ограничена Σn-формулами, Акс. индукции 2-го порядка
Акс. свертывания ограничена Пn-формулами, Акс. индукции 2-го порядка
Акс. свертывания ограничена Δn-формулами, Акс. индукции 2-го порядка
общее название: "Аксиомы рекурсивного свертывания без ограничения индукции"
Акс. свертывания ограничена Σω-формулами, Акс. индукции ограничена Σω-формулами
Акс. свертывания ограничена Пω-формулами, Акс. индукции ограничена Пω-формулами
Акс. свертывания ограничена Δω-формулами, Акс. индукции ограничена Δω-формулами
Акс. свертывания ограничена Σ10-формулами, Акс. индукции 1-го порядка
Акс. свертывания ограничена П10-формулами, Акс. индукции 1-го порядка
Акс. свертывания ограничена Δ10-формулами, Акс. индукции 1-го порядка
Акс. свертывания ограничена Δ11-формулами, Акс. индукции 1-го порядка
общее название: "Аксиомы арифметического свертывания"
эквивалентно "Арифметике первого порядка (Аксиомам Пеано)" |
ε0 |
Σ10-CA
П10-CA
Δ10-CA
[ACA] |
Акс. свертывания ограничена Σ10-формулами, Акс. индукции 2-го порядка
Акс. свертывания ограничена П10-формулами, Акс. индукции 2-го порядка
Акс. свертывания ограничена Δ10-формулами, Акс. индукции 2-го порядка
общее название: "Аксиомы арифметического свертывания без ограничения индукции" |
εε0 |
| Δ11-CA |
Акс. свертывания ограничена Δ11-формулами, Акс. индукции 2-го порядка |
φ(ε0,0) |
П10-TR0
Σ10-TR0
[ATR0] |
Акс. свертывания ограничена Σ10-формулами, Акс. трансфинитной индукции 1-го порядка
Акс. свертывания ограничена П10-формулами, Акс. трансфинитной индукции 1-го порядка
общее название: "Арифметическая трансфинитная рекурсия" |
φ(1,0,0) |
П10-TR
Σ10-TR
[ATR] |
Акс. свертывания ограничена Σ10-формулами, Акс. трансфинитной индукции 2-го порядка
Акс. свертывания ограничена П10-формулами, Акс. трансфинитной индукции 2-го порядка
общее название: "Арифметическая трансфинитная рекурсия без ограничения индукции" |
φ(1,0,ε0) |
| Δ11-TR0 |
Акс. свертывания ограничена Δ11-формулами, Акс. трансфинитной индукции 1-го порядка |
φ(1,ω,0) |
| Δ11-TR |
Акс. свертывания ограничена Δ11-формулами, Акс. трансфинитной индукции 2-го порядка |
φ(1,ε0,0) |
П10-CA+BI
Σ10-CA+BI
Δ11-CA+BI
[ACA+BI] |
Акс. свертывания ограничена Σ10-формулами, Акс. ограничивающей индукции
Акс. свертывания ограничена П10-формулами, Акс. ограничивающей индукции
Акс. свертывания ограничена Δ11-формулами, Акс. ограничивающей индукции
общее название: "Аксиомы арифметического свертывания с ограничивающей индукцией" |
ψ(ωΩ) |
таб.20
А в следующей таблице так же в порядке возрастания их рекурсивной силы приведем подсистемы арифметики второго порядка, пределы возможностей которых нам только предстоит достичь. В ней же я приведу PTO этих подсистем, и пусть вам пока они будут не понятны, но вы всегда можете вернуться к этой таблице по мере того как постигнете масштабы этих ординалов.
| Подсистема |
Изменение аксиом |
Σ11-CA0
П11-CA0
Δ12-CA0 |
Акс. свертывания ограничена Σ11-формулами, Акс. индукции 1-го порядка
Акс. свертывания ограничена П11-формулами, Акс. индукции 1-го порядка
Акс. свертывания ограничена Δ12-формулами, Акс. индукции 1-го порядка
PTO = ψ(Ωω) |
Σ11-CA
П11-CA |
Акс. свертывания ограничена Σ11-формулами, Акс. индукции 2-го порядка
Акс. свертывания ограничена П11-формулами, Акс. индукции 2-го порядка
PTO = ψ(Ωω×ε0) |
Σ11-CA+BI
П11-CA+BI |
Акс. свертывания ограничена Σ11-формулами, Акс. ограничивающей индукции
Акс. свертывания ограничена П11-формулами, Акс. ограничивающей индукции
PTO = ψ(εΩω+1) |
| Δ12-CA |
Акс. свертывания ограничена Δ12-формулами, Акс. индукции 2-го порядка
PTO = ψ(Ωε0) |
Σ11-TR0
П11-TR0 |
Акс. свертывания ограничена Σ11-формулами, Акс. трансфинитной индукции 1-го порядка
Акс. свертывания ограничена П11-формулами, Акс. трансфинитной индукции 1-го порядка
PTO = ψ(ψI(0)) |
Σ11-TR
П11-TR |
Акс. свертывания ограничена Σ11-формулами, Акс. трансфинитной индукции 2-го порядка
Акс. свертывания ограничена П11-формулами, Акс. трансфинитной индукции 2-го порядка
PTO = ψ(ψI(0)×ε0) |
| Δ12-TR0 |
Акс. свертывания ограничена Δ12-формулами, Акс. трансфинитной индукции 1-го порядка
PTO = ψ(Iω) |
| Δ12-TR |
Акс. свертывания ограничена Δ12-формулами, Акс. трансфинитной индукции 2-го порядка
PTO = ψ(Iε0) |
| Δ12-CA+BI |
Акс. свертывания ограничена Δ12-формулами, Акс. ограничивающей индукции
PTO = ψ(εI+1) |
Σ12-CA0
П12-CA0
Δ13-CA0 |
Акс. свертывания ограничена Σ12-формулами, Акс. индукции 1-го порядка
Акс. свертывания ограничена П12-формулами, Акс. индукции 1-го порядка
Акс. свертывания ограничена Δ13-формулами, Акс. индукции 1-го порядка
PTO = PTO KP+S[σω] ?! |
Σ12-CA
П12-CA |
Акс. свертывания ограничена Σ12-формулами, Акс. индукции 2-го порядка
Акс. свертывания ограничена П12-формулами, Акс. индукции 2-го порядка
PTO = PTO KP+S[Sω[σω]×ε0] ?! |
Σ12-CA+BI
П12-CA+BI |
Акс. свертывания ограничена Σ12-формулами, Акс. ограничивающей индукции
Акс. свертывания ограничена П12-формулами, Акс. ограничивающей индукции
PTO = PTO KP+S[σω+1] ?! |
| Δ13-CA |
Акс. свертывания ограничена Δ13-формулами, Акс. индукции 2-го порядка
PTO = PTO KP+S[σε0] ?! |
Σ12-TR0
П12-TR0 |
Акс. свертывания ограничена Σ12-формулами, Акс. трансфинитной индукции 1-го порядка
Акс. свертывания ограничена П12-формулами, Акс. трансфинитной индукции 1-го порядка
PTO = PTO KP+S[SS[σσ](1|σσ|0)] ?! |
Σ12-TR
П12-TR |
Акс. свертывания ограничена Σ12-формулами, Акс. трансфинитной индукции 2-го порядка
Акс. свертывания ограничена П12-формулами, Акс. трансфинитной индукции 2-го порядка
PTO = PTO KP+S[SSS[σσ](1|σσ|0)[SS[σσ](1|σσ|0)]×ε0] ?! |
| Δ13-TR0 |
Акс. свертывания ограничена Δ13-формулами, Акс. трансфинитной индукции 1-го порядка
PTO = PTO KP+S[SS[σσ](ω|σσ|0)] ?! |
| Δ13-TR |
Акс. свертывания ограничена Δ13-формулами, Акс. трансфинитной индукции 2-го порядка
PTO = PTO KP+S[SS[σσ](ε0|σσ|0)] ?! |
| Δ13-CA+BI |
Акс. свертывания ограничена Δ13-формулами, Акс. ограничивающей индукции
PTO = PTO KP+S[SS[σσ'1]] ?! |
Σ13-CA0
П13-CA0
Δ14-CA0 |
Акс. свертывания ограничена Σ13-формулами, Акс. индукции 1-го порядка
Акс. свертывания ограничена П13-формулами, Акс. индукции 1-го порядка
Акс. свертывания ограничена Δ14-формулами, Акс. индукции 1-го порядка
PTO = PTO KP+S[SSω[σσω]] ?! |
Σ13-TR0
П13-TR0 |
Акс. свертывания ограничена Σ13-формулами, Акс. трансфинитной индукции 1-го порядка
Акс. свертывания ограничена П13-формулами, Акс. трансфинитной индукции 1-го порядка
PTO = PTO KP+S[SS[SSS[σσσ](1|σσσ|0)]]] ?! |
Σ14-CA0
П14-CA0
Δ15-CA0 |
Акс. свертывания ограничена Σ14-формулами, Акс. индукции 1-го порядка
Акс. свертывания ограничена П14-формулами, Акс. индукции 1-го порядка
Акс. свертывания ограничена Δ15-формулами, Акс. индукции 1-го порядка
PTO = PTO KP+S[SS[SSSω[σσσω]]] ?! |
Σ14-TR0
П14-TR0 |
Акс. свертывания ограничена Σ14-формулами, Акс. трансфинитной индукции 1-го порядка
Акс. свертывания ограничена П14-формулами, Акс. трансфинитной индукции 1-го порядка
PTO = PTO KP+S[SS[SSS[SSSS[σσσσ](1|σσσσ|0)]]]] ?! |
Σ1ω-CA
П1ω-CA
Δ1ω-CA
[Z2] |
Акс. свертывания 2-го порядка для любых Σ1ω-формул. Акс. индукции 2-го порядка
Акс. свертывания 2-го порядка для любых П1ω-формул. Акс. индукции 2-го порядка
Акс. свертывания 2-го порядка для любых Δ1ω-формул. Акс. индукции 2-го порядка
общее название: "Полные аксиомы арифметики второго порядка"
PTO = PTO KP+S[S(ω)[σ(ω)]] ?! |
таб.21
Хочу сразу предупредить вас, что на сегодняшний день предел рекурсивных возможностей арифметики второго порядка до сих пор не достигнут, есть исследовательские работы или гипотетические разработки на счет этого, но не существует гарантированной рабочей ординальной нотации, такой в которой можно было бы показать, что она является вполне упорядоченной, так чтобы можно было проверить все ее фундаментальные последовательности. Самое большое что профессионально изучалось со всеми доказательствами - это рекурсивный предел подсистемы П12-CA0 (однако, как оказалось, эта работа содержала ряд технических ошибок, так что фактически фундаментальные последовательности этого предела тоже не рабочие). Для более сильных систем PTO, которые я привел в таблице, не имеют надежной проверенной ординальной нотации, способной расписать их фундаментальные последовательности, а саму запись таких PTO следует считать условной (поэтому я отметил их знаком "?!"). Мы с вами тоже доберемся до этих зыбких полугипотетических масштабов, но пока что мы стоим на твердой почве Ординальной коллапсирующей функции Бухольца, по которой легко сможем добраться до пределов П11-CA0. На этом я заканчиваю данное отступление и мы с вами снова продолжаем карабкаться вверх.
В конце третьей части мы остановились на ψ(ωΩ), который именовался Ординалом Бахмана-Говарда, в сущности он представляет собой бесконечную степенную башню их несчетных ординалов внутри коллапсирующей функции. Как мы с вами выяснили арифметические действия выше уровня ωn над ординалами уже не применимы, при чем не важно над счетными или над несчетными, однако мы можем воспользоваться особенностями ординальной арифметики чтобы продолжить рекурсии дальше. Помните в третьей части мы вывели с вами два важных принципа: первый - ωα+1 = α×ω, если ωα = α; и второй: εα+1 = ωα, если ωα = α; так вот эту особенность ординальной арифметики можно применить и к несчетным ординалам:
Ω×ω = ωΩ+1
Ω2 = ωΩ×2
Ωω = ωωΩ+1
ΩΩ = ωωΩ×2
ΩΩω = ωωωΩ+1
ΩΩΩ = ωωωΩ×2
ΩΩΩω = ωωωωΩ+1
ΩΩΩΩ = ωωωωΩ×2
ΩΩΩΩω = ωωωωωΩ+1
εΩ+1 = ΩΩΩΩ...= ωωω...Ω+1
Выражение арифметики любых больших ординалов до уровня ω-тетрации таким способом, называется применением нормальной формы Кантора (Cantor normal form - CNF), с ней мы уже встречались, когда обсуждали нотацию Кантора, так вот с ее помощью можно увеличить любой ординал α, такой что ωα = α, до уровня εα+1. Обращаю ваше внимание, что такое выражение εΩ будет равно просто Ω, так же как εζ0 = ζ0, εη0 = η0, и т.д. Так проиходит потому что εΩ обозначает неподвижную точку α↦ωα (ωωωω...) под номером Ω - несчетного ординала, которая и будет, по сути, несчетным ординалом, однако εΩ+1 будет означать следующую неподвижную точку α↦ωα (ωωωω...), идущую после Ω и, собственно, равную ωωω...Ω+1 или ΩΩΩΩ... = ωΩ. Таким образом, мы можем продолжать наращивать рекурсии на Ω и после ωΩ. Например, выражение εΩ+2 будет означать вторую неподвижную точку α↦ωα (ωωωω...), идущую после Ω, и будет равно εΩ+1εΩ+1εΩ+1εΩ+1... = ωωω...εΩ+1. Так же как мы делали ранее, когда очень условно сопоставляли высшие арифметические действия с расширенной ординальной нотацией Кантора, так же очень условно мы можем сопоставить εΩ+2 ≅ ω×2Ω. Соотвественно, εΩ+3 = εΩ+2εΩ+2εΩ+2εΩ+2... = ωωω...εΩ+2 ≅ ω×3Ω. Продолжая создавать подобные неподвижные точки, сразу перейдем к их трансфинитным значениям: εΩ+ω = εΩ+ψ(1), εΩ+ε0 = εΩ+ψ(Ω), εΩ+Г0 = εΩ+ψ(2Ω), ..., εΩ+ψ(ωΩ) = εΩ+ψ(εΩ+1). Так можно добраться до εΩ+Ω, которую в рамках коллапсирующей функции можно представить как диагонализацию: ψ(εΩ+Ω) = ψ(εΩ×2) = ψ(εΩ+ψ(εΩ+ψ(εΩ+...))). Ну а затем, как мы уже умеем, создадим последовательность диагонализаций используя Ω - несчетный ординал: ψ(εΩ×Ω) = ψ(εΩ2) = ψ(εΩ×ψ(εΩ×ψ(εΩ×...))), ψ(εΩΩ)= ψ(εΩψ(εΩψ(εΩ...))), и т.д., до тех пор пока ψ(εεΩ+1) = ψ(εΩΩΩΩ...), ну а затем ψ(εεεΩ+1) = ψ(εεΩΩΩΩ...), и так до ψ(εεε...Ω+1), что уже следует считать следующей неподвижной точкой α↦εα (εεεε...), идущей после Ω, которую можно записать так ζΩ+1. Опять же очень условно ее можно сравнить с пентацией ζΩ+1 ≅ Ω[5]ω, так же как мы делали это ранее для ζ0 ≅ ω[5]ω. Чтобы не ходить вокруг да около, сразу перейдем к ζζζ...Ω+1 = ηΩ+1 следующей неподвижной точке α↦ζα (ζζζζ...), идущей после Ω, так же условно сопоставимой с гексацией ηΩ+1 ≅ Ω[6]ω. Такие условные сопоставления возможны только до уровня ГΩ+1, что вероятно было бы эквивалентно ГΩ+1 ≅ ...[Ω[Ω[Ω]Ω]Ω]..., но поэтапно добраться до этого уровня будет непросто.
Давайте позовем на помощь Функцию Веблена. Нам ничто не мешает, немного изменив ее опредение, применять ее на несчетных ординалах. Тогда εΩ+1 = φ(1,Ω+1), ζΩ+1 = φ(2,Ω+1), ηΩ+1 = φ(3,Ω+1), и так до φ(ω,Ω+1). Как мы помним, φ(ω,1) был пределом последовательности {ωφ(ω,1)+1 = φ(φ(ω,1)+1), εφ(ω,1)+1 = φ(1,φ(ω,1)+1), ζφ(ω,1)+1 = φ(2,φ(ω,1)+1), ηφ(ω,1)+1 = φ(3,φ(ω,1)+1), ... }, соответственно φ(ω,Ω+2) будет пределом последовательности {ωφ(ω,Ω+1)+1 = φ(φ(ω,Ω+1)+1), εφ(ω,Ω+1)+1 = φ(1,φ(ω,Ω+1)+1), ζφ(ω,Ω+1)+1 = φ(2,φ(ω,Ω+1)+1), ηφ(ω,Ω+1)+1 = φ(3,φ(ω,Ω+1)+1), ... }. Дальше тоже все аналогично, как φ(ω+1,0) являлась первой неподвижной точкой α↦φ(ω,α), для последовательности {φ(ω,1), φ(ω,φ(ω,1)), φ(ω,φ(ω,φ(ω,1))), ...}, так же и φ(ω+1,Ω+1) является первой неподвижной точкой для последовательности {φ(ω,Ω+1), φ(ω,φ(ω,Ω+1)), φ(ω,φ(ω,φ(ω,Ω+1))), ...}. В общем, используя аналогии тех рекурсий, что мы создавали на счетных ординалах, делаем тоже самое с нечетными. Например, запишем такое выражение: φ(φ(φ(φ(...,0),0),0),Ω+1) = φ(Г0,Ω+1) = φ(ψ(ΩΩ),Ω+1). Дальше φ(ψ(εΩ+1),Ω+1) = φ(ψ(φ(1,Ω+1)),Ω+1), потом φ(ψ(φ(ψ(1,Ω+1)),Ω+1)),Ω+1) и так, в рамках ординальной коллапсирующей функции, мы можем дойти до α↦ψ(φ(α,Ω+1)) = ψ(φ(ψ(φ(ψ(φ(ψ(φ(...,Ω+1)),Ω+1)),Ω+1)),Ω+1)), которую сможем диагонализировать таким образом ψ(φ(Ω,1)). Следующая диагонализация будет выглядеть так ψ(φ(Ω,Ω)) = ψ(φ(Ω,ψ(φ(Ω,ψ(φ(Ω,...)))))) = α↦ψ(φ(Ω,α)). Тогда, продолжая диагонализации дальше, получим: ψ(φ(Ω+1,0)) = ψ(φ(Ω,φ(Ω,φ(Ω,φ(Ω,...))))) = ψ(α↦φ(Ω,α)). Ну и, в конце концов, создавая череду выражений: ψ(φ(φ(Ω,1),0)), ψ(φ(φ(φ(Ω,1),0),0)), ψ(φ(φ(φ(φ(Ω,1),0),0),0)), ... мы наконец-то достигнем заветного ψ(φ(φ(φ(...φ(Ω,1)...,0),0),0)) = ψ(φ(1,0,Ω+1)) = ψ(ГΩ+1).
Дальше я не буду расписывать как можно продолжать накручивать рекурсии Функцией Веблена на Иерархии Бахмана. Пройдемся только по основным моментам. От выражения ψ(φ(1,0,Ω+1)) сразу перейдем к ψ(φ(1,0,0,...,Ω+1)), которое в матричном виде можно записать так ψ(φ(1ωΩ+10)). Отсюда сразу, минуя все промежуточные матричные представления Шутте, переходим к ψ(φ(1φ(1φ(1φ(1...))) Ω+10)) = ψ(φ(1ψ(ΩΩΩ) Ω+10)). Потом совершаем резкий скачек к ψ(φ(1ψ(φ(1ψ(ΩΩΩ) Ω+10)) Ω+10)). В итоге, если мы продолжим такую цепочку подстановок, наш ожидает неподвижная точка α↦ψ(φ(1α Ω+10)), которую мы можем диагонализировать так ψ(φ(1Ω10)). Это позволит довести Иерархию Веблена до своего апофеоза в виде последовательности: {ψ(φ(1Ω10)), ψ(φ(1φ(1Ω10))), ψ(φ(1φ(1φ(1Ω10)))), ..., ψ(φ(1φ(1φ(1...φ(1Ω10)...))))}. Но, так или иначе, это очень слабый способ усиления Иерархии Бахмана, поскольку для ее продолжения мы используем более слабую по сравнению с ней Иерархию Веблена. Чтобы по-настоящему усилить Иерархию Бахмана, нам нужна уже другая Иерархая Бахмана над ней.
Кроме того все рекурсии выше уровня εΩ+1 внутри коллапсирующей функции становятся условными, потому что в ее определении нет ни Расширенной нотации Кантора, ни Функции Веблена, поэтому без добавления их внутрь определения мы не сможем определить фундаментальные последовательности для функций быстрорастущих иерархий, которые нужны нам для вычисления конечного числа. Конечно их можно туда внедрить, но это только усложнит определение коллапсирующей функции, так же как и усложнит определение фундаментальных последовательностей, да к тому же, как мы выяснили, будет не эффективно с точки зрения усиления рекурсии, ведь, как мы помним, для настоящего усиления рекурсии требуется создать над ней другую рекурсию либо такую же по силе, либо еще сильнее. Как минимум такой же по силе будет рекурсия основанная на другой коллапсирующей функции.
Основная идея заключается в том же преемственном процессе рекурсирования. Как когда для создания рекурсий над конечными числами мы использовали счетные ординалы с кардианльностью ℵ0, и как когда для создания рекурсий над счетными ординалами мы использовали несчетные ординалы с кардианльностью ℵ1, так же для создания рекурсий над последними нам нужны ординалы с кардинальностью ℵ2. Наименьший ординал обладающий кардинальностью ℵ2 называется ω2 - это ординал идущий сразу после всех ординалов с кардинальностью ℵ1, то есть он точно больше чем любая рекурсия построенная на ординале ω1. Внутри коллапсирующей функции ординал ω2 принято записывать так Ω2. Ну а мы, получается, имеем уже две коллапсирующие функции, давайте их пронумеруем: ψ0(n) - это наша старая знакомая, с помощью которой создавались счетные ординалы из несчетных ординалов с кардианльностью ℵ1, тогда ψ1(n) - это будет новая коллапсирующая функция, с помощью которой будут создаваться несчетные ординалы с кардианльностью ℵ1, из несчетных ординалов с кардианльностью ℵ2. Работать она будет аналогично ψ0(n), только у нее будет расширена область определения и возвращать она всегда будет только несчетные ординалы с кардианльностью ℵ1. Кроме собственно ординалов с кардианльностью ℵ2 в нее так же можно подставлять меньшие по значению аргументы, в том числе конечные числа, счетные ординалы и несчетные ординалы с кардианльностью ℵ1. Так например, ψ1(0) = Ω, ψ1(1) = Ω×ω = ωΩ+1, ψ1(2) = Ω×ω2 = ωΩ+2, и т.д. В общем случае мы можем вывести правило: ψ1(n) = ωΩ+n. Тогда получается, что ψ1(Ω) = ψ1(ψ1(0)) = ωΩ+Ω = ωΩ×2 = Ω2, затем ψ1(Ω×2) = ψ1(ψ1(0)+ψ1(0)) = ωΩ+Ω+Ω = ωΩ×3 = Ω3. В итоге ψ1(Ω×Ω) = ψ1(Ω2) = ψ1(ψ1(ψ1(0))) = ωωΩ×2= ΩΩ. Череду подстановок можно продолжить и дальше ψ1(ψ1(ψ1(ψ1(0)))) = ωωωΩ×2 = ΩΩΩ , ψ1(ψ1(ψ1(ψ1(ψ1(0))))) = ωωωωΩ×2 = ΩΩΩΩ, пока не доберемся до ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(...))))))) = εΩ+1, Что и потребует от нас диагонализации соответствующего уровня ψ1(Ω2) = εΩ+1, так же как это было ранее для получения счетных ординалов ψ0(Ω) = ε0. Тогда полная запись Ординала Бахмана-Говарда должна выглядеть так: ψ0(ψ1(Ω2)), однако для краткости и в соотвествии с требованиями функции, как только у нас появляется диагонализатор верхнего уровня, цепь коллапсирующих функций не записывается и правильной будет запись просто ψ(Ω2).
Дальше все рекурсии идут по общим правилам коллапсирующей функции, и неважно что внутри нее уже есть ординал с кардианльностью ℵ2, поскольку это ординал его так же можно увеличивать по правилам ординальной арифметики обычными арифметическими действиями, каждое из которых на выходе из коллапсирующей функции создает рекурсии: ψ(Ω2)+ψ(Ω2)+ψ(Ω2)+... = ψ(Ω2+1) = ψ(εΩ+1)+ψ(εΩ+1)+ψ(εΩ+1)+... = ψ(εΩ+1)×ω = ωψ(εΩ+1)+1, ψ(Ω2+1)+ψ(Ω2+1)+ψ(Ω2+1)+... = ψ(Ω2+2) = ψ(εΩ+1)×ω×ω = ωψ(εΩ+1)+2 , ну и, следуя логике функции, получается, что ψ(Ω2+Ω) = ψ(εΩ+1)ψ(εΩ+1)ψ(εΩ+1)... = ψ(εΩ+1+Ω), затем ψ(Ω2+ΩΩΩΩ...) = ψ(Ω2+ψ1(Ω2)) = ψ(εΩ+1×2), потом ψ(Ω2+ψ1(Ω2+ψ1(Ω2))) = ψ(εΩ+12) = ψ(ωεΩ+1×2), сразу следом ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2)))) = ψ(εΩ+1εΩ+1) = ψ(ωωεΩ+1×2) и так мы постепенно доберемся до первой арифметической диагонализации на Ω2, которая будет равна ψ(Ω2+Ω2) = ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+...)))) = ψ(εΩ+1εΩ+1εΩ+1...) = ψ(ωωω...εΩ+1) = ψ(εΩ+2). Следующая диагонализация будет такой: ψ(Ω2×Ω2) = ψ(Ω2×ψ1(Ω2×ψ1(Ω2×ψ1(Ω2×...)))) = ψ(εεε...Ω+1) = ψ(ζΩ+1). Ну и соотвественно ψ(Ω2Ω2) = ψ(Ω2ψ1(Ω2ψ1(Ω2ψ1(...)))) = ψ(ГΩ+1), и уже ψ(Ω2Ω2Ω2) = ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2...)))) = ψ(φ(1φ(1φ(1...φ(1Ω10)...)))) станет пределом для Вебленских расширений рекурсий над Ω, так же как ψ0(ΩΩΩ) = φ(1φ(1φ(1φ(1...)))) стала пределом для Функции Веблена над счетными ординалами.
Чтобы еще раз хорошенько прочувствовать почему коллапсирование над коллапсированием будет правильным выбором в нашем дальнейшем пути, я привожу еще одну гигантскую сравнительную таблицу, где буду сравнивать возможности ψ0(n) и ψ0(ψ1(n)). В этой таблице можно еще раз наглядно проследить все пройденные нами рекурсии, но также она еще раз даст вам возможность убедиться в преимуществах иерархии Бахмана.
| ψ(Ω) |
ψ0(ψ1(0)) |
| ψ(Ω)+1 |
ψ0(ψ1(0))+ψ0(0) |
| ψ(Ω)+2 |
ψ0(ψ1(0))+ψ0(0)+ψ0(0) |
| ψ(Ω)+3 |
ψ0(ψ1(0))+ψ0(0)+ψ0(0)+ψ0(0) |
| ψ(Ω)+ψ(1) = ψ(Ω)+ω |
ψ0(ψ1(0))+ψ0(1) |
| ψ(Ω)+ω2 |
ψ0(ψ1(0))+ψ0(2) |
| ψ(Ω)+ωω |
ψ0(ψ1(0))+ψ0(ψ0(1)) |
| ψ(Ω)+ωωω |
ψ0(ψ1(0))+ψ0(ψ0(ψ0(1))) |
| ψ(Ω)+ωωω... = ψ(Ω)+ψ(Ω) |
ψ0(ψ1(0))+ψ0(ψ1(0)) |
| ψ(Ω)+ψ(Ω)+ψ(Ω) |
ψ0(ψ1(0))+ψ0(ψ1(0))+ψ0(ψ1(0)) |
| ψ(Ω+1) = ψ(Ω)×ω |
ψ0(ψ1(0)+ψ0(0)) |
| ψ(Ω+2) |
ψ0(ψ1(0)+ψ0(0)+ψ0(0)) |
| ψ(Ω+ψ(1)) = ψ(Ω+ω) |
ψ0(ψ1(0)+ψ0(1)) |
| ψ(Ω+ψ(Ω)) |
ψ0(ψ1(0)+ψ0(ψ1(0))) |
| ψ(Ω+ψ(Ω)+ψ(Ω)) |
ψ0(ψ1(0)+ψ0(ψ1(0))+ψ0(ψ1(0))) |
| ψ(Ω+ψ(Ω+1)) |
ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(0))) |
| ψ(Ω+ψ(Ω+ψ(Ω))) |
ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(ψ1(0)))) |
| ψ(Ω+ψ(Ω+ψ(Ω+1))) |
ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(0)))) |
| ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)))) |
ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(ψ1(0))))) |
| ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1)))) |
ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(0))))) |
| ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω))))) |
ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(ψ1(0)))))) |
| ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1))))) |
ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(0)))))) |
| ψ(Ω×2) = ψ(Ω+Ω) |
ψ0(ψ1(0)+ψ1(0)) |
| ψ(Ω×3) = ψ(Ω×2+Ω) |
ψ0(ψ1(0)+ψ1(0)+ψ1(0)) |
| ψ(Ω×4) = ψ(Ω×3+Ω) |
ψ0(ψ1(0)+ψ1(0)+ψ1(0)+ψ1(0)) |
| ψ(Ω×ω) |
ψ0(ψ1(1)) |
| ψ(Ω×ω+1) = ψ(Ω×ω)×ω |
ψ0(ψ1(1)+ψ0(0)) |
| ψ(Ω×ω+ψ(Ω×ω+1)) |
ψ0(ψ1(1)+ψ0(ψ1(1)+ψ0(0))) |
| ψ(Ω×ω+ψ(Ω×ω+ ψ(Ω×ω+1))) |
ψ0(ψ1(1)+ψ0(ψ1(1)+ψ0(ψ1(1)+ψ0(0)))) |
| ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+1)))) |
ψ0(ψ1(1)+ψ0(ψ1(1)+ψ0(ψ1(1)+ψ0(ψ1(1)+ψ0(0))))) |
| ψ(Ω×ω+Ω) |
ψ0(ψ1(1)+ψ1(0)) |
| ψ(Ω×ω+Ω+Ω) |
ψ0(ψ1(1)+ψ1(0)+ψ1(0)) |
| ψ(Ω×ω+Ω×ω) |
ψ0(ψ1(1)+ψ1(1)) = ψ0(ψ1(1)+ψ1(0)+ψ1(0)+...) |
| ψ(Ω×ω×ω) = ψ(Ω×ω2) |
ψ0(ψ1(2)) |
| ψ(Ω×ωω) |
ψ0(ψ1(ψ0(1))) |
| ψ(Ω×ωωω) |
ψ0(ψ1(ψ0(ψ0(1)))) |
| ψ(Ω×ωωωω) |
ψ0(ψ1(ψ0(ψ0(ψ0(1))))) |
| ψ(Ω×ψ(Ω)) = ψ(Ω×ωωω...) |
ψ0(ψ1(ψ0(ψ1(0)))) |
| ψ(Ω×ψ(Ω×2)) |
ψ0(ψ1(ψ0(ψ1(0)+ψ1(0)))) |
| ψ(Ω×ψ(Ω×ω)) |
ψ0(ψ1(ψ0(ψ1(1)))) |
| ψ(Ω×ψ(Ω×ψ(Ω))) |
ψ0(ψ1(ψ0(ψ1(ψ0(ψ1(0)))))) |
| ψ(Ω×ψ(Ω×ψ(Ω×ψ(Ω)))) |
ψ0(ψ1(ψ0(ψ1(ψ0(ψ1(ψ0(ψ1(0))))))) |
| ψ(Ω2) = ψ(Ω×Ω) |
ψ0(ψ1(ψ1(0))) |
| ψ(Ω2)+1 |
ψ0(ψ1(ψ1(0)))+ψ0(0) |
| ψ(Ω2+1) = ψ(Ω2)×ω |
ψ0(ψ1(ψ1(0))+ψ0(0)) |
| ψ(Ω2+ψ(Ω+1)) |
ψ0(ψ1(ψ1(0))+ψ0(ψ1(0)+ψ0(0))) |
| ψ(Ω2+ψ(Ω+ψ(Ω+1))) |
ψ0(ψ1(ψ1(0))+ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(0)))) |
| ψ(Ω2+Ω) |
ψ0(ψ1(ψ1(0))+ψ1(0)) |
| ψ(Ω2+Ω+Ω) |
ψ0(ψ1(ψ1(0))+ψ1(0)+ψ1(0)) |
| ψ(Ω2+Ω×ψ(Ω2+Ω)) |
ψ0(ψ1(ψ1(0))+ψ1(ψ0(ψ1(ψ1(0))+ψ1(0))))) |
| ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2+Ω))) |
ψ0(ψ1(ψ1(0))+ψ1(ψ0(ψ1(ψ1(0))+ψ1(ψ0(ψ1(ψ1(0))+ψ1(0)))))))) |
| ψ(Ω2×2) = ψ(Ω2+Ω×Ω) |
ψ0(ψ1(ψ1(0))+ψ1(ψ1(0))) |
| ψ(Ω2×3) |
ψ0(ψ1(ψ1(0))+ψ1(ψ1(0))+ψ1(ψ1(0))) |
| ψ(Ω2×ω) |
ψ0(ψ1(ψ1(0)+ψ0(0))) |
| ψ(Ω2×ψ(Ω)) |
ψ0(ψ1(ψ1(0)+ψ0(ψ1(0)))) |
| ψ(Ω2×ψ(Ω2)) |
ψ0(ψ1(ψ1(0)+ψ0(ψ1(ψ1(0))))) |
| ψ(Ω2×ψ(Ω2×ψ(Ω2))) |
ψ0(ψ1(ψ1(0)+ψ0(ψ1(ψ1(0)+ψ0(ψ1(ψ1(0))))))) |
| ψ(Ω3) = ψ(Ω2×Ω) |
ψ0(ψ1(ψ1(0)+ψ1(0))) |
| ψ(Ω3)+1 |
ψ0(ψ1(ψ1(0)+ψ1(0)))+ψ0(0) |
| ψ(Ω3+1) = ψ(Ω3)×ω |
ψ0(ψ1(ψ1(0)+ψ1(0))+ψ0(0)) |
| ψ(Ω3+ψ(Ω+1)) |
ψ0(ψ1(ψ1(0)+ψ1(0))+ψ0(ψ1(0)+ψ0(0))) |
| ψ(Ω3+ψ(Ω+ψ(Ω+1))) |
ψ0(ψ1(ψ1(0)+ψ1(0))+ψ0(ψ1(0)+ψ0(ψ1(0)+ψ0(0)))) |
| ψ(Ω3+Ω) |
ψ0(ψ1(ψ1(0)+ψ1(0))+ψ1(0)) |
| ψ(Ω3+Ω+Ω) |
ψ0(ψ1(ψ1(0)+ψ1(0))+ψ1(0)+ψ1(0)) |
| ψ(Ω3+Ω2) |
ψ0(ψ1(ψ1(0)+ψ1(0))+ψ1(ψ1(0))) |
| ψ(Ω3+Ω2+Ω2) |
ψ0(ψ1(ψ1(0)+ψ1(0))+ψ1(ψ1(0))+ψ1(ψ1(0))) |
| ψ(Ω3+Ω2×ψ(Ω3+Ω2)) |
ψ0(ψ1(ψ1(0)+ψ1(0))+ψ1(ψ1(0)+ψ0(ψ1(ψ1(0)+ψ1(0))+ψ1(ψ1(0))))) |
| ψ(Ω3+Ω2×ψ(Ω3+Ω2×ψ(Ω3+Ω2))) |
ψ0(ψ1(ψ1(0)+ψ1(0))+ψ1(ψ1(0)+ψ0(ψ1(ψ1(0)+ψ1(0))+ψ1(ψ1(0)+
ψ0(ψ1(ψ1(0)+ψ1(0))+ψ1(ψ1(0))))))) |
| ψ(Ω3×2) = ψ(Ω3+Ω2×Ω) |
ψ0(ψ1(ψ1(0)+ψ1(0))+ψ1(ψ1(0)+ψ1(0))) |
| ψ(Ω3×3) |
ψ0(ψ1(ψ1(0)+ψ1(0))+ψ1(ψ1(0)+ψ1(0))+ψ1(ψ1(0)+ψ1(0))) |
| ψ(Ω3×ω) |
ψ0(ψ1(ψ1(0)+ψ1(0)+ψ0(0))) |
| ψ(Ω3×ψ(Ω)) |
ψ0(ψ1(ψ1(0)+ψ1(0)+ψ0(ψ1(0)))) |
| ψ(Ω3×ψ(Ω2)) |
ψ0(ψ1(ψ1(0)+ψ1(0)+ψ0(ψ1(ψ1(0))))) |
| ψ(Ω3×ψ(Ω3)) |
ψ0(ψ1(ψ1(0)+ψ1(0)+ψ0(ψ1(ψ1(0)+ψ1(0))))) |
| ψ(Ω4) |
ψ0(ψ1(ψ1(0)+ψ1(0)+ψ1(0))) |
| ψ(Ω5) |
ψ0(ψ1(ψ1(0)+ψ1(0)+ψ1(0)+ψ1(0))) |
| ψ(Ωω) |
ψ0(ψ1(ψ1(1))) |
| ψ(Ωω+1) = ψ(Ωω)×ω |
ψ0(ψ1(ψ1(1))+ψ0(0))) |
| ψ(Ωω+Ω) |
ψ0(ψ1(ψ1(1))+ψ1(0))) |
| ψ(Ωω+Ω2) |
ψ0(ψ1(ψ1(1))+ψ1(ψ1(0)))) |
| ψ(Ωω+Ω3) |
ψ0(ψ1(ψ1(1))+ψ1(ψ1(0)+ψ1(0)))) |
| ψ(Ωω×2) = ψ(Ωω+Ωω) |
ψ0(ψ1(ψ1(1))+ψ1(ψ1(1))) = ψ0(ψ1(ψ1(1))+ψ1(ψ1(0)+ψ1(0)+ψ1(0)+...))) |
| ψ(Ωω×ω) = ψ(Ωω×ψ(1)) |
ψ0(ψ1(ψ1(1)+ψ0(0))) = ψ0(ψ1(ψ1(1))+ψ1(ψ1(1))+ψ1(ψ1(1))+...) |
| ψ(Ωω×ω+Ωω) |
ψ0(ψ1(ψ1(1)+ψ0(0))+ψ1(ψ1(1))) |
| ψ(Ωω×ω+Ωω×ω) |
ψ0(ψ1(ψ1(1)+ψ0(0)+ψ0(0))) |
| ψ(Ωω×ω2) |
ψ0(ψ1(ψ1(1)+ψ0(ψ0(0)))) |
| ψ(Ωω×ωω) |
ψ0(ψ1(ψ1(1)+ψ0(ψ0(1)))) |
| ψ(Ωω×ε0) = ψ(Ωω×ψ(Ω)) |
ψ0(ψ1(ψ1(1)+ψ0(ψ1(0)))) |
| ψ(Ωω×ζ0) = ψ(Ωω×ψ(Ω2)) |
ψ0(ψ1(ψ1(1)+ψ0(ψ1(ψ1(0))))) |
| ψ(Ωω×η0) = ψ(Ωω×ψ(Ω3)) |
ψ0(ψ1(ψ1(1)+ψ0(ψ1(ψ1(0)+ψ1(0))))) |
| ψ(Ωω×ψ(Ωω)) |
ψ0(ψ1(ψ1(1)+ψ0(ψ1(ψ1(1))))) |
| ψ(Ωω×ψ(Ωω×ψ(Ωω))) |
ψ0(ψ1(ψ1(1)+ψ0(ψ1(ψ1(1)+ψ0(ψ1(ψ1(1))))))) |
| ψ(Ωω+1) = ψ(Ωω×Ω) |
ψ0(ψ1(ψ1(1)+ψ1(0))) |
| ψ(Ωω+2) |
ψ0(ψ1(ψ1(1)+ψ1(0)+ψ1(0))) |
| ψ(Ωω+3) |
ψ0(ψ1(ψ1(1)+ψ1(0)+ψ1(0)+ψ1(0))) |
| ψ(Ωω×2) |
ψ0(ψ1(ψ1(1)+ψ1(1))) |
| ψ(Ωω×3) |
ψ0(ψ1(ψ1(1)+ψ1(1)+ψ1(1))) |
| ψ(Ωω2) |
ψ0(ψ1(ψ1(2))) |
| ψ(Ωω3) |
ψ0(ψ1(ψ1(3))) |
| ψ(Ωωω) |
ψ0(ψ1(ψ1(ψ0(1)))) |
| ψ(Ωωωω) |
ψ0(ψ1(ψ1(ψ0(ψ0(1))))) |
| ψ(Ωωωωω) |
ψ0(ψ1(ψ1(ψ0(ψ0(ψ0(1)))))) |
| ψ(Ωωωωωω) |
ψ0(ψ1(ψ1(ψ0(ψ0(ψ0(ψ0(1))))))) |
| ψ(Ωψ(Ω)) |
ψ0(ψ1(ψ1(ψ0(ψ1(0))))) |
| ψ(Ωψ(Ω2)) |
ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(0)))))) |
| ψ(Ωψ(Ω3)) |
ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(0)+ψ1(0)))))) |
| ψ(Ωψ(Ω4)) |
ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(0)+ψ1(0)+ψ1(0)))))) |
| ψ(Ωψ(Ωω)) |
ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(1)))))) |
| ψ(Ωψ(Ωψ(Ω))) |
ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(ψ0(ψ1(0)))))))) |
| ψ(Ωψ(Ωψ(Ωψ(Ω)))) |
ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(ψ0(ψ1(0))))))))))) |
| ψ(Ωψ(Ωψ(Ωψ(Ωψ(Ω))))) |
ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(ψ0(ψ1(0)))))))))))))) |
| ψ(ΩΩ) = ψ(Ωψ(Ωψ(Ωψ(Ωψ(...))))) |
ψ0(ψ1(ψ1(ψ1(0)))) = ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(...))))))))) |
| ψ(ΩΩ)+1 |
ψ0(ψ1(ψ1(ψ1(0))))+ψ0(0) |
| ψ(ΩΩ+1) = ψ(ΩΩ)×ω |
ψ0(ψ1(ψ1(ψ1(0)))+ψ0(0)) |
| ψ(ΩΩ+ψ(ΩΩ+1)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ0(ψ1(ψ1(ψ1(0)))+ψ0(0))) |
| ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ+1))) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ0(ψ1(ψ1(ψ1(0)))+ψ0(ψ1(ψ1(ψ1(0)))+ψ0(0)))) |
| ψ(ΩΩ+Ω) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(0)) |
| ψ(ΩΩ+Ω2) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(0))) |
| ψ(ΩΩ+Ω3) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(0)+ψ1(0))) |
| ψ(ΩΩ+Ωω) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(1))) |
| ψ(ΩΩ+Ωψ(Ωω)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(1)))))) |
| ψ(ΩΩ+Ωψ(Ωψ(Ωω))) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(1))))))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)+1) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))))+ψ0(0)) |
| ψ(ΩΩ+Ωψ(ΩΩ)+Ω) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))))+ψ1(0)) |
| ψ(ΩΩ+Ωψ(ΩΩ)+Ω2) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))))+ψ1(ψ1(0))) |
| ψ(ΩΩ+Ωψ(ΩΩ)+Ω3) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))))+ψ1(ψ1(0)+ψ1(0))) |
| ψ(ΩΩ+Ωψ(ΩΩ)+Ωω) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))))+ψ1(ψ1(1))) |
| ψ(ΩΩ+Ωψ(ΩΩ)+Ωψ(Ωω)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))))+
ψ1(ψ1(ψ0(ψ1(ψ1(1)))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)+Ωψ(Ωψ(Ωω))) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))))+
ψ1(ψ1(ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(1)))))))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×2) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))))+
ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×ω) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+ψ0(0))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×ψ(Ω)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+ψ0(ψ1(0)))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×ψ(Ω2)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+ψ0(ψ1(ψ1(0))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×ψ(Ω3)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+ψ0(ψ1(ψ1(0)+ψ1(0))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×ψ(Ωω)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+ψ0(ψ1(ψ1(1))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×ψ(Ωψ(Ωω))) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+
ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(1)))))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×ψ(Ωψ(Ωψ(Ωω)))) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+
ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(ψ0(ψ1(ψ1(1))))))))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+ψ0(ψ1(ψ1(ψ1(0)))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×(ψ(ΩΩ)+1)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+
ψ0(ψ1(ψ1(ψ1(0)))))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+1))) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+
ψ0(ψ1(ψ1(ψ1(0)))+ψ0(0)))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ω))) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(0)))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ωψ(ΩΩ)))) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+
ψ0(ψ1(ψ1(ψ1(0)))))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ωψ(ΩΩ))))) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))+
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))))))))) |
| ψ(ΩΩ+Ωψ(ΩΩ)+1) = ψ(ΩΩ+Ωψ(ΩΩ)×Ω) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))+ψ0(0)))) |
| ψ(ΩΩ+Ωψ(ΩΩ)+1×2) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))+
ψ0(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))+ψ0(0)))) |
| ψ(ΩΩ+Ωψ(ΩΩ)+2) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))+ψ0(0)+ψ0(0)))) |
| ψ(ΩΩ+Ωψ(ΩΩ+1)) = ψ(ΩΩ+Ωψ(ΩΩ)×ω) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))+ψ0(0))))) |
| ψ(ΩΩ+Ωψ(ΩΩ+Ω)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))+ψ1(0))))) |
| ψ(ΩΩ+Ωψ(ΩΩ+Ω2)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(0)))))) |
| ψ(ΩΩ+Ωψ(ΩΩ+Ω3)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(0)+ψ1(0)))))) |
| ψ(ΩΩ+Ωψ(ΩΩ+Ωω)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(1)))))) |
| ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))+
ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))))))) |
| ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)+1)) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))+
ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))+ψ0(0))))))) |
| ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)))) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))+
ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))))))))))) |
| ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)+1))) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))+
ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0))))+ψ0(0)))))))))) |
| ψ(ΩΩ×2) = ψ(ΩΩ+ΩΩ) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ1(0)))) |
| ψ(ΩΩ×3) |
ψ0(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ1(0)))) |
| ψ(ΩΩ×ω) |
ψ0(ψ1(ψ1(ψ1(0))+ψ0(0))) |
| ψ(ΩΩ×ψ(Ω)) |
ψ0(ψ1(ψ1(ψ1(0))+ψ0(ψ1(0)))) |
| ψ(ΩΩ×ψ(ΩΩ)) |
ψ0(ψ1(ψ1(ψ1(0))+ψ0(ψ1(ψ1(ψ1(0)))))) |
| ψ(ΩΩ×ψ(ΩΩ×ψ(ΩΩ)) |
ψ0(ψ1(ψ1(ψ1(0))+ψ0(ψ1(ψ1(ψ1(0))+ψ0(ψ1(ψ1(ψ1(0)))))))) |
| ψ(ΩΩ×Ω) = ψ(ΩΩ+1) |
ψ0(ψ1(ψ1(ψ1(0))+ψ1(0))) |
| ψ(ΩΩ+1×2) |
ψ0(ψ1(ψ1(ψ1(0))+ψ1(0))+ψ1(ψ1(ψ1(0))+ψ1(0))) |
| ψ(ΩΩ+2) |
ψ0(ψ1(ψ1(ψ1(0))+ψ1(0)+ψ1(0))) |
| ψ(ΩΩ+ω) |
ψ0(ψ1(ψ1(ψ1(0))+ψ1(1))) |
| ψ(ΩΩ+ψ(Ω)) |
ψ0(ψ1(ψ1(ψ1(0))+ψ1(ψ0(ψ1(0))))) |
| ψ(ΩΩ+ψ(ΩΩ)) |
ψ0(ψ1(ψ1(ψ1(0))+ψ1(ψ0(ψ1(ψ1(ψ1(0)))))) |
| ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ))) |
ψ0(ψ1(ψ1(ψ1(0))+ψ1(ψ0(ψ1(ψ1(ψ1(0))+ψ1(ψ0(ψ1(ψ1(ψ1(0)))))))))) |
| ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ)))) |
ψ0(ψ1(ψ1(ψ1(0))+ψ1(ψ0(ψ1(ψ1(ψ1(0))+ψ1(ψ0(ψ1(ψ1(ψ1(0))+
ψ1(ψ0(ψ1(ψ1(ψ1(0))))))))))))) |
| ψ(ΩΩ×2) = ψ(ΩΩ+Ω) |
ψ0(ψ1(ψ1(ψ1(0))+ψ1(ψ1(0)))) |
| ψ(ΩΩ×2×2) |
ψ0(ψ1(ψ1(ψ1(0))+ψ1(ψ1(0)))+ψ1(ψ1(ψ1(0))+ψ1(ψ1(0)))) |
| ψ(ΩΩ×2×Ω) = ψ(ΩΩ×2+1) |
ψ0(ψ1(ψ1(ψ1(0))+ψ1(ψ1(0))+ψ0(0))) |
| ψ(ΩΩ×3) |
ψ0(ψ1(ψ1(ψ1(0))+ψ1(ψ1(0))+ψ1(ψ1(0)))) |
| ψ(ΩΩ×ω) |
ψ0(ψ1(ψ1(ψ1(0)+ψ0(0)))) |
| ψ(ΩΩ×ω2) |
ψ0(ψ1(ψ1(ψ1(0)+ψ0(1)))) |
| ψ(ΩΩ×ωω) |
ψ0(ψ1(ψ1(ψ1(0)+ψ0(ψ0(1))))) |
| ψ(ΩΩ×ψ(Ω)) |
ψ0(ψ1(ψ1(ψ1(0)+ψ0(ψ1(0))))) |
| ψ(ΩΩ×ψ(ΩΩ)) |
ψ0(ψ1(ψ1(ψ1(0)+ψ0(ψ1(ψ1(ψ1(0))))))) |
| ψ(ΩΩ×ψ(ΩΩ×ψ(ΩΩ))) |
ψ0(ψ1(ψ1(ψ1(0)+ψ0(ψ1(ψ1(ψ1(0)+ψ0(ψ1(ψ1(ψ1(0)))))))))) |
| ψ(ΩΩ×ψ(ΩΩ×ψ(ΩΩ×ψ(ΩΩ)))) |
ψ0(ψ1(ψ1(ψ1(0)+ψ0(ψ1(ψ1(ψ1(0)+ψ0(ψ1(ψ1(ψ1(0)+
ψ0(ψ1(ψ1(ψ1(0)))))))))) |
| ψ(ΩΩ2) = ψ(ΩΩ×Ω) |
ψ0(ψ1(ψ1(ψ1(0)+ψ1(0)))) |
| ψ(ΩΩ3) |
ψ0(ψ1(ψ1(ψ1(0)+ψ1(0)+ψ1(0)))) |
| ψ(ΩΩω) |
ψ0(ψ1(ψ1(ψ1(1)))) = ψ0(ψ1(ψ1(ψ1(0)+ψ1(0)+ψ1(0)+ψ1(0)+...))) |
| ψ(ΩΩω+1) |
ψ0(ψ1(ψ1(ψ1(1)+ψ1(0)))) |
| ψ(ΩΩω×2) |
ψ0(ψ1(ψ1(ψ1(1)+ψ1(1)))) |
| ψ(ΩΩω2) |
ψ0(ψ1(ψ1(ψ1(2)))) |
| ψ(ΩΩωω) |
ψ0(ψ1(ψ1(ψ1(ψ0(1))))) |
| ψ(ΩΩψ(Ω)) |
ψ0(ψ1(ψ1(ψ1(ψ0(ψ1(0)))))) |
| ψ(ΩΩψ(ΩΩ)) |
ψ0(ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))))) |
| ψ(ΩΩψ(ΩΩω)) |
ψ0(ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(1)))))))) |
| ψ(ΩΩψ(ΩΩψ(ΩΩ))) |
ψ0(ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))))))))) |
| ψ(ΩΩψ(ΩΩψ(ΩΩω))) |
ψ0(ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(1)))))))))))) |
| ψ(ΩΩΩ) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))) |
| ψ(ΩΩΩ+1) = ψ(ΩΩΩ)×ω |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ0(0)) |
| ψ(ΩΩΩ+ψ(ΩΩΩ)) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ0(ψ1(ψ1(ψ1(ψ1(0)))))) |
| ψ(ΩΩΩ+ψ(ΩΩΩ+1)) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ0(0))) |
| ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ))) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ0(ψ1(ψ1(ψ1(ψ1(0))))+
ψ0(ψ1(ψ1(ψ1(ψ1(0))))))) |
| ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ+1))) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ0(ψ1(ψ1(ψ1(ψ1(0))))+
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ0(0)))) |
| ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ)))) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ0(ψ1(ψ1(ψ1(ψ1(0))))+
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ0(ψ1(ψ1(ψ1(ψ1(0)))))))) |
| ψ(ΩΩΩ+Ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(0)) |
| ψ(ΩΩΩ+Ω2) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(0))) |
| ψ(ΩΩΩ+Ω3) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(0)+ψ1(0))) |
| ψ(ΩΩΩ+ΩΩ) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(0)))) |
| ψ(ΩΩΩ+ΩΩ×2) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(0))+ψ1(ψ1(0)))) |
| ψ(ΩΩΩ+ΩΩ×3) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ ψ1(ψ1(ψ1(0))+ψ1(ψ1(0))+ψ1(ψ1(0)))) |
| ψ(ΩΩΩ+ΩΩ2) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(0)+ψ1(0)))) |
| ψ(ΩΩΩ+ΩΩ3) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(0)+ψ1(0)+ψ1(0)))) |
| ψ(ΩΩΩ+ΩΩω) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(1)))) |
| ψ(ΩΩΩ+ΩΩψ(Ω)) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(ψ0(ψ1(0)))))) |
| ψ(ΩΩΩ+ΩΩψ(ΩΩ)) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(0)))))))) |
| ψ(ΩΩΩ+ΩΩψ(ΩΩω)) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(1)))))))) |
| ψ(ΩΩΩ+ΩΩψ(ΩΩψ(ΩΩω))) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+
ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(1)))))))))))) |
| ψ(ΩΩΩ+ΩΩψ(ΩΩΩ)) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(0))))))))) |
| ψ(ΩΩΩ+ΩΩψ(ΩΩΩ+ΩΩω)) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(0))))+
ψ1(ψ1(ψ1(1)))))))) |
| ψ(ΩΩΩ+ΩΩψ(ΩΩΩ+ΩΩψ(ΩΩΩ))) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(0))))+
ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(0))))))))))))) |
| ψ(ΩΩΩ+ΩΩψ(ΩΩΩ+ΩΩψ(ΩΩΩ+ΩΩω))) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(0))))+
ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(1)))))))))))) |
| ψ(ΩΩΩ×2) = ψ(ΩΩΩ+ΩΩΩ) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(ψ1(0))))) |
| ψ(ΩΩΩ×3) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(ψ1(0))))+ψ1(ψ1(ψ1(ψ1(0))))) |
| ψ(ΩΩΩ×ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)))+ψ0(0))) |
| ψ(ΩΩΩ×ψ(ΩΩΩ)) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)))+ψ0(ψ1(ψ1(ψ1(ψ1(0))))))) |
| ψ(ΩΩΩ×ψ(ΩΩΩ×ψ(ΩΩΩ))) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)))+ψ0(ψ1(ψ1(ψ1(ψ1(0)))+
ψ0(ψ1(ψ1(ψ1(ψ1(0))))))))) |
| ψ(ΩΩΩ+1) = ψ(ΩΩΩ×Ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)))+ψ1(0))) |
| ψ(ΩΩΩ+2) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)))+ψ1(0)+ψ1(0))) |
| ψ(ΩΩΩ+ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)))+ψ1(1))) |
| ψ(ΩΩΩ+ψ(ΩΩ)) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)))+ψ1(ψ0(ψ1(ψ1(ψ1(0))))))) |
| ψ(ΩΩΩ+ψ(ΩΩΩ)) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)))+ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(0)))))))) |
| ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ))) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)))+ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(0)))+
ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(0)))))))) |
| ψ(ΩΩΩ+Ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(0)))) |
| ψ(ΩΩΩ+Ω2) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ1(0))))) |
| ψ(ΩΩΩ×2) = (ΩΩΩ+ΩΩ) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ1(ψ1(0)))))) |
| ψ(ΩΩΩ×3) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)))+ψ1(ψ1(ψ1(ψ1(0)))))+ψ1(ψ1(ψ1(ψ1(0)))))) |
| ψ(ΩΩΩ×ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))+ψ0(0)))) |
| ψ(ΩΩΩ×ω2) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))+ψ0(1)))) |
| ψ(ΩΩΩ×ψ(ΩΩΩ)) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))+ψ0(ψ1(ψ1(ψ1(ψ1(0)))))))) |
| ψ(ΩΩΩ×ψ(ΩΩΩ×ψ(ΩΩΩ))) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))+ψ0(ψ1(ψ1(ψ1(ψ1(0))+
ψ0(ψ1(ψ1(ψ1(ψ1(0))))))))))) |
| ψ(ΩΩΩ+1) = ψ(ΩΩΩ×Ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))+ψ1(0)))) |
| ψ(ΩΩΩ+2) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))+ψ1(0)+ψ1(0)))) |
| ψ(ΩΩΩ+ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))+ψ1(1)))) |
| ψ(ΩΩΩ+ψ(ΩΩΩ)) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))+ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(0))))))))) |
| ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ))) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))+ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(0))+
ψ0(ψ1(ψ1(ψ1(ψ1(0)))))))))))) |
| ψ(ΩΩΩ×2) = ψ(ΩΩΩ+Ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))+ψ1(ψ1(0))))) |
| ψ(ΩΩΩ×3) |
ψ0(ψ1(ψ1(ψ1(ψ1(0))+ψ1(ψ1(0))+ψ1(ψ1(0))))) |
| ψ(ΩΩΩ×ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)+ψ0(0))))) = ψ0(ψ1(ψ1(ψ1(ψ1(0))+ψ1(ψ1(0))+ψ1(ψ1(0))+ψ1(ψ1(0))+...))) |
| ψ(ΩΩΩ×ψ(ΩΩΩ)) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)+ψ0(ψ1(ψ1(ψ1(ψ1(0))))))))) |
| ψ(ΩΩΩ×ψ(ΩΩΩ×ψ(ΩΩΩ))) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)+ψ0(ψ1(ψ1(ψ1(ψ1(0)+
ψ0(ψ1(ψ1(ψ1(ψ1(0))))))))))))) |
| ψ(ΩΩΩ2) = ψ(ΩΩΩ×Ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)+ψ1(0))))) |
| ψ(ΩΩΩ2+1) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)+ψ1(0))+ψ0(0)))) |
| ψ(ΩΩΩ2+Ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)+ψ1(0))+ψ1(0)))) |
| ψ(ΩΩΩ2×2) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)+ψ1(0))+ψ1(ψ1(0)+ψ1(0))))) |
| ψ(ΩΩΩ3) |
ψ0(ψ1(ψ1(ψ1(ψ1(0)+ψ1(0)+ψ1(0))))) |
| ψ(ΩΩΩω) |
ψ0(ψ1(ψ1(ψ1(ψ1(1))))) |
| ψ(ΩΩΩω2) |
ψ0(ψ1(ψ1(ψ1(ψ1(2))))) |
| ψ(ΩΩΩψ(ΩΩΩ)) |
ψ0(ψ1(ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(0)))))))))) |
| ψ(ΩΩΩψ(ΩΩΩω)) |
ψ0(ψ1(ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(1)))))))))) |
| ψ(ΩΩΩψ(ΩΩΩψ(ΩΩΩ))) |
ψ0(ψ1(ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(ψ0(ψ1(ψ1(ψ1(ψ1(0))))))))))))))) |
| ψ(ΩΩΩΩ) |
ψ0(ψ1(ψ1(ψ1(ψ1(ψ1(0)))))) |
| ψ(ΩΩΩΩ×ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(ψ1(0)+ψ0(0)))))) |
| ψ(ΩΩΩΩ2) |
ψ0(ψ1(ψ1(ψ1(ψ1(ψ1(0)+ψ1(0)))))) |
| ψ(5Ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(0))))))) |
| ψ(6Ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(0)))))))) |
| ψ(7Ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(0))))))))) |
| ψ(8Ω) |
ψ0(ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(0)))))))))) |
| ψ(ωΩ) = ψ(εΩ+1) = ψ(φ(1,Ω+1)) |
ψ(Ω2) = ψ0(ψ1(Ω2)) = ψ0(ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(ψ1(...)))))))) |
| ψ(εΩ+1)+1 |
ψ(Ω2)+1 |
| ψ(εΩ+1)×2 |
ψ(Ω2)×2 |
| ψ(εΩ+1)×ω = ψ(εΩ+1+1) = ψ(ΩΩΩΩ...+1) |
ψ(Ω2+1) = ψ(Ω2)×ω |
| ψ(εΩ+1)2 = ψ(εΩ+1+ψ(εΩ+1)) |
ψ(Ω2+ψ(Ω2)) |
| ψ(εΩ+1)ω = ψ(εΩ+1+ψ(εΩ+1+1)) |
ψ(Ω2+ψ(Ω2+1)) |
| ψ(εΩ+1)ψ(εΩ+1) = ψ(εΩ+1+ψ(εΩ+1+ψ(εΩ+1))) |
ψ(Ω2+ψ(Ω2+ψ(Ω2))) |
| ψ(εΩ+1)ψ(εΩ+1)ω = ψ(εΩ+1+ψ(εΩ+1+ψ(εΩ+1+1))) |
ψ(Ω2+ψ(Ω2+ψ(Ω2+1))) |
| ψ(εΩ+1)ψ(εΩ+1)ψ(εΩ+1) = ψ(εΩ+1+ψ(εΩ+1+ψ(εΩ+1+ψ(εΩ+1)))) |
ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2)))) |
| ψ(εΩ+1)ψ(εΩ+1)ψ(εΩ+1)...= εψ(εΩ+1)+1 = φ(1,ψ(εΩ+1)+1) = ψ(εΩ+1+ψ(εΩ+1+ψ(εΩ+1+ψ(...)))) = ψ(εΩ+1+Ω) |
ψ(Ω2+Ω) = ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(...))))) |
| ζψ(εΩ+1)+1 = φ(2,ψ(εΩ+1)+1) = ψ(εΩ+1+Ω2) |
ψ(Ω2+Ω2) |
| ηψ(εΩ+1)+1 = φ(3,ψ(εΩ+1)+1) = ψ(εΩ+1+Ω3) |
ψ(Ω2+Ω3) |
| Гψ(εΩ+1)+1 = φ(1,0,ψ(εΩ+1)+1) = ψ(εΩ+1+ΩΩ) |
ψ(Ω2+ΩΩ) |
| ψ(εΩ+1+ΩΩΩ) |
ψ(Ω2+ΩΩΩ) |
| ψ(εΩ+1+ΩΩΩΩ...) = ψ(εΩ+1×2) |
ψ(Ω2+ψ1(Ω2)) |
| ψ(εΩ+1×ω) = ψ(ωεΩ+1+1) |
ψ(Ω2+ψ1(Ω2+1)) |
| ψ(εΩ+1×ψ(εΩ+1)) |
ψ(Ω2+ψ1(Ω2+ψ(Ω2)) |
| ψ(εΩ+1×ψ(εΩ+1×...)) = ψ(εΩ+1×Ω) = ψ(ΩΩΩΩ...+1) |
ψ(Ω2+ψ1(Ω2+Ω)) = ψ(Ω2+ψ1(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+...))))) |
| ψ(εΩ+1×Ωω) |
ψ(Ω2+ψ1(Ω2+Ωω)) |
| ψ(εΩ+1×ΩΩ) |
ψ(Ω2+ψ1(Ω2+ΩΩ)) |
| ψ(εΩ+1×ΩΩΩΩ...) = ψ(εΩ+12) = ψ(ωεΩ+1×2) |
ψ(Ω2+ψ1(Ω2+ψ1(Ω2))) |
| ψ(εΩ+1ω) = ψ(ωεΩ+1×ω) = ψ(ωωεΩ+1+1) |
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+1))) |
| ψ(εΩ+1ψ(εΩ+1ψ(εΩ+1...))) = ψ(εΩ+1Ω) = ψ(ΩΩΩΩ...+1) = ψ(ωωεΩ+1+Ω) |
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+Ω))) |
| ψ(εΩ+1ΩΩΩ...) =ψ(εΩ+1εΩ+1) = ψ(ωωεΩ+1+εΩ+1) = ψ(ωωεΩ+1×2) |
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2)))) |
| ψ(εΩ+1εΩ+1ω) = ψ(ωωωεΩ+1+1) |
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+1)))) |
| ψ(εΩ+1εΩ+1Ω) = ψ(ΩΩΩΩ...+1) = ψ(ωωεΩ+1×Ω) |
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+Ω)))) |
| ψ(εΩ+1εΩ+1εΩ+1) = ψ(ωωεΩ+12) = ψ(ωωωεΩ+1×2) |
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2))))) |
| ψ(εΩ+1εΩ+1εΩ+1εΩ+1) = ψ(ωωωεΩ+12) = ψ(ωωωωεΩ+1×2) |
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2)))))) |
| ψ(εΩ+1εΩ+1εΩ+1εΩ+1εΩ+1) = ψ(ωωωωεΩ+12) = ψ(ωωωωωεΩ+1×2) |
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2)))))))) |
| ψ(εΩ+2) = ψ(εΩ+1εΩ+1εΩ+1...) = ψ(ωωω...εΩ+1) = ψ(ΩΩΩ...εΩ+1) |
ψ(Ω2×2) = ψ(Ω2+Ω2) = ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+...)))) |
| ψ(εΩ+3) = ψ(εΩ+2εΩ+2εΩ+2...) = ψ(ωωω...εΩ+2) = ψ(ΩΩΩ...εΩ+2) |
ψ(Ω2×3) |
| ψ(εΩ+ω) |
ψ(Ω2×ω) |
| ψ(εΩ×2) = ψ(εΩ+Ω) = ψ(εΩ+ψ(εΩ+ψ(εΩ+...))) |
ψ(Ω2×Ω) |
| ψ(εΩ2) = ψ(εΩ×Ω) = ψ(εΩ×ψ(εΩ×ψ(εΩ×...))) |
ψ(Ω2×Ω2) |
| ψ(εΩΩ)= ψ(εΩψ(εΩψ(εΩ...))) |
ψ(Ω2×ΩΩ) |
| ψ(εεΩ+1) = ψ(εΩΩΩΩ...) |
ψ(Ω2×ψ1(Ω2)) |
| ψ(εεεΩ+1) = ψ(εεΩΩΩΩ...) |
ψ(Ω2×ψ1(Ω2×ψ1(Ω2))) |
| ψ(ζΩ+1) = ψ(εεε...Ω+1) = ψ(φ(2,Ω+1)) |
ψ(Ω22) = ψ(Ω2×Ω2) = ψ(Ω2×ψ1(Ω2×ψ1(Ω2×ψ1(Ω2×...)))) |
| ψ(ζΩ+2) = ψ(εεε...ζΩ+1+1) = ψ(φ(2,Ω+2)) |
ψ(Ω22×2) |
| ψ(ηΩ+1) = ψ(ζζζ...Ω+1) = ψ(φ(3,Ω+1)) |
ψ(Ω23) |
| ψ(ηΩ+2) = ψ(ζζζ...ηΩ+1+1) = ψ(φ(3,Ω+2)) |
ψ(Ω23×2) |
| ψ(φ(ω,Ω+1)) |
ψ(Ω2ω) |
| ψ(φ(ω,φ(ω,Ω+1))) |
ψ(Ω2ω×ψ1(Ω2ω)) |
| ψ(φ(ω,φ(ω,φ(ω,Ω+1)))) |
ψ(Ω2ω×ψ1(Ω2ω×ψ1(Ω2ω))) |
| ψ(φ(ω+1,Ω+1)) = ψ(φ(ω,φ(ω,φ(ω,...φ(ω,Ω+1)...)))) |
ψ(Ω2ω+1) = ψ(Ω2ω×ψ1(Ω2ω×ψ1(Ω2ω×ψ1(...)))) |
| ψ(φ(ω2,Ω+1)) |
ψ(Ω2ω2) |
| ψ(φ(Г0,Ω+1)) = ψ(φ(φ(φ(φ(...,0),0),0),Ω+1)) = ψ(φ(ψ(ΩΩ),Ω+1)) |
ψ(Ω2ψ(ΩΩ)) |
| ψ(φ(ψ(φ(1,Ω+1)),Ω+1)) = φ(ψ(εΩ+1),Ω+1)) = ψ(φ(ψ(ΩΩΩΩ...),Ω+1)) |
ψ(Ω2ψ(Ω2)) |
| ψ(φ(ψ(φ(ω,Ω+1)),Ω+1)) |
ψ(Ω2ψ(Ω2ω)) |
| ψ(φ(ψ(φ(ψ(φ(ω,Ω+1)),Ω+1)),Ω+1)) |
ψ(Ω2ψ(Ω2ψ(Ω2ω))) |
| ψ(φ(ψ(φ(ψ(φ(ψ(φ(ω,Ω+1)),Ω+1)),Ω+1)),Ω+1)) |
ψ(Ω2ψ(Ω2ψ(Ω2ψ(Ω2ω)))) |
| ψ(φ(Ω,1)) = ψ(φ(ψ(φ(ψ(φ(ψ(φ(...,Ω+1)),Ω+1)),Ω+1)),Ω+1)) |
ψ(Ω2Ω) |
| ψ(φ(Ω,2)) = ψ(φ(ψ(φ(ψ(φ(...ψ(φ(Ω,1))...,Ω+1)),Ω+1)),Ω+1)) |
ψ(Ω2Ω×2) |
| ψ(φ(Ω,Ω)) = ψ(φ(Ω,ψ(φ(Ω,ψ(φ(Ω,...)))))) |
ψ(Ω2Ω×Ω) = ψ(Ω2Ω×ψ(Ω2Ω×ψ(Ω2Ω×...))) |
| ψ(φ(Ω+1,0)) = ψ(φ(Ω,φ(Ω,φ(Ω,φ(Ω,...))))) |
ψ(Ω2Ω+1) = ψ(Ω2Ω×Ω2) = ψ(Ω2Ω×ψ1(Ω2Ω×ψ1(Ω2Ω×ψ1(Ω2Ω×...)))) |
| ψ(φ(εΩ+1,0)) |
ψ(Ω2ψ1(Ω2)) = ψ(Ω2εΩ+1) |
| ψ(φ(φ(Ω,1),0)) |
ψ(Ω2ψ1(Ω2Ω)) |
| ψ(φ(φ(φ(Ω,1),0),0)) |
ψ(Ω2ψ1(Ω2ψ1(Ω2Ω))) |
| ψ(φ(φ(φ(φ(Ω,1),0),0),0)) |
ψ(Ω2ψ1(Ω2ψ1(Ω2ψ1(Ω2Ω)))) |
| ψ(ГΩ+1) = ψ(φ(1,0,Ω+1)) = ψ(φ(φ(φ(...φ(Ω,1)...,0),0),0)) |
ψ(Ω2Ω2) = ψ(Ω2ψ1(Ω2ψ1(Ω2ψ1(Ω2ψ1(...))))) |
| ψ(ГΩ+2) = ψ(φ(1,0,Ω+2)) |
ψ(Ω2Ω2×2) |
| ψ(φ(1,0,Ω+φ(1,0,Ω+1))) |
ψ(Ω2Ω2×ψ(Ω2Ω2)) |
| ψ(φ(1,0,Ω×2)) = ψ(φ(1,0,Ω+φ(1,0,Ω+φ(1,0,Ω+...)))) |
ψ(Ω2Ω2×Ω) |
| ψ(φ(1,0,φ(1,Ω+1))) |
ψ(Ω2Ω2×ψ1(Ω2)) |
| ψ(φ(1,0,φ(1,0,Ω+1))) |
ψ(Ω2Ω2×ψ1(Ω2Ω2)) |
| ψ(φ(1,1,Ω+1)) = ψ(φ(1,0,φ(1,0,φ(1,0,...φ(1,0,Ω+1)...)))) |
ψ(Ω2Ω2×Ω2) = ψ(Ω2Ω2+1) |
| ψ(φ(1,Ω,1)) = ψ(φ(1,ψ(φ(1,ψ(φ(1,ψ(φ(1,...,Ω+1),Ω+1)),Ω+1)),Ω+1)) |
ψ(Ω2Ω2+Ω) |
| ψ(φ(1,φ(1,Ω,1),0)) |
ψ(Ω2Ω2+ψ1(Ω2Ω2)) |
| ψ(φ(1,φ(1,φ(1,Ω,1),0),0)) |
ψ(Ω2Ω2+ψ1(Ω2Ω2+ψ1(Ω2Ω2))) |
| ψ(φ(1,φ(1,φ(1,φ(1,Ω,1),0),0),0)) |
ψ(Ω2Ω2+ψ1(Ω2Ω2+ψ1(Ω2Ω2+ψ1(Ω2Ω2)))) |
| ψ(φ(2,0,Ω+1)) = ψ(φ(1,φ(1,φ(1,...φ(1,Ω,1)...,0),0),0)) |
ψ(Ω2Ω2×2) = ψ(Ω2Ω2+Ω2) |
| ψ(φ(3,0,Ω+1)) |
ψ(Ω2Ω2×3) |
| ψ(φ(ω,0,Ω+1)) |
ψ(Ω2Ω2×ω) |
| ψ(φ(ψ(φ(ω,0,Ω+1)),0,Ω+1)) |
ψ(Ω2Ω2×ψ(Ω2Ω2)) |
| ψ(φ(Ω,0,1)) = ψ(φ(ψ(φ(ψ(φ(...,0,Ω+1)),0,Ω+1)),0,Ω+1)) |
ψ(Ω2Ω2×Ω) |
| ψ(φ(φ(Ω,0,1),0,0)) |
ψ(Ω2Ω2×ψ1(Ω2Ω2)) |
| ψ(φ(φ(φ(Ω,0,1),0,0),0,0)) |
ψ(Ω2Ω2×ψ1(Ω2Ω2×ψ1(Ω2Ω2))) |
| ψ(φ(φ(φ(φ(Ω,0,1),0,0),0,0),0,0)) |
ψ(Ω2Ω2×ψ1(Ω2Ω2×ψ1(Ω2Ω2×ψ1(Ω2Ω2)))) |
| ψ(φ(1,0,0,Ω+1)) = ψ(φ(φ(φ(...φ(Ω,0,1)...,0,0),0,0),0,0)) |
ψ(Ω2Ω22) = ψ(Ω2Ω2×Ω2) |
| ψ(φ(1,0,0,0,Ω+1)) |
ψ(Ω2Ω23) |
| ψ(φ(1,0,0,...,Ω+1)) = ψ(φ(1ωΩ+10)) |
ψ(Ω2Ω2ω) |
| ψ(φ(1φ(1φ(1φ(1...)))Ω+10)) = ψ(φ(1ψ(ΩΩΩ)Ω+10)) |
ψ(Ω2Ω2ψ(ΩΩΩ)) |
| ψ(φ(1ψ(φ(1ψ(ΩΩΩ) Ω+10))Ω+10)) |
ψ(Ω2Ω2ψ(Ω2Ω2ψ(ΩΩΩ))) |
| ψ(φ(1Ω10)) = ψ(φ(1ψ(φ(1ψ(φ(1ψ(...) Ω+10))Ω+10))Ω+10)) |
ψ(Ω2Ω2Ω) = ψ(Ω2Ω2ψ(Ω2Ω2ψ(Ω2Ω2...))) |
| ψ(φ(1φ(11Ω+10))) |
ψ(Ω2Ω2ψ1(Ω2))) |
| ψ(φ(1φ(12Ω+10))) |
ψ(Ω2Ω2ψ1(Ω2Ω2))) |
| ψ(φ(1φ(Ω210))) |
ψ(Ω2Ω2ψ1(Ω2Ω2×Ω))) |
| ψ(φ(1φ(1ωΩ+10))) |
ψ(Ω2Ω2ψ1(Ω2Ω2ω))) |
| ψ(φ(1φ(1Ω10))) |
ψ(Ω2Ω2ψ1(Ω2Ω2Ω))) |
| ψ(φ(1φ(1φ(11Ω+10)))) |
ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2)))) |
| ψ(φ(1φ(1φ(12Ω+10)))) |
ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2)))) |
| ψ(φ(1φ(1φ(Ω210)))) |
ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2×Ω)))) |
| ψ(φ(1φ(1φ(1ωΩ+10)))) |
ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2ω)))) |
| ψ(φ(1φ(1φ(1Ω10)))) |
ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2Ω)))) |
| ψ(φ(1φ(1φ(1...φ(1Ω10)...)))) |
ψ(Ω2Ω2Ω2) = ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2ψ1(...))))) |
таб.22 (Сравнение ψ0(n) и ψ0(ψ1(n)))
Таким образом мы снова достигнем бесконечной степенной башни, но уже сделанной из ординалов ω2 (имеющих кардинальность ℵ2). И следуя намеченной нами стратегии, вместо дальнейшего наращивания рекурсий на ω2, мы должны получить их при помощи коллапсирования ординала следующей кардинальности ω3 - минимального ординала с кардинальностью ℵ3. Принципы работы новой коллапсирующей функции будут те же, она будет возвращать ординалы с кардинальностью ℵ2, однако уровень рекурсии заложенный в ней будет намного больше, потому что в качестве аргументов такая функция сможет принимать не только ординалы с кардинальностью ℵ3, но и ординалы с кардинальностью ℵ2, и ординалы с кардинальностью ℵ1, и ординалы с кардинальностью ℵ0 (счетные ординалы), и конечные числа. Полагаю основная идея вам уже понятна, но чтобы еще раз наглядно показать, что с введением каждой дополнительной коллапсирующей функции работающей с бо́льшей кардинальностью, уровень рекурсий будет стремительно расти, я приведу еще одну таблицу, в которой буду сравнивать рекурсивные возможности ψ0(ψ1(n)) и ψ0(ψ1(ψ2(n))). Обратите внимание на одну важную деталь, которая обязательно встретится вам в сравнениях, внутри коллапсирующей функции верхнего уровня не всегда необходимо расколлапсировать ординал до уровня счетного ординала. Так например, ψ(Ω3) = ψ(ψ1(ψ2(Ω3))) - это очень большой рекурсивно-созданный счетный ординал, а ψ1(Ω3) = ψ1(ψ2(Ω3)) - это ψ1(εΩ2+1) - ординал с кардинальностью ℵ1 зарекурсированный до Бахманского уровня. Всю цепочку внутренних коллаппсирующих функций обычно не пишут, ибо она и так подразумевается, поэтому во избежании путаницы при сравнениях эту цепочку приходится достраивать в голове, например, ψ(Ω3+ψ(Ω2)) < ψ(Ω3+ψ1(Ω2)), потому что иначе это выражение можно записать так ψ(Ω3+ψ(ψ1(Ω2))) < ψ(Ω3+ψ1(Ω2)), что так же равносильно выражению ψ(Ω3+ψ(εΩ+1)) < ψ(Ω3+εΩ+1).
| ψ(Ω2) = ψ0(ψ1(Ω2)) |
ψ0(ψ1(ψ2(0))) |
| ψ(Ω2)+1 |
ψ0(ψ1(ψ2(0)))+ψ0(0) |
| ψ(Ω2)×2 |
ψ0(ψ1(ψ2(0)))+ψ0(ψ1(ψ2(0))) |
| ψ(Ω2+1) = ψ(Ω2)×ω |
ψ0(ψ1(ψ2(0))+ψ0(0)) |
| ψ(Ω2+ψ(Ω2)) |
ψ0(ψ1(ψ2(0))+ψ0(ψ1(ψ2(0)))) |
| ψ(Ω2+ψ(Ω2+1)) |
ψ0(ψ1(ψ2(0))+ψ0(ψ1(ψ2(0))+ψ0(0))) |
| ψ(Ω2+ψ(Ω2+ψ(Ω2))) |
ψ0(ψ1(ψ2(0))+ψ0(ψ1(ψ2(0))+ψ0(ψ1(ψ2(0))))) |
| ψ(Ω2+ψ(Ω2+ψ(Ω2+1))) |
ψ0(ψ1(ψ2(0))+ψ0(ψ1(ψ2(0))+ψ0(ψ1(ψ2(0))+ψ0(0)))) |
| ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2)))) |
ψ0(ψ1(ψ2(0))+ψ0(ψ1(ψ2(0))+ψ0(ψ1(ψ2(0))+ψ0(ψ1(ψ2(0)))))) |
| ψ(Ω2+Ω) |
ψ0(ψ1(ψ2(0))+ψ1(0)) |
| ψ(Ω2+Ω2) |
ψ0(ψ1(ψ2(0))+ψ1(ψ1(0))) |
| ψ(Ω2+Ω3) |
ψ0(ψ1(ψ2(0))+ψ1(ψ1(0)+ψ1(0))) |
| ψ(Ω2+ΩΩ) |
ψ0(ψ1(ψ2(0))+ψ1(ψ1(ψ1(0)))) |
| ψ(Ω2+ΩΩΩ) |
ψ0(ψ1(ψ2(0))+ψ1(ψ1(ψ1(ψ1(0))))) |
| ψ(Ω2+ψ1(Ω2)) |
ψ0(ψ1(ψ2(0))+ψ1(ψ2(0))) |
| ψ(Ω2+ψ1(Ω2+1)) |
ψ0(ψ1(ψ2(0))+ψ1(ψ2(0)+ψ0(0))) |
| ψ(Ω2+ψ1(Ω2+ψ(Ω2)) |
ψ0(ψ1(ψ2(0))+ψ1(ψ2(0)+ψ0(ψ1(ψ2(0))))) |
| ψ(Ω2+ψ1(Ω2+Ω)) |
ψ0(ψ1(ψ2(0))+ψ1(ψ2(0)+ψ1(0))) |
| ψ(Ω2+ψ1(Ω2+Ωω)) |
ψ0(ψ1(ψ2(0))+ψ1(ψ2(0)+ψ1(ψ1(1))) |
| ψ(Ω2+ψ1(Ω2+ΩΩ)) |
ψ0(ψ1(ψ2(0))+ψ1(ψ2(0)+ψ1(ψ1(ψ1(0))))) |
| ψ(Ω2+ψ1(Ω2+ψ1(Ω2))) |
ψ0(ψ1(ψ2(0))+ψ1(ψ2(0)+ψ1(ψ2(0)))) |
| ψ(Ω2+ψ1(Ω2+ψ1(Ω2+1))) |
ψ0(ψ1(ψ2(0))+ψ1(ψ2(0)+ψ1(ψ2(0)+ψ0(0)))) |
| ψ(Ω2+ψ1(Ω2+ψ1(Ω2+Ω))) |
ψ0(ψ1(ψ2(0))+ψ1(ψ2(0)+ψ1(ψ2(0)+ψ1(0)))) |
| ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2)))) |
ψ0(ψ1(ψ2(0))+ψ1(ψ2(0)+ψ1(ψ2(0)+ψ1(ψ2(0))))) |
| ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+1)))) |
ψ0(ψ1(ψ2(0))+ψ1(ψ2(0)+ψ1(ψ2(0)+ψ1(ψ2(0)+ψ0(0))))) |
| ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+Ω)))) |
ψ0(ψ1(ψ2(0))+ψ1(ψ2(0)+ψ1(ψ2(0)+ψ1(ψ2(0)+ψ1(0))))) |
| ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2))))) |
ψ0(ψ1(ψ2(0))+ψ1(ψ2(0)+ψ1(ψ2(0)+ψ1(ψ2(0)+ψ1(ψ2(0)))))) |
| ψ(Ω2×2) = ψ(Ω2+Ω2) |
ψ0(ψ1(ψ2(0)+ψ2(0))) = ψ0(ψ1(ψ2(0))+ψ1(ψ2(0)+ψ1(ψ2(0)+...))) |
| ψ(Ω2×3) |
ψ0(ψ1(ψ2(0)+ψ2(0)+ψ2(0))) |
| ψ(Ω2×ω) |
ψ0(ψ1(ψ2(1)) = ψ0(ψ1(ψ2(0)+ψ2(0)+ψ2(0)+...)) |
| ψ(Ω2×Ω) |
ψ0(ψ1(ψ2(ψ1(0)))) |
| ψ(Ω2×Ω2) |
ψ0(ψ1(ψ2(ψ1(ψ1(0))))) |
| ψ(Ω2×ΩΩ) |
ψ0(ψ1(ψ2(ψ1(ψ1(ψ1(0)))))) |
| ψ(Ω2×ψ1(Ω2)) |
ψ0(ψ1(ψ2(ψ1(ψ2(0))))) |
| ψ(Ω2×ψ1(Ω2×ψ1(Ω2))) |
ψ0(ψ1(ψ2(ψ1(ψ2(ψ1(ψ2(0))))))) |
| ψ(Ω22) |
ψ0(ψ1(ψ2(ψ2(0)))) |
| ψ(Ω22×2) |
ψ0(ψ1(ψ2(ψ2(0))+ψ2(ψ2(0)))) |
| ψ(Ω23) |
ψ0(ψ1(ψ2(ψ2(0)+ψ2(0)))) |
| ψ(Ω23×2) |
ψ0(ψ1(ψ2(ψ2(0)+ψ2(0))+ψ2(ψ2(0)+ψ2(0)))) |
| ψ(Ω2ω) |
ψ0(ψ1(ψ2(ψ2(1)))) |
| ψ(Ω2ω×ψ1(Ω2ω)) |
ψ0(ψ1(ψ2(ψ2(1))+ψ1(ψ2(ψ2(1))))) |
| ψ(Ω2ω×ψ1(Ω2ω×ψ1(Ω2ω))) |
ψ0(ψ1(ψ2(ψ2(1))+ψ1(ψ2(ψ2(1))+ψ1(ψ2(ψ2(1))))) |
| ψ(Ω2ω+1) |
ψ0(ψ1(ψ2(ψ2(1)+ψ2(0)))) |
| ψ(Ω2ω2) |
ψ0(ψ1(ψ2(ψ2(2)))) |
| ψ(Ω2ψ(ΩΩ)) |
ψ0(ψ1(ψ2(ψ2(ψ0(ψ1(ψ1(ψ1(0)))))))) |
| ψ(Ω2ψ(Ω2)) |
ψ0(ψ1(ψ2(ψ2(ψ0(ψ1(ψ2(0))))))) |
| ψ(Ω2ψ(Ω2ω)) |
ψ0(ψ1(ψ2(ψ2(ψ0(ψ1(ψ2(ψ2(1)))))))) |
| ψ(Ω2ψ(Ω2ψ(Ω2ω))) |
ψ0(ψ1(ψ2(ψ2(ψ0(ψ1(ψ2(ψ2(ψ0(ψ1(ψ2(ψ2(1)))))))))))) |
| ψ(Ω2ψ(Ω2ψ(Ω2ψ(Ω2ω)))) |
ψ0(ψ1(ψ2(ψ2(ψ0(ψ1(ψ2(ψ2(ψ0(ψ1(ψ2(ψ2(ψ0(ψ1(ψ2(ψ2(1)))))))))))))))) |
| ψ(Ω2Ω) |
ψ0(ψ1(ψ2(ψ2(ψ1(0))))) |
| ψ(Ω2Ω×2) |
ψ0(ψ1(ψ2(ψ2(ψ1(0))))+ψ1(ψ2(ψ2(ψ1(0))))) |
| ψ(Ω2Ω×Ω) |
ψ0(ψ1(ψ2(ψ2(ψ1(0))+ψ1(0)))) |
| ψ(Ω2Ω+1) = ψ(Ω2Ω×Ω2) |
ψ0(ψ1(ψ2(ψ2(ψ1(0)+ψ0(0))))) |
| ψ(Ω2ψ1(Ω2)) = ψ(Ω2εΩ+1) |
ψ0(ψ1(ψ2(ψ2(ψ1(ψ2(0)))))) |
| ψ(Ω2ψ1(Ω2Ω)) |
ψ0(ψ1(ψ2(ψ2(ψ1(ψ2(ψ2(ψ1(0)))))))) |
| ψ(Ω2ψ1(Ω2ψ1(Ω2Ω))) |
ψ0(ψ1(ψ2(ψ2(ψ1(ψ2(ψ2(ψ1(ψ2(ψ2(ψ1(0))))))))))) |
| ψ(Ω2ψ1(Ω2ψ1(Ω2ψ1(Ω2Ω)))) |
ψ0(ψ1(ψ2(ψ2(ψ1(ψ2(ψ2(ψ1(ψ2(ψ2(ψ1(ψ2(ψ2(ψ1(0)))))))))))))) |
| ψ(Ω2Ω2) = ψ(Ω2ψ1(Ω2ψ1(Ω2ψ1(Ω2ψ1(...))))) |
ψ0(ψ1(ψ2(ψ2(ψ2(0))))) |
| ψ(Ω2Ω2×2) |
ψ0(ψ1(ψ2(ψ2(ψ2(0)))+ψ2(ψ2(ψ2(0))))) |
| ψ(Ω2Ω2×ψ(Ω2Ω2)) |
ψ0(ψ1(ψ2(ψ2(ψ2(0))+ψ0(ψ1(ψ2(ψ2(ψ2(0)))))))) |
| ψ(Ω2Ω2×Ω) |
ψ0(ψ1(ψ2(ψ2(ψ2(0))+ψ1(0)))) |
| ψ(Ω2Ω2×ψ1(Ω2)) |
ψ0(ψ1(ψ2(ψ2(ψ2(0))+ψ1(ψ2(0))))) |
| ψ(Ω2Ω2×ψ1(Ω2Ω2)) |
ψ0(ψ1(ψ2(ψ2(ψ2(0))+ψ1(ψ2(ψ2(ψ2(0))))) |
| ψ(Ω2Ω2×Ω2) = ψ(Ω2Ω2+1) |
ψ0(ψ1(ψ2(ψ2(ψ2(0))+ψ2(0)))) |
| ψ(Ω2Ω2+Ω) |
ψ0(ψ1(ψ2(ψ2(ψ2(0))+ψ2(ψ1(0))))) |
| ψ(Ω2Ω2+ψ1(Ω2Ω2)) |
ψ0(ψ1(ψ2(ψ2(ψ2(0))+ψ2(ψ1(ψ2(ψ2(ψ2(0)))))) |
| ψ(Ω2Ω2+ψ1(Ω2Ω2+ψ1(Ω2Ω2))) |
ψ0(ψ1(ψ2(ψ2(ψ2(0))+ψ2(ψ1(ψ2(ψ2(ψ2(0))+ψ2(ψ1(ψ2(ψ2(ψ2(0))))))))) |
| ψ(Ω2Ω2+ψ1(Ω2Ω2+ψ1(Ω2Ω2+ψ1(Ω2Ω2)))) |
ψ0(ψ1(ψ2(ψ2(ψ2(0))+ψ2(ψ1(ψ2(ψ2(ψ2(0))+ψ2(ψ1(ψ2(ψ2(ψ2(0))+
ψ2(ψ1(ψ2(ψ2(ψ2(0)))))))))))) |
| ψ(Ω2Ω2×2) = ψ(Ω2Ω2+Ω2) |
ψ0(ψ1(ψ2(ψ2(ψ2(0))+ψ2(ψ2(0))))) |
| ψ(Ω2Ω2×3) |
ψ0(ψ1(ψ2(ψ2(ψ2(0))+ψ2(ψ2(0))+ψ2(ψ2(0))))) |
| ψ(Ω2Ω2×ω) |
ψ0(ψ1(ψ2(ψ2(ψ2(0)+ψ0(0))))) |
| ψ(Ω2Ω2×ψ(Ω2Ω2)) |
ψ0(ψ1(ψ2(ψ2(ψ2(0)+ψ0(ψ1(ψ2(ψ2(ψ2(0)))))))))) |
| ψ(Ω2Ω2×Ω) |
ψ0(ψ1(ψ2(ψ2(ψ2(0)+ψ1(0))))) |
| ψ(Ω2Ω2×ψ1(Ω2Ω2)) |
ψ0(ψ1(ψ2(ψ2(ψ2(0)+ψ1(ψ2(ψ2(ψ2(0))))))))) |
| ψ(Ω2Ω2×ψ1(Ω2Ω2×ψ1(Ω2Ω2))) |
ψ0(ψ1(ψ2(ψ2(ψ2(0)+ψ1(ψ2(ψ2(ψ2(0)+ψ1(ψ2(ψ2(ψ2(0))))))))))))))) |
| ψ(Ω2Ω2×ψ1(Ω2Ω2×ψ1(Ω2Ω2×ψ1(Ω2Ω2)))) |
ψ0(ψ1(ψ2(ψ2(ψ2(0)+ψ1(ψ2(ψ2(ψ2(0)+ψ1(ψ2(ψ2(ψ2(0)+
ψ1(ψ2(ψ2(ψ2(0)))))))))))))))))) |
| ψ(Ω2Ω22) = ψ(Ω2Ω2×Ω2) |
ψ0(ψ1(ψ2(ψ2(ψ2(0)+ψ2(0))))) |
| ψ(Ω2Ω23) |
ψ0(ψ1(ψ2(ψ2(ψ2(0)+ψ2(0)+ψ2(0))))) |
| ψ(Ω2Ω2ω) |
ψ0(ψ1(ψ2(ψ2(ψ2(1))))) |
| ψ(Ω2Ω2ψ(ΩΩΩ)) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ0(ψ1(ψ1(ψ1(ψ1(0)))))))))) |
| ψ(Ω2Ω2ψ(Ω2Ω2ψ(ΩΩΩ))) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ0(ψ1(ψ2(ψ2(ψ2(ψ0(ψ1(ψ1(ψ1(ψ1(0))))))))))))))) |
| ψ(Ω2Ω2Ω) = ψ(Ω2Ω2ψ(Ω2Ω2ψ(Ω2Ω2...))) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ1(0)))))) |
| ψ(Ω2Ω2ψ1(Ω2))) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(0))))))) |
| ψ(Ω2Ω2ψ1(Ω2Ω2))) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(ψ2(ψ2(0))))))))) |
| ψ(Ω2Ω2ψ1(Ω2Ω2×Ω))) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(ψ2(ψ2(0)+ψ1(0))))))))) |
| ψ(Ω2Ω2ψ1(Ω2Ω2ω))) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(ψ2(ψ2(1))))))))) |
| ψ(Ω2Ω2ψ1(Ω2Ω2Ω))) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(ψ2(ψ2(ψ1(0)))))))))) |
| ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2)))) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(0))))))))))) |
| ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2)))) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(ψ2(ψ2(0))))))))))))) |
| ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2×Ω)))) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(ψ2(ψ2(0)+ψ1(0))))))))))))) |
| ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2ω)))) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(ψ2(ψ2(1))))))))))))) |
| ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2Ω)))) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(ψ2(ψ2(ψ1(ψ2(ψ2(ψ2(ψ1(0)))))))))))))) |
| ψ(Ω2Ω2Ω2) = ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2ψ(...))))) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(0)))))) |
| ψ(Ω2Ω2Ω2+Ω2) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(0))))+ψ2(0))) |
| ψ(Ω2Ω2Ω2×Ω2) = ψ(Ω2Ω2Ω2+1) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(0)))+ψ2(0)))) |
| ψ(Ω2Ω2Ω2+Ω2) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(0)))+ψ2(ψ2(0))))) |
| ψ(Ω2Ω2Ω2+Ω22) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(0)))+ψ2(ψ2(ψ2(0)))))) |
| ψ(Ω2Ω2Ω2×2) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(0)))+ψ2(ψ2(ψ2(ψ2(0))))))) |
| ψ(Ω2Ω2Ω2×ω) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(0))+ψ0(0))))) |
| ψ(Ω2Ω2Ω2×Ω2) = ψ(Ω2Ω2Ω2+1) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(0))+ψ2(0))))) |
| ψ(Ω2Ω2Ω2×2) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(0))+ψ2(ψ2(0)))))) |
| ψ(Ω2Ω2Ω22) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(0)+ψ2(0)))))) |
| ψ(Ω2Ω2Ω2ω) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(1)))))) |
| ψ(Ω2Ω2Ω2Ω) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(ψ1(0))))))) |
| ψ(Ω2Ω2Ω2Ω2) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(ψ2(0))))))) |
| ψ(5Ω2) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(ψ2(ψ2(0)))))))) |
| ψ(6Ω2) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(ψ2(ψ2(ψ2(0))))))))) |
| ψ(7Ω2) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(ψ2(ψ2(ψ2(ψ2(0)))))))))) |
| ψ(8Ω2) |
ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(ψ2(ψ2(ψ2(ψ2(ψ2(0))))))))))) |
| ψ(ωΩ2) = ψ(εΩ2+1) = ψ(φ(1,Ω2+1)) |
ψ(Ω3) = ψ0(ψ1(ψ2(Ω3))) = ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(ψ2(ψ2(ψ2(...))))))))) |
| ψ(εΩ2+1+1) = ψ(εΩ2+1)×ω = ψ(ωεΩ2+1+1) |
ψ(Ω3+1) = ψ(Ω3)×ω |
| ψ(εΩ2+1+ψ(Ω2)) = ψ(εΩ2+1)×ψ(εΩ+1) |
ψ(Ω3+ψ(Ω2)) |
| ψ(εΩ2+1+ψ(εΩ2+1)) = ψ(εΩ2+1)×ψ(εΩ2+1) = ψ(εΩ2+1)2 |
ψ(Ω3+ψ(Ω3)) |
| ψ(εΩ2+1+ψ(εΩ2+1+1)) = ψ(εΩ2+1)ω |
ψ(Ω3+ψ(Ω3+1)) |
| ψ(εΩ2+1+ψ(εΩ2+1+ψ(εΩ2+1))) = ψ(εΩ2+1)ψ(εΩ2+1) |
ψ(Ω3+ψ(Ω3+ψ(Ω3))) |
| ψ(εΩ2+1)ψ(εΩ2+1)ψ(εΩ2+1)... = εψ(εΩ2+1)+1 = φ(1,ψ(εΩ2+1)+1) = ψ(εΩ2+1+Ω) |
ψ(Ω3+Ω) = ψ(Ω3+ψ(Ω3+ψ(Ω3+ψ(Ω3+...)))) |
ψ(εΩ2+1+ΩΩΩΩ...) = ψ(εΩ2+1+εΩ+1) =
ψ(εΩ2+1+ψ1(Ω2)) |
ψ(Ω3+ψ1(Ω2)) |
ψ(εΩ2+1+εΩ+1εΩ+1εΩ+1...) = ψ(εΩ2+1+εΩ+2) =
ψ(εΩ2+1+ψ1(Ω2×2)) |
ψ(Ω3+ψ1(Ω2×2)) |
| ψ(εΩ2+1+ψ1(εΩ2+1)) |
ψ(Ω3+ψ1(Ω3)) |
| ψ(εΩ2+1+ψ1(εΩ2+1+ψ1(εΩ2+1+...))) = ψ(εΩ2+1+Ω2) |
ψ(Ω3+Ω2) = ψ(Ω3+ψ1(Ω3+ψ1(Ω3+ψ1(Ω3+...)))) |
| ψ(εΩ2+1×2) = ψ(εΩ2+1+εΩ2+1) |
ψ(Ω3+ψ2(Ω3)) |
| ψ(εΩ2+1×Ω) = ψ(εΩ2+1×ψ(εΩ2+1×ψ(εΩ2+1×...))) |
ψ(Ω3+ψ2(Ω3+Ω)) |
| ψ(εΩ2+1×Ω2) = ψ(εΩ2+1×ψ1(εΩ2+1×ψ1(εΩ2+1×...))) |
ψ(Ω3+ψ2(Ω3+Ω2)) |
| ψ(εΩ2+1×Ω2Ω2Ω2Ω2...) = ψ(εΩ2+12) = ψ(ωεΩ2+1×2) |
ψ(Ω3+ψ2(Ω3+ψ2(Ω3))) |
| ψ(εΩ2+1ω) = ψ(ωεΩ2+1×ω) = ψ(ωωεΩ2+1+1) |
ψ(Ω3+ψ2(Ω3+ψ2(Ω3+1))) |
| ψ(εΩ2+1ψ(εΩ2+1ψ(εΩ2+1...))) = ψ(εΩ2+1Ω) = ψ(ωωεΩ2+1+Ω) |
ψ(Ω3+ψ2(Ω3+ψ2(Ω3+Ω))) |
| ψ(εΩ2+1ψ1(εΩ2+1ψ1(εΩ2+1...))) = ψ(εΩ2+1Ω2) = ψ(ωωεΩ2+1+Ω2) |
ψ(Ω3+ψ2(Ω3+ψ2(Ω3+Ω2))) |
| ψ(εΩ2+1Ω2Ω2Ω2...) =ψ(εΩ2+1εΩ2+1) = ψ(ωωεΩ2+1×2) |
ψ(Ω3+ψ2(Ω3+ψ2(Ω3+ψ2(Ω3)))) |
| ψ(εΩ2+2) = ψ(εΩ2+1εΩ2+1εΩ2+1...) = ψ(φ(1,Ω2+2)) |
ψ(Ω3×2) = ψ(Ω3+Ω3) = ψ(Ω3+ψ2(Ω3+ψ2(Ω3+ψ2(Ω3)+...))) |
| ψ(εΩ2+Ω) = ψ(εΩ2+ψ(εΩ2+ψ(εΩ2+...))) |
ψ(Ω3×Ω) = ψ(Ω3×ψ(Ω3×ψ(Ω3×ψ(Ω3×...)))) |
| ψ(εΩ2×2) = ψ(εΩ2+Ω2) = ψ(εΩ2+ψ1(εΩ2+ψ1(εΩ2+...))) |
ψ(Ω3×Ω2) = ψ(Ω3×ψ1(Ω3×ψ1(Ω3×ψ1(Ω3×...)))) |
| ψ(εΩ2×Ω) = ψ(εΩ2×ψ(εΩ2×ψ(εΩ2×...))) |
ψ(Ω3×Ω2×Ω) = ψ(Ω3×Ω2×ψ(Ω3×Ω2×ψ(Ω3×Ω2×...))) |
| ψ(εΩ22) = ψ(εΩ2×Ω2) = ψ(εΩ2×ψ1(εΩ2×ψ1(εΩ2×...))) |
ψ(Ω3×Ω22) = ψ(Ω3×Ω2×Ω2) = ψ(Ω3×Ω2×ψ1(Ω3×Ω2×ψ1(Ω3×Ω2×...))) |
| ψ(εΩ2Ω)= ψ(εΩ2ψ(εΩ2ψ(εΩ2...))) |
ψ(Ω3×Ω2Ω) = ψ(Ω3×Ω2ψ(Ω3×Ω2ψ(Ω3×Ω2ψ(...)))) |
| ψ(εΩ2Ω2)= ψ(εΩ2ψ1(εΩ2ψ1(εΩ2...))) |
ψ(Ω3×Ω2Ω2) = ψ(Ω3×Ω2ψ1(Ω3×Ω2ψ1(Ω3×Ω2ψ1(...)))) |
| ψ(εεΩ2+1) = ψ(εΩ2Ω2Ω2Ω2...) |
ψ(Ω3×ψ2(Ω3)) |
| ψ(εεεΩ2+1) = ψ(εεΩ2Ω2Ω2Ω2...) |
ψ(Ω3×ψ2(Ω3×ψ2(Ω3))) |
| ψ(ζΩ2+1) = ψ(φ(2,Ω2+1)) |
ψ(Ω32) = ψ(Ω3×Ω3) = ψ(Ω3×ψ2(Ω3×ψ2(Ω3×ψ2(Ω3×...)))) |
| ψ(ζΩ2+2) = ψ(φ(2,Ω2+2)) |
ψ(Ω32×2) |
| ψ(ηΩ2+1) = ψ(φ(3,Ω2+1)) |
ψ(Ω33) |
| ψ(ηΩ2+2) = ψ(φ(3,Ω2+2)) |
ψ(Ω33×2) |
| ψ(φ(ω,Ω2+1)) |
ψ(Ω3ω) |
| ψ(φ(ψ(φ(ω,Ω2+1)),Ω2+1)) |
ψ(Ω3ψ(Ω3ω)) |
| ψ(φ(ψ(φ(ψ(φ(ω,Ω2+1)),Ω2+1)),Ω2+1)) |
ψ(Ω3ψ(Ω3ψ(Ω3ω))) |
| ψ(φ(Ω,Ω2+1)) = ψ(φ(ψ(φ(ψ(φ(ψ(φ(...,Ω2+1)),Ω2+1)),Ω2+1)),Ω2+1)) |
ψ(Ω3Ω) = ψ(Ω3ψ(Ω3ψ(Ω3...))) |
| ψ(φ(Ω,Ω2+Ω)) = ψ(φ(Ω,ψ(φ(Ω,ψ(φ(Ω,...ψ(φ(Ω,Ω2+1)...))))))) |
ψ(Ω3Ω×Ω) = ψ(Ω3Ω×ψ(Ω3Ω×ψ(Ω3Ω×...))) |
| ψ(φ(Ω,Ω2+Ω2)) = ψ(φ(Ω,ψ1(φ(Ω,ψ1(φ(Ω,...ψ1(φ(Ω,Ω2+1)...))))))) |
ψ(Ω3Ω×Ω2) = ψ(Ω3Ω×ψ1(Ω3Ω×ψ1(Ω3Ω×ψ1(Ω3Ω×...)))) |
| ψ(φ(Ω+1,Ω2+1)) = ψ(φ(Ω,φ(Ω,φ(Ω,φ(Ω,...φ(Ω,Ω2+1)...))))) |
ψ(Ω3Ω+1) = ψ(Ω3Ω×Ω3) = ψ(Ω3Ω×ψ2(Ω3Ω×ψ2(Ω3Ω×ψ2(Ω3Ω×...)))) |
| ψ(φ(εΩ+1,Ω2+1)) = ψ(φ(ψ1(Ω2),Ω2+1)) |
ψ(Ω3ψ1(Ω2)) |
| ψ(φ(ГΩ+1,Ω2+1)) = ψ(φ(ψ1(Ω2Ω2),Ω2+1)) |
ψ(Ω3ψ1(Ω2Ω2)) |
| ψ(φ(ψ1(εΩ2+1),Ω2+1)) = ψ(φ(ψ1(φ(1,Ω2+1)),Ω2+1)) |
ψ(Ω3ψ1(Ω3)) |
| ψ(φ(ψ1(φ(ω,Ω2+1)),Ω2+1)) |
ψ(Ω3ψ1(Ω3ω)) |
| ψ(φ(ψ1(φ(ψ1(φ(ω,Ω2+1)),Ω2+1)),Ω2+1)) |
ψ(Ω3ψ1(Ω3ψ1(Ω3ω))) |
| ψ(φ(Ω2,1)) = ψ(φ(ψ1(φ(ψ1(φ(ψ1(φ(...,Ω2+1)),Ω2+1)),Ω2+1)),Ω2+1)) |
ψ(Ω3Ω2) = ψ(Ω3ψ1(Ω3ψ1(Ω3...))) |
| ψ(φ(Ω2,Ω)) = ψ(φ(Ω2,ψ(φ(Ω2,ψ(φ(Ω2,...)))))) |
ψ(Ω3Ω2×Ω) = ψ(Ω3Ω2×ψ(Ω3Ω2×ψ(Ω3Ω2×...))) |
| ψ(φ(Ω2,Ω2)) = ψ(φ(Ω2,ψ1(φ(Ω2,ψ1(φ(Ω2,...)))))) |
ψ(Ω3Ω2×Ω2) = ψ(Ω3Ω2×ψ1(Ω3Ω2×ψ1(Ω3Ω2×ψ1(Ω3Ω2×...)))) |
| ψ(φ(Ω2+1,0)) = ψ(φ(Ω2,φ(Ω2,φ(Ω2,φ(Ω2,...))))) |
ψ(Ω3Ω2+1) = ψ(Ω3Ω2×Ω3) = ψ(Ω3Ω×ψ2(Ω3Ω2×ψ2(Ω3Ω2×ψ2(Ω3Ω2×...)))) |
| ψ(φ(εΩ2+1,0)) |
ψ(Ω3ψ2(Ω3)) = ψ(Ω2εΩ2+1) |
| ψ(φ(φ(Ω2,1),0)) |
ψ(Ω3ψ2(Ω3Ω2)) |
| ψ(φ(φ(φ(Ω2,1),0),0)) |
ψ(Ω3ψ2(Ω3ψ2(Ω3Ω2))) |
| ψ(φ(φ(φ(φ(Ω2,1),0),0),0)) |
ψ(Ω3ψ2(Ω3ψ2(Ω3ψ2(Ω3Ω2)))) |
| ψ(ГΩ2+1) = ψ(φ(1,0,Ω2+1)) = ψ(φ(φ(φ(...φ(Ω2,1)...,0),0),0)) |
ψ(Ω3Ω3) = ψ(Ω3ψ2(Ω3ψ2(Ω3ψ2(Ω3ψ2(...))))) |
| ψ(φ(1,0,0,Ω2+1)) = ψ(φ(φ(φ(...φ(Ω2,0,1)...,0,0),0,0),0,0)) |
ψ(Ω3Ω32) = ψ(Ω3Ω3×Ω3) |
| ψ(φ(1,0,0,...,Ω2+1)) = ψ(φ(1ωΩ2+10)) |
ψ(Ω2Ω2ω) |
| ψ(φ(1ΩΩ2+10)) = ψ(φ(1ψ(φ(1ψ(φ(1ψ(...) Ω2+10))Ω2+10))Ω2+10)) |
ψ(Ω3Ω3Ω) = ψ(Ω3Ω3ψ(Ω3Ω3ψ(Ω3Ω3...))) |
| ψ(φ(1Ω210)) = ψ(φ(1ψ1(φ(1ψ1(φ(1ψ1(...) Ω2+10))Ω2+10))Ω2+10)) |
ψ(Ω3Ω3Ω2) = ψ(Ω3Ω3ψ1(Ω3Ω3ψ1(Ω3Ω3...))) |
| ψ(φ(1φ(1Ω210))) |
ψ(Ω3Ω3ψ2(Ω3Ω3Ω2))) |
| ψ(φ(1φ(1φ(1Ω210)))) |
ψ(Ω3Ω3ψ2(Ω3Ω3ψ2(Ω3Ω3Ω2)))) |
| ψ(φ(1φ(1φ(1...φ(1Ω210)...)))) |
ψ(Ω3Ω3Ω3) = ψ(Ω3Ω3ψ2(Ω3Ω3ψ2(Ω3Ω3ψ2(...))))) |
таб.23 (Сравнение ψ0(ψ1(n)) и ψ0(ψ1(ψ2(n))))
В сухом остатке от всех этих сравнений мы можем вывести единые принципы сравнения коллапсирующих функций высших уровней с коллапсирующими функциями низших уровней.
ε0 = φ(1,0) = ψ(Ω) = ψ0(ψ1(0))
ζ0 = φ(2,0) = ψ(Ω2) = ψ0(ψ1(ψ1(0)))
Г0 = φ(1,0,0) = ψ(ΩΩ) = ψ0(ψ1(ψ1(ψ1(0))))
φ(1φ(1φ(1φ(1...)))) = ψ(ΩΩΩ) = ψ0(ψ1(ψ1(ψ1(ψ1(0)))))
ψ(ΩΩΩΩ) = ψ0(ψ1(ψ1(ψ1(ψ1(ψ1(0))))))
ψ(εΩ+1) = ψ(Ω2) = ψ0(ψ1(ψ2(0)))
ψ(ζΩ+1) = ψ(Ω22) = ψ0(ψ1(ψ2(ψ2(0))))
ψ(ГΩ+1) = ψ(Ω2Ω2) = ψ0(ψ1(ψ2(ψ2(ψ2(0)))))
ψ(φ(1φ(1φ(1...φ(1Ω10)...)))) = ψ(Ω2Ω2Ω2) = ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(0))))))
ψ(Ω2Ω2Ω2Ω2) = ψ0(ψ1(ψ2(ψ2(ψ2(ψ2(ψ2(0)))))))
ψ(εΩ2+1) = ψ(Ω3) = ψ0(ψ1(ψ2(ψ3(0))))
ψ(ζΩ2+1) = φ(1,Ω2+1) = ψ(Ω32) = ψ0(ψ1(ψ2(ψ3(ψ3(0)))))
ψ(ГΩ2+1) = φ(1,0,Ω2+1) = ψ(Ω3Ω3) = ψ0(ψ1(ψ2(ψ3(ψ3(ψ3(0))))))
ψ(φ(1φ(1φ(1...φ(1Ω210)...)))) = ψ(Ω3Ω3Ω3) = ψ0(ψ1(ψ2(ψ3(ψ3(ψ3(ψ3(0)))))))
ψ(Ω3Ω3Ω3Ω3) = ψ0(ψ1(ψ2(ψ3(ψ3(ψ3(ψ3(ψ3(0)))))))
ψ(εΩ3+1) = ψ(Ω4) = ψ0(ψ1(ψ2(ψ3(ψ4(0)))))
ψ(Ωn) = ψ0(ψ1(ψ2(ψ3(ψ4(...ψn(0)...)))))
ψ(Ωn2) = ψ0(ψ1(ψ2(ψ3(ψ4(...ψn(ψn(0))...)))))
ψ(ΩnΩn) = ψ0(ψ1(ψ2(ψ3(ψ4(...ψn(ψn(ψn(0)))...)))))
ψ(ΩnΩnΩn) = ψ0(ψ1(ψ2(ψ3(ψ4(...ψn(ψn(ψn(ψn(0))))...)))))
ψ(ΩnΩnΩnΩn) = ψ0(ψ1(ψ2(ψ3(ψ4(...ψn(ψn(ψn(ψn(ψn(0)))))...)))))
ψ(εΩn+1) = ψ(Ωn+1) = ψ0(ψ1(ψ2(ψ3(ψ4(...ψn(ψn+1(0))...)))))
В конечном итоге, следуя этой схеме введения коллапсирующих функций внутрь других коллапсирующих функций, мы получим вот такой ординал: ψ(Ωω) = ψ(sup(Ωn)|n<ω) = ψ0(ψ1(ψ2(ψ3(ψ4(ψ5(ψ6(...))))))). Данный ординал носит свое название в честь создателя коллапсирующей функции, которой мы пользуемся, Ординал Бухольца (Buchholz ordinal). Коллапсирующая функция, которую определил Бухольц, превосходит коллапсирующую функцию Бахмана, за счет того, что в своем определении она уже содержит в себе все дополнительные высшие коллапсирующие функции, это и позволяет добраться до таких масштабов. Но на самом деле функция Бухольца, способна на бо́льшее и об этом мы еще поговорим, а пока давайте осмотримся на тех масштабах, которых мы достигли.
Тот предел, которого мы достигли, соответствует рекурсивным возможностям подсистем П11-CA0, Σ11-CA0 и Δ12-CA0 арифметики второго порядка, то есть ψ(Ωω) является PTO для данных теорий. Наша схема получения очень большого числа по методу следующей цепочки: конечное число ← фундаментальная последовательность ← FGH|счетный ординал|=ℵ0 ← коллапсирование ← OCF0(|несчетный ординал|=ℵ1) ← коллапсирование ← OCF1(|несчетный ординал|=ℵ2) ← коллапсирование ← OCF2(|несчетный ординал|=ℵ3) ← ... ← коллапсирование ← OCFn-1(|несчетный ординал|=ℵn), причем совершенно неважно какую быстрорастущую иерархию (FGH) и ординальную коллапсирующую функцию (OCF) мы используем - такая конструкция максимум, что можно выжать из любой потенциально-возможной рекурсивной формулы заданной на множествах натуральных чисел и содержащей только один вид неограниченного квантора "∀" (для каждого) - в случае с подсистемой П11-CA0, или "∃" (существует) - в случае с подсистемой Σ11-CA0. Так же это будет пределом и для любой рекурсивной формулы заданной на множестве натуральных чисел и содержащей оба вида кванторов, но с однократным чередованием (например, содержащей любое количество "∀" и любое количество следующих за ними "∃"), при условии что она будет эквивалентна некой другой формуле с обратным однократным чередованием видов кванторов (например, содержащей любое количество "∃" и любое количество следующих за ними "∀"). Такие рекурсивные формулы это предел возможностей подсистемы Δ12-CA0. Хочу отметить важную деталь, что во всех этих подсистемах, аксиома индукции должна быть применима только к натуральным числам, то есть должна звучать как в арифметике первого порядка, иначе подсистемы будут сильнее (такие модификации подсистем П11, Σ11 и Δ12 мы разберем далее).
Следующее расширение массивной нотации тоже построено на функции, которая является разновидностью вышеупомянутых формул. Значит и ее предел тоже определяется Ординалом Бухольца ψ(Ωω). Как вы можете вспомнить предыдущее расширение называлось Первично расширяющейся массивной нотацией, в которой вводился так называемый разделитель первичного расширения и связанный с ним процесс расширения массива. Думаю многие догадались, что раз существует разделитель первичного расширения, значит должен существовать и разделитель вторичного, троичного и так далее, n-ичного расширения. Функцию совсем не сложно модифицировать так чтобы ввести в нее все эти разделители, тогда процесс расширения массива задействует все возможности П11-формулы. Давайте продемонстрирую как будет работать множественное расширение. Для начала выразим выведенные нами ранее разделители первичного расширения разных уровней с использованием разделителя вторичного расширения:
' = (1') = (1''1')
(2') = (2''1')
(1,2') = (1,2''1')
(1'2') = (1(1''1')2''1')
(1(2')2') = (1(2''1')2''1')
(1(1'2')2') = (1(1(1''1')2''1')2''1')
(1(1(2')2')2') = (1(1(2''1')2''1')2''1')
(1(1(1'2')2')2') = (1(1(1(1''1')2''1')2''1')2''1')
(1(1(1(2')2')2')2') = (1(1(1(2''1')2''1')2''1')2''1')
(1(1(1(1'2')2')2')2') = (1(1(1(1(1''1')2''1')2''1')2''1')2''1')
И начиная с разделителя (1''2'), вторичное расширение уже будет создавать систему вложенных разделителей первичного расширения, по следующему методу: {n,m(1(1''2')2)2} = {n,n(1(1(1(1(1(...(1'2')...)2')2')2')2')2)2} - где m-1 вложений и это по скорости роста соответствует ординалу Бахмана-Говарда ψ(εΩ+1) = ψ(Ω2). Вы так же должны помнить, что после достижения некого рекурсивного предела, чтобы относительно него хоть немного существенно сдвинуться дальше, необходимо пройти такой же круг рекурсий и тогда выражение: {n,m,2(1(1''2')2)2} = {n,n(1(1(1(1(1(...(1'2')...)2')2')2')2')2)2} - где {n,n(1(1(1(1(1(...(1'2')...)2')2')2')2')2)2} - где ... и так m+2 раз - практически совсем не продвинет нас до ординала ψ(Ω2)+1. Для достижения данного уровня, необходимо так же как и в случае перехода от просто расширенных массивов к первично расширяющимся массивам, пройти следующие рекурсии: {n,m(1(1''2')2)3} = {n,n(1(1(1(1(1(...(1'2')...)2')2')2')2')2)2(1(1''2')2)2} - где m-1 вложений, затем {n,m(1(1''2')2)1(1(1''2')2)2} = {n,m(1(1''2')2)1(1(1(1(1(1(...(1'2')...)2')2')2')2')2)2} - где m-1 вложений, и наконец {n,m(2(1''2')2)2} = {n,m(1(1''2')2)1(1(1''2')2)1(1(1''2')2)...2} где m+2 вхождений разделителя (1(1''2')2). И только тогда мы получим скорость роста соотвествующую быстрорастущей иерархии с ординалом ψ(Ω2)+1. Дальше процесс рекурсирования идет аналогично первичному расширению, и подробно его разибрать я не буду, намного больше вам расскажут сравнения приведенные ниже. И как только мы доберемся до выражения: {n,n(1(1(1'''2'')2')2)2} = {n,n(1(1(1(1(1(...(1"2'')...)2'')2'')2'')2')2)2} - где m-1 вложений, можно призывать на помощь разделитель третичного расширения, с помощью которого так же можно выразить вторичное расширение по следующей схеме:
'' = (1'') = (1'''1'')
(2'') = (2'''1'')
(1,2'') = (1,2'''1'')
(1''2'') = (1(1'''1'')2'''1'')
(1(2'')2'') = (1(2'''1'')2'''1'')
(1(1''2'')2'') = (1(1(1'''1'')2'''1'')2'''1'')
(1(1(2'')2'')2'') = (1(1(2'''1'')2'''1'')2'''1'')
(1(1(1''2'')2'')2'') = (1(1(1(1'''1'')2'''1'')2'''1'')2'''1'')
(1(1(1(2'')2'')2'')2'') = (1(1(1(2'''1'')2'''1'')2'''1'')2'''1'')
(1(1(1(1''2'')2'')2'')2'') = (1(1(1(1(1'''1'')2'''1'')2'''1'')2'''1'')2'''1'')
И так же, начиная с разделителя (1'''2''), третичное расширение будет расширяться, формируя систему вложенных уровней вторичного расширения. Аналогично, четвертичное расширение, начиная с разделителя (1''''2'''), будет расширяться, формируя систему вложенных уровней третичного расширения. И так далее, пока мы не дотигнем n-ичног расширения, которое будет по скорости роста соотвествовать быстрорастущей иерархии с ординалом Бухольца ψ(Ωω). Как не трудно будет заметить в сравнениях n-ичность расширения будет соотвествовать n-ному уровню коллапсирующей функции для получения счетного ординала соотвествующему данной скорости роста. В целом понять масштабы этого расширения массивной нотации можно интуитивно, но тем не менее я должен привести формальное определение правил вычисления нотации и список сравнений с рекурсивным потенциалом ординалов. Предлагаю вам со всем этим ознакомиться ниже.
Множественно расширяющаяся массивная нотация (Multiple expanding array notation)
Определение:
Действительны все определения Primary expanding array notation
“ '' ” - двойной апостроф - разделитель вторичного расширения, является краткой записью (1'')
Следовательно (2'') - разделитель вторичного расширения следующего порядка.
“ ''' ” - тройной апостроф - разделитель третичного расширения, является краткой записью (1''')
Следовательно (2''') - разделитель третичного расширения следующего порядка.
“ ''...' ” - n-ной апостроф - разделитель n-ного расширения, является краткой записью (1'n)
Правила:
Правило 1: (Правило базы - если в массиве два вхождения) {a,b} = ab
Правило 2: (Правило хвоста - если последнее вхождение массива или разделителя равно 1) {# S 1} = {#} или (# S 1) = (#)
Правило 3: (Правило рекурсии - если 2-е и 3-е вхождение не равно 1) {a,b,c #} = {a,{a,b-1,c #},c-1 #}
Правило 4: (Правило свертывания - если lv(S) < lv(S+), для массива или разделителя) {# S 1 S+ #+} = {# B #+} или (# S 1 S+ #+) = (# B #+)
“#” и “#+” - какие-то строки вхождений и разделителей, также могут быть пустыми.
“S” и “S+” - разделители.
Процесс:
Циклично и последовательно проверяем выполнение 4-х приведенных выше правил, пока не выполнится первое правило.
Если ни одно из 4-х приведенных выше правил не применяется, то запускается процесс исключений.
Начинаем с 3-ого вхождения:
Случай A: Если вхождение равно 1, тогда переходим к следующему вхождению.
Случай B: Если вхождение не равно 1, тогда смотрим на предыдущий элемент:
Случай B1: Если это запятая “,” тогда:
1) изменяем “1,n” (это вхождение и предыдущую единицу) на “b,n-1”, где b - итератор.
2) изменяем все предыдущие вхождения в базовом слое на a, где a - база.
3) закончить и перейти к проверке правил.
Случай B2: Если это M = “ ''...' ” - m-ной апостроф, тогда:
1) пусть t это слой, на котором находится M.
2) повторяем:
а. вычесть 1 из t.
b. пусть разделитель Bt находится в слое t и в нем находится M.
с. если t = 1, то переходим к следующему пункту иначе повторяем этот пункт.
3) находим максимальный t, такой, чтобы разделитель At имел ровно m-1 апострофов “ ''...' ” вверху сразу перед закрывающейся скобкой “)”.
4) пусть строки P и Q будут такими, что Bt = “P M n Q”
5) изменяем Bt на Sb, где b - итератор, S1 - “,” - запятая, и Si+1 = “P 1 Si 2 M n-1 Q”
6) закончить и перейти к проверке правил.
Случай B3: Если это разделитель K, не являющийся запятой или апострофом, тогда
1) изменяем “K n” на “K 2 K n-1”.
2) установите разделитель At = K, теперь K находится на слое t.
3) переходим к первому вхождению в первом из K.
Случай B4: Если это открывающаяся скобка “(” тогда:
1) изменяем разделитель “(n #)” на строку Sb, где b это итератор, S1 = “(n-1 #)” и Si+1 = “Si 1 (n-1 #)”.
2) закончить и перейти к проверке правил.
Первоначальное авторство: Крис Бёрд, 2014 год.
Последующая модификация: Hypcos, 2015 год.
приложение 18 (Множественно расширяющаяся массивная нотация)
ψ(Ω2) = ψ(εΩ+1) = ψ(ωΩ) ~~ {n,n(1(1''2')2)2}
ψ(Ω2)+1 ~~ {n,n(2(1''2')2)2}
ψ(Ω2)×2 ~~ {n,n(1(1(1''2')2)2(1''2')2)2}
ψ(Ω2+1) = ψ(Ω2)×ω ~~ {n,n(1(1(1''2')2)1,2(1''2')2)2}
ψ(Ω2+ψ(Ω)) ~~ {n,n(1(1(1''2')2)1(1'2)2)2(1''2')2)2}
ψ(Ω2+ψ(Ω2)) ~~ {n,n(1(1(1''2')2)1(1(1''2')2)2(1''2')2)2}
ψ(Ω2+ψ(Ω2+1)) ~~ {n,n(1(2(1''2')2)2(1''2')2)2}
ψ(Ω2+ψ(Ω2+ψ(Ω2))) ~~ {n,n(1(1(1''2')2)2(1''2')2)2(1''2')2)2}
ψ(Ω2+ψ(Ω2+ψ(Ω2+1))) ~~ {n,n(1(1(1(1''2')2)1,2(1''2')2)2(1''2')2)2}
ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2)))) ~~ {n,n(1(1(1(1''2')2)1(1(1''2')2)2(1''2')2)2(1''2')2)2}
ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+1)))) ~~ {n,n(1(1(2(1''2')2)2(1''2')2)2(1''2')2)2}
ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2))))) ~~ {n,n(1(1(1(1''2')2)2(1''2')2)2(1''2')2)2(1''2')2)2}
ψ(Ω2+Ω) = εψ(Ω2)+1 ~~ {n,n(1'2(1''2')2)2}
ψ(Ω2+Ω2) ~~ {n,n(1'1'2(1''2')2)2}
ψ(Ω2+Ω3) ~~ {n,n(1'1'1'2(1''2')2)2}
ψ(Ω2+Ωω) ~~ {n,n(1(2')2(1''2')2)2}
ψ(Ω2+ΩΩ) ~~ {n,n(1(1'2')2(1''2')2)2}
ψ(Ω2+ΩΩΩ) ~~ {n,n(1(1'1'2')2(1''2')2)2}
ψ(Ω2+ΩΩΩΩ) ~~ {n,n(1(1(1'2')2')2(1''2')2)2}
ψ(Ω2+ψ1(Ω2)) = ψ(Ω2+εΩ+1) ~~ {n,n(1(1''2')3)2}
ψ(Ω2+ψ1(Ω2+1)) ~~ {n,n(1(1''2')1,2)2}
ψ(Ω2+ψ1(Ω2+ψ(Ω2)) ~~ {n,n(1(1''2')1(1(1''2')2)2)2}
ψ(Ω2+ψ1(Ω2+Ω)) ~~ {n,n(1(1''2')1'2)2}
ψ(Ω2+ψ1(Ω2+Ωω)) ~~ {n,n(1(1''2')1(2')2)2}
ψ(Ω2+ψ1(Ω2+ΩΩ)) ~~ {n,n(1(1''2')1(1'2')2)2}
ψ(Ω2+ψ1(Ω2+ψ1(Ω2))) ~~ {n,n(1(1''2')1(1''2')2)2}
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+1))) ~~ {n,n(1(2''2')2)2}
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+Ω))) ~~ {n,n(1(1'2''2')2)2}
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2)))) ~~ {n,n(1(1(1''2')2''2')2)2}
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+1)))) ~~ {n,n(1(1(1''2')1,2''2')2)2}
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+Ω)))) ~~ {n,n(1(1(1''2')1'2''2')2)2}
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2))))) ~~ {n,n(1(1(1''2')1(1''2')2''2')2)2}
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+1))))) ~~ {n,n(1(1(2''2')2''2')2)2}
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2)))))) ~~ {n,n(1(1(1(1''2')2''2')2''2')2)2}
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2+ψ1(Ω2)))))))) ~~ {n,n(1(1(1(1''2')1(1''2')2''2')2''2')2)2}
ψ(Ω2×2) = ψ(Ω2+Ω2) = ψ(εΩ+2) ~~ {n,n(1(1''3')2)2}
ψ(Ω2×3) ~~ {n,n(1(1''4')2)2}
ψ(Ω2×ω) ~~ {n,n(1(1''1,2')2)2}
ψ(Ω2×Ω) ~~ {n,n(1(1''1'2')2)2}
ψ(Ω2×Ω2) ~~ {n,n(1(1''1'1'2')2)2}
ψ(Ω2×ΩΩ) ~~ {n,n(1(1''1(1'2')2')2)2}
ψ(Ω2×ψ1(Ω2)) ~~ {n,n(1(1''1(1''2')2')2)2}
ψ(Ω2×ψ1(Ω2+1)) ~~ {n,n(1(1''1(1''2')1,2')2)2}
ψ(Ω2×ψ1(Ω2×2)) ~~ {n,n(1(1''1(1''3')2')2)2}
ψ(Ω2×ψ1(Ω2×ω)) ~~ {n,n(1(1''1(1''1,2')2')2)2}
ψ(Ω2×ψ1(Ω2×ψ1(Ω2))) ~~ {n,n(1(1''1(1''1(1''2')2')2')2)2}
ψ(Ω22) = ψ(Ω2×Ω2) = ψ(ζΩ+1) ~~ {n,n(1(1''1''2')2)2} = {n,n(1(1''1(1''1(1''...2')2')2')2')2)2} - где n-вложений
ψ(Ω22+1) ~~ {n,n(2(1''1''2')2)2}
ψ(Ω22+ψ(Ω)) ~~ {n,n(1(1'2)2(1''1''2')2)2}
ψ(Ω22+ψ(Ω2)) ~~ {n,n(1(1(1''2')2)2(1''1''2')2)2}
ψ(Ω22+ψ(Ω22)) ~~ {n,n(1(1(1''1''2')2)2(1''1''2')2)2}
ψ(Ω22+Ω) ~~ {n,n(1'2(1''1''2')2)2}
ψ(Ω22+ψ1(Ω22)) ~~ {n,n(1(1''1''2')3)2}
ψ(Ω22+ψ1(Ω22+1)) ~~ {n,n(1(1''1''2')1,2)2}
ψ(Ω22+ψ1(Ω22+ψ1(Ω22))) ~~ {n,n(1(1''1''2')1(1''1''2')2)2}
ψ(Ω22+ψ1(Ω22+ψ1(Ω22+1))) ~~ {n,n(1(2''1''2')2)2}
ψ(Ω22+ψ1(Ω22+ψ1(Ω22+ψ1(Ω22)))) ~~ {n,n(1(1(1''1''2')2''1''2')2)2}
ψ(Ω22+Ω2) ~~ {n,n(1(1''2''2')2)2}
ψ(Ω22+Ω2×2) ~~ {n,n(1(1''3''2')2)2}
ψ(Ω22+Ω2×ω) ~~ {n,n(1(1''1,2''2')2)2}
ψ(Ω22+Ω2×ψ(Ω22)) ~~ {n,n(1(1''1(1(1''1''2')2)2''2')2)2}
ψ(Ω22+Ω2×Ω) ~~ {n,n(1(1''1'2''2')2)2}
ψ(Ω22+Ω2×ψ1(Ω22)) ~~ {n,n(1(1''1(1''1''2')2''2')2)2}
ψ(Ω22+Ω2×ψ1(Ω22+Ω2×ψ1(Ω22))) ~~ {n,n(1(1''1(1''1(1''1''2')2''2')2''2')2)2}
ψ(Ω22×2) = ψ(Ω22×Ω22) = ψ(ζΩ+2) ~~ {n,n(1(1''1''3')2)2} = {n,n(1(1''1(1''1(1''...''2')2''2')2''2')2''2')2)2} - где n-вложений
ψ(Ω22×3) ~~ {n,n(1(1''1''4')2)2}
ψ(Ω22×ω) ~~ {n,n(1(1''1''1,2')2)2}
ψ(Ω22×ψ(Ω22)) ~~ {n,n(1(1''1''1(1(1''1''2')2)2')2)2}
ψ(Ω22×Ω) ~~ {n,n(1(1''1''1'2')2)2}
ψ(Ω22×ψ1(Ω22)) ~~ {n,n(1(1''1''1(1''1''2')2')2)2}
ψ(Ω22×ψ1(Ω22×ψ1(Ω22))) ~~ {n,n(1(1''1''1(1''1''1(1''1''2')2')2')2)2}
ψ(Ω23) = ψ(Ω22×Ω2) = ψ(ηΩ+1) ~~ {n,n(1(1''1''1''2')2)2} = {n,n(1(1''1''1(1''1''1(1''1''...2')2')2')2')2)2} - где n-вложений
ψ(Ω23×2) = ψ(ηΩ+2) ~~ {n,n(1(1''1''1''3')2)2}
ψ(Ω2ω) ~~ {n,n(1(1(2'')2')2)2} = {n,n(1(1''1''1''1''1''...n-раз...''2')2)2}
ψ(Ω2ω+1) ~~ {n,n(2(1(2'')2')2)2}
ψ(Ω2ω+ψ(Ω)) ~~ {n,n(1(1'2)2(1(2'')2')2)2}
ψ(Ω2ω+ψ(Ω2)) ~~{n,n(1(1(1''2')2)2(1(2'')2')2)2}
ψ(Ω2ω+Ω) ~~ {n,n(1'2(1(2'')2')2)2}
ψ(Ω2ω+Ω2) ~~ {n,n(1'1'2(1(2'')2')2)2}
ψ(Ω2ω+Ωω) ~~ {n,n(1(2')2(1(2'')2')2)2}
ψ(Ω2ω+ψ1(Ω2)) ~~ {n,n(1(1''2')2(1(2'')2')2)2}
ψ(Ω2ω+ψ1(Ω22)) ~~ {n,n(1(1''1''2')2(1(2'')2')2)2}
ψ(Ω2ω+ψ1(Ω23)) ~~ {n,n(1(1''1''1''2')2(1(2'')2')2)2}
ψ(Ω2ω+ψ1(Ω2ω)) ~~ {n,n(1(1(2'')2')3)2}
ψ(Ω2ω+ψ1(Ω2ω+1)) ~~ {n,n(1(1(2'')2')1,2)2}
ψ(Ω2ω+ψ1(Ω2ω+ψ1(Ω2ω))) ~~ {n,n(1(1(2'')2')1(1(2'')2')2)2}
ψ(Ω2ω+ψ1(Ω2ω+ψ1(Ω2ω+1))) ~~ {n,n(1(2(2'')2')2)2}
ψ(Ω2ω+ψ1(Ω2ω+ψ1(Ω2ω+ψ1(Ω2ω)))) ~~ {n,n(1(1(1(2'')2')2(2'')2')2)2}
ψ(Ω2ω+Ω2) ~~ {n,n(1(1''2(2'')2')2)2}
ψ(Ω2ω+Ω2×2) ~~ {n,n(1(1''3(2'')2')2)2}
ψ(Ω2ω+Ω2×ω) ~~ {n,n(1(1''1,2(2'')2')2)2}
ψ(Ω2ω+Ω2×ψ(Ω2)) ~~ {n,n(1(1''1(1(1''2')2)2(2'')2')2)2}
ψ(Ω2ω+Ω2×Ω) ~~ {n,n(1(1''1'2(2'')2')2)2}
ψ(Ω2ω+Ω22) ~~ {n,n(1(1''1''2(2'')2')2)2}
ψ(Ω2ω+Ω23) ~~ {n,n(1(1''1''1''2(2'')2')2)2}
ψ(Ω2ω×2) ~~ {n,n(1(1(2'')3')2)2}
ψ(Ω2ω×ω) ~~ {n,n(1(1(2'')1,2')2)2}
ψ(Ω2ω×ψ(Ω)) ~~ {n,n(1(1(2'')1(1'2)2')2)2}
ψ(Ω2ω×Ω) ~~ {n,n(1(1(2'')1'2')2)2}
ψ(Ω2ω×ψ1(Ω2)) ~~ {n,n(1(1(2'')1(1''2')2')2)2}
ψ(Ω2ω×ψ1(Ω2ω)) ~~ {n,n(1(1(2'')1(1(2'')2')2')2)2}
ψ(Ω2ω×ψ1(Ω2ω×ψ1(Ω2ω))) ~~ {n,n(1(1(2'')1(1(2'')1(1(2'')2')2')2')2)2}
ψ(Ω2ω+1) ~~ {n,n(1(1(2'')1''2')2)2}
ψ(Ω2ω+2) ~~ {n,n(1(1(2'')1''1''2')2)2}
ψ(Ω2ω×2) ~~ {n,n(1(1(2'')1(2'')2')2)2}
ψ(Ω2ω2) ~~ {n,n(1(1(3'')2')2)2}
ψ(Ω2ωω) ~~ {n,n(1(1(1,2'')2')2)2}
ψ(Ω2ψ(ΩΩ)) ~~ {n,n(1(1(1(1(1'2')2)2'')2')2)2}
ψ(Ω2ψ(Ω2)) ~~ {n,n(1(1(1(1(1''2')2)2'')2')2)2}
ψ(Ω2ψ(Ω2ω)) ~~ {n,n(1(1(1(1(1(2'')2')2)2'')2')2)2}
ψ(Ω2ψ(Ω2ψ(Ω2ω))) ~~ {n,n(1(1(1(1(1(1(1(1(2'')2')2)2'')2')2)2'')2')2)2}
ψ(Ω2ψ(Ω2ψ(Ω2ψ(Ω2ω)))) ~~ {n,n(1(1(1(1(1(1(1(1(1(1(1(2'')2')2)2'')2')2)2'')2')2)2'')2')2)2}
ψ(Ω2Ω) ~~ {n,n(1(1(1'2'')2')2)2} = {n,n(1(1(1(1(1(1(1(1(1...2'')2')2)2'')2')2)2'')2')2)2} - где n-вложений
ψ(Ω2Ω×2) ~~ {n,n(1(1(1'2'')3')2)2}
ψ(Ω2Ω×Ω) ~~ {n,n(1(1(1'2'')1'2')2)2}
ψ(Ω2Ω+1) = ψ(Ω2Ω×Ω2) ~~ {n,n(1(1(1'2'')1''2')2)2}
ψ(Ω2Ω+2) ~~ {n,n(1(1(1'2'')1''1''2')2)2}
ψ(Ω2Ω+ω) ~~ {n,n(1(1(1'2'')1(2'')2')2)2}
ψ(Ω2Ω×2) ~~ {n,n(1(1(1'2'')1(1'2'')2')2)2}
ψ(Ω2Ω×ω) ~~ {n,n(1(1(2'2'')2')2)2}
ψ(Ω2Ω2) ~~ {n,n(1(1(1'3'')2')2)2}
ψ(Ω2Ωω) ~~ {n,n(1(1(1'1,2'')2')2)2}
ψ(Ω2ΩΩ) ~~ {n,n(1(1(1'1'2'')2')2)2}
ψ(Ω2ΩΩΩ) ~~ {n,n(1(1(1(1'2')2'')2')2)2}
ψ(Ω2ψ1(Ω2)) = ψ(Ω2εΩ+1) ~~ {n,n(1(1(1(1''2')2'')2')2)2}
ψ(Ω2ψ1(Ω2Ω)) ~~ {n,n(1(1(1(1(1'2'')2')2'')2')2)2}
ψ(Ω2ψ1(Ω2ψ1(Ω2))) ~~ {n,n(1(1(1(1(1(1''2')2'')2')2'')2')2)2}
ψ(Ω2ψ1(Ω2ψ1(Ω2Ω))) ~~ {n,n(1(1(1(1(1(1(1'2'')2')2'')2')2'')2')2)2}
ψ(Ω2ψ1(Ω2ψ1(Ω2ψ1(Ω2)))) ~~ {n,n(1(1(1(1(1(1(1''2'')2')2'')2')2'')2')2)2}
ψ(Ω2ψ1(Ω2ψ1(Ω2ψ1(Ω2Ω)))) ~~ {n,n(1(1(1(1(1(1(1(1(1'2'')2')2'')2')2'')2')2'')2')2)2}
ψ(Ω2Ω2) ~~ {n,n(1(1(1''2'')2')2)2} = {n,n(1(1(1(1(1(1(1(1(1...2'')2')2'')2')2'')2')2'')2')2)2} - где n-вложений
ψ(Ω2Ω2×2) ~~ {n,n(1(1(1''2'')3')2)2}
ψ(Ω2Ω2×ψ(Ω2Ω2)) ~~ {n,n(1(1(1''2'')1(1(1(1''2'')2')2)2')2)2}
ψ(Ω2Ω2×Ω) ~~ {n,n(1(1(1''2'')1'2')2)2}
ψ(Ω2Ω2×ψ1(Ω2)) ~~ {n,n(1(1(1''2'')1(1''2')2')2)2}
ψ(Ω2Ω2×ψ1(Ω2Ω2)) ~~ {n,n(1(1(1''2'')1(1(1''2'')2')2')2)2}
ψ(Ω2Ω2×Ω2) = ψ(Ω2Ω2+1) ~~ {n,n(1(1(1''2'')1''2')2)2}
ψ(Ω2Ω2+Ω) ~~ {n,n(1(1(1''2'')1(1'2'')2')2)2}
ψ(Ω2Ω2+ψ1(Ω2Ω2)) ~~ {n,n(1(1(1''2'')1(1(1(1''2'')2')2'')2')2)2}
ψ(Ω2Ω2+ψ1(Ω2Ω2+ψ1(Ω2Ω2))) ~~ {n,n(1(1(1''2'')1(1(1(1(1(1''2'')2')2'')2')2'')2')2)2}
ψ(Ω2Ω2+ψ1(Ω2Ω2+ψ1(Ω2Ω2+ψ1(Ω2Ω2)))) ~~ {n,n(1(1(1''2'')1(1(1(1(1(1(1(1''2'')2')2'')2')2'')2')2'')2')2)2}
ψ(Ω2Ω2×2) = ψ(Ω2Ω2+Ω2) ~~ {n,n(1(1(1''2'')1(1''2'')2')2)2}
ψ(Ω2Ω2×3) ~~ {n,n(1(1(1''2'')1(1''2'')1(1''2'')2')2)2}
ψ(Ω2Ω2×ω) ~~ {n,n(1(1(2''2'')2')2)2}
ψ(Ω2Ω2×ψ(Ω2Ω2)) ~~ {n,n(1(1(1(1(1(1''2'')2')2)2''2'')2')2)2}
ψ(Ω2Ω2×Ω) ~~ {n,n(1(1(1'2''2'')2')2)2}
ψ(Ω2Ω2×ψ1(Ω2Ω2)) ~~ {n,n(1(1(1(1(1''2'')2')2''2'')2')2)2}
ψ(Ω2Ω2×ψ1(Ω2Ω2×ψ1(Ω2Ω2))) ~~ {n,n(1(1(1(1(1(1(1''2'')2')2''2'')2')2''2'')2')2)2}
ψ(Ω2Ω2×ψ1(Ω2Ω2×ψ1(Ω2Ω2×ψ1(Ω2Ω2)))) ~~ {n,n(1(1(1(1(1(1(1(1(1''2'')2')2''2'')2')2''2'')2')2''2'')2')2)2}
ψ(Ω2Ω22) = ψ(Ω2Ω2×Ω2) ~~ {n,n(1(1(1''3'')2')2)2} = {n,n(1(1(1(1(1(1(1...2''2'')2')2''2'')2')2''2'')2')2)2} - где n-вложений
ψ(Ω2Ω23) ~~ {n,n(1(1(1''4'')2')2)2}
ψ(Ω2Ω2ω) ~~ {n,n(1(1(1''1,2'')2')2)2}
ψ(Ω2Ω2ψ(ΩΩΩ)) ~~ {n,n(1(1(1''1(1(1'1'2')2)2'')2')2)2}
ψ(Ω2Ω2ψ(Ω2Ω2ψ(ΩΩΩ))) ~~ {n,n(1(1(1''1(1(1(1''1(1(1'1'2')2)2'')2')2)2'')2')2)2}
ψ(Ω2Ω2Ω) ~~ {n,n(1(1(1''1'2'')2')2)2}
ψ(Ω2Ω2ψ1(Ω2))) ~~ {n,n(1(1(1''1(1''2')2'')2')2)2}
ψ(Ω2Ω2ψ1(Ω2Ω2))) ~~ {n,n(1(1(1''1(1(1''2'')2')2'')2')2)2}
ψ(Ω2Ω2ψ1(Ω2Ω2×Ω))) ~~ {n,n(1(1(1''1(1(1'2''2'')2')2'')2')2)2}
ψ(Ω2Ω2ψ1(Ω2Ω2ω))) ~~ {n,n(1(1(1''1(1(1''1,2'')2')2'')2')2)2}
ψ(Ω2Ω2ψ1(Ω2Ω2Ω))) ~~ {n,n(1(1(1''1(1(1''1'2'')2')2'')2')2)2}
ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2)))) ~~ {n,n(1(1(1''1(1(1''1(1''2')2'')2')2'')2')2)2}
ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2)))) ~~ {n,n(1(1(1''1(1(1''1(1(1''2'')2')2'')2')2'')2')2)2}
ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2×Ω)))) ~~ {n,n(1(1(1''1(1(1''1(1(1'2''2'')2')2'')2')2'')2')2)2}
ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2ω)))) ~~ {n,n(1(1(1''1(1(1''1(1(1''1,2'')2')2'')2')2'')2')2)2}
ψ(Ω2Ω2ψ1(Ω2Ω2ψ1(Ω2Ω2Ω)))) ~~ {n,n(1(1(1''1(1(1''1(1(1''1'2'')2')2'')2')2'')2')2)2}
ψ(Ω2Ω2Ω2) ~~ {n,n(1(1(1''1''2'')2')2)2} = {n,n(1(1(1''1(1(1''1(1(1''1...2'')2')2'')2')2'')2')2)2} - где n-вложений
ψ(Ω2Ω2Ω2×2) ~~ {n,n(1(1(1''1''2'')3')2)2}
ψ(Ω2Ω2Ω2×ω) ~~ {n,n(1(1(1''1''2'')1,2')2)2}
ψ(Ω2Ω2Ω2×Ω) ~~ {n,n(1(1(1''1''2'')1'2')2)2}
ψ(Ω2Ω2Ω2+1) = ψ(Ω2Ω2Ω2×Ω2) ~~ {n,n(1(1(1''1''2'')1''2')2)2}
ψ(Ω2Ω2Ω2+Ω) ~~ {n,n(1(1(1''1''2'')1(1'2'')2')2)2}
ψ(Ω2Ω2Ω2+Ω2) ~~ {n,n(1(1(1''1''2'')1(1''2'')2')2)2}
ψ(Ω2Ω2Ω2+Ω22) ~~ {n,n(1(1(1''1''2'')1(1''3'')2')2)2}
ψ(Ω2Ω2Ω2×2) ~~ {n,n(1(1(1''1''2'')1(1''1''2'')2')2)2}
ψ(Ω2Ω2Ω2×ω) ~~ {n,n(1(1(2''1''2'')2')2)2}
ψ(Ω2Ω2Ω2+1) = ψ(Ω2Ω2Ω2×Ω2) ~~ {n,n(1(1(1''2''2'')2')2)2}
ψ(Ω2Ω2Ω2×2) ~~ {n,n(1(1(1''1''3'')2')2)2}
ψ(Ω2Ω2Ω22) ~~ {n,n(1(1(1''1''1''2'')2')2)2}
ψ(Ω2Ω2Ω2ω) ~~ {n,n(1(1(1(2'')2'')2')2)2}
ψ(Ω2Ω2Ω2Ω) ~~ {n,n(1(1(1(1'2'')2'')2')2)2}
ψ(Ω2Ω2Ω2Ω2) ~~ {n,n(1(1(1(1''2'')2'')2')2)2}
ψ(5Ω2) ~~ {n,n(1(1(1(1"1''2'')2'')2')2)2}
ψ(6Ω2) ~~ {n,n(1(1(1(1(1"2'')2'')2'')2')2)2}
ψ(7Ω2) ~~ {n,n(1(1(1(1(1"1"2'')2'')2'')2')2)2}
ψ(8Ω2) ~~ {n,n(1(1(1(1(1(1"2'')2'')2'')2'')2')2)2}
ψ(Ω3) = ψ(εΩ2+1) ~~ {n,n(1(1(1(1(1(...(1"2'')...)2'')2'')2'')2')2)2} - где n/2 вложений для четных n
ψ(Ω3) = ψ(εΩ2+1) ~~ {n,n(1(1(1(1(1(...(1"1"2'')...)2'')2'')2'')2')2)2} - где (n-1)/2 вложений для нечетных n
ψ(Ω3) = ψ(εΩ2+1) ~~ {n,n(1(1(1'''2'')2')2)2}
ψ(Ω3)+1 ~~ {n,n(2(1(1'''2'')2')2)2}
ψ(Ω3)×2 ~~ {n,n(1(1(1(1'''2'')2')2)2(1(1'''2'')2')2)2}
ψ(Ω3+1) = ψ(Ω3)×ω ~~ {n,n(1(1(1(1'''2'')2')2)1,2(1(1'''2'')2')2)2}
ψ(Ω3+ψ(Ω)) ~~ {n,n(1(1(1(1'''2'')2')2)1(1'2)2(1(1'''2'')2')2)2}
ψ(Ω3+ψ(Ω2)) ~~ {n,n(1(1(1(1'''2'')2')2)1(1(1''2')2)2(1(1'''2'')2')2)2}
ψ(Ω3+ψ(Ω3)) ~~ {n,n(1(1(1(1'''2'')2')2)1(1(1(1'''2'')2')2)2(1(1'''2'')2')2)2}
ψ(Ω3+Ω) = εψ(Ω3)+1 ~~ {n,n(1'2(1(1'''2'')2')2)2}
ψ(Ω3+ψ1(Ω2)) ~~ {n,n(1(1''2')2(1(1'''2'')2')2)2}
ψ(Ω3+ψ1(Ω2×2)) ~~ {n,n(1(1''3')2(1(1'''2'')2')2)2}
ψ(Ω3+ψ1(Ω3)) ~~ {n,n(1(1(1'''2'')2')3)2}
ψ(Ω3+Ω2) ~~ {n,n(1(1''2(1'''2'')2')2)2}
ψ(Ω3+Ω22) ~~ {n,n(1(1''1''2(1'''2'')2')2)2}
ψ(Ω3+Ω23) ~~ {n,n(1(1''1''1''2(1'''2'')2')2)2}
ψ(Ω3+Ω2ω) ~~ {n,n(1(1(2'')2(1'''2'')2')2)2}
ψ(Ω3+Ω2Ω2) ~~ {n,n(1(1(1''2'')2(1'''2'')2')2)2}
ψ(Ω3+Ω2Ω2Ω2) ~~ {n,n(1(1(1''1''2'')2(1'''2'')2')2)2}
ψ(Ω3+Ω2Ω2Ω2Ω2) ~~ {n,n(1(1(1(1''2'')2'')2(1'''2'')2')2)2}
ψ(Ω3+ψ2(Ω3)) ~~ {n,n(1(1(1'''2'')3')2)2}
ψ(Ω3+ψ2(Ω3)×2) ~~ {n,n(1(1(1'''2'')4')2)2}
ψ(Ω3+ψ2(Ω3+1)) ~~ {n,n(1(1(1'''2'')1,2')2)2}
ψ(Ω3+ψ2(Ω3+Ω)) ~~ {n,n(1(1(1'''2'')1'2')2)2}
ψ(Ω3+ψ2(Ω3+Ω2)) ~~ {n,n(1(1(1'''2'')1''2')2)2}
ψ(Ω3+ψ2(Ω3+ψ2(Ω3))) ~~ {n,n(1(1(1'''2'')1(1'''2'')2')2)2}
ψ(Ω3+ψ2(Ω3+ψ2(Ω3+1))) ~~ {n,n(1(1(2'''2'')2')2)2}
ψ(Ω3+ψ2(Ω3+ψ2(Ω3+Ω))) ~~ {n,n(1(1(1'2'''2'')2')2)2}
ψ(Ω3+ψ2(Ω3+ψ2(Ω3+Ω2))) ~~ {n,n(1(1(1''2'''2'')2')2)2}
ψ(Ω3+ψ2(Ω3+ψ2(Ω3+ψ2(Ω3)))) ~~ {n,n(1(1(1(1'''2'')2'''2'')2')2)2}
ψ(Ω3×2) = ψ(Ω3+Ω3) ~~ {n,n(1(1(1'''3'')2')2)2}
ψ(Ω3×ω) ~~ {n,n(1(1(1'''1,2'')2')2)2}
ψ(Ω3×Ω) ~~ {n,n(1(1(1'''1'2'')2')2)2}
ψ(Ω3×Ω2) ~~ {n,n(1(1(1'''1''2'')2')2)2}
ψ(Ω3×Ω2×ω) ~~ {n,n(1(1(1'''1''1,2'')2')2)2}
ψ(Ω3×Ω2×Ω) ~~ {n,n(1(1(1'''1''1'2'')2')2)2}
ψ(Ω3×Ω22) = ψ(Ω3×Ω2×Ω2) ~~ {n,n(1(1(1'''1''1''2'')2')2)2}
ψ(Ω3×Ω2Ω) ~~ {n,n(1(1(1'''1(1'2'')2'')2')2)2}
ψ(Ω3×Ω2Ω2) ~~ {n,n(1(1(1'''1(1''2'')2'')2')2)2}
ψ(Ω3×ψ2(Ω3)) ~~ {n,n(1(1(1'''1(1'''2'')2'')2')2)2}
ψ(Ω3×ψ2(Ω3×ψ2(Ω3))) ~~ {n,n(1(1(1'''1(1'''1(1'''2'')2'')2'')2')2)2}
ψ(Ω32) = ψ(Ω3×Ω3) ~~ {n,n(1(1(1'''1'''2'')2')2)2} = {n,n(1(1(1'''1(1'''1(1'''...2'')2'')2'')2')2)2} - где n-вложений
ψ(Ω32×2) ~~ {n,n(1(1(1'''1'''3'')2')2)2}
ψ(Ω33) ~~ {n,n(1(1(1'''1'''1'''2'')2')2)2}
ψ(Ω33×2) ~~ {n,n(1(1(1'''1'''1'''3'')2')2)2}
ψ(Ω3ω) ~~ {n,n(1(1(1(2''')2'')2')2)2}
ψ(Ω3ψ(Ω3ω)) ~~ {n,n(1(1(1(1(1(1(1(2''')2'')2')2)2''')2'')2')2)2}
ψ(Ω3ψ(Ω3ψ(Ω3ω))) ~~ {n,n(1(1(1(1(1(1(1(1(1(1(1(2''')2'')2')2)2''')2'')2')2)2''')2'')2')2)2}
ψ(Ω3Ω) ~~ {n,n(1(1(1(1'2''')2'')2')2)2} = {n,n(1(1(1(1(1(1(1(1...2''')2'')2')2)2''')2'')2')2)2} - где n-вложений
ψ(Ω3Ω×Ω) ~~ {n,n(1(1(1(1'2''')2'')1'2')2)2}
ψ(Ω3Ω×Ω2) ~~ {n,n(1(1(1(1'2''')2'')1''2')2)2}
ψ(Ω3Ω+1) = ψ(Ω3Ω×Ω3) ~~ {n,n(1(1(1(1'2''')2'')1'''2')2)2}
ψ(Ω3ψ1(Ω2)) ~~ {n,n(1(1(1(1(1''2')2''')2'')2')2)2}
ψ(Ω3ψ1(Ω2Ω2)) ~~ {n,n(1(1(1(1(1(1''2'')2')2''')2'')2')2)2}
ψ(Ω3ψ1(Ω3)) ~~ {n,n(1(1(1(1(1(1'''2'')2')2''')2'')2')2)2}
ψ(Ω3ψ1(Ω3ω)) ~~ {n,n(1(1(1(1(1(1(2''')2'')2')2''')2'')2')2)2}
ψ(Ω3ψ1(Ω3ψ1(Ω3ω))) ~~ {n,n(1(1(1(1(1(1(1(1(1(2''')2'')2')2''')2'')2')2''')2'')2')2)2}
ψ(Ω3Ω2) ~~ {n,n(1(1(1(1''2''')2'')2')2)2} = {n,n(1(1(1(1(1(1(1...2''')2'')2')2''')2'')2')2)2} - где n-вложений
ψ(Ω3Ω2×Ω) ~~ {n,n(1(1(1(1''2''')2'')1'2')2)2}
ψ(Ω3Ω2×Ω2) ~~ {n,n(1(1(1(1''2''')2'')1''2')2)2}
ψ(Ω3Ω2+1) = ψ(Ω3Ω2×Ω3) ~~ {n,n(1(1(1(1''2''')2'')1'''2')2)2}
ψ(Ω3ψ2(Ω3)) = ψ(Ω2εΩ2+1) ~~ {n,n(1(1(1(1(1'''2'')2''')2'')2')2)2}
ψ(Ω3ψ2(Ω3ω)) ~~ {n,n(1(1(1(1(1(2''')2'')2''')2'')2')2)2}
ψ(Ω3ψ2(Ω3Ω2)) ~~ {n,n(1(1(1(1(1(1''2''')2'')2''')2'')2')2)2}
ψ(Ω3ψ2(Ω3ψ2(Ω3ω))) ~~ {n,n(1(1(1(1(1(1(1(2''')2'')2''')2'')2''')2'')2')2)2}
ψ(Ω3ψ2(Ω3ψ2(Ω3Ω2))) ~~ {n,n(1(1(1(1(1(1(1(1''2''')2'')2''')2'')2''')2'')2')2)2}
ψ(Ω3ψ2(Ω3ψ2(Ω3ψ2(Ω3ω)))) ~~ {n,n(1(1(1(1(1(1(1(1(1(2''')2'')2''')2'')2''')2'')2''')2'')2')2)2}
ψ(Ω3ψ2(Ω3ψ2(Ω3ψ2(Ω3Ω2)))) ~~ {n,n(1(1(1(1(1(1(1(1(1(1''2''')2'')2''')2'')2''')2'')2''')2'')2')2)2}
ψ(Ω3Ω3) ~~ {n,n(1(1(1(1'''2''')2'')2')2)2} = {n,n(1(1(1(1(1(1(1(1...2''')2'')2''')2'')2''')2'')2')2)2} - где n-вложений
ψ(Ω3Ω32) = ψ(Ω3Ω3×Ω3) ~~ {n,n(1(1(1(1'''3''')2'')2')2)2}
ψ(Ω2Ω2ω) ~~ {n,n(1(1(1(1'''1,2''')2'')2')2)2}
ψ(Ω3Ω3Ω) ~~ {n,n(1(1(1(1'''1'2''')2'')2')2)2}
ψ(Ω3Ω3Ω2) ~~ {n,n(1(1(1(1'''1''2''')2'')2')2)2}
ψ(Ω3Ω3ψ2(Ω3Ω3Ω2))) ~~ {n,n(1(1(1(1'''1(1(1'''1''2''')2'')2''')2'')2')2)2}
ψ(Ω3Ω3ψ2(Ω3Ω3ψ2(Ω3Ω3Ω2)))) ~~ {n,n(1(1(1(1'''1(1(1'''1(1(1'''1''2''')2'')2''')2'')2''')2'')2')2)2}
ψ(Ω3Ω3Ω3) ~~ {n,n(1(1(1(1'''1'''2''')2'')2')2)2} = {n,n(1(1(1(1'''1(1(1'''1(1(1'''1...2''')2'')2''')2'')2''')2'')2')2)2} - где n-вложений
ψ(Ω3Ω3Ω3Ω3) ~~ {n,n(1(1(1(1(1'''2''')2''')2'')2')2)2}
ψ(5Ω3) ~~ {n,n(1(1(1(1(1'''1'''2''')2''')2'')2')2)2}
ψ(6Ω3) ~~ {n,n(1(1(1(1(1(1"'2''')2''')2''')2'')2')2)2}
ψ(7Ω3) ~~ {n,n(1(1(1(1(1(1'''1'''2''')2''')2''')2'')2')2)2}
ψ(8Ω3) ~~ {n,n(1(1(1(1(1(1(1'''2''')2''')2''')2''')2'')2')2)2}
ψ(Ω4) = ψ(εΩ3+1) ~~ {n,n(1(1(1(1(1(1(...(1'''2''')...)2''')2''')2''')2'')2')2)2} - где n/2 вложений для четных n
ψ(Ω4) = ψ(εΩ3+1) ~~ {n,n(1(1(1(1(1(1(...(1'''1'''2''')...)2''')2''')2''')2'')2')2)2} - где (n-1)/2 вложений для нечетных n
ψ(Ω4) = ψ(εΩ3+1) ~~ {n,n(1(1(1(1''''2''')2'')2')2)2}
ψ(Ω4Ω4) ~~ {n,n(1(1(1(1(1''''2'''')2''')2'')2')2)2}
ψ(Ω5) = ψ(εΩ4+1) ~~ {n,n(1(1(1(1(1'''''2'''')2''')2'')2')2)2}
ψ(Ω5Ω5) ~~ {n,n(1(1(1(1(1(1'''''2''''')2'''')2''')2'')2')2)2}
ψ(Ω6) = ψ(εΩ5+1) ~~ {n,n(1(1(1(1(1(1''''''2''''')2'''')2''')2'')2')2)2}
ψ(Ω6Ω6) ~~ {n,n(1(1(1(1(1(1(1''''''2'''''')2''''')2'''')2''')2'')2')2)2}
ψ(Ωω) = ψ(sup(Ωn)|n<ω) ~~ {n,n(1(1(1(1(1(1(1...2'''''')2''''')2'''')2''')2'')2')2)2} - где n вложений и в каждом n штрихов
Теперь, давайте я приведу еще какую-нибудь функцию, которая соответствует достигнутой нами скорости роста. Эта функция будет модификацией, уже рассмотренной нами ранее, другой функции, а именно связанной с игрой в сражение с гидрой. Тогда устройство гидры и правила сражения с ней описывала теорема Кирби-Париса, которая утверждала, что гарантированная победа над описанной гидрой доказывает, что ординал ε0 является PTO для Аксиом Пеано Арифметики первого порядка. Так вот есть намного более опасная гидра, сражение и гарантированная победа над которой доказывает, что Ординал Бухольца ψ(Ωω) является PTO для Аксиом подсистемы П11-CA0 Арифметики второго порядка. Теорему, которая утверждает об этом, сформулировал и доказал сам Вильфред Бухольц.
Итак давайте уже разбирать правила игры. Так же как и у гидры Кирби-Париса у гидры Бухольца головы могут расти не только из туловища, но и из других голов. Однако в добавок к этому каждая голова отмечена неким произвольным числом. Туловище не имеет номера, а каждая из голов, которая приклеплена непосредственно к туловищу обязательно имеет номер "0". Ну и по-прежнему отрубать головы можно только если от них не растут другие головы, и головы отрубленные от туловища больше не вырастают. Однако если отрубить голову не растущую непосредственно от туловища, а растущую из другой головы, то гидра будет отращивать головы по более хитрым правилам нежели гидра Кирби-Париса. Давайте так же формально запишем эти правила:
Создание гидры для сражения:
Туловище - R - не имеет номера и условно отмечается знаком "+",
головы прикрепленные к туловищу имеют номер - 0,
остальные головы имеют произвольный номер - x,
Правила сражения:
Голова - a,
Узел, к которому она крепится - b,
Узел, к которому крепится этот узел - с,
и т.д.
Регенеративная способностью гидры - h.
Если мы отрубаем голову a, то:
1) если голова имеет номер 0 и прикреплена к туловищу (b = R) - ничего не происходит.
2) если голова имеет номер 0 и прикреплена к некому узлу, который не является туловищем (b ≠ R) - тогда от узла c создается h копий всего древа, которое осталось на узле c после отрубания головы.
3) если голова имеет номер x+1 и прикреплена к некому узлу, который не является туловищем (b ≠ R) - тогда спускаемся вниз по древу до тех пор пока не найдется голова n с номером y, таким что y ≤ x (которая гарантированно существует, ведь каждая голова прикрепленная к туловищу имеет номер 0). После чего мы создаем копию этого древа, у которого номер узла n' меняем на x, a номер отрубленной головы a' меняем на 0, и помещаем его на место отрубленной головы a.
Как вы заметили помимо ранее известных нам двух правил, по которым гидра могла отращивать головы только вширь и не могла расти вверх, добавилось третье правило связанное с числами, которыми отмечают ее головы, и оно позволяет ей расти вверх. Но несмотря на то, что такая гидра может расти вверх, номера которыми отмечаются ее головы стабильно убывают при сражении с ней, значит она вполне уязвима и эту гидру можно победить за конечное количество ходов. Мы можем так же изобразить эту гидру при помощи скобок, как будто бы это вид на нее сверху, например так: (+(0(2)(1))). И получается что, если все головы отмечены нулями, то такая гидра не будет отличаться от гидры Кирби-Париса, поэтому я не вижу смысла демонстрировать отрубание головы отмеченной числом "0", это происходит так же как на рисунке №55, приведенном в прошлой части. Давайте лучше наглядно рассмотрим, что произойдет при отрубании головы отмеченной неким числом не равным нулю.
рис.67
Не буду вдаваться в подробности того как именно обязательное наличие выигрышной стратегии в сражении с такой гидрой доказывает что ψ(Ωω) является PTO для подсистемы П11-CA0, все-таки мы занимаемся гугологией, а не теорией доказательств и не ординальным анализом. В двух словах скажу только что головы отмеченные нулями ассоциируют с натуральными числами, головы отмеченные ненулевыми числами n ассоциируют с множествами натуральных чисел, такими что они эквивалентны формуле содержащей n однотипных кванторов, ну и отталкиваясь от этого методом трансфинитной индукции создается весьма сложное доказательство, которое я конечно же не буду здесь приводить.
Намного интереснее будет разобрать быстрорастущую функцию основанную на этой игре, которую так и называют гидрой Бухольца. Пусть мы имеем гидру в виде линейного графа высотой n+1 (головы растут из голов по одной, тогда n+1 - число голов), у которой числом n отмечена каждая голова, кроме первой (первая, как мы помним, по правилам должна быть отмечена нулем), функция BH(n) определяет сколько понадобится ходов, чтобы победить эту гидру, при условии, что регенеративная способность гидры h = 1, и растет на единицу h = h+1 с каждым ходом. Функция растет очень быстро, так BH(0) = 1, что вполне естественно, BH(1) = 5, что легко показать: (+(0(1))); (+(0(0))); (+(0)(0)(0)); (+(0)(0)); (+(0)). А вот BH(2) уже невозможно вычислить, но по приблизительной оценке это значение должно быть меньше чем fε0(5). В целом, как следует из теоремы Бухольца, скорость роста функции соответствует уровню ψ(Ωω), причем, начиная с n = 3, по мере того как мы увеличиваем n, скорость роста функции должна соответствовать очередному уровню коллапсирующей функции Бухольца для получения соответствующего данной скорости роста счетного ординала.
Мы уже находимся на таких скоростях роста, что обычно их считают достаточными, так например, аксиоматическую подсистему П11-CA0 арифметики второго порядка, считают достаточной для использования во всех практических областях математики. То есть, как оказывается, пресловутая теория множеств сформулированная в аксиоматической системе ZFC, способная вывести всю используемую нами математику в рамках единых аксиом, на практике оказывается чересчур сильной теорией и даже ее младшая сестра - полная система аксиом арифметики второго порядка Z2, в которой мы можем оперировать лишь множествами из натуральных чисел, тоже слишком сильная теория. Программа, учрежденная уже знакомым нам Харви Фридманом, и именуемая реверсивной математикой, идет по обратному пути в отличие от программы Гильберта, вместо того чтобы вывести единую систему аксиом, реверсивная математика изучает все теоремы, которыми мы пользуемся и пытается понять какой системы аксиом достаточно, чтобы теорема нормально доказывалась и работала. Так вот, за 40 лет существования этой программы математики выяснили что, оказывается, подсистемы П11-CA0 арифметики второго порядка вполне достаточно, чтобы вся используемая нами математика вполне себе хорошо работала практически в любом прикладном применении. Поэтому даже серьезный ординальный анализ выше П11-CA0, как считают многие математики, становится лишь теоретической забавой. Но мы то это сразу не скрывали, что гугология для нас это занимательная наука, поэтому продолжаем, да и как я говорил, ординальная коллапсирующая функция Бухольца на ординале ψ(Ωω) еще не останавливается, и приведенное нами определение функции может создать куда бо́льшие счетные ординалы.
Я думаю, многим уже стало очевидно как именно можно продолжить Функцию Бухольца. Раз в ординале ψ(Ωω) уже задействован несчетный ординал с кардинальностью ω - первого трансфинитного орадинала (|ωω| =ℵω), то ничто не мешает нам подставлять в функцию и кардиналы имеющие бо́льшую трансфинитную кардинальность, например ℵω+1, ℵω×2, ℵε0, ℵψ(Ωω), и т.д. Тогда мы должны определить и соответствующие им коллапсирующие подфункции с трансфинитным порядковым номером, чтобы цепь коллапсирования тоже стала трансфинитной, и в отличие скажем от трансфинитных значений тетрации, определение такого инструмента для создания счетных ординалов не вызовет никаких проблем. Но перед тем как окунаться с головой в глубокую трансфинитную кардинальность, давайте проследим как будет выглядеть в рамках коллапсирующей функции переход хотя бы от ψ(Ωω) к ψ(Ωω+1). Ну первые шаги в соответствии с правилами ординальной арифметики и правилами коллапсирования будут весьма просты и понятны: ψ(Ωω+1) = ψ(Ωω)×ω; ψ(Ωω+ψ(Ωω)) = ψ(Ωω)ψ(Ωω); ψ(Ωω+ψ(Ωω+ψ(Ωω))) = ψ(Ωω)ψ(Ωω)ψ(Ωω); ψ(Ωω+Ω) = α↦ψ(Ωω+α) = ψ(Ωω+ψ(Ωω+ψ(Ωω+...))) = ωψ(Ωω) = εψ(Ωω)+1. Так мы получим ψ(Ωω) зарекурсированный до пределов аксиом арифметики первого порядка, а вот ψ(Ωω) зарекурсированный до Бахмановского уровня это не ψ(Ωω+Ω2), как можно было бы подумать а всего лишь ψ(Ωω+ψ1(Ω2)) = ψ(Ωω+εΩ+1), и я уже объяснял почему первый ординал должен быть больше. Дальше переберем следующие ординалы: ψ(Ωω+ψ1(εΩ2+1)) = ψ(Ωω+ψ1(Ω3)); ψ(Ωω+ψ1(ψ2(εΩ3+1))) = ψ(Ωω+ψ1(Ω4)); ψ(Ωω+ψ1(ψ2(ψ3(εΩ4+1))) = ψ(Ωω+ψ1(Ω5)); ... и в итоге получим: ψ(Ωω+ψ1(Ωω)) = ψ(Ωω+ ψ1(ψ2(ψ3(ψ4(ψ5(...)))))). И только лишь такая бесконечная цепочка вложений ψ(Ωω+α↦ψ1(Ωω+α)) = ψ(Ωω+ψ1(Ωω+ψ1(Ωω+ψ1(...)))) будет диагонализироваться так ψ(Ωω+Ω2), ну а следующие n-ные неподвижные точки этого вложения будут выражаться уже так ψ(Ωω+Ω2×n). Следующая схема продвижения строится по тому же принципу: ψ(Ωω+εΩ2+1) = ψ(Ωω+ψ2(Ω3)); ψ(Ωω+ψ2(εΩ3+1)) = ψ(Ωω+ψ2(Ω4)); ψ(Ωω+ψ2(ψ3(εΩ4+1))) = ψ(Ωω+ψ2(Ω5)); ... и так далее до ψ(Ωω+ψ2(Ωω)) = ψ(Ωω+ψ2(ψ3(ψ4(ψ5(...))))), после чего спустя бесконечную цепочку вложений ψ(Ωω+ψ2(Ωω+ψ2(Ωω+ψ2(...)))) получим ψ(Ωω+α↦ψ2(Ωω+α)) = ψ(Ωω+Ω3). В целом, я думаю, шаблон рекурсии понятен, и тогда после бесконечной череды ординалов: ψ(Ωω+ψ3(Ωω+ψ3(Ωω+ψ3(...)))) = ψ(Ωω+Ω4); ψ(Ωω+ψ4(Ωω+ψ4(Ωω+ψ4(...)))) = ψ(Ωω+Ω5); ...; ψ(Ωω+ψn(Ωω+ψn(Ωω+ψn(...)))) = ψ(Ωω+α↦ψn(Ωω+α)) = ψ(Ωω+Ωn+1) - можно определить: ψ(Ωω×2) = ψ(Ωω+Ωω) = ψ(Ωω+sup(ψn(Ωω)|n<ω)). После чего необходимо пройти такую же череду рекурсий только для умножения ψ(Ωω×ε0) = ψ(Ωω×ψ(Ω)); ψ(Ωω×Ω) = α↦ψ(Ωω×α) = ψ(Ωω×ψ(Ωω×ψ(Ωω×...))); ψ(Ωω×ψ1(Ω2)) = ψ(Ωω×εΩ+1); ψ(Ωω×Ω2) = ψ(Ωω×α↦ψ1(Ωω×α)) = ψ(Ωω×ψ1(Ωω×ψ1(Ωω×ψ1(...)))); или в общем случае ψ(Ωω×Ωn+1) = ψ(Ωω×α↦ψn(Ωω×α)) = ψ(Ωω×ψn(Ωω×ψn(Ωω×ψn(...)))), и ψ(Ωω2) = ψ(Ωω×Ωω) = ψ(Ωω×sup(ψn(Ωω)|n<ω)). Ну и для степени мы так же должны придерживаться тех же правил рекурсирования: ψ(ΩωΩ) = α↦ψ(Ωωα) = ψ(Ωωψ(Ωωψ(Ωω...))); ψ(ΩωΩ2) = ψ(Ωωα↦ψ1(Ωωα)) = ψ(Ωωψ1(Ωωψ1(Ωω...))); ...; ψ(ΩωΩn+1) = ψ(Ωωα↦ψn(Ωωα)) = ψ(Ωωψn(Ωωψn(Ωω...))), чтобы получить ψ(ΩωΩω) = ψ(Ωωsup(ψn(Ωω)|n<ω)). Ну а дальше пределом последовательности {Ωω, ΩωΩω, ΩωΩωΩω, ΩωΩωΩωΩω, ...} и станет ψ(ΩωΩωΩωΩω...) = ψ(εΩω+1) = ψ(Ωω+1) - счетный ординал получаемый коллапсированием из несчетного ординала со следующей трансфинитной кардинальностью (|ωω+1| =ℵω+1). Это важный ординал, у которого тоже есть свое собственное имя, но подробнее о нем мы поговорим потом, давайте сначала до конца разберем возможности ординальной коллапсирующей функции Бухольца.
Прежде чем продолжать, я должен сказать, что иногда промежуточные коллапсирующие фунции записывают так: ψ0(n) = ψΩ1(n), ψ1(n) = ψΩ2(n), ψ2(n) = ψΩ3(n), и т.д., ψk(n) = ψΩk+1(n), где индекс функции символизирует последнее коллапсирование, после которого следует прервать череду коллапсирования. Такая запись дана в определении коллапсирующей функции и такая запись будет более корректной, поскольку как мы теперь знаем серию промежуточных коллапсирующих функций можно продолжить до трансфинитного уровня, поэтому давайте пользоваться этой более корректной записью, чтобы не запутаться в трансфинитных коллапсирующих подфункциях. Тогда продолжая рекурсии над ψ(Ωω+1), по правилам ординальной колапсирующей функции мы должны записать выражение ψ(Ωω+1)ψ(Ωω+1) = ψ(Ωω+1+ψ(Ωω+1)) = ψ(Ωω+1+ψ0(Ωω+1)) так ψ(Ωω+1+ψΩ1(Ωω+1)), где "ψΩ1(Ωω+1)" - значит, что коллапсирование ординала ωω+1 остановится на сильно зарекурсированном ординале с кардинальностью ℵ0, что в сущности эквивалентно ψ(Ωω+1). Тогда ψ(Ωω+1+ψ1(Ωω+1)) = ψ(Ωω+1+ψΩ2(Ωω+1)), где "ψΩ2(Ωω+1)" - значит уже, что коллапсирование ординала ωω+1 остановится на сильно зарекурсированном ординале с кардинальностью ℵ1, и так далее, пока не получим ψ(Ωω+1+ψω(Ωω+1)) = ψ(Ωω+1+ψΩω+1(Ωω+1)), где "ψΩω+1(Ωω+1)" - значит, что коллапсирование ординала ωω+1 остановится на ординале с кардинальностью ℵω, а именно ψ(Ωω+1+ψΩω+1(Ωω+1)) = ψ(Ωω+1+εΩω+1). Однако это не равносильно выражению ψ(Ωω+1×2) = ψ(Ωω+1+Ωω+1), чтобы получить его мы должны сделать так ψ(Ωω+1+α↦ψΩω+1(Ωω+1+α)) = ψ(Ωω+1+ψΩω+1(Ωω+1+ψΩω+1(Ωω+1+...))) и это в соответствии с правилами ординальной коллапсирующий функции будет эквивалентно ψ(εΩω+2). Дальше процесс рекурсирования можно выразить по той же схеме, что мы использовали, когда сравнивали коллапсирование ординалов с конечной кардинальностью.
ψ(Ωω) = ψ0(ψ1(ψ2(ψ3(ψ4(ψ5(...)))))) = ψΩ1(ψΩ2(ψΩ3(ψΩ4(ψΩ5(ψΩ6(...))))))
ψ(εΩω+1) = ψ(ΩωΩωΩωΩω...) = ψ(Ωω+1)
ψ(εΩω+2) = ψ(Ωω+1×2)
ψ(ζΩω+1) = ψ(Ωω+12)
ψ(ζΩω+2) = ψ(Ωω+12×2)
ψ(ГΩω+1) = ψ(Ωω+1Ωω+1)
ψ(φ(1φ(1φ(1...φ(1Ωω10)...)))) = ψ(Ωω+1Ωω+1Ωω+1)
ψ(εΩω+1+1) = ψ(Ωω+1Ωω+1Ωω+1Ωω+1...) = ψ(Ωω+2)
ψ(εΩω+1+2) = ψ(Ωω+2×2)
ψ(ζΩω+1+1) = ψ(Ωω+22)
ψ(ζΩω+1+2) = ψ(Ωω+22×2)
ψ(ГΩω+1+1) = ψ(Ωω+2Ωω+2)
ψ(φ(1φ(1φ(1...φ(1Ωω+110)...)))) = ψ(Ωω+2Ωω+2Ωω+2)
ψ(εΩω+2+1) = ψ(Ωω+2Ωω+2Ωω+2Ωω+2...) = ψ(Ωω+3)
ψ(εΩω+n+1) = ψ(Ωω+nΩω+nΩω+nΩω+n...) = ψ(Ωω+n+1)
ψ(εΩω+n+2) = ψ(Ωω+n+1×2)
ψ(ζΩω+n+1) = ψ(Ωω+n+12)
ψ(ζΩω+n+2) = ψ(Ωω+n+12×2)
ψ(ГΩω+n+1) = ψ(Ωω+n+1Ωω+n+1)
ψ(φ(1φ(1φ(1...φ(1Ωω+n10)...)))) = ψ(Ωω+n+1Ωω+n+1Ωω+n+1)
ψ(εΩω+n+1+1) = ψ(Ωω+n+1Ωω+n+1Ωω+n+1Ωω+n+1...) = ψ(Ωω+n+2)
ψ(Ωω×2) = ψΩ1(ψΩ2(ψΩ3(ψΩ4(ψΩ5(ψΩ6(...ψΩω+1(ψΩω+2(ψΩω+3(ψΩω+4(ψΩω+5(...)))))...))))))
Как можно заметить пределом этой череды рекурсий будет ψ(Ωω×2) = ψ(sup(Ωω+n)|n<ω), так же как ψ(Ωω) был пределом для ψ(sup(Ωn)|n<ω). Дальше будем продвигаться по ординальной коллапсирующей функции скачками, по так называемым предельным кардиналам (понятие предельный ординал/кардинал будет рассмотрено нами далее, но вероятно многие уже поняли что это означает). Следующий предельный кардинал, задействованный в ординальной коллапсирующей функции Бухольца, это ψ(Ωω×3) = ψ(sup(Ωω×2+n)|n<ω), за ним следует другой предельный кардинал ψ(Ωω×4) = ψ(sup(Ωω×3+n)|n<ω), и так далее до ψ(Ωω2) = ψ(sup(Ωω×n)|n<ω). Ну и поскакали дальше: ψ(Ωωω) = ψ(sup(Ωωn)|n<ω); ψ(Ωωωω) = ψ(sup(Ωωωn)|n<ω); ψ(Ωωω) = ψ(sup(Ωnω)|n<ω). Ординал ψ(Ωωω) будет эквивалентен ψ(Ωε0) или, как мы знаем, ψ(Ωψ(Ω)). Ну конечно, раз мы добрались до коллапсирования ординалов с трансфинитной кардинальностью, почему бы нам не задействовать большие счетные ординалы зарекурсированные коллапсирующей функцией, чтобы выразить уровень этой кардинальности. Ну а дальше, я думаю, уже каждый представил себе чем все это закончиться: α↦ψ(Ωα) = ψ(Ωψ(Ωψ(Ωψ(Ωψ(Ω...))))), и, барабанная дробь, мы можем диагонализировать этого монстра ординалом ψ(ΩΩ), так же как когда-то диагонализировали: ψ(ΩΩ) = α↦ψ(Ωα) = ψ(Ωψ(Ωψ(Ωψ(Ωψ(...))))). Что же это за ординал такой получился у нас внутри колласпирующей функции ψ(ΩΩ) - получается что это ординал, кардинальность которого равна ω1 - первому несчетному ординалу (|ωω1| =ℵω1). Ну и как обычно, получается, что последующие n-ные неподвижные точки этой диагонализации будут выражаться так ψ(ΩΩ×n). Но даже не думаем останавливаться на достигнутом, мы можем создать всевозможные и доступные в рамках коллапсирующей функции рекурсии и над этой кардинальностью равной ω1, где ψ(ΩΩ+1) и ψ(ΩεΩ+1) = ψ(ΩψΩ2(Ω2)), это только первые шаги, которые приведут нас к ψ(α↦ΩψΩ2(α)) = ψ(ΩψΩ2(ΩψΩ2(ΩψΩ2(ΩψΩ2(...))))), что мы диагонализируем уже так ψ(ΩΩ2), с использованием ординала, кардинальность которого равна ω2 - второму несчетному ординалу (|ωω2| =ℵω2). Мы по-прежнему используем внутри коллапсирующей функции символы Ω вместо ω1, Ω2 вместо ω2, и так далее Ωn вместо ωn - для обозначения несчетных ординалов или их несчетных кардинальностей, пока что просто смиритесь с этим, я еще не скоро расскажу для чего это нужно. Лучше ускорим темп, и минуя ψ(ΩΩω), ψ(ΩΩε0), ψ(ΩΩψ(Ωω)), ψ(ΩΩψ(ΩΩ)), быстрым и уверенным прыжком достигаем неподвижной точки α↦ψ(ΩΩα) = ψ(ΩΩψ(ΩΩψ(...))), которая диагонализируется ψ(ΩΩΩ) - ординалом, кардинальность которого равна ωω1 (|ωωω1| =ℵωω1). В общем, спускаясь таким образом по нисходящей лестнице кардинальности, мы достигнем ординала, кардинальность которого |ωωωω...| = ℵωωω..., и он в сущности является той самой лестницей алефов: ℵℵℵℵ..., на которой мы остановили свое повествование о больших кардиналах в конце второй части. Это удивительный кардинал. Получается, что его кардинальность по величине равна самому этому кардиналу, и действительно, если мы поставим скобки ℵ(ℵℵℵ...), то убедимся, что в них по-прежнему находится тот же самый кардинал. Так или иначе счетный ординал, который получится в результате коллапсирования лестницы алефов ψ(α↦Ωα) = ψ(ΩΩΩΩ...), и будет пределом для Ординальной коллапсирующей функции Бухольца.
Вот теперь полностью разобрав функцию Бухольца, давайте подробнее остановимся на важных ординалах, которые попадались на нашем пути. Первый такой ординал это ψ(Ωω×ε0), у него нет какого-то особого названия, но он имеет важное значение для возможных рекурсивных формул на множествах натуральных чисел с использованием одного вида кванторов. Если мы примем распространение аксиомы свертывания только на такие формулы, а аксиому индукции оставим без изменений и ограничений, так как она сформулирована в полной арифметике второго порядка, то получим следующие подсистемы арифметики второго порядка: П11-CA или Σ11-CA, в зависимости от используемого типа кванторов в определяемых системой аксиом формулах. Ординал ψ(Ωω×ε0) будет PTO для этих подсистем, что еще раз показывает, что формулировка аксиомы индукции в своем полном виде позволяет в рамках данной системы аксиом создавать намного бо́льшие числа.
Примерно здесь же по скорости роста расположилась еще одна функция связанная с графами, это если так можно выразиться, старшая сестра рассмотренной нами в прошлой части функции TREE(n), основанной на игре, в которой мы сажали лес из графов определенного вида - древ, так чтобы они не были гомеоморфно вложенными. В данной функции тоже нужно сажать лес, так чтобы ни один из предыдущих графов не был бы гомеоморфно вложенным в следующий, но только графы будут немного иной природы. Я не буду еще раз объяснять, что значит гомеоморфная вложенность, если вы забыли, что это значит вернитесь с к функции TREE(n) и еще раз прочитайте про это, для наглядности еще обратите внимание на рисунок №57. Лучше давайте объясню, что же за новый вид графов нам нужен. Их называют субкубические псевдографы, и пожалуй оба слова в определении нуждаются в разъяснении. Начнем с понятия псевдограф. Псевографом - называют такой граф, у которого наличие вершин или ребер необязательно (то есть он может быть несвязанный, это когда все или некоторые вершины необязательно связывать ребрами, или он даже может быть пустым - не содержащим ни ребер ни вершин), вершины этого графа могут быть связаны между собой несколькими ребрами, и могут иметь связующие ребра даже сами с собой. Ну а понятие субкубический - значит, что из одной вершины графа не может выходить более чем три ребра. Рассмотрим примеры субкубических псевдографов наглядно на рисунке №68.
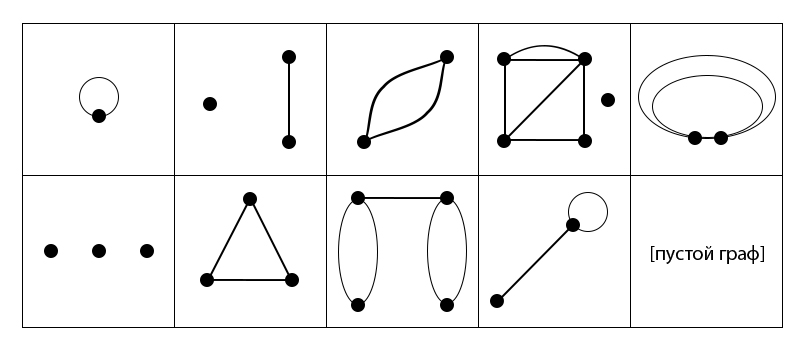
рис.68 (субкубические псевдографы)
Итак, мы сажаем лес таких графов, так чтобы в цепи создаваемых графов не возникало гомеоморфно вложенных. В отличие от древ из функции TREE(n), наши субкубические псевдографы всегда имеют только один вид вершин, но тем не менее, лес все равно может получится очень большой. Так вот размер этого леса зависит от правил посадки, так же как и в случае с функцией TREE(n) мы ограничены количеством вершин, которые можно задействовать в очередном графе, и оно растет на единицу с каждым ходом. Однако, что важно, в этом случае нам разрешено начинать первую посадку не с одной вершины, а с разного количества вершин. Итак, давайте уже сформулируем функцию: SCG(n) - определяет максимально возможное количество субкубических псевдографов, которых можно последовательно создать, так чтобы ни один из предыдущих графов не был бы гомеоморфно вложенным в следующий, при том что на каждом ходу m, нам дозволено создавать граф содержавший не более m+n вершин. Так же как для функции TREE(n) существует теорема Краскала, утверждающая, что функция всегда дает конечное число при любом значении n, так же и для функции SCG(n) существует теорема Робертсона-Сеймура, которая утверждает, что функция всегда дает конечное число при любом значении n. Первое значение функции, когда n = 0, что значит во время хода m можно создать граф с лишь с m вершин, будет равно SCG(0) = 6, и вот такая будет наибольшая последовательность:

рис.69
Обратите внимание, что в соответствии с правилами функции число вершин в каждом графе не превышает его порядковый номер в "лесу". Второе значение функции, когда n = 1, что значит во время хода m можно создать граф лишь с m+1 вершин: SCG(1) - уже столь огромно, что превосходит числа, которые можно создать и разумно записать в рамках аксиом арифметики первого порядка. Мы точно не знаем это значение, пока что его нижняя граница установлена в районе fε0×2+1(3), что значит что SCG(1) точно больше данного числа. Вот пример того "леса", который можно начать садить в SCG(1).
рис.70
На этом рисунке так же можно заметить, что число вершин в каждом графе не превышает его порядковый номер в "лесу" плюс один. Для третьего значения функции, когда n = 2, что значит во время хода m можно создать граф с лишь с m+2 вершин: SCG(2) - установлена нижняя граница в пределах fψ(ΩΩω)+1(3), и если его реальное значение находится ненамного выше этой границы, то получается, что SCG(2) < TREE(3). Однако уже SCG(3) безоговорочно больше, чем TREE(3). Даже приблизительное вычисление определенных значений данной функции сопряжено с большими сложностями, но зато можно делать более надежные прогнозы об общей скорости роста, пока что ее значение оценивается рекурсивной способностью ординала ψ(Ωωω). Так же хочется добавить, что даже если мы запретим создавать графы, в которых вершины могут соединяться более чем одним ребром, и могут замыкать ребра на себя, но оставим возможность графам быть несвязанными, то все равно общая скорость роста функции останется прежней.
Пусть мы не знаем точного значения скорости роста функции SCG(n), но в соответствии с теоремой Робертсона-Сеймура, можно установить верхнюю границу для ее возможной скорости роста, и она будет равна рекурсивной способности ординала ψ(εΩω+1) = ψ(Ωω+1). Как я уже упоминал, это важный ординал в ординальном анализе, и поэтому у него есть свое имя, и это пожалуй самое богатое имя по количеству фамилий математиков в нем. Ординал ψ(εΩω+1) называют Ординалом Такеути-Фефермана-Бухольца (Takeuti-Feferman-Buchholz ordinal). Он является PTO для подсистем П11-CA+BI и Σ11-CA+BI арифметики второго порядка. Это такие подсистемы, которые в аксиоме свертывания определяют работу с формулами на множествах натуральных чисел, в которых задействованы кванторы только одного соответствующего подсистеме вида, и используют аксиому ограничивающей индукции (Bar induction), утверждающей что если что-то справедливо для бесконечной последовательности натуральных чисел, то оно будет справедливо и для любого ее конечного участка.
Мы так же можем еще сильнее модифицировать функцию Гидры Бухольца, если разрешим отмечать головы не только натуральными числами, но и трансфинитными ординалами. Рассмотрим самый простой вариант. Если мы разрешим отмечать головы номером ω, то тогда при отрубании такой головы мы просто меняем ее номер на n+1. Тогда функция будет записываться так BHω(n) - она будет определять количество ходов, необходимое для сражения с гидрой, имеющей n растущих друг из друга голов, отмеченных номером ω, кроме первой головы, которая по-прежнему отмечена нулевым номером. Такая функция будет расти со скоростью эквивалентной рекурсивной способности ординала ψ(Ωω+1) = ψ(εΩω+1) и сам Бухольц доказал это в своей теореме, показав, что построение данной функции невозможно средствами П11-CA+BI. Если мы будем использовать еще бо́льшие ординалы для того чтобы отмечать головы гидры, тогда нам нужно внутри функции разработать систему фундаментальных последовательностей, похожую на ту, которой мы пользуемся когда подставляем ординалы в быстрорастущие иерархии, так чтобы использовать рекурсии, которые в них заложены для создания сверхбольших чисел. Я не буду здесь прописывать такие фундаментальные последовательности для гидры Бухольца, но могу сказать, что предельная возможность таких фундаментальных последовательностей будет ограничена кардинальностью ординала коллапсирующей функции. Так, например, если мы разработаем правила рекурсирования для голов отмеченных ординалом ω+1, то они не позволят нам создать функцию растущую быстрее ψ(Ωω+2). При определении функции в которой головы гидры можно отмечать ω+2, мы так же не сможем превысить скорость роста ψ(Ωω+3). И так далее, думаю, общий принцип понятен.
Если нам удастся определить функцию Гидры Бухольца, в которой головы отмечаются ординалом nω, то мы получим своего рода гибрид Гидры Бухольца и Гидры Кирби-Париса. У такой гидры одно только определение номера, на оставшейся ветке после отрубания головы будет происходить по принципу расчета ходов на сражение с эквивалентной гидрой, у которой все головы отмечены нулями (гидрой Кирби-Париса). Как нетрудно догадаться, такая функция будет расти со скоростью ψ(Ωε0). Этот же ординал будет являться PTO для подсистемы Δ12-CA, в которой аксиома свертывания применима к таким П12-формулам, что их можно выразить через Σ12-формулы или наоборот, при том что аксиома индукции сформулирована в своем неограниченном виде, так же как в полной системе аксиом арифметики второго порядка.
Ну а если мы продолжим создавать расширения функции Гидры Бухольца, определяя все новые фундаментальные последовательности для бо́льших ординалов, то на ординале ψ(ΩΩ) мы получим схождение рекурсий с функциями быстрорастущей иерархии. Я уже объяснял, что такое схождение рекурсий, это когда при подстановке в разные функции одинаковых аргументов n, одна все же растет быстрее другой, но подставив n+1, в ту что росла медленнее, она всегда обгонит первую функцию, что росла быстрее, если у той оставить аргумент n без изменений. В нашем случае аргументы функции - это ординалы используемые для определения фундаментальных последовательностей. Так вот, Гидра Бухольца, в которой определены фундаментальные последовательности на ординале ψ(ΩΩ), будет расти быстрее любой быстрорастущей иерархии, однако ψ(ΩΩ)+1 подставленный в любую быстрорастущую иерархию всегда обгонит Гидру Бухольца, определенную на ψ(ΩΩ). Поэтому, начиная с этого ординала, уже не имеет смысла усиливать Гидру Бухольца ординалами, ибо мы получим практически ту же по силе рекурсию, что заложена в самом ординале.
Так же ординал ψ(ΩΩ) является пределом для расширений массивной нотации Криса Бёрда. Того, кто продолжил развитие массивной нотацию, определив метод расширяющихся массивов. Начиная с ординала ψ(Ωω), он попытался усилить свой метод, используя разделители вложенного расширения, но данный подход был уже достаточно слабым для такого уровня рекурсий, и не продвинул его дальше ψ(ΩΩ), поэтому мы не будем рассматривать этот метод. В поисках более сильной рекурсии мы обратимся к расширениям математика известного под псевдонимом Hypcos, в которых он использовал, как он сам назвал его, метод конечно-последовательного сбрасывания массивов. Этот метод создает невероятно сильные рекурсии, которые на порядок превосходят возможности ординальной коллапсирующей функции Бухольца, и мы до них еще доберемся.
А пока, перед тем как переходить к данному методу, давайте еще раз взглянем на предел этих возможностей коллапсирующей функции Бухольца, которым является ординал ψ(α↦Ωα) = ψ(ΩΩΩΩ...). Этот ординал, тоже важная веха в ординальном анализе, он является PTO для подсистем аксиом Σ11-TR0 и П11-TR0 арифметики второго порядка, то есть, таких систем, в которых аксиома свертывания применима только для формул на множествах натуральных чисел с одним видом кванторов, а аксиома индукции, хоть и сформулирована как в арифметике первого порядка, но позволяет применять ее к трансфинитным ординалам. Интересен тот факт, что в отличие от подсистем арифметики второго порядка, применимых лишь к формулам с ограниченными кванторами, когда аксиома ограничивающей индукции делала эти подсистемы сильнее чем аксиома трансфинитной индукции (PTO П10-TR0 и Σ10-TR0 = ψ(ΩΩ); PTO П10-CA+BI и Σ10-CA+BI = ψ(εΩ+1)), в случае с подсистемами применимыми к формулам с неограниченными кванторами все наоборот - аксиома трансфинитной индукции делает их сильнее чем сделала бы аксиома ограничивающей индукции (PTO П11-CA+BI и Σ11-CA+BI = ψ(εΩω+1); PTO П11-TR0 и Σ11-TR0 = ψ(ΩΩΩΩ...)).
Чтобы еще раз наглядно проследить уровень достигнутой рекурсии, нам нужен очередной блок сравнений. Для этого давайте разбирать новое расширение массивной нотации: Первично нисходящую массивную нотацию. Но перед введением очередного расширения давайте немного модифицируем прежнее расширение: Множественно расширяющуюся массивную нотацию. Многие могли заметить, что в последнем блоке сравнений запись некоторых выражений массивной нотации избыточно сложная, когда нам становится необходимо отображать, что внутри разделителей первичного расширения находятся разделители вторичного расширения, а внутри них разделители третичного расширения, и так далее. Hypcos предложил упростить систему записи, добавив в определение нотации понятие GA-value (grave accents value) - величина разделяющих апострофов. Давайте я приведу ниже формальное определение данной модификации:
Модификация Множественно расширяющейся массивной нотации
Добавлено в определение:
GA-value (“grave accents value”) - величина разделяющих апострофов.
Разделители без апострофов в левой верхней позиции перед закрывающейся скобкой имеют GA-value равное 0, а разделители с m апострофами в левой верхней позиции перед закрывающейся скобкой имеют GA-value равное m+1. При этом сами по себе обычные m-ные апострофы “ ''...' ”, которые выражают (1''...') имеют GA-value равное m.
Изменен:
Случай B2: Если это M = “ ''...' ” - m-ной апостроф, тогда:
1) изменяем “M n” (это вхождение и данный разделитель) на “M 2 M n-1”.
2) пусть t это слой, на котором находится M, и пусть разделитель At = Bt = M
3) повторяем:
а. вычесть 1 из t.
b. пусть разделитель Bt находится в слое t и в нем находится M.
с. если t = 1, то переходим к следующему пункту иначе повторяем этот пункт.
4) находим максимальный t, такой, чтобы разделитель At имел GA-value меньшее, чем m-1.
5) если At имеет GA-value равное m-1, тогда:
а. пусть строки P и Q будут такими, что Bt = “P M Q”
b. изменяем Bt на Sb, где b - итератор, S1 - “,” - запятая, и Si+1 = “P 1 Si 2 Q”
c. закончить и перейти к проверке правил.
6) если At имеет GA-value меньшее, чем m-1, тогда:
а. пусть строки P и Q будут такими, что Bt = “P Bt+1 Q”
b. изменяем Bt на “P(1 At+1 2''...')Q” c m-1 апострофов “ ''...' ” вверху сразу перед закрывающейся скобкой “)”.
закончить и перейти к проверке правил.
Первоначальное авторство: Hypcos, 2015 год.
приложение 19 (Модификация Множественно расширяющейся массивной нотации)
Эта модификация позволяет кратко записывать такие выражения {n,n(1(1''2')2)2} = {n,n(1''2)2}; {n,n(1(1(1'''2'')2')2)2} = {n,n(1'''2)2}; {n,n(1(1(1(1''''2''')2'')2')2)2} = {n,n(1''''2)2} и так далее. Записи при этом остаются уникальными, и однозначно вычисляющимися в соответствии с правилами нотации, а наличие вложенности n-ичного расширения теперь подразумевается автоматически. Ну а самое главное это помогает создавать дальнейшие расширения нотации, которые так же можно будет кратко записать.
Естественно, первое что приходит на ум, когда задумываешься о том как можно расширить нотацию, это диагнолизация n-ичности расширения, для этого можно использовать вхождения и разделители на этой самой n-ичности расширения, таким путем и пошел Бёрд в своем последнем расширении. В используемой нами записи это бы выглядело так ψ(Ωω) ~~ {n,n(1'1,22)2} = {n,n(1''...'2)2} - где n - апострофов. Дальше, минуя очередной круг рекурсий уровня ψ(Ωω), мы могли достичь ψ(Ωω+1) ~~ {n,n(1'2,22)2}. Далее ψ(Ωω×2) ~~ {n,n(1'1,32)2}; ψ(Ωω2) ~~ {n,n(1'1,32)2}; ψ(Ωε0) = ψ(Ωψ(Ω)) ~~ {n,n(1'1(1'2)22)2}. Ну а дальше чередой вложений ψ(Ωψ(Ωψ(Ω))) ~~ {n,n(1'1(1'1(1'2)22)22)2}; ψ(Ωψ(Ωψ(Ωψ(Ω)))) ~~ {n,n(1'1(1'1(1'1(1'2)22)22)22)2} добрались бы до ψ(ΩΩ) ~~ {n,n(1'1(1'1(1'1(1'...2)22)22)22)2}, и такое выражения стало последним определенным Бёрдом в его расширениях, хотя он вполне мог бы продолжить свою нотацию, введя диагонализацию на вложении n-ичности расширения, это выглядело бы так ψ(ΩΩ) ~~ {n,n(1'1'22)2}, затем он мог бы ввести диагонализацию на вложении диагонализации на вложении n-ичности расширения: ψ(ΩΩΩ) ~~ {n,n(1'1'1'222)2} и далее: ψ(ΩΩΩΩ) ~~ {n,n(1'1'1'1'2222)2}, и в итоге пределом нотации стал бы ординал ψ(ΩΩΩΩ...) ~~ {n,n(1'1'1'1'...2222)2}. Однако это очень похоже на то как мы ранее пытались усилить схему примитивного расширения массивов. И как оказалось введение первичного расширения массивов, стало намного более продуктивным методом. И похоже, используя подобные усиления для n-ичного расширения мы пытаемся наступить на те же грабли. Как я не устаю повторять, чтобы по-настоящему усилить рекурсию мы должны ввести либо более сильный принцип, либо хотя бы такой же по силе. Более сильный метод, это метод конечно-последовательного сбрасывания массивов определенный Hypcos, но чтобы полностью понять его силу, нужно на его основе ввести хотя бы такой же по силе метод как n-ичное расширение.
Давайте вспомним, что означал " ' " - разделитель первичного разделения. Когда мы вводили его, то утверждали, что он среди всех известных нам разделителей имеет наивысший уровень и расширять разделители надо начинать именно с него. Потом появились " '' " - разделитель вторичного разделения, " ''' " - разделитель третичного разделения, и так далее, и " ' " уже потерял первенство в этой иерархии. Так вот нам нужен новый разделитель, я бы сказал суперразделитель, который создаст иерархию над иерархией. Этот разделитель - " ,, " (двойная запятая) Hypcos назвал 2-разделителем, тогда все разделители уровня " ' " - считаются 1-разделителями. Теперь " ,, " имеет безоговорочный приоритет при расширении. Такое определение приводит к интересной иерархии. Мы по-прежнему имеем, что (1,,1) = (1'1) = (1) = "," так же как, в более общем случае (n,,1) = (n'1) = (n). Однако " ' " = (1,,2) и следовательно (1'2) = (1(1,,2)2). То есть мы можем заменить все эти n-ичные разделители на выражения с 2-разделителем. Ниже покажу как это будет выглядеть, с учетом использования GA-value в n-ичном расширении.
ε0 = ψ(Ω) ~~ {n,n(1'2)2} = {n,n'2}
ε0 = ψ(Ω) ~~ {n,n(1(1,,2)2)2} = {n,n(1,,2)2}
ψ(Ω)+1 ~~ {n,n(2'2)2} = {n,n(2(1,,2)2)2}
ψ(Ω×2) ~~ {n,n(1'3)2} = {n,n(1(1,,2)3)2}
ψ(Ω2) ~~ {n,n(1'1'2)2} = {n,n(1(1,,2)1(1,,2)2)2}
ψ(Ω3) ~~ {n,n(1'1'1'2)2} = {n,n(1(1,,2)1(1,,2)1(1,,2)2)2}
ψ(Ωω) ~~ {n,n(1(2')2)2} = {n,n(1(2,,2)2)2}
ψ(ΩΩ) ~~ {n,n(1(1'2')2)2} = {n,n(1(1(1,,2)2,,2)2)2}
ψ(ΩΩΩ) ~~ {n,n(1(1'1'2')2)2} = {n,n(1(1(1,,2)1(1,,2)2,,2)2)2}
ψ(ΩΩΩΩ) ~~ {n,n(1(1(1'2')2')2)2} = {n,n(1(1(1(1,,2)2,,2)2,,2)2)2}
ψ(Ω2) = ψ(εΩ+1) ~~ {n,n(1(1''2')2)2} = {n,n(1''2)2} = {n,n''2}
ψ(Ω2) = ψ(εΩ+1) ~~ {n,n(1(1(1,,3)2,,2)2)2} = {n,n(1(1,,3)2)2} = {n,n(1,,3)2}
ψ(Ω2)+1 ~~ {n,n(2(1''2')2)2} = {n,n(2(1(1,,3)2,,2)2)2}
ψ(Ω2+ψ1(Ω2)) ~~ {n,n(1(1''2')3)2} = {n,n(1(1(1,,3)2,,2)3)2}
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+1))) ~~ {n,n(1(2''2')2)2} = {n,n(1(2(1,,3)2,,2)2)2}
ψ(Ω2×2) ~~ {n,n(1(1''3')2)2} = {n,n(1(1(1,,3)3,,2)2)2}
ψ(Ω22) ~~ {n,n(1(1''1''2')2)2} = {n,n(1(1(1,,3)1(1,,3)2,,2)2)2}
ψ(Ω2ω) ~~ {n,n(1(1(2'')2')2)2} = {n,n(1(1(2,,3)2,,2)2)2}
ψ(Ω2Ω2) ~~ {n,n(1(1(1''2'')2')2)2} = {n,n(1(1(1(1,,3)2,,3)2,,2)2)2}
ψ(Ω2Ω2Ω2) ~~ {n,n(1(1(1''1''2'')2')2)2} = {n,n(1(1(1(1,,3)1(1,,3)2,,3)2,,2)2)2}
ψ(Ω2Ω2Ω2Ω2) ~~ {n,n(1(1(1(1''2'')2'')2')2)2} = {n,n(1(1(1(1(1,,3)2,,3)2,,3)2,,2)2)2}
ψ(Ω3) = ψ(εΩ2+1) ~~ {n,n(1(1(1'''2'')2')2)2} = {n,n(1'''2)2} = {n,n'''2}
ψ(Ω3) = ψ(εΩ2+1) ~~ {n,n(1(1(1(1,,4)2,,3)2,,2)2)2} = {n,n(1(1,,4)2)2} = {n,n(1,,4)2}
ψ(Ω4) = ψ(εΩ3+1) ~~ {n,n(1(1(1(1''''2''')2'')2')2)2} = {n,n(1''''2)2} = {n,n''''2}
ψ(Ω4) = ψ(εΩ3+1) ~~ {n,n(1(1(1(1(1,,5)2,,4)2,,3)2,,2)2)2} = {n,n(1(1,,5)2)2} = {n,n(1,,5)2}
ψ(Ωω) ~~ {n,n(1(1,,1,2)2)2} = {n,n(1,,1,2)2}
Раньше в предыдущих версиях массивной нотации мы могли совершать бесконечные нисходящие расширения {n,n'2} = {n,n(1'2)2} = {n,n(1(1'2)2)2} = {n,n(1(1(1'2)2)2)2} = … , теперь мы можем записать их так {n,n(1,,2)2} = {n,n(1(1,,2)2)2} = {n,n(1(1(1,,2)2)2)2} = {n,n(1(1(1(1,,2)2)2)2)2} = ... . Ну а возможность кратко выражать n-ичность расширения в разделителе (1,,n) вместе с возможностью такого нисходящего расширения и дает нам метод конечно-последовательного сбрасывания массивов. Продемонстрирую как работает этот метод на самых простых примерах:
ψ(Ω) ~~ {n,n(1,,2)2} = {n,n(1(1,,2)2)2}
ψ(Ω)+1 ~~ {n,n(2,,2)2} = {n,n(2(1,,2)2)2}
ψ(Ωω) ~~ {n,n(1(2,,2)2)2}
ψ(Ω2) ~~ {n,n(1,,3)2} = {n,n(1(1,,3)2)2} = {n,n(1(1(1,,3)2,,2)2)2}
ψ(Ω2)+1 ~~ {n,n(2,,3)2} = {n,n(2(1(1,,3)2,,2)2)2}
ψ(Ω2+ψ1(Ω2+ψ1(Ω2+1))) ~~ {n,n(1(2(1,,3)2,,2)2)2}
ψ(Ω2ω) ~~ {n,n(1(1(2,,3)2,,2)2)2}
ψ(Ω3) ~~ {n,n(1,,4)2} = {n,n(1(1,,4)2)2} = {n,n(1(1(1,,4)2,,2)2)2} = {n,n(1(1(1(1,,4)3,,2)2,,2)2)2}
ψ(Ω3)+1 ~~ {n,n(2,,4)2} = {n,n(2(1(1(1,,4)2,,3)2,,2)2)2}
ψ(Ω3+ψ1(Ω3+ψ1(Ω3+1))) ~~ {n,n(1(2(1(1,,4)2,,3)2,,2)2)2}
ψ(Ω3+ψ2(Ω3+ψ2(Ω3+1))) ~~ {n,n(1(1(2(1,,4)2,,3)2,,2)2)2}
ψ(Ω3ω) ~~ {n,n(1(1(1(2,,4)2,,3)2,,2)2)2}
Ну а дальше можем спокойно наращивать рекурсии по другую сторону от 2-разделителя - " ,, ". Так мы не только легко сможем переписать в одну строку без всяких верхних индексов всевозможные рекурсии, которые могли бы создать с использованием диагонализации n-ичности расширения, но и продолжить их до небывалых масштабов. Пока остановимся на разделителе (1,,1,,2) который будет эквивалентен пределу ψ(ΩΩΩΩ...) ~~ {n,n(1'1'1'1'...2222)2} - метода вложенных диагоналиазций n-ичности расширения. Попробуем добраться до него, поэтапно сравнивая выражения с рекурсивной способностью ординалов порождаемых функцией Бухольца, но сперва как обычно привожу формальное определение текущего расширения: Первично нисходящей массивной нотации. Сразу за ним последует блок сравнений, в котором я жирным выделил процессы конечно-последовательного сбрасывания массивов, именно они позволяют нотации быть такой сильной, поэтому внимательно проследите за тем как они работают.
Первично нисходящая массивная нотация (Primary dropping array notation)
Определение:
Действительны все определения Multiple expanding array notation
“ ,, ” - двойная запятая - это 2-разделитель
“ , ” - является краткой записью (1,,1)
“ ' ” - является краткой записью (1,,2)
“ '' ” - является краткой записью (1,,3)
“ ''' ” - является краткой записью (1,,4)
“ ''...' ” - n-ной апостроф, является краткой записью (1,,n+1)
Двойную запятую “ ,, ” следует считать разделителем самого высокого уровеня.
Тогда бесконечно нисходящая цепь раделителей выглядит так:
lv(,,) > lv((1,,2)) > lv((1(1,,2)2)) > lv((1(1(1,,2)2)2)) > lv((1(1(1(1,,2)2)2)2)) >…
Правила:
Правило 1: (Правило базы - если в массиве два вхождения) {a,b} = ab
Правило 2: (Правило хвоста - если последнее вхождение массива или разделителя равно 1) {# S 1} = {#} или (# S 1) = (#)
Правило 3: (Правило рекурсии - если 2-е и 3-е вхождение не равно 1) {a,b,c #} = {a,{a,b-1,c #},c-1 #}
Правило 4: (Правило свертывания - если lv(S) < lv(S+), для массива или разделителя) {# S 1 S+ #+} = {# B #+} или (# S 1 S+ #+) = (# B #+)
“#” и “#+” - какие-то строки вхождений и разделителей, также могут быть пустыми.
“S” и “S+” - разделители.
“A0” - весь массив.
Процесс:
Циклично и последовательно проверяем выполнение 4-х приведенных выше правил, пока не выполнится первое правило.
Если ни одно из 4-х приведенных выше правил не применяется, то запускается процесс исключений.
Начинаем с 3-ого вхождения:
Случай A: Если вхождение равно 1, тогда переходим к следующему вхождению.
Случай B: Если вхождение не равно 1, тогда смотрим на предыдущий элемент:
Случай B1: Если это запятая “,” тогда:
1) изменяем “1,n” (это вхождение и предыдущую единицу) на “b,n-1”, где b - итератор.
2) изменяем все предыдущие вхождения в базовом слое на a, где a - база.
3) закончить и перейти к проверке правил.
Случай B2: Если это двойная запятая, тогда:
1) пусть d = t и это слой, на котором находится двойная запятая. И пусть разделитель B0 это весь массив.
2) повторяем:
a. вычесть 1 из t.
b. пусть разделитель Bt находится на слое t и в нем находится “,,”.
c. если t = 1, то переходим к следующему пункту иначе повторяем этот пункт.
3) находим максимальный t, такой, чтобы lv(At) < lv(Ad-1).
4) пусть строки X и Y будут такими, что Ad-1 = “X ,, n Y”.
5a) Если lv(At) ≥ lv(“X ,, n-1 Y”), то
a. пусть строки P и Q будут такими, что Bt = “P Ad-1 Q”.
b. изменяем Bt на Sb, где b - итератор, S1 - “,” - запятая, и Si+1 = “P Si Q”.
c. закончить и перейти к проверке правил.
5b) Если lv(At) < lv(“X ,, n-1 Y”), то
a. пусть строки P и Q будут такими, что Bt = “P Bt+1 Q”.
b. изменяем Bt на “P X At+1 2 ,, n-1 Y Q”.
c. закончить и перейти к проверке правил.
Случай B3: Если это разделитель K, не являющийся запятой или двойной запятой, тогда
1) изменяем “K n” на “K 2 K n-1”.
2) установите разделитель At = K, теперь K находится на слое t.
3) переходим к первому вхождению в первом из K.
Случай B4: Если это открывающаяся скобка “(” тогда:
1) изменяем разделитель (n #) на строку Sb, где b это итератор, S1 = “(n-1 #)” и Si+1 = “Si 1 (n-1 #)”.
2) закончить и перейти к проверке правил.
Первоначальное авторство: Hypcos, 2015 год.
приложение 20 (Первично нисходящая массивная нотация)
ψ(Ωω) ~~ {n,n(1,,1,2)2} = {n,n(1(1,,1,2)2)2}
ψ(Ωω)+1 ~~ {n,n(2,,1,2)2} = {n,n(2(1,,1,2)2)2}
ψ(Ωω)+ω ~~ {n,n(1,2,,1,2)2} = {n,n(1,2(1,,1,2)2)2}
ψ(Ωω)+ε0 ~~ {n,n(1(1(1,,2)2)2(1,,1,2)2)2}
ψ(Ωω)×2 ~~ {n,n(1(1(1,,1,2)2)2(1,,1,2)2)2}
ψ(Ωω)×ω = ψ(Ωω+1) ~~ {n,n(1(1(1,,1,2)2)1,2(1,,1,2)2)2}
ψ(Ωω)2 = ψ(Ωω+ψ(Ωω)) ~~ {n,n(1(1(1,,1,2)2)1(1(1,,1,2)2)2(1,,1,2)2)2}
ψ(Ωω)ω = ψ(Ωω+ψ(Ωω+1)) ~~ {n,n(1(2(1,,1,2)2)2(1,,1,2)2)2}
ψ(Ωω)ψ(Ωω) = ψ(Ωω+ψ(Ωω+ψ(Ωω))) ~~ {n,n(1(1(1(1,,1,2)2)2(1,,1,2)2)2(1,,1,2)2)2}
ψ(Ωω)ψ(Ωω)ω = ψ(Ωω+ψ(Ωω+ψ(Ωω+1))) ~~ {n,n(1(1(1(1,,1,2)2)1,2(1,,1,2)2)2(1,,1,2)2)2}
ψ(Ωω)ψ(Ωω)ψ(Ωω) = ψ(Ωω+ψ(Ωω+ψ(Ωω+ψ(Ωω)))) ~~ {n,n(1(1(1(1,,1,2)2)1(1(1,,1,2)2)2(1,,1,2)2)2(1,,1,2)2)2}
εψ(Ωω)+1 = φ(1,ψ(Ωω)+1) = ψ(Ωω+Ω) = ψ(Ωω+ψ(Ωω+ψ(Ωω+ψ(Ωω+...)))) ~~ {n,n(1(1,,2)2(1,,1,2)2)2}
εψ(Ωω)+2 = φ(1,ψ(Ωω)+2) = ψ(Ωω+Ω×2)~~ {n,n(1(1,,2)3(1,,1,2)2)2}
ζψ(Ωω)+1 = φ(2,ψ(Ωω)+1) = ψ(Ωω+Ω2) ~~ {n,n(1(1,,2)1(1,,2)2(1,,1,2)2)2}
ηψ(Ωω)+1 = φ(3,ψ(Ωω)+1) = ψ(Ωω+Ω3) ~~ {n,n(1(1,,2)1(1,,2)1(1,,2)2(1,,1,2)2)2}
φ(ω,ψ(Ωω)+1) = ψ(Ωω+Ωω) ~~ {n,n(1(2,,2)2(1,,1,2)2)2}
Гψ(Ωω)+1 = φ(1,0,ψ(Ωω)+1) = ψ(Ωω+ΩΩ) ~~ {n,n(1(1(1,,2)2,,2)2(1,,1,2)2)2}
φ(1,0,0,ψ(Ωω)+1) = ψ(Ωω+ΩΩ2) ~~ {n,n(1(1(1,,2)3,,2)2(1,,1,2)2)2}
φ(1ωψ(Ωω)+10) = ψ(Ωω+ΩΩω) ~~ {n,n(1(1(1,,2)3,,2)2(1,,1,2)2)2}
ψ(Ωω+εΩ+1) = ψ(Ωω+ψ1(Ω2)) ~~ {n,n(1(1,,3)2(1,,1,2)2)2}
ψ(Ωω+ψ1(εΩ2+1)) = ψ(Ωω+ψ1(Ω3)) ~~ {n,n(1(1,,4)2(1,,1,2)2)2}
ψ(Ωω+ψ1(ψ2(εΩ3+1))) = ψ(Ωω+ψ1(Ω4)) ~~ {n,n(1(1,,5)2(1,,1,2)2)2}
ψ(Ωω+ψ1(ψ2(ψ3(εΩ4+1))) = ψ(Ωω+ψ1(Ω5)) ~~ {n,n(1(1,,6)2(1,,1,2)2)2}
ψ(Ωω+ψ1(Ωω)) = ψ(Ωω+ψ1(ψ2(ψ3(ψ4(ψ5(...)))))) ~~ {n,n(1(1,,1,2)3)2}
ψ(Ωω+ψ1(Ωω)×2) ~~ {n,n(1(1,,1,2)4)2}
ψ(Ωω+ψ1(Ωω)×ω) = ψ(Ωω+ ψ1(Ωω+1)) ~~ {n,n(1(1,,1,2)1,2)2}
ψ(Ωω+εψ1(Ωω)+1) = ψ(Ωω+ ψ1(Ωω+Ω)) ~~ {n,n(1(1,,1,2)1(1,,2)2)2}
ψ(Ωω+ψ1(Ωω+ψ1(Ω2))) = ψ(Ωω+ ψ1(Ωω+εΩ+1)) ~~ {n,n(1(1,,1,2)1(1,,3)2)2}
ψ(Ωω+ψ1(Ωω+ψ1(Ωω))) = ψ(Ωω+ψ1(Ωω+ψ1(ψ2(ψ3(ψ4(ψ5(...))))))) ~~ {n,n(1(1,,1,2)1(1,,1,2)2)2}
ψ(Ωω+ψ1(Ωω+ψ1(Ωω)×2)) ~~ {n,n(1(1,,1,2)1(1,,1,2)1(1,,1,2)2)2}
ψ(Ωω+ψ1(Ωω+ψ1(Ωω)×ω)) = ψ(Ωω+ψ1(Ωω+ψ1(Ωω+1))) ~~ {n,n(1(2,,1,2)2)2} = {n,n(1(2(1,,1,2)2,,2)2)2}
ψ(Ωω+ψ1(Ωω+ψ1(Ωω+Ω))) ~~ {n,n(1(1,,2)2,,1,2)2} = {n,n(1(1(1,,2)2(1,,1,2)2,,2)2)2}
ψ(Ωω+ψ1(Ωω+ψ1(Ωω+ψ1(Ωω)))) ~~ {n,n(1(1(1(1,,1,2)2,,2)2(1,,1,2)2,,2)2)2}
ψ(Ωω+ψ1(Ωω+ψ1(Ωω+ψ1(Ωω+ψ1(...))))) = ψ(Ωω+Ω2) ~~ {n,n(1(1(1,,3)2(1,,1,2)2,,2)2)2}
ψ(Ωω+Ω2+Ω) = εψ(Ωω+Ω2)+1 ~~ {n,n(1(1,,2)2(1(1,,3)2(1,,1,2)2,,2)2)2}
ψ(Ωω+Ω2+ψ1(Ωω+Ω2)) ~~ {n,n(1(1(1,,3)2(1,,1,2)2,,2)3)2}
ψ(Ωω+Ω2×2) ~~ {n,n(1(1(1,,3)3(1,,1,2)2,,2)2)2}
ψ(Ωω+Ω2ω) ~~ {n,n(1(1(2,,3)2(1,,1,2)2,,2)2)2}
ψ(Ωω+Ω2Ω2) ~~ {n,n(1(1(1(1,,3)2,,3)2(1,,1,2)2,,2)2)2}
ψ(Ωω+Ω2Ω22) ~~ {n,n(1(1(1(1,,3)3,,3)2(1,,1,2)2,,2)2)2}
ψ(Ωω+εΩ2+1) = ψ(Ωω+ψ2(Ω3)) ~~ {n,n(1(1(1,,4)2(1,,1,2)2,,2)2)2}
ψ(Ωω+ψ2(εΩ3+1)) = ψ(Ωω+ψ2(Ω4)) ~~ {n,n(1(1(1,,5)2(1,,1,2)2,,2)2)2}
ψ(Ωω+ψ2(ψ3(εΩ4+1))) = ψ(Ωω+ψ2(Ω5)) ~~ {n,n(1(1(1,,6)2(1,,1,2)2,,2)2)2}
ψ(Ωω+ψ2(Ωω)) = ψ(Ωω+ψ2(ψ3(ψ4(ψ5(ψ6(...)))))) ~~ {n,n(1(1(1,,1,2)3,,2)2)2}
ψ(Ωω+ψ2(Ωω)×2) ~~ {n,n(1(1(1,,1,2)4,,2)2)2}
ψ(Ωω+ψ2(Ωω)×ω) = ψ(Ωω+ψ2(Ωω+1)) ~~ {n,n(1(1(1,,1,2)1,2,,2)2)2}
ψ(Ωω+ψ2(Ωω+Ω2)) ~~ {n,n(1(1(1,,1,2)1(1,,3)2,,2)2)2}
ψ(Ωω+ψ2(Ωω+ψ2(Ωω))) ~~ {n,n(1(1(1,,1,2)1(1,,1,2)2,,2)2)2}
ψ(Ωω+ψ2(Ωω+ψ2(Ωω+1))) ~~ {n,n(1(1(2,,1,2)2,,2)2)2} = {n,n(1(1(2(1,,1,2)2,,3)2,,2)2)2}
ψ(Ωω+ψ2(Ωω+ψ2(Ωω+Ω2))) ~~ {n,n(1(1,,3)2,,1,2)2} = {n,n(1(1(1(1,,3)2(1,,1,2)2,,3)2,,2)2)2}
ψ(Ωω+ψ2(Ωω+ψ2(Ωω+ψ2(Ωω)))) ~~ {n,n(1(1(1(1(1,,3)2(1,,1,2)2,,3)2(1,,1,2)2,,3)2,,2)2)2}
ψ(Ωω+ψ2(Ωω+ψ2(Ωω+ψ2(Ωω+ψ2(...))))) = ψ(Ωω+Ω3) ~~ {n,n(1(1(1(1,,4)2(1,,1,2)2,,3)2,,2)2)2}
ψ(Ωω+Ω3+Ω) = εψ(Ωω+Ω3)+1 ~~ {n,n(1(1,,2)2(1(1(1,,4)2(1,,1,2)2,,3)2,,2)2)2}
ψ(Ωω+Ω3+ψ1(Ωω+Ω3)) ~~ {n,n(1(1(1(1,,4)2(1,,1,2)2,,3)2,,2)3)2}
ψ(Ωω+Ω3+Ω2) ~~ {n,n(1(1(1,,3)2(1(1,,4)2(1,,1,2)2,,3)2,,2)2)2}
ψ(Ωω+Ω3+ψ2(Ωω+Ω3)) ~~ {n,n(1(1(1(1,,4)2(1,,1,2)2,,3)3,,2)2)2}
ψ(Ωω+Ω3×2) ~~ {n,n(1(1(1(1,,4)3(1,,1,2)2,,3)2,,2)2)2}
ψ(Ωω+Ω3ω) ~~ {n,n(1(1(1(2,,4)2(1,,1,2)2,,3)2,,2)2)2}
ψ(Ωω+εΩ3+1) = ψ(Ωω+ψ3(Ω4)) ~~ {n,n(1(1(1(1,,5)2(1,,1,2)2,,3)2,,2)2)2}
ψ(Ωω+ψ3(Ωω)) = ψ(Ωω+ψ3(ψ4(ψ5(ψ6(ψ7(...)))))) ~~ {n,n(1(1(1(1,,1,2)3,,3)2,,2)2)2}
ψ(Ωω+ψ3(Ωω+1)) ~~ {n,n(1(1(1(1,,1,2)1,2,,3)2,,2)2)2}
ψ(Ωω+ψ3(Ωω+ψ3(Ωω))) ~~ {n,n(1(1(1(1,,1,2)1(1,,1,2)2,,3)2,,2)2)2}
ψ(Ωω+ψ3(Ωω+ψ3(Ωω+1))) ~~ {n,n(1(1(1(2,,1,2)2,,3)2,,2)2)2} = {n,n(1(1(1(2(1,,1,2)2,,4)2,,3)2,,2)2)2}
ψ(Ωω+ψ3(Ωω+ψ3(Ωω+Ω3))) ~~ {n,n(1(1,,4)2,,1,2)2} = {n,n(1(1(1(1(1,,4)2(1,,1,2)2,,4)2,,3)2,,2)2)2}
ψ(Ωω+ψ3(Ωω+ψ3(Ωω+ψ3(Ωω+ψ3(...))))) = ψ(Ωω+Ω4) ~~ {n,n(1(1(1(1,,5)2(1,,1,2)2,,4)2,,3)2,,2)2}
ψ(Ωω+ψ4(Ωω)) = ψ(Ωω+ψ4(ψ5(ψ6(ψ7(ψ8(...)))))) ~~ {n,n(1(1(1(1(1,,1,2)2,,4)2,,3)2,,2)2)2}
ψ(Ωω+ψ2(Ωω+1)) ~~ {n,n(1(1(1(1(1,,1,2)1,2,,4)2,,3)2,,2)2)2}
ψ(Ωω+ψ4(Ωω+ψ4(Ωω))) ~~ {n,n(1(1(1(1(1,,1,2)1(1,,1,2)2,,4)2,,3)2,,2)2)2}
ψ(Ωω+ψ4(Ωω+ψ4(Ωω+1))) ~~ {n,n(1(1(1(1(2,,1,2)2,,4)2,,3)2,,2)2)2} = {n,n(1(1(1(1(2(1,,1,2)2,,5)2,,4)2,,3)2,,2)2)2}
ψ(Ωω+ψ4(Ωω+ψ4(Ωω+Ω4))) ~~ {n,n(1(1,,5)2,,1,2)2} = {n,n(1(1(1(1(1(1,,5)2(1,,1,2)2,,5)2,,4)2,,3)2,,2)2)2}
ψ(Ωω×2) = ψ(Ωω+Ωω) = ψ(Ωω+sup(ψn(Ωω)|n<ω)) ~~ {n,n(1(1,,1,2)2,,1,2)2}
ψ(Ωω×3) ~~ {n,n(1(1,,1,2)3,,1,2)2}
ψ(Ωω×ω) ~~ {n,n(1(1,,1,2)1,2,,1,2)2}
ψ(Ωω×ε0) = ψ(Ωω×ψ(Ω)) ~~ {n,n(1(1,,1,2)1(1(1,,2)2)2,,1,2)2}
ψ(Ωω×ψ(Ωω)) ~~ {n,n(1(1,,1,2)1(1(1,,1,2)2)2,,1,2)2}
ψ(Ωω×ψ(Ωω×ψ(Ωω))) ~~ {n,n(1(1,,1,2)1(1(1(1,,1,2)2)2,,1,2)2)2,,1,2)2}
ψ(Ωω×Ω) = ψ(Ωω×ψ(Ωω×ψ(Ωω×...))) ~~ {n,n(1(1,,1,2)1(1,,2)2,,1,2)2}
ψ(Ωω×ψ1(Ω2)) ~~ {n,n(1(1,,1,2)1(1(1,,3)2,,2)2,,1,2)2}
ψ(Ωω×ψ1(Ωω)) ~~ {n,n(1(1,,1,2)1(1(1,,1,2)2,,2)2,,1,2)2}
ψ(Ωω×ψ1(Ωω×ψ1(Ωω))) ~~ {n,n(1(1,,1,2)1(1(1(1,,1,2)2,,2)2,,1,2)2,,2)2,,1,2)2}
ψ(Ωω×Ω2) = ψ(Ωω×ψ1(Ωω×ψ1(Ωω×...))) ~~ {n,n(1(1,,1,2)1(1,,3)2,,1,2)2}
ψ(Ωω×Ω3) = ψ(Ωω×ψ2(Ωω×ψ2(Ωω×...))) ~~ {n,n(1(1,,1,2)1(1,,4)2,,1,2)2}
ψ(Ωω2) = ψ(Ωω×Ωω) = ψ(Ωω×sup(ψn(Ωω)|n<ω)) ~~ {n,n(1(1,,1,2)1(1,,1,2)2,,1,2)2}
ψ(Ωω2+Ωω) ~~ {n,n(1(1,,1,2)2(1,,1,2)2,,1,2)2}
ψ(Ωω2+Ωω2) ~~ {n,n(1(1,,1,2)1(1,,1,2)3,,1,2)2}
ψ(Ωω3) ~~ {n,n(1(1,,1,2)1(1,,1,2)1(1,,1,2)2,,1,2)2}
ψ(Ωωω) ~~ {n,n(1(2,,1,2)2,,1,2)2}
ψ(Ωωω+1) ~~ {n,n(1(2,,1,2)1(1,,1,2)2,,1,2)2}
ψ(Ωωω×2) ~~ {n,n(1(2,,1,2)1(2,,1,2)2,,1,2)2}
ψ(Ωωω2) ~~ {n,n(1(3,,1,2)2,,1,2)2}
ψ(Ωωε0) = ψ(Ωωψ(Ω)) ~~ {n,n(1(1(1(1,,2)2)2,,1,2)2,,1,2)2}
ψ(Ωωψ(Ωω)) ~~ {n,n(1(1(1(1,,1,2)2)2,,1,2)2,,1,2)2}
ψ(Ωωψ(Ωωψ(Ωω))) ~~ {n,n(1(1(1(1(1(1,,1,2)2)2,,1,2)2)2,,1,2)2,,1,2)2}
ψ(ΩωΩ) = ψ(Ωωψ(Ωωψ(Ωω...))) ~~ {n,n(1(1(1,,2)2,,1,2)2,,1,2)2}
ψ(Ωωψ1(Ω2)) ~~ {n,n(1(1(1(1,,3)2,,2)2,,1,2)2,,1,2)2}
ψ(Ωωψ1(Ωω)) ~~ {n,n(1(1(1(1,,1,2)2,,2)2,,1,2)2,,1,2)2}
ψ(Ωωψ1(Ωωψ1(Ωω))) ~~ {n,n(1(1(1(1(1(1,,1,2)2,,2)2,,1,2)2,,2)2,,1,2)2,,1,2)2}
ψ(ΩωΩ2) = ψ(Ωωψ1(Ωωψ1(Ωω...))) ~~ {n,n(1(1(1,,3)2,,1,2)2,,1,2)2}
ψ(ΩωΩ3) = ψ(Ωωψ2(Ωωψ2(Ωω...))) ~~ {n,n(1(1(1,,4)2,,1,2)2,,1,2)2}
ψ(ΩωΩω) = ψ(Ωωsup(ψn(Ωω)|n<ω)) ~~ {n,n(1(1(1,,1,2)2,,1,2)2,,1,2)2}
ψ(ΩωΩωΩω) ~~ {n,n(1(1(1,,1,2)1(1,,1,2)2,,1,2)2,,1,2)2}
ψ(ΩωΩωΩωΩω) ~~ {n,n(1(1(1(1,,1,2)2,,1,2)2,,1,2)2,,1,2)2}
ψ(ΩωΩωΩωΩω...) = ψ(εΩω+1) ~~ {n,n(1,,2,2)2} = {n,n(1(1(1(...)2,,1,2)2,,1,2)2,,1,2)2} - где n-вложений
ψ(Ωω+1) = ψ(εΩω+1) = ψ(φ(1,Ωω+1)) ~~ {n,n(1,,2,2)2} = {n,n(1(1,,2,2)2,,1,2)2}
ψ(Ωω+1+Ω) ~~ {n,n(1(1,,2)2(1,,2,2)2,,1,2)2}
ψ(Ωω+1+Ω2) ~~ {n,n(1(1,,3)2(1,,2,2)2,,1,2)2}
ψ(Ωω+1+Ωω) ~~ {n,n(1(1,,1,2)2(1,,2,2)2,,1,2)2}
ψ(Ωω+1+Ωω×2) ~~ {n,n(1(1,,1,2)3(1,,2,2)2,,1,2)2}
ψ(Ωω+1+Ωω2) ~~ {n,n(1(1,,1,2)1(1,,1,2)2(1,,2,2)2,,1,2)2}
ψ(Ωω+1+Ωωω) ~~ {n,n(1(2,,1,2)2(1,,2,2)2,,1,2)2}
ψ(Ωω+1+ΩωΩω) ~~ {n,n(1(1(1,,1,2)2,,1,2)2(1,,2,2)2,,1,2)2}
ψ(Ωω+1+ψΩω+1(Ωω+1)) = ψ(Ωω+1+ΩωΩωΩωΩω...) = ψ(Ωω+1+εΩω+1) ~~ {n,n(1(1(1,,2,2)2,,1,2)2(1,,2,2)2,,1,2)2}
ψ(Ωω+1+ψΩω+1(Ωω+1)×2) ~~ {n,n(1(1(1,,2,2)2,,1,2)3(1,,2,2)2,,1,2)2}
ψ(Ωω+1+ψΩω+1(Ωω+1)×ω) = ψ(Ωω+1+ψΩω+1(Ωω+1+1)) ~~ {n,n(1(1(1,,2,2)2,,1,2)1,2(1,,2,2)2,,1,2)2}
ψ(Ωω+1+ψΩω+1(Ωω+1+Ω)) ~~ {n,n(1(1(1,,2,2)2,,1,2)1(1,,2)2(1,,2,2)2,,1,2)2}
ψ(Ωω+1+ψΩω+1(Ωω+1+Ω2)) ~~ {n,n(1(1(1,,2,2)2,,1,2)1(1,,3)2(1,,2,2)2,,1,2)2}
ψ(Ωω+1+ψΩω+1(Ωω+1+Ωω)) ~~ {n,n(1(1(1,,2,2)2,,1,2)1(1,,1,2)2(1,,2,2)2,,1,2)2}
ψ(Ωω+1+ψΩω+1(Ωω+1+ψΩω+1(Ωω+1))) ~~ {n,n(1(1(1,,2,2)2,,1,2)1(1(1,,2,2)2,,1,2)2(1,,2,2)2,,1,2)2}
ψ(Ωω+1+ψΩω+1(Ωω+1+ψΩω+1(Ωω+1+ψΩω+1(Ωω+1)))) ~~ {n,n(1(1(1(1,,2,2)2,,1,2)2(1,,2,2)2,,1,2)2(1,,2,2)2,,1,2)2}
ψ(Ωω+1×2) = ψ(Ωω+1+ψΩω+1(Ωω+1+ψΩω+1(Ωω+1+...))) ~~ {n,n(1(1,,2,2)3,,1,2)2}
ψ(Ωω+1×2) = ψ(εΩω+2)= ψ(φ(1,Ωω+2)) ~~ {n,n(1(1,,2,2)3,,1,2)2}
ψ(Ωω+1×ω) ~~ {n,n(1(1,,2,2)1,2,,1,2)2}
ψ(Ωω+1×Ω) ~~ {n,n(1(1,,2,2)1(1,,2)2,,1,2)2}
ψ(Ωω+1×Ω2) ~~ {n,n(1(1,,2,2)1(1,,3)2,,1,2)2}
ψ(Ωω+1×Ωω) ~~ {n,n(1(1,,2,2)1(1,,1,2)2,,1,2)2}
ψ(Ωω+1×ψΩω+1(Ωω+1)) = ψ(Ωω+1×ΩωΩωΩωΩω...) = ψ(Ωω+1×εΩω+1) ~~ {n,n(1(1,,2,2)1(1(1,,2,2)2,,1,2)2,,1,2)2}
ψ(Ωω+1×ψΩω+1(Ωω+1×ψΩω+1(Ωω+1))) ~~ {n,n(1(1,,2,2)1(1(1,,2,2)1(1(1,,2,2)2,,1,2)2,,1,2)2,,1,2)2}
ψ(Ωω+12) = ψ(Ωω+1×ψΩω+1(Ωω+1×ψΩω+1(Ωω+1×...))) ~~ {n,n(1(1,,2,2)1(1,,2,2)2,,1,2)2}
ψ(Ωω+12) = ψ(ζΩω+1) = ψ(φ(2,Ωω+1)) ~~ {n,n(1(1,,2,2)1(1,,2,2)2,,1,2)2}
ψ(Ωω+13) = ψ(ηΩω+1) = ψ(φ(3,Ωω+1)) ~~ {n,n(1(1,,2,2)1(1,,2,2)1(1,,2,2)2,,1,2)2}
ψ(Ωω+1ω) = ψ(φ(ω,Ωω+1)) ~~ {n,n(1(2,,2,2)2,,1,2)2}
ψ(Ωω+1Ω) = ψ(φ(Ω,Ωω+1)) ~~ {n,n(1(1(1,,2)2,,2,2)2,,1,2)2}
ψ(Ωω+1Ω2) = ψ(φ(Ω2,Ωω+1)) ~~ {n,n(1(1(1,,3)2,,2,2)2,,1,2)2}
ψ(Ωω+1Ωω) = ψ(φ(Ωω,1)) ~~ {n,n(1(1(1,,1,2)2,,2,2)2,,1,2)2}
ψ(Ωω+1ψΩω+1(Ωω+1)) = ψ(Ωω+1εΩω+1) = ψ(φ(εΩω+1,1)) ~~ {n,n(1(1(1(1,,2,2)2,,1,2)2,,2,2)2,,1,2)2}
ψ(Ωω+1ψΩω+1(Ωω+1ψΩω+1(Ωω+1))) = ψ(φ(φ(εΩω+1,1),0)) ~~ {n,n(1(1(1(1(1(1,,2,2)2,,1,2)2,,2,2)2,,1,2)2,,2,2)2,,1,2)2}
ψ(Ωω+1Ωω+1) = ψ(Ωω+1ψΩω+1(Ωω+1ψΩω+1(Ωω+1ψΩω+1(Ωω+1)...))) = ψ(ГΩω+1) ~~ {n,n(1(1(1,,2,2)2,,2,2)2,,1,2)2}
ψ(Ωω+1Ωω+1Ωω+1) ~~ {n,n(1(1(1,,2,2)1(1,,2,2)2,,2,2)2,,1,2)2}
ψ(Ωω+1Ωω+1Ωω+1Ωω+1) ~~ {n,n(1(1(1(1,,2,2)2,,2,2)2,,2,2)2,,1,2)2}
ψ(εΩω+1+1) = ψ(Ωω+2) ~~ {n,n(1,,3,2)2} = {n,n(1(1(1,,3,2)2,,2,2)2,,1,2)2}
ψ(ζΩω+1+1) = ψ(Ωω+22) ~~ {n,n(1(1(1,,3,2)1(1,,3,2)2,,2,2)2,,1,2)2}
ψ(ГΩω+1+1) = ψ(Ωω+2Ωω+2) ~~ {n,n(1(1(1(1,,3,2)2,,3,2)2,,2,2)2,,1,2)2}
ψ(εΩω+2+1) = ψ(Ωω+3) ~~ {n,n(1,,3,2)2} = {n,n(1(1(1(1,,4,2)2,,3,2)2,,2,2)2,,1,2)2}
ψ(ζΩω+2+1) = ψ(Ωω+32) ~~ {n,n(1(1(1(1,,4,2)1(1,,4,2)2,,3,2)2,,2,2)2,,1,2)2}
ψ(ГΩω+2+1) = ψ(Ωω+3Ωω+3) ~~ {n,n(1(1(1(1(1,,4,2)2,,4,2)2,,3,2)2,,2,2)2,,1,2)2}
ψ(Ωω×2) = ψ(sup(Ωω+n)|n<ω) ~~ {n,n(1,,1,3)2}= {n,n(1(1(1(1...(1,,n,2)...2,,4,2)2,,3,2)2,,2,2)2,,1,2)2} - где n вложений
ψ(Ωω×2+Ω) ~~ {n,n(1(1,,2)2(1,,1,3)2)2}
ψ(Ωω×2+ψ1(Ωω×2)) ~~ {n,n(1(1,,1,3)3)2}
ψ(Ωω×2+Ω2) ~~ {n,n(1(1(1,,3)2(1,,1,3)2,,2)2)2}
ψ(Ωω×2+ψ2(Ωω×2)) ~~ {n,n(1(1(1,,1,3)3,,2)2)2}
ψ(Ωω×2+Ω3) ~~ {n,n(1(1(1(1,,4)2(1,,1,3)2,,3)2,,2)2)2}
ψ(Ωω×2+ψ3(Ωω×2)) ~~ {n,n(1(1(1(1,,1,3)3,,3)2,,2)2)2}
ψ(Ωω×2+Ωω) ~~ {n,n(1(1,,1,2)2,,1,3)2}
ψ(Ωω×2+ψΩω+1(Ωω×2)) ~~ {n,n(1(1(1,,1,3)2,,1,2)2,,1,3)2}
ψ(Ωω×2+Ωω+1) ~~ {n,n(1(1,,2,2)2,,1,3)2}
ψ(Ωω×2+ψΩω+2(Ωω×2)) ~~ {n,n(1(1(1,,1,3)2,,2,2)2,,1,3)2}
ψ(Ωω×2+Ωω+2) ~~ {n,n(1(1,,3,2)2,,1,3)2}
ψ(Ωω×2×2) ~~ {n,n(1(1,,1,3)2,,1,3)2}
ψ(Ωω×2ω) ~~ {n,n(1(2,,1,3)2,,1,3)2}
ψ(εΩω×2+1) = ψ(Ωω×2+1) ~~ {n,n(1,,2,3)2} = {n,n(1(1,,2,3)2,,1,3)2}
ψ(ГΩω×2+1) = ψ(Ωω×2+1Ωω×2+1) ~~ {n,n(1(1(1,,2,3)2,,2,3)2,,1,3)2}
ψ(εΩω×2+1+1) = ψ(Ωω×2+2) ~~ {n,n(1,,3,3)2} = {n,n(1(1(1,,3,3)2,,2,3)2,,1,3)2}
ψ(ГΩω×2+1+1) = ψ(Ωω×2+2Ωω×2+2) ~~ {n,n(1(1(1(1,,3,3)2,,3,3)2,,2,3)2,,1,3)2}
ψ(Ωω×3) = ψ(sup(Ωω×2+n)|n<ω) ~~ {n,n(1,,1,4)2}= {n,n(1(1(1(1...(1,,n,3)...2,,4,3)2,,3,3)2,,2,3)2,,1,3)2} - где n вложений
ψ(Ωω×4) = ψ(sup(Ωω×3+n)|n<ω) ~~ {n,n(1,,1,5)2}= {n,n(1(1(1(1...(1,,n,4)...2,,4,4)2,,3,4)2,,2,4)2,,1,4)2} - где n вложений
ψ(Ωω×5) = ψ(sup(Ωω×4+n)|n<ω) ~~ {n,n(1,,1,6)2}= {n,n(1(1(1(1...(1,,n,3)...2,,4,5)2,,3,5)2,,2,5)2,,1,5)2} - где n вложений
ψ(Ωω2) = ψ(sup(Ωω×n)|n<ω) ~~ {n,n(1,,1,n)2} = {n,n(1,,1,1,2)2}
ψ(Ωω2+1) ~~ {n,n(1,,2,1,2)2}
ψ(Ωω2+ω) ~~ {n,n(1,,1,2,2)2}
ψ(Ωω2×2) ~~ {n,n(1,,1,1,3)2}
ψ(Ωω2×3) ~~ {n,n(1,,1,1,4)2}
ψ(Ωω2×4) ~~ {n,n(1,,1,1,5)2}
ψ(Ωω3) ~~ {n,n(1,,1,1,n)2} = {n,n(1,,1,1,1,2)2}
ψ(Ωω4) ~~ {n,n(1,,1,1,1,n)2} = {n,n(1,,1,1,1,1,2)2}
ψ(Ωωω) = ψ(sup(Ωωn)|n<ω) ~~ {n,n(1,,1(2)2)2}
ψ(Ωωωω) = ψ(sup(Ωωωn)|n<ω) ~~ {n,n(1,,1(1,2)2)2}
ψ(Ωωωωω) = ψ(sup(Ωωωωn)|n<ω) ~~ {n,n(1,,1(1(1)2)2)2}
ψ(Ωωωω...) = ψ(sup(Ωnω)|n<ω) = ψ(Ωε0) = ψ(Ωψ(Ω)) ~~ {n,n(1,,1(1(1,,2)2)2)2}
ψ(ΩГ0) = ψ(Ωψ(ΩΩ)) ~~ {n,n(1,,1(1(1(1,,2)2,,2)2)2)2}
ψ(Ωψ(ΩΩ2)) ~~ {n,n(1,,1(1(1(1,,2)3,,2)2)2)2}
ψ(Ωψ(ΩΩΩ)) ~~ {n,n(1,,1(1(1(1,,2)1(1,,2)2,,2)2)2)2}
ψ(Ωψ(εΩ+1)) = ψ(Ωψ(Ω2)) ~~ {n,n(1,,1(1(1,,3)2)2)2} = {n,n(1,,1(1(1(1(1,,3)2,,2)2)2)2)2}
ψ(Ωψ(ГΩ+1)) = ψ(Ωψ(Ω2Ω2)) ~~ {n,n(1,,1(1(1(1(1(1,,3)2,,3)2,,2)2)2)2)2}
ψ(Ωψ(εΩ2+1)) = ψ(Ωψ(Ω3)) ~~ {n,n(1,,1(1(1,,4)2)2)2} = {n,n(1,,1(1(1(1(1(1,,4)2,,3)2,,2)2)2)2)2}
ψ(Ωψ(ГΩ2+1)) = ψ(Ωψ(Ω3Ω3)) ~~ {n,n(1,,1(1(1(1(1(1(1,,4)2,,4)2,,3)2,,2)2)2)2)2}
ψ(Ωψ(Ωω)) ~~ {n,n(1,,1(1(1,,1,2)2)2)2}
ψ(Ωψ(Ωψ(Ωω))) ~~ {n,n(1,,1(1(1,,1(1(1,,1,2)2)2)2)2)2}
ψ(Ωψ(Ωψ(Ωψ(Ωω)))) ~~ {n,n(1,,1(1(1,,1(1(1,,1(1(1,,1,2)2)2)2)2)2)2)2}
ψ(ΩΩ) = ψ(Ωψ(Ωψ(Ωψ(Ωψ(Ω...))))) = α↦ψ(Ωα) ~~ {n,n(1,,1(1,,2)2)2}
ψ(ΩΩ+Ωω) ~~ {n,n(1(1,,1,2)2,,1(1,,2)2)2}
ψ(ΩΩ+ψΩω+1(Ωω+1)) = ψ(ΩΩ+εΩω+1) ~~ {n,n(1(1(1,,2,2)2,,1,2)2,,1(1,,2)2)2}
ψ(ΩΩ+ψΩω+1(ΩΩ)) ~~ {n,n(1(1(1,,1(1,,2)2)2,,1,2)2,,1(1,,2)2)2}
ψ(ΩΩ+Ωω+1) ~~ {n,n(1(1,,2,2)2,,1(1,,2)2)2}
ψ(ΩΩ+ψΩω+2(Ωω+2)) = ψ(ΩΩ+εΩω+1+2) ~~ {n,n(1(1(1(1,,2,3)2,,2,2)2,,1,2)2,,1(1,,2)2)2}
ψ(ΩΩ+ψΩω+2(ΩΩ)) ~~ {n,n(1(1(1(1,,1(1,,2)2)2,,2,2)2,,1,2)2,,1(1,,2)2)2}
ψ(ΩΩ+Ωω+2) ~~ {n,n(1(1,,2,3)2,,1(1,,2)2)2}
ψ(ΩΩ+Ωω×2) ~~ {n,n(1(1,,1,3)2,,1(1,,2)2)2}
ψ(ΩΩ×2) ~~ {n,n(1(1,,1(1,,2)2)2,,1(1,,2)2)2}
ψ(ΩΩ2) ~~ {n,n(1(1,,1(1,,2)2)1(1,,1(1,,2)2)2,,1(1,,2)2)2}
ψ(ΩΩΩΩ) ~~ {n,n(1(1(1,,1(1,,2)2)2,,1(1,,2)2)2,,1(1,,2)2)2}
ψ(ΩΩΩΩΩΩ) ~~ {n,n(1(1(1,,1(1,,2)2)1(1,,1(1,,2)2)2,,1(1,,2)2)2,,1(1,,2)2)2}
ψ(ΩΩ+1) = ψ(εΩΩ+1) = ψ(ΩΩΩΩΩΩ...) ~~ {n,n(1,,2(1,,2)2)2}
ψ(ГΩΩ+1) = ψ(ΩΩ+1ΩΩ+1) ~~ {n,n(1(1(1,,2(1,,2)2)2,,2(1,,2)2)2,,2(1,,2)2)2}
ψ(ΩΩ+ψ(Ωω)) ~~ {n,n(1,,1(1(1,,1,2)2)2(1,,2)2)2}
ψ(ΩΩ+ψ(ΩΩ)) ~~ {n,n(1,,1(1(1,,1(1,,2)2)2)2(1,,2)2)2}
ψ(ΩΩ+ψ(ΩΩ+1)) ~~ {n,n(1,,1(1(1,,2(1,,2)2)2)2(1,,2)2)2}
ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ))) ~~ {n,n(1,,1(1(1,,1(1(1,,1(1,,2)2)2)2(1,,2)2)2)2(1,,2)2)2}
ψ(ΩΩ×2) = ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ+...))) = α↦ψ(ΩΩ+α) ~~ {n,n(1,,1(1,,2)3)2}
ψ(Ωψ1(Ω2)) = ψ(ΩεΩ+1) ~~ {n,n(1,,1(1(1,,3)2,,2)2)2}
ψ(Ωψ1(ΩΩ)) ~~ {n,n(1,,1(1(1,,1(1,,2)2)2,,2)2)2}
ψ(Ωψ1(Ωψ1(Ω2))) = ψ(ΩΩεΩ+1) ~~ {n,n(1,,1(1(1,,1(1(1,,3)2,,2)2)2,,2)2)2}
ψ(Ωψ1(Ωψ1(ΩΩ))) ~~ {n,n(1,,1(1(1,,1(1(1,,1(1,,2)2)2,,2)2)2,,2)2)2}
ψ(ΩΩ2) = ψ(Ωψ1(Ωψ1(Ωψ1(...)))) = ψ(α↦Ωψ1(α)) ~~ {n,n(1,,1(1,,3)2)2}
ψ(ΩΩ3) = ψ(Ωψ2(Ωψ2(Ωψ2(...)))) = ψ(α↦Ωψ2(α))) ~~ {n,n(1,,1(1,,4)2)2}
ψ(ΩΩω) = ψ(sup(ΩΩn)|n<ω) ~~ {n,n(1,,1(1,,1,2)2)2}
ψ(ΩΩω+1) ~~ {n,n(1,,1(1,,2,2)2)2}
ψ(ΩΩω×2) ~~ {n,n(1,,1(1,,1,3)2)2}
ψ(ΩΩε0) = ψ(ΩΩψ(Ω)) ~~ {n,n(1,,1(1,,1(1(1,,2)2)2)2)2}
ψ(ΩΩψ(Ωω)) ~~ {n,n(1,,1(1,,1(1(1,,1,2)2)2)2)2}
ψ(ΩΩψ(ΩΩ)) ~~ {n,n(1,,1(1,,1(1(1,,1(1,,2)2)2)2)2)2}
ψ(ΩΩΩ) = ψ(ΩΩψ(ΩΩψ(...))) = α↦ψ(ΩΩα) ~~ {n,n(1,,1(1,,1(1,,2)2)2)2}
ψ(ΩΩΩω) ~~ {n,n(1,,1(1,,1(1,,1,2)2)2)2}
ψ(ΩΩΩΩ) ~~ {n,n(1,,1(1,,1(1,,1(1,,2)2)2)2)2}
ψ(ΩΩΩΩω) ~~ {n,n(1,,1(1,,1(1,,1(1,,1,2)2)2)2)2}
ψ(ΩΩΩΩ...) ~~ {n,n(1,,1,,2)2} = {n,n(1,,1(1,,1,,2)2)2} = {n,n(1,,1(1,,1(1,,1(1,,1(...)2)2)2)2)2} - где n вложений
Вот на этом моменте Ординальная коллапсирующая функция Бухольца исчерпала себя, а вот Первичная нисходящая массивная нотация, еще нет и для того чтобы изучать рекурсивный масштаб еще бо́льших выражений, записанных на этой нотации, нам нужные еще бо́льшие счетные ординалы, а для их создания нужна коллапсирующая функция, которая будет работать с еще бо́льшими несчетными ординалами. Но можно ли создать ординал больше, чем тот, что обладает кардинальностю лестницы алефов (|ωωωω...| = ℵωωω...), ведь получается, что он настолько большой, что даже его кардинальность равна по величине самому ординалу (α = ωα). На самом деле можно создать кардиналы еще больше, в теории множеств даже есть такой термин "Большие кардиналы (Large cardinals)", и кардиналы к которым он применяется на самом деле большие, настолько что лестница алефов считается "маленьким кардиналом". Разбирать такие кардиналы и соответствующие им ординалы, а так же способы их коллапсирования мы будем уже в следующей части. А пока я хотел бы еще немного поговорить о коллапсирующей функции, которую мы используем сейчас.
Как я упоминал ранее Ординальная коллапсирующая функция Бухольца это не единственная коллапсирующая функция. Первая коллапсирующая функция была создана Хайнцем Бахманом и она работала несколько по иным правилам, ее пределом был соответственно ординал Бахмана ψ(εΩ+1), поскольку она не включала в свое определение несчетные ординалы с кардинальностью большей чем ℵ1 и соответствующие им дополнительные коллапсирующие функции, но впринципе их легко можно добавить в определение этой функции, тем не менее выражения функции Бухольца и функции Бахмана будут расходится. Так же был математик по имени Соломон Феферман, создавший еще одну коллапсирующую функцию, в ней опять были другие правила, да и использовала она два аругмента, но в отличие от функции Бахмана могла коллапсировать несчетные ординалы с кардинальностями вплоть до ℵω, позже другой математик с созвучной фамилией Андреас Вейерман, изменил функцию Фефермана сократив входящие в нее аргументы до одного и позволив ей работать с трансфинитными кардинальностями. Таким образом мы имеем три коллапсирующие функции, которые позволяют добраться до теоретико-доказательственного ориднала (PTO) подсистем П11-TR0 и Σ11-TR0, причем выражения счетных ординалов записанных с помощью каждой из них будут разными. Читатель уже знакомый с гугологией и коллапсирующими функциями мог сталкивать с не-Бухольцевскими коллапсирующими функциями и вполне обосновано мог негодовать почему созданные коллапсированием счетные ординалы, которые я здесь приводил, отличаются от тех, что он мог видеть раньше. Поэтому здесь в конце этой главы я так же приведу еще расширенную функцию Бахмана и функцию Вейермана, и сопоставление выражений некоторых ординалов для всех трех функций. Обратите внимание, что функции Бухольца и Бахмана принято обозначать одинаковой греческой буквой "ψ" (пси), поэтому, чтобы отличать эти функции, Бахмоновская будет выделена жирным курсивом "ψ".
Расширенная коллапсирующая функция Бахмана для несчетных кардиналов
(Bachmann's Collapsing function of uncountable cardinals)
C0(α,β) = β∪Ωβ∪{0}
Cn+1(α,β) = {γ+δ|γ,δ∈Cn(α,β)}∪{ωΩγ+δ|γ,δ∈Cn(α,β)}∪{ψπ(γ)|π,γ∈Cn(α,β)∧γ<α}
C(α,β) = ∪n<ωCn(α,β)
ψπ(α) = min{β<π|C(α,β)∩π⊆β}
Первоначальное авторство: Хайнц Бахман, 1955 год.
Последующая модификция: Девид Мадоре, 2008 год.
Коллапсирующая функция Вейермана для несчетных кардиналов
(Weiermann's Collapsing function of uncountable cardinals)
C0(α,β) = β
Cn+1(α,β) = {γ+δ,ϑγ(η)|γ,δ,η∈Cn(α,β)∧η<α}
C(α,β) = ∪n<ωCn(α,β)
ϑν(α) = min({β|Ων=|β×ω|∧C(α,β)∩Ων+1⊆β∧α∈C(α,β)})
Первоначальное авторство: Хайнц Бахман, 1955 год.
Последующая модификация: Соломон Феферман, 1987 год.
Последующая модификация: Андреас Вейерман, 2011 год.
Последующая модификация: Deedlit, 2013 год.
Общие определения:
Ω0 = 0
Ωα - минимальный ординал соответствующий несчетному α-ному кардиналу (ℵα)
π - несчетный регулярный кардинал, который может быть записан как Ωα+1
приложение 21 (Ординальные коллапсирующие функции Бахмана и Вейермана)
ε0 = φ(1,0) = ψ(Ω) = ψ(ψ1(0)) = ψ(0) = ϑ(1)
ζ0 = φ(2,0) = ψ(Ω2) = ψ(Ω) = ϑ(2)
η0 = φ(3,0) = ψ(Ω3) = ψ(Ω2) = ϑ(3)
φ(ω,0) = ψ(Ωω) = ψ(Ωω) = ϑ(ω)
φ(1,0,0) = ψ(ΩΩ) = ψ(ΩΩ) = ϑ(Г0) = ϑ(Ω)
φ(1,1,0) = ψ(ΩΩ+1) = ψ(ΩΩ+1) = ϑ(Ω+1)
φ(2,0,0) = ψ(ΩΩ×2) = ψ(ΩΩ×2) = ϑ(Ω×2)
φ(1,0,0,0) = ψ(ΩΩ2) = ψ(ΩΩ2) = ϑ(Ω2)
φ(1,0,0,0,0) = ψ(ΩΩ3) = ψ(ΩΩ3) = ϑ(Ω3)
φ(1,0,0,0,...) = ψ(ΩΩω) = ψ(ΩΩω) = ϑ(Ωω)
ψ(ΩΩΩ) = ψ(ΩΩΩ) = ϑ(ΩΩ)
ψ(ΩΩΩω) = ψ(ΩΩΩω) = ϑ(ΩΩω)
ψ(ΩΩΩΩ) = ψ(ΩΩΩΩ) = ϑ(ΩΩΩ)
ψ(n+1Ω) = ψ(n+1Ω) = ϑ(nΩ)
ψ(εΩ+1) = ψ(Ω2) = ψ(ψ2(0)) = ψ(εΩ+1) = ψ(ψ1(0)) = ϑ(εΩ+1) = ϑ(ϑ1(1))
ψ(ζΩ+1) = ψ(Ω22) = ψ(ζΩ+1) = ψ(Ω2) = ϑ(ζΩ+1) = ϑ(ϑ1(2))
ψ(ηΩ+1) = ψ(Ω23) = ψ(ηΩ+1) = ψ(Ω22) = ϑ(ηΩ+1) = ϑ(ϑ1(3))
ψ(Ω2ω) = ψ(Ω2ω) = ϑ(ϑ1(ω))
ψ(Ω2Ω2) = ψ(Ω2Ω2) = ϑ(ГΩ+1) = ϑ(Ω2)
ψ(εΩ2+1) = ψ(Ω3) = ψ(ψ3(0)) = ψ(εΩ2+1) = ψ(ψ2(0)) = ϑ(εΩ2+1) = ϑ(ϑ2(1))
ψ(ζΩ2+1) = ψ(Ω32) = ψ(ζΩ2+1) = ψ(Ω3) = ϑ(ζΩ2+1) = ϑ(ϑ2(2))
ψ(ηΩ2+1) = ψ(Ω33) = ψ(ηΩ2+1) = ψ(Ω32) = ϑ(ηΩ2+1) = ϑ(ϑ2(3))
ψ(Ω3ω) = ψ(Ω3ω) = ϑ(ϑ2(ω))
ψ(Ω3Ω3) = ψ(Ω3Ω3) = ϑ(ГΩ2+1) = ϑ(Ω3)
ψ(εΩn+1) = ψ(Ωn+1) = ψ(ψn+1(0)) = ψ(εΩn+1) = ψ(ψn(0)) = ϑ(εΩn+1) = ϑ(ϑn(1))
ψ(Ωnm+1) = ψ(Ωnm) = ϑ(ϑn(m))
ψ(Ωnω) = ψ(Ωnω) = ϑ(ϑn(ω))
ψ(Ωω) = ψ(ψΩω(0)) = ϑ(Ωω)
ψ(Ωω2) = ψ(Ωω) = ϑ(Ωω2)
ψ(Ωωω) = ψ(Ωωω) = ϑ(Ωωω)
ψ(ΩωΩω) = ψ(ΩωΩω) = ϑ(ΩωΩω)
ψ(εΩω+1) = ψ(Ωω+1) = ψ(εΩω+1) = ψ(ψΩω+1(0)) = ϑ(εΩω+1) = ϑ(ϑΩω+1(1))
ψ(Ωω+12) = ψ(Ωω+1) = ϑ(ϑΩω+1(2))
ψ(Ωω+1ω) = ψ(Ωω+1ω) = ϑ(ϑΩω+1(ω))
ψ(Ωω+1Ωω+1) = ψ(Ωω+1Ωω+1) = ϑ(ГΩω+1) = ϑ(Ωω+1)
ψ(εΩω+1+1) = ψ(Ωω+2) = ψ(εΩω+1+1) = ψ(ψΩω+2(0)) = ϑ(εΩω+1+1) = ϑ(ϑΩω+2(1))
ψ(Ωω+2Ωω+2) = ψ(Ωω+2Ωω+2) = ϑ(ГΩω+1+1) = ϑ(Ωω+2)
ψ(εΩω+n+1) = ψ(Ωω+n+1) = ψ(εΩω+n+1) = ψ(ψΩω+n+1(0)) = ϑ(εΩω+1+1) = ϑ(ϑΩω+n+1(1))
ψ(Ωω+n+1m+1) = ψ(Ωω+n+1m) = ϑ(ϑΩω+n+1(m))
ψ(Ωω+n+1ω) = ψ(Ωω+n+1ω) = ϑ(ϑΩω+n+1(ω))
ψ(Ωω+n+1Ωω+n+1) = ψ(Ωω+n+1Ωω+n+1) = ϑ(Ωω+n+1)
ψ(Ωω×2) = ψ(ψΩω×2(0)) = ϑ(Ωω×2)
ψ(Ωω×22) = ψ(Ωω×2) = ϑ(Ωω×22)
ψ(Ωω×2ω) = ψ(Ωω×2ω) = ϑ(Ωω×2ω)
ψ(Ωω×2Ωω×2) = ψ(Ωω×2Ωω×2) = ϑ(Ωω×2Ωω×2)
ψ(εΩω×2+1) = ψ(Ωω×2+1) = ψ(εΩω×2+1) = ψ(ψω×2+1(0)) = ϑ(εΩω×2+1) = ϑ(ϑΩω×2(1))
ψ(Ωω×2+1Ωω×2+1) = ψ(Ωω×2+1Ωω×2+1) = ϑ(ГΩω×2+1) = ϑ(Ωω×2+1)
ψ(Ωω×3) = ψ(ψΩω×3(0)) = ϑ(Ωω×3)
ψ(Ωε0) = ψ(Ωψ(Ω)) = ψ(ψψ(0)(0)) = ϑ(Ωε0)
ψ(Ωψ(ΩΩ)) = ψ(ψψ(ΩΩ)(0)) = ϑ(Ωϑ(Г0)) = ϑ(Ωϑ(Ω))
ψ(Ωψ(ΩΩΩ)) = ψ(ψψ(ΩΩΩ)(0)) = ϑ(Ωϑ(ΩΩ))
ψ(Ωψ(εΩ+1)) = ψ(Ωψ(Ω2)) = ψ(ψψ(εΩ+1)(0)) = ψ(ψψ(ψ1(0))(0)) = ϑ(Ωϑ(εΩ+1))
ψ(Ωψ(Ω2Ω2)) = ψ(ψψ(Ω2Ω2)(0)) = ϑ(Ωϑ(ГΩ+1)) = ϑ(Ωϑ(Ω2))
ψ(Ωψ(Ωω)) = ψ(ψψ(ψω(0))(0)) = ϑ(Ωϑ(Ωω))
ψ(Ωψ(Ωψ(Ωω))) = ψ(ψψ(ψψ(ψω(0))(0))(0)) = ϑ(Ωϑ(Ωϑ(Ωω)))
ψ(ΩΩ) = ψ(Ωψ(Ωψ(Ωψ(Ω...)))) = ψ(ψψ1(0)(0)) = ψ(ψψ(ψψ(ψψ(ψ...(0))(0))(0))(0)) = ϑ(ΩΩ) = ϑ(Ωϑ(Ωϑ(Ωϑ(Ω...))))
ψ(ΩΩΩ) = ψ(ψψψ1(0)(0)(0)) = ϑ(ΩΩΩ)
ψ(ΩΩΩΩ...) = ψ(ψψψ...(0)(0)(0)) = ϑ(ΩΩΩΩ...)
На мой взгляд среди трех коллапсирующих функций, функция Бухольца самая удобная, самая интуитивная и самая наглядная, поэтому именно ее мы использовали в сравнениях, и поэтому именно она положена в основу более сильных коллапсирующих функций, которые мы будем разбирать в следующей части, куда я вас и приглашаю, если вы конечно еще не устали от всех этих рекурсий. В любом случае передышка не помешает, ведь дальше уровень рекурсий становится столь головокружительный, что без достаточного понимания главных принципов коллапсирования, в них лучше не погружаться.
следующая часть...