2.3. Там где сходятся дороги

Даже если выяснится, что физика не происходит полностью из математики, это не отменяет того факта, что она от нее сильно зависит и беспрекословно ей подчиняется, как собственно и все остальные науки. Некоторые физические явления особенно из пограничных областей теории относительности и квантовой механики, гораздо легче записать математически, чем представить их в уме. В нашем путешествии мы пытались не касаться математики, по возможности заменяя любые формулы аналогиями. Однако чтобы проникнуть в истинные корни бытия нам придется поговорить о царице наук подробнее.

Сегодня математику воспринимают как скучную отрасль науки, предназначенную исключительно для практических нужд. В этом есть своя правда, математика действительно в большей или в меньшей степени нужна во всех остальных науках. Но только физики сегодня видят в ней ту силу и красоту, которая некогда восхищала мыслителей древности. Математика это область чистой абстракции, проявления которой, так или иначе, встречаются в природе повсюду, но могут ли и сами природные объекты быть проявлениями такой чистой абстракции. Этот вопрос, был задан отнюдь не современными физиками, а он висит в воздухе уже на протяжении тысячелетий. Сегодня математика настолько продвинулась в своем развитии, что ее прикладная часть, использующаяся в описании природы, проектировке инженерных устройств или создании экономических моделей, кажется крайне малой по сравнению с теоретической частью, которая в большинстве своем уже не находит отображений в реальном мире. А раз так, то это лишний раз намекает на то, что наша реальность, сама по себе может быть малой частью математики.

Тем не менее, в современном обществе к математике все сильнее складывается пренебрежительное отношение. Свою роль в этом играет то, что школьников продолжают мучить однотипными задачами, да и в институтах ситуация не лучше, там студентов пичкают обилием терминологии и формул. Однако в математике есть такие вещи, рассказ о которых может удивить не меньше чем повествование физика о черной дыре, а их невероятность с этими черными дырами даже не сравнится. Более того даже в рассказе о черной дыре нельзя избежать привлечения математических понятий, чтобы до человека дошло насколько на самом деле это удивительный объект. В этой последней части книги я постараюсь доступно показать многие чудеса математики, при этом, сильно не перегружая читателя формулами или терминами. Но для начала мы определим, что в математике есть самое фундаментальное.

Математика оперирует многими понятиями, но наиболее важным среди них является множество. Этот термин самый трудноопределимый, хотя его считают наиболее фундаментальным и первичным понятием в математике. Одно из определений множества гласит, что это совокупность элементов воспринимаемых как целое. Тут стоит вспомнить правило, которое сформулировал еще Аристотель, о том, что все многообразие нашего физического мира возникает потому, что система не есть простая сумма ее составляющих, а это нечто новое. Это же является главной характеристикой множества, поэтому с помощью множеств можно описать любые явления нашего мира, чего нельзя сделать, применяя только числа. Теория множеств является фундаментом для всей остальной математики. Все остальные разделы, так или иначе, можно свести к этому, даже наша логика выводится непосредственно из теории множеств.

К примеру, выражение 1+1 нам кажется самым примитивным выражением в математике. Однако компьютеры, например, изначально не понимают, что такое числа и арифметические операции, пока их не запрограммируют на это. В информатике этот процесс называется битностным представлением целочисленных типов данных, и если программа не включает в себя этот алгоритм, то считать она не сможет. Нам же кажется, что 1+1 это просто, лишь потому, что нас мозг устроен так, что используемые нами числа, такие как 1, и арифметические операции, такие как сложение, кажутся ему естественными. С точки зрения теории множеств, которая является фундаментом всей математики, 1+1 это весьма сложная конструкция. Но давайте разберем подробней, почему это так. Начнем с основы основ, с самых базовых аксиом математики, а именно с аксиом теории множеств. Напомню, что аксиомами называются утверждения, принимаемые без доказательств. Я изложу их в немного упрощенном варианте, но основной сути это не изменит.

Начинается теория множеств со следующего утверждения: существуют множества, которые могут содержать элементы. Это утверждение иногда называют нулевой аксиомой, поскольку она просто определяет понятия: множество и элемент. А вот первая аксиома гласит, что если все элементы одного множества принадлежат второму множеству, а все элементы второго множества принадлежат первому – тогда оба множества идентичны. Таким образом, аксиома приводит к выводу, что существует равенство.

Вторая аксиома гласит, что существует, по крайней мере, одно пустое множество (не содержащее элементов) и одно бесконечное множество (содержащее бесконечное число элементов). Таким образом, можно сделать вывод, что множества бывают пустые, конечные и бесконечные. Рассмотрим подробнее, что это значит. Если бесконечное множество элементов еще можно как-то представить то, что значит пустое. Наша логика отказывается с этим соглашаться, ведь если ничего нет, то о каком тогда множестве может идти речь. Тем не менее, математика говорит нам, что даже если ничего нет, все равно существует множество, которое включает в себя это «ничего», поэтому можно сказать, что пустое множество это одно из самых абстрактных понятий, которое включает математика. Кроме того исходя из первой аксиомы следует, что пустое множество единственно. Допустим, вселенная бесконечна в пространстве, тогда мы можем представить разные бесконечные множества, как например бесконечное число звезд, бесконечно число планет и т.д., но «ничего» – оно всегда только одного вида.

Третья аксиома утверждает, что элементы могут принадлежать к разным множествам. Из этой аксиомы следует, что существуют функции – зависимости между элементами множества. А если мы добавим к этому первую аксиому, то это приведет нас к выводу, что существуют подмножества, поскольку множество может включать в себя другие множества или само быть элементом другого множества. Например, имея вагон фруктов, в котором есть ящик яблок можно выделить два множества: собственно фрукты и яблоки. Причем очевидно, что яблоки являются подмножеством фруктов и между этими двумя множествами есть зависимость, ведь если, скажем, испортятся все фрукты, то значит и яблоки, являясь фруктами, испортятся тоже.

Четвертая аксиома звучит следующим образом: каждое суждение об элементах любого множества приводит к образованию другого множества (возможно идентичного исходному). Иными словами аксиома говорит, что существуют: операции – соответствия между множествами, выражаемое через другое множество. Объединив третью и четвертую аксиому, мы получим три базовых операции: объединение, пересечение и отрицание. Покажем, как они работают на примере. Итак, допустим у нас есть железные гвозди и медные гвозди. Соединив два этих множества, мы получим множество гвоздей, это и есть объединение. Исключив из множества гвоздей только железные гвозди, мы получим множество медных гвоздей – это отрицание. Для того чтобы наглядно объяснить, что такое пересечение, добавим еще железные гайки и медные гайки. Так вот среди всего этого обилия металлических предметов множество гвоздей (любых) является пересечением множества железных предметов и множества медных предметов.

Последняя пятая аксиома утверждает, что среди элементов множества может быть порядок. Непосредственный вывод из этой аксиомы это то, что существуют: упорядоченные и неупорядоченные множества, но так же из нее следует и то, что множества могут быть счетными и несчетными, открытыми и замкнутыми. Стоит отметить, что счетные, это не одно и тоже, что упорядоченные. В дальнейшем мы еще коснемся этой темы, но пока поясню, почему это так. Например точки на линии это упорядоченное множество, ибо все они идут в определенном порядке, кроме того оно бесконечное, но несчетное, потому что эти точки нельзя сосчитать, так как мы может отметить их где угодно на линии. Примером замкнутого множества могут служить точки на окружности, хотя оно по-прежнему остается бесконечным, упорядоченным и несчетным.

Собственно нас пока интересуют только упорядоченные множества, с помощью них мы сможем определить понятие числа из чистой абстракции. Для этого нам понадобится еще пустое множество из второй аксиомы. Итак, мы берем пустое множество и сопоставляем его с нулем. Теперь берем другое множество, элементом которого является это пустое множество, и сопоставляем его с единицей. Еще одно множество сопоставим с двойкой, и оно будет включать в себя и пустое множество и то множество, которое включает в себя пустое множество. Так можно продолжать бесконечно, образуя все новые числа. Рождаемые таким образом множества будут упорядоченные, а значит, они полностью соответствуют числам. Получается, что при помощи множеств, мы можем определить понятие числа, но обратное сделать невозможно, и это доказывает первичность множества над числом. Таким же образом определяются и арифметические действия, например, сложение это есть ни что иное как объединение элементов упорядоченных множеств.

Зачем нужны такие сложности, спросите вы. Все это я привел только для того, чтобы вы поняли, какую работу абстрагирования делает ваш мозг за вас, чтобы 1+1 вы воспринимали как нечто естественное и элементарное. Конечно, из аксиом теории множеств можно вывести любое понятие любого раздела математики, но это хорошо только, когда мы пытаемся вывести основы математики из чистой абстракции. Естественно для практических нужд все это выглядит слишком громоздко, и в дальнейшем мы будем отталкиваться от более привычных для нас понятий.

Все числа, которые выводятся вышеописанным образом, называют натуральными. В реальности натуральные числа символизируют дискретность и предметность, то есть описывают элементы, имеющие определяющую черту и выделяющиеся из фона. Поэтому ноль не относят к натуральным числам, поскольку он как раз и символизирует абстрактный хаос или фон, в котором нет ничего определенного. Натуральные числа являются основой для арифметики, знакомство первобытного человека с математикой началось именно с натуральных чисел, ведь это то, с помощью чего мы можем считать. Хоть теория множеств и является более фундаментальной в математике, нежели арифметика, все-таки последняя будет ближе и понятнее читателю. Поэтому свое краткое описание мира математики и его связи с реальностью, я начну именно с нее.

Ключевую роль в арифметике играют не только числа, но и операции, называемые арифметическими действиями. Они имеют уровень* и для их выполнения необходимо два числа. Сложение – это арифметическая операция первого уровня, умножение – второго, степень – третьего. Следующий уровень арифметического действия возникает, когда мы пытаемся обобщить повторяющиеся элементы текущего уровня. Несколько раз сложить одно и то же число, значит умножить, а несколько раз умножить, значит возвести в степень. Кроме того все операции в арифметике имеют обратные действия (вычитание, деление и т.д.) и теряют некоторые свойства с повышением уровня, это есть главная причина, из-за которой возникают другие типы чисел и даже целые другие разделы математики.

Теперь рассмотрим подробнее то, как появляется большинство математических конструкций на основе одной только арифметики. Но перед этим определим, как образуются новые типы чисел. Первый класс чисел, отличающийся от натуральных, возникает в результате обратного сложению действия. Порождаемые в результате вычитания отрицательные числа, символизируют природную неравномерность и неоднородность. Их свойства проявляются в умножении. Задавался ли читатель когда-нибудь вопросом: почему минус, умноженный на минус, дает в результате плюс – в чем разница, почему в этом отношении свойства чисел разнятся. Ведь если представить ось, на которой есть выделенная точка (ноль) и по обе стороны от нее отмечены числа, то почему у такой, казалось бы, идеальной симметрии обнаруживаются разные арифметические свойства чисел. Почему минус, умноженный на минус, равняется плюсу, легко доказывается математически. Не буду приводить доказательство, но скажу, что на уровне логики такая асимметрия заключается в том, что отрицательные числа мы получаем за счет обратного арифметического действия (вычитания), поэтому они считаются «ненастоящими», а значит, симметрия нарушается. Если бы мы писали натуральные числа со знаком «–», и сложение тоже отмечали бы минусом, а вычитание плюсом, то тогда плюс, умноженный на плюс, давал бы минус.

Обратив внимание на деление, которое обратно умножению, мы выясним, что и оно тоже порождает особый тип чисел. Дробным числам так же находится место в реальности, при обозначении частей целого, хотя и тут может встретиться логический парадокс. Мы понимаем что такое клочок бумаги и знаем, что означает выражение половина клочка бумаги. Но в реальности не существует половины клочка бумаги, ведь если мы разорвем его, то получим два клочка бумаги. На самом деле части и дроби это абстракции, не имеющие реально существующих эквивалентов, но с их помощью удобно выражать отношение предметных явлений. Так же хочется отметить, что помимо порождения дробных чисел, деление впервые сталкивает нас с полной невычислимостью, это известное со школы правило о том, что на ноль делить нельзя.

Особую роль в делении играет и единица, если разделить ее на какое-нибудь число, мы получим то, что называют обратной величиной. Так же как любое отрицательное число можно представить в виде произведения положительного числа и минус единицы (например: –15 = –1×15), любое дробное число можно представить в виде произведения числителя и обратной величины знаменателя (например: 8/5 = 8×1/5)*.  Понятие обратной величины очень четко выражено в графике гиперболы (y=1/x), в котором по мере того как одна величина стремится к бесконечности, другая стремится к нулю. Когда гипербола находит отображение в природе, она всегда порождает невероятные явления. Например геометрия черной дыры это проявление гиперболического роста, ведь по мере того как объем внутри нее стремится к нулю, плотность черной дыры стремится к бесконечности. Другой пример гиперболического роста это история нашей вселенной. Изучив начало истории вселенной, мы обнаружим, что чем более ранний момент мы рассматриваем, тем меньший обнаруживаем там объем вселенной и выясняем, что за все меньшие промежутки времени происходили процессы, с другой стороны понимаем, что тем больше были температура и плотность вселенной. Смерть нашей вселенной по современным представлениям будет наоборот замедляющимся процессом. Чем дальше мы вглядываемся в будущее вселенной, тем большим видится ее объем, и прогнозируется, что за все большие промежутки времени будут происходить события, но температура и плотность будут становиться все меньше и меньше. Вот и получается, что история вселенной это гипербола (что и собственно и отображено на графике в главе 1.4).

Вот такие невероятные проявления в реальности создаются за счет простой арифметической операции: деления единицы на число. Но и деление числа на единицу тоже приводит к поразительным следствиям. Известно, что любое число имеет, по крайне мере, два делителя, это единицу и самого себя. Напомню, что делитель это целое число, на которое можно разделить без остатка. Среди натуральных чисел выделяют особую группу, называемую простыми числами, это такие числа, которые кроме единицы и самого себя других делителей не имеют. К ним относят двойку (2/2 = 1, 2/1 = 2 – два делителя), тройку (3/3 = 1, 3/1 = 3 – два делителя), пятерку (5/5 = 1, 5/1 = 5 – два делителя) и так далее. Простое число можно описать как количество предметов, которые поровну можно поделить только на группу из такого же количества человек. Хочется отметить, что саму единуцу к простым числам не относят, потому что у нее всего один делитель, это она сама.

Уникальные свойства простых чисел нашли применение в программировании. Множество сложных алгоритмов построены именно на них, в том числе и механизмы кодирования. Все защитные системы в банках имеют в своей основе задачу разложения числа на простые множители. Компьютеру обычно сложно иметь дело с простыми числами, поэтому на то чтобы подобрать шифр к коду, основанному на простых числах, даже у самого мощного  компьютера могут уйти столетия. Некоторые задачи, основанные на простых числах, компьютер вообще может решать бесконечно долго или решить их ошибочно, хотя человеческий разум легко найдет решение на интуитивном уровне. Квантовые компьютеры, которые сегодня только разрабатываются, в отличие от цифровых систем, должны легко справляться с простыми числами, поэтому у прагматичных специалистов возникают опасения за банковские системы, а специалисты-мечтатели прогнозируют создание искусственного разума на основе квантовых компьютеров. Однако простые числа, несмотря на свое название, могут создать очень непростые задачи даже для человека. Сегодня в математике бóльшая часть недоказанных теорем связана именно с простыми числами. Самая известная среди них теорема Гольдбаха, за доказательство которой назначена премия в миллион долларов. Несмотря на, казалось бы, простую формулировку: «Любое чётное число большее двух можно представить в виде суммы двух простых чисел», люди, которые пытаются проверить истинность этого высказывания, пишут многотомные доказательства, лишь для того, чтобы потом убедится, что все их расчеты были бесплодны.

Продолжая рассматривать арифметические действия, переходим к операциям третьего уровня. Степень отличается от умножения и сложения тем, что имеет два обратных действия (см. таб.10). Так происходит, потому что степень лишена коммунитативности. Многим это непонятное на слух свойство, которое присуще умножению и сложению, знакомо под выражением: от перестановки слагаемых (множителей) сумма (произведение) не меняется. Одна из главных аксиом арифметики заключается в том, что только арифметические действия первых двух уровней (сложение и умножение) обладают коммунитативностью. Степень и арифметические действия высших уровней коммунитативности лишены. Если переставить показатель степени с ее основанием результат изменится. Поэтому у степени два обратных действия: нахождение основания по показателю (корень) и нахождение показателя по основанию (логарифм).

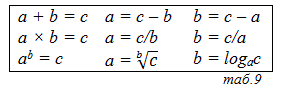
Обычно новые типы чисел в арифметике появляются, когда результат обратной операции невозможно выразить, используя только прежние типы чисел. Однако это правило не распространяется на логарифм, который не может образовывать новых чисел. Если логарифм не решается, то выражение вообще не имеет смысла, так же как деление на ноль. Например, логарифм из 2 по основанию 1, является невычислимым, потому что не может существовать такой степени, возведя в которую единицу, мы получили бы двойку. Зато корень решается почти в любом случае и дает нам целых два новых класса чисел, которые имеют реальный смысл. Наиболее известны из его порождений это иррациональные числа. Например, квадратный корень из двух представляет собой число, которое нельзя записать в виде дроби. Если мы попытаемся представить его в виде десятичной дроби, то у нас будет получаться бесконечный ряд чисел после запятой, расставленных хаотично, без всякой закономерности. Как мы уже выяснили ранее, в такой бесконечной хаотической последовательности, может быть закодирована любая информация. Но, не смотря на свои странные свойства, иррациональные числа оказываются вполне реальными.

Знаменитая теорема Пифагора*, говорит, что если катеты прямоугольного треугольника равны 1, то его гипотенуза будет равна квадратному корню из двух. Несмотря на ее иррациональное значение, мы видим гипотенузу и знаем, что она реальна, хотя и не можем рационально описать ее отношение к катету. Древние греки – лучшие математики античного мира, и то не сразу поняли, что квадратный корень из двух не может быть выражен дробью. Естественно они понимали, что это будет нецелое число и вычислили его приблизительное значение, но поначалу им и в голову не приходило, что квадратный корень из двух невозможно записать дробью. Они считали, что должна существовать какая-то большая дробь, которая будет эквивалентна квадратному корню из двух. Пифагор решил выяснить так ли это. Если увеличить стороны катетов до двух, то гипотенуза будет равна квадратному корню из восьми, что тоже не является целым числом. Пифагор думал, что увеличивая величину катетов, он рано или поздно получит целое число гипотенузы и докажет, что квадратный корень из двух можно записать дробью. Он был полностью обескуражен, когда понял, что в своем эксперименте целого числа он не получит никогда, сколько бы он не увеличивал стороны катетов. Для него это был особенный удар, потому что он верил, что в основе нашего мира лежат целые числа, и что любое явление может быть составлено из отдельных единиц. Но из его эксперимента следовал вывод, что невозможно составить гипотенузу равностороннего прямоугольного треугольника из тех же единиц, из которых составлены катеты, и что в мире существуют числа, не поддающиеся рациональному восприятию (см. рис. 39).

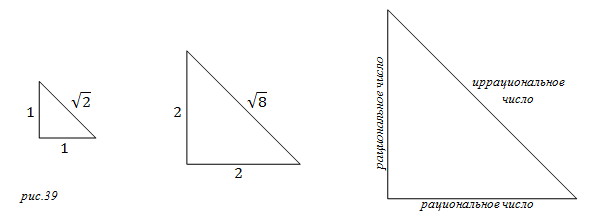
Кроме квадратного корня из двух другим важным иррациональным числом, которое показывает, что иррациональные числа встроены в природу нашего мироздания, является квадратный корень из пяти. Это число иногда называют основой идеала, потому что на основе этого числа выражается, так называемое, золотое сечение. Давайте наглядно представим, что же это такое. Например, у нас есть пирог и нам надо отрезать от него такой кусок, который будет меньше оставшейся части во столько же раз во сколько оставшаяся часть меньше целого пирога. Это и называют золотым сечением. При этом целый пирог будет больше оставшейся части в 1.618033… раз, и оставшаяся часть будет больше отрезанного куска в 1.618033… раз. Или можно сказать наоборот, отрезанный кусок будет меньше в 0.618033… раз оставшейся части, а оставшаяся часть будет в 0.618033… раз меньше пирога. Оба эти числа тоже являются иррациональными, а если мы их сложим, то, как раз, получим квадратный корень из пяти.

Считается, что золотое сечение это основа гармонии в любых видах искусства. Его использовали египтяне при строительстве пирамид и художники эпохи возрождения в живописи (например,  все известные картины Леонардо да Винчи, написаны с использованием пропорций золотого сечения). Золотое сечение есть так же в пропорциях многих чудес света, таких как Ангкор-Ват, Храм Соломона и Собор Василия Блаженного. Задавались ли вы когда-нибудь вопросом, почему пятиконечная звезда кажется нам более идеальной, чем остальные типы звезд, чем она хуже скажем шестиконечных или семиконечных звезд, почему чаще других встречается на флагах, погонах и других знаках и символах разных стран, почему пентаграмма – один из самых часто используемых оккультных символов. Вероятно ответ в том, что все отрезки, которые можно выделить внутри пятиконечной звезды, являются золотым сечением по отношению друг к другу. Значит в нашем восприятии красоты и стремлении к идеалу мы зачастую сами того не ведая используем золотое сечение.

Кроме того золотое сечение можно повсеместно увидеть и в природе, это и раковины улитки, и крылья бабочки, и даже пропорции в строении тела животных и человека, а значит не только человек, но и сама природа стремиться к гармонии. Многие наверно слышали о числах Фиббоначи, которые якобы можно встретить почти в любом природном явлении. Напомню, что числами Фибоначчи называется последовательность, в которой каждое следующее число, есть сумма двух предыдущих (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584…). На самом деле любые проявления чисел Фибоначчи в природе это тоже заслуга золотого сечения. Попробуйте взять одно число Фиббоначи из последовательности и разделить на предыдущее, а затем взять следующее число из последовательности и проделать ту же операцию, тогда вы заметите, что у вас получается результат, который все сильнее и сильнее приближается к золотому сечению (55/34=1.617647…, 89/55=1.618181…, 144/89=1.617977…, 233/144=1.618055…, 377/233=1.618025…, 610/377= 1.618037…), однако его точного значения мы так не достигнем, потому что числа Фиббоначи можно продолжать до бесконечности. Поэтому мы можем по-философски рассудить, что числа Фибоначчи можно рассматривать лишь как стремление к идеалу, который недостижим, поскольку иррационален.

Физическая сущность иррациональных чисел это очень интересный момент, который и сегодня остро стоит в науке. Взять, к примеру, спор между теорией петлевой гравитации, которая настаивает на дискретности пространства-времени и теорией струн, утверждающей, что пространство-время непрерывное. Согласно первой пространство-время это структура из отдельных элементов, которые можно сосчитать, следовательно, пространство-время не может быть описано иррациональными величинами. У теории струн на этот счет противоположная точка зрения, она считает, что пространство-время неделимо на отдельные элементы и может содержать иррациональные величины.

Следуя концепции теории петлевой гравитации, получается, что идеальных равносторонних прямоугольных треугольников в природе начертить невозможно, так же как сделать идеальное золотое сечение. Но с другой стороны возможность делить пространство до бесконечности тоже может вызвать парадокс, который так же впервые осознали еще древние греки. Известна загадка древнегреческого философа Зенона, называемая «Ахиллес и Черепаха». В ней Ахиллес решил пуститься наперегонки с черепахой. Уверенный в своей победе он дает черепахе фору. Но как бы быстро не бежал Ахиллес, и как бы медленно не плелась черепаха, Ахиллесу никогда ее не догнать. Так получается, потому что за то время, которое Ахиллес догоняет черепаху, та успевает уползти еще на некоторое расстояние. И так будет, происходит до бесконечности. В итоге заключил Зенон, что с точки зрения математики движение невозможно.

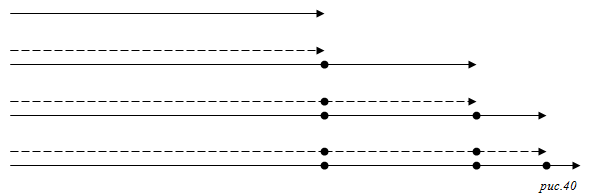
Для наглядности парадокса представим себе весьма шуструю черепаху, которая бегает всего в два раза медленнее Ахиллеса. По парадоксу Зенона, чтобы догнать ее Ахиллес будет постоянно преодолевать половину пути пройденного черепахой, в то время как она будет проходить еще половину от того что успел пробежать Ахиллес (см. рис.40). Например, черепаха пробежала 1 метр, Ахиллес догнал ее, но за это время она успела пробежать еще полметра. Ахиллес преодолел эти полметра, однако черепаха ушла еще на четверть, и так до бесконечности. Получается, что ни Ахиллес, ни черепаха вообще никогда не преодолеют отметку в 2 метра. Решение заключается в том, что  в данной ситуации происходит разложение дистанции в бесконечный ряд: «2=1+1/2+1/4+1/8+1/16+1/32+…». Используя такой математический инструмент, парадокс легко объяснить. Кроме того все иррациональные числа тоже благополучно расписываются в бесконечные ряды и теряют свой шарм загадочности. Например, тот же квадратный корень из двух можно представить как  1+(1/(2+1/(2+1/(2+1/(2+…))))).

Размышление над задачей про Ахиллеса и черепаху, привело математиков к созданию нового раздела математики, называемого математическим анализом. Как правило, описание большинства явлений нашего мира, в том числе связанных с движением, приводит к составлению функций. Мы помним, что с точки зрения теории множеств функция это зависимость между элементами множеств. Чтобы объяснить понятие функции с позиции чисел нужно рассказать, в чем главное отличие арифметики от алгебры. В арифметическом выражении нет неизвестных элементов «2+4–1 = 5». Алгебра же дает возможность ставить неизвестный элемент куда угодно внутрь выражения «x+4–1 = 5», такие выражения называются уравнениями. Если мы введем в уравнение два неизвестных элемента, тогда мы получим функцию «y = x+4–1». Неизвестные элементы в функции принято называть переменными. В целом функция не имеет однозначного решения, их у нее целый спектр, который можно изобразить в виде графика. В большинстве случаев функции имеют бесконечное множество решений. Поэтому нельзя рассуждать о функциях, оперируя только числами, тут нужно вооружиться множествами. Свойства функций это как раз главное, что рассматривается математическим анализом.

Главным понятием в математическом анализе является понятие предела. Пределом называют некую величину, к которой стремится функция, но никак не может ее достичь. Если понятие функции еще можно определить, используя только числа, то объяснить что такое предел без привлечения множеств невозможно, потому что предел возникает только, когда мы изучаем не одно число, а множество чисел. Для примера возьмем те расстояния, на которые в нашей задаче черепаха всегда будет опережать Ахиллеса, это будет бесконечное упорядоченное множество чисел, начинающееся с единицы, и каждое последующее число в этом множестве вдвое меньше другого (1, 0.5, 0.25, 0.125 и т.д.). Такая последовательность имеет предел равный нулю, то есть каждое последующее число будет все меньше и меньше, стремясь к нулю, но на протяжении всей бесконечности этой последовательности ни одно число так и не станет полностью равным нулю. Можно сказать, что мы уже познакомились с пределом, когда чуть выше подробно разобрали, что последовательность отношений двух соседних чисел Фибоначчи стремиться к значению золотого сечения, а значит, оно является пределом этой последовательности. Наглядно продемонстрировать предел можно, если вспомнить гиперболу. Все величины у начала гиперболы стремятся к нулю, а в конце гиперболы все величины стремятся к бесконечности. Взять, к примеру, центр черной дыры это предел, к которому стремится искривление пространства-времени, в тоже время центр черной дыры недостижим, поскольку по мере приближения к этой точке искривление становится все сильнее и сильнее.

На основе предела в математическом анализе определяют понятие производной. Еще раз обратим внимание на задачу, в ней Ахиллес, догоняя черепаху, не только преодолевает все более короткие отрезки пути, но делает он это за все более короткие промежутки времени. Получается, что не только множество отрезков пути стремится к нулю, но множество промежутков времени тоже стремится к нулю. Так вот отношение любого отрезка пути к соответствующему промежутку времени легко можно вычислить, это отношение и называют производной. Грубо говоря, производная это скорость, с которой изменяется график. Задача про Ахиллеса и черепаху легко решается на интуитивном уровне, потому что скорости их движения постоянные. Однако задачи с переменными скоростями движения невозможно решить без привлечения производной. В задаче с переменной скоростью движения производная перестает быть постоянной величиной, она превращается в функцию. Поэтому даже если бы Ахиллес и Черепаха бежали бы с переменными скоростями, то изучив графики производных их движения, можно было бы однозначно установить, где и когда Ахиллес обгонит черепаху. Вообще решение задач при помощи производной называется дифференциальным исчислением. Оно было изобретено Ньютоном для математического описания своих трех знаменитых законов движения*. Главным требованием в дифференциальном исчислении является то, что график движения должен быть непрерывным. Непрерывность графика обеспечивается только тогда, когда функция может принимать иррациональные значения, следовательно, Ахиллес, догоняя черепаху, должен был пробежать отметку в квадратный корень из двух метров. Поэтому движение объектов всегда рассматривается, как явление, построенное на непрерывности, а не на дискретности. А если теория петлевой гравитации верна и пространство-время дискретно, то тогда не совсем понятно как в нем может порождаться непрерывное движение. Однако не стоит сразу обвинять теорию петлевой гравитации в неправдоподобности. Возможно то, как мы описываем движение, является лишь приближенной моделью того, что происходит в действительности.

Выходит, что изучение иррациональных чисел актуально и сегодня для решения самых фундаментальных загадок природы. Значит, касательно их реальности тоже есть еще много нерешенных вопросов. О реальности следующего класса чисел, порождаемых арифметическим корнем, на первый взгляд, можно однозначно сделать вывод, что они нереальны. Эти числа возникают, потому что корень это действие, которое не может дать однозначный результат. Например, квадратный корень из четырех может равняться двойке и минус двойке, причем оба утверждения верны, поскольку 2 × 2 = 4 и –2 × –2 = 4. С другой стороны, получается, что корень четной степени из отрицательных чисел не имеет смысла. Арифметика всегда отталкивается от числа «1», поэтому в предельном случае это правило формулируется так: квадратный корень из минус единицы не может ничему равняться, ибо нет такого числа, которое умноженное само на себя давало бы минус единицу. Это происходит, потому что отрицательные числа определяются как «ненастоящие» и умножение минуса на минус всегда дает плюс. Однако можно представить, что решение квадратного корня из отрицательной единицы существует, получившееся число называют мнимой единицей и обозначают знаком «i» (см. таб.10). Любые числа, которые включают в себя мнимые единицы, называют комплексными. Комплексные числа могут включать в себя только мнимую часть (2 × i или 2i – две мнимые единицы), а могут содержать как мнимую, так и реальную (2i + 3 – две мнимые единицы и тройка). Казалось бы, комплексные числа абсолютно лишены аналогов в реальности, потому что ничего нельзя измерить в мнимых единицах. Но оказывается, что комплексные числа обладают уникальными математически свойствами и помогают изучать многие явления нашей реальности, которые нельзя описать иначе. Любое комплексное число можно изобразить в координатной сетке, где мнимые единицы будут координатами по оси y, а реальные координаторами по оси x. Например, число 4i – 5, можно представить как точку на плоскости с координатами y = 4, а  x = –5. Получается, что комплексные числа превращают числовую прямую в числовую плоскость. Функции, построенные на комплексных числах, позволяют изучать такие явления, как например, искривления поверхностей. Так же их необходимо применять для некоторых расчетов в квантовой механике, и может, потому что в основе этой теории лежат комплексные числа, она так непостижима для нашего разума, непривыкшего к мнимым единицам.

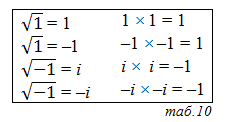
Кроме того комплексные числа замешаны в образовании хаотических структур из простейших элементов. Когда мы смотрим на форму ветвистого дерева или морозный узор на окнах, нас удивляет, каким образом могла появиться такая красота. Все ветки у дерева похожи друг на друга и в тоже время нет двух одинаковых. Не найдешь и двух одинаковых мазков в живописи природы на окне. Для объяснения этого нужно вспомнить хаос, который заставляет незначительные изменения в начальных условиях превращаться в далеко идущие последствия, а поведение систем делает непохожим на поведение их составляющих. Благодаря данному явлению вселенная сегодня такая сложная и многообразная, хотя и возникла из простых элементарных условий. Давайте разберемся, почему так происходит. Итак, как мы выяснили, что используя только множества, можно сделать математическое описание любых элементов реальности. Однако чаще пользуются не самими множествами, а соответствиями между ними, то есть функциями. Но даже если функция проста, график функции не всегда бывает так же прост как она сама. Иногда графики, построенные на простых функциях, проявляют признаки хаоса, и превращаться во фракталы. Фракталом называют сложную математическую фигуру, в которой встречаются самоподобные элементы, но, в то же время, ее структура остается хаотичной, непредсказуемой и неизмеримо сложной, хотя в основе фрактала лежит простая функция*. Причем наиболее сложные фракталы образуются, если в функции содержатся комплексные числа, поэтому считается, что комплексные числа играют большую роль в возникновении сложности из простоты.

Самый знаменитый фрактал – это множество Мандельброта, его функция содержит комплексные числа и записывается следующим образом: z₀=0; z_n+1=z_n²+c; c=x+iy. Если читатель и проходил высшую математику в институте, то он все равно вряд ли сможет построить такой график. Но это не беда, ведь даже у специалистов построение не получится, используй они только ручку и бумагу, потому что график получится настолько сложный, что его под силу будет воспроизвести только компьютерам (см. рис.41). Переводя взгляд с графика множества Мандельброта на функцию, по которой он строится, не верится, что в ее состав входит всего 20 математических символов. Поэтому у нас остается меньше поводов удивляться тому, что в основе вселенной тоже может лежать какая-нибудь простая математическая формула. Кто знает, может быть, весь наш мир – фрактал. Если это так, то все что нас окружает, является сложной математической структурой, притом в основе своей она проста и сложность ее только кажущаяся.

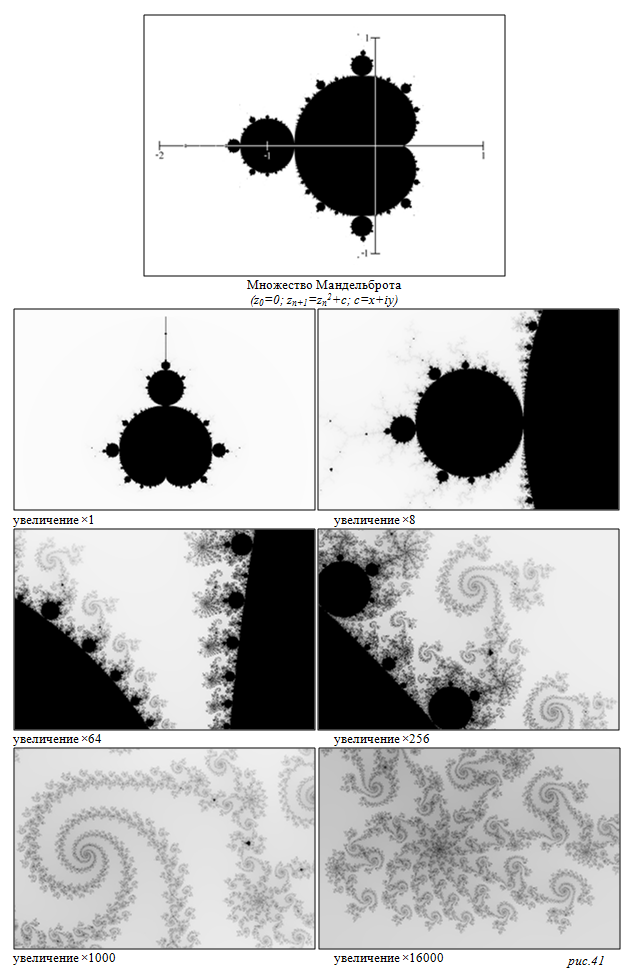
Комплексные числа, лежащие в основе таких формул, как множество Мандельброта, получают еще одно заслуженное отображение в природе. Однако на этом проявления комплексных чисел не заканчиваются. Другая их заслуга в том, что на фундаментальном уровне они связывают абстрактную алгебру с пространственной геометрией. Эта взаимосвязь выражена в формуле е^iπ = –1, которая носит имя Эйлера, российского математика швейцарского происхождения. В 1727 году считалось престижным для занятий наукой переехать из Швейцарии в Санкт-Петербург, где Эйлер и совершил все свои открытия. Чтобы разъяснить его формулу надо дать определение особым числам, которые в ней задействованы. С мнимой единицей мы уже знакомы, оба других числа не мнимые, а реальные, причем по своей природе не просто иррациональные, их еще называют трансцендентными*, потому что помимо того что их нельзя записать в виде дроби, они еще не могут выступать в качестве неизвестных элементов в уравнениях.

Число е приблизительно равно 2.718281… и имеет множество математических определений*, но чтобы наиболее понятно объяснить, чем оно особенно, нужно рассказать, как оно выводится на основе арифметики. Большинство арифметических структур возникает, когда мы пытаемся сделать что-то с одним и тем же числом. Если сложить число само с собой это все равно, что умножить его на два, а если умножить само на себя, значит возвести в квадрат. При вычитании числа из самого себя может получиться только ноль, при делении числа самого на себя может получиться только единица, логарифм по основанию того же числа тоже всегда даст единицу. Зато корень, другое обратное действие третьего уровня, не может дать в этом случае однозначного решения. Поэтому корень степени x из числа x будет иметь целый спектр решений в зависимости от использованного числа (см. таб.11).

Если последовательно использовать в выражении числа меньше e, результат будет убывать, но и если использовать числа больше чем e, результат тоже будет убывать (см. рис.42). Так происходит, потому что корень это вторичное обратное действие третьего уровня, первичным обратным действием третьего уровня считается логарифм*. Получается, что число е является порождением главного закона арифметики о том, что арифметические действия выше второго уровня теряют свойство коммунитативности и имеют второе обратное действие. Примечательно то, что число е используется не только в преобразованиях со степенью и ее обратными действиями, но оно естественным образом возникает и в арифметических действиях высших уровней.

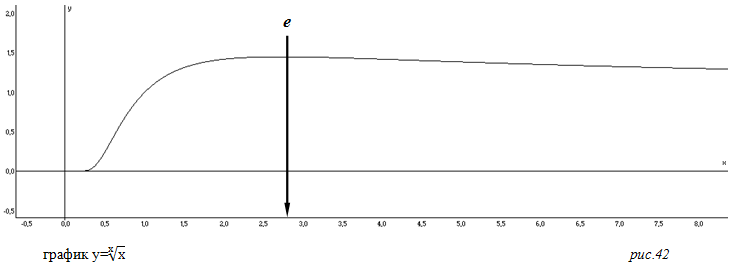
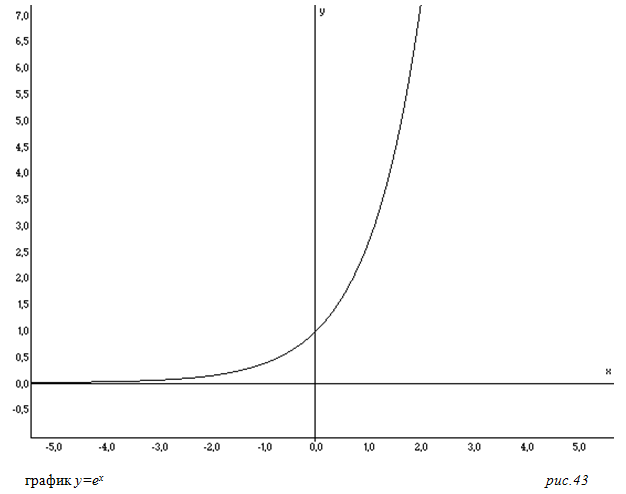
Eсть много других способов вывести это число, и оно появляется в разных разделах математики, но, наверное, самые важные функции e выполняет в дифференциальном исчислении. Число e используется для решения дифференциальных уравнений. Все это звучит как-то умно и сложно, подумает читатель, но если он хоть раз делал денежные вклады в банках, то он, скорее всего, даже в уме пытался решить дифференциальное уравнение, чтобы определить, сколько же процентов набежит в будущем. Естественно он не применял в своих вычислениях число e, значит, все его расчеты были приблизительными. Сейчас я покажу, как точно рассчитываются процентные ставки. Допустим, вкладчик сделал вклад n рублей, на срок m лет с процентной ставкой k, тогда изменение его суммы в банке будет рассчитываться по формуле n×e^mk. Это называется экспоненциальным ростом, ему подчиняются не только процентные ставки, но и много других явлений, будь то рост денежной инфляции, деление атомных ядер, размножение особей, деление клеток, ускорение развития технологий и даже расширение вселенной. В основе экспоненциального роста лежит экспонента – функция y=e^x (см. рис.43). Практическое применение экспоненты можно встретить практически в любой сфере. Для математического анализа эта функция важна одним своим уникальным свойством, если построить график скорости, с которой увеличивается экспонента, то этот график сам будет экспонентой. Иными словами экспонента является производной сама для себя, никакая другая функция таким свойством не обладает.

Многие могут заметить, что экспоненциальный рост по своим особенностям схож с гиперболическим ростом. Некоторые могут спросить, а какой из них сильнее. Но такая постановка вопроса неверна, потому что в реальных процессах каждый из них сопровождается коэффициентом, который и определяет интенсивность роста (y=e^kx – экспоненциальный рост, y=1/kx – гиперболический рост; k – коэффициент). В частности, процентная ставка как раз является коэффициентом. Например, в начале Большого взрыва во время космической инфляции вселенная расширялась экспоненциально, и коэффициент был очень большим, поэтому за мельчайшие доли секунд она расширилась сильнее, чем за все последующие годы расширения. Сегодня расширение вселенной подталкивает темная энергия, и оно тоже подчиняется экспоненциальному закону, только с гораздо меньшим коэффициентом. Принципиальное отличие обоих законов в том, что в гиперболическом росте одна величина уменьшается, другая возрастает, а в экспоненциальном росте обе величины увеличиваются. Поэтому гиперболический рост должен обращаться в бесконечность, когда его входящий параметр приближается к некой величине. Экспоненциальный рост, в свою очередь, такой величины не имеет. Объясню это различие на примере денежных вкладов. Какая бы не была у вас процентная ставка, пусть даже миллиард процентов, все равно число ваших средств в банке всегда будет конечным, хоть и очень, очень большим. С другой стороны, если бы рост вкладов по процентным ставкам подчинялся бы гиперболическому росту, то в определенный день количество ваших денег в банке стало бы бесконечным.

Некоторые космологи опасаются того, что расширение нашей вселенной может стать гиперболическим, такое явление может произойти, если темная энергия начнет увеличивать свою интенсивность. Это приведет к тому, что скорость расширения вселенной будет увеличиваться за все меньшие промежутки времени. Таким образом, раз одна величина (время) уменьшается, а другая (скорость) увеличивается, то экспоненциальный рост превращается в гиперболический, значит однажды скорость расширения вселенной станет бесконечной. Сегодня мало кто из ученых верит, что темная энергия сможет бесконечно усиливать свою интенсивность, ибо пока что она остается стабильной, поэтому, так называемого, Большого разрыва, скорее всего, не случится.

Вообще в природе часто так бывает, что экспоненциальный рост превращается в гиперболический. Гипербола является производной от обратной экспоненты (x=e^y), поэтому, когда в экспоненциальном росте одна величина начинает убывать, а другая продолжает расти, он превращается в гиперболический рост. Чтобы ваша сумма в банке стала расти гиперболически, проценты должны начисляться за все меньшие промежутки времени. Когда, приближаясь к некому значению, гиперболический рост обращается в бесконечность, это называют сингулярностью. Природа обычно избегает сингулярностей и когда гиперболический рост какого-либо явления начинает стремиться к бесконечности, происходит фазовый переход. То есть рост прекращается вообще и явление переходит из одной фазы в другую. Если какие-нибудь животные на земле начнут размножаться по гиперболической зависимости, это не значит, что через некоторое время их станет бесконечное количество, они просто вымрут от недостатка пищи. Так же гиперболическая процентная ставка не сделает вас бесконечно богатым, а просто разорит банк, в который вы вкладывались. Поэтому ученые и предполагают, что раз природа избегает сингулярностей, то гиперболический рост искривления пространства-времени внутри черной дыры должен производить некий фазовый переход, это значит, что либо пространство-время там полностью меняет свою структуру, либо рождается новая область пространства-времени (новая вселенная). Экстраполяция назад во времени к большому взрыву тоже происходит по гиперболической зависимости и сталкивает нас с сингулярностью, это намекает на то, что вселенная не могла быть бесконечно плотной, скорее всего, изначально пространство-время было в некоторой другой фазе, а большой взрыв был фазовым переходом из одного состояния в другое. Трансгуманисты, как и космологи, так же сталкиваются с сингулярностью, когда изучают развитие науки и техники. Ими было замечено, что сегодня прогресс начал двигаться по гиперболическому закону. Но это не значит, что в некий момент времени в будущем развитие науки и техники станет бесконечно быстрым, вероятно, как и в остальных случаях, здесь тоже случится фазовый переход. Как предполагают трансгуманисты, это будет переход из стадии разума в стадию сверхразума. Противники трансгуманизма иного мнения, они склонны приводить пример с размножением особей, и боятся, что гиперболический рост научно-технического прогресса закончится вымиранием человечества.

Какие все-таки удивительные проявления в природе могут иметь обычные математические зависимости, в основе которых лежит число e. Но в чисто физических формулах число е имеет еще более глубинный смысл, именно оно ответственно за однородность пространства-времени и закон сохранения энергии. Все уравнения, описывающие эти принципы, включают в себя экспоненту. Когда некий процесс в пространстве или во времени меняет систему отчета, или когда энергия перетекает из одной формы в другую, то с математической точки зрения происходят дифференциальные преобразования. Только одна функция при дифференциальных преобразованиях не меняется, это экспонента, потому что она сама себе производная. Поэтому если экспонента не входила бы в состав этих уравнений, то законы физики не соблюдались бы в любой точке пространства или в любом моменте времени, они бы постоянно изменялись. Так же не выполнялся бы закон сохранения энергии. На основе этого можно сделать вывод о законах в мультивселенной. Так как число e математической природы и в любой параллельной вселенной, вне зависимости от ее законов физики, будет иметь одно и то же значение, то во всех них должен выполняться закон сохранения энергии и закон однородности пространства-времени, и не существует такой вселенной, которая бы им не подчинялась. В принципе закон сохранения энергии итак не выполнялся бы без однородности пространства-времени. По-другому этот закон называют первым началом термодинамики. Вообще, все термодинамические начала принято считать не просто физическими законами, а, своего рода, конституцией физики. Второй закон термодинамики определяет характер протекания процессов, которые согласно ему должны стремиться к завершению, а неравновесная среда должна стремиться к однородности. Третий закон говорит о том, что абсолютный покой недостижим. Они, так же как и закон сохранения энергии должны соблюдаться во всех параллельных вселенных, если те существуют, ибо так повелевает математика. Однако внутри математических основ не удается найти указания, которые свидетельствовали бы о том, что такие параметры как интенсивность сил, свойства частиц и даже универсальные постоянные, вроде скорости света, тоже должны быть обязательными элементами реальности в параллельных вселенных. Следовательно, все это лишь местные постановления нашей вселенной, остается лишь найти принцип, по которому они были установлены.

Число Пи, тоже обладает важным физическим смыслом, который заключается в однородности вращения и пространственных направлений. Так же как число е отвечает за неизменность законов физики при передвижении, число Пи отвечает за неизменность законов физики при вращении. Это число замешено в описании колебательных процессов, а значит любые волновые явления, основаны на числе Пи, в том числе и вся квантовая механика. Во многих формулах статистики и теории вероятности оно тоже появляется естественным образом. Значение Пи в особом пояснении не нуждаются, это известное каждому школьнику, соотношение длины окружности с диаметром. В реальном мире проявлений числа Пи даже не сосчитать, однако, казалось бы, какое отношение к абстрактной арифметике может иметь это число, взятое из геометрии. Но так как число е имеет чисто алгебраическое определение, поэтому связь чисел е и Пи в формуле Эйлера (е^iπ = –1) говорит нам о том, что арифметика с геометрией неразрывно связанны. Тригонометрия – раздел математики, изучающий углы, в свою очередь, тоже имеет гораздо большее отношение к геометрии, чем к арифметике. Но если мы решим возвести число в степень равную мнимой единице, то исходя из формулы Эйлера, получим следующее выражение: aⁱ = cos(log_ea) + i∙sin(log_ea), где результат вычисляется по средствам тригонометрических функций (синуса и косинуса). Следовательно, тригонометрия тоже связана с арифметикой на фундаментальном уровне. Такое математическое единство обеспечивается благодаря числу е, числу Пи и комплексным числам. Это еще раз указывает на то, что абстрактные вещи кажущееся на первый взгляд мнимыми и ненастоящими могут находить отражение в реальности.

В реальном мире есть проявления и расширенных версий комплексных чисел, в которых может содержаться не одна мнимая единица, а сразу несколько. Способ введения новых мнимых единиц следующий: допустим, есть несколько чисел, которые, если возвести их в квадрат, дадут минус единицу, и, что самое главное, между собой эти числа не равны (i² = –1, j² = –1, i ≠ j). Такое математическое построение на первый взгляд уж точно должно быть лишено физического числа. Но подобно тому, как комплексные числа с одной мнимой единицей, дают возможность описывать точки на плоскости, так и гиперкомплексные числа представляют собой точки в пространстве, причем любой размерности, в зависимости от количества введенных мнимых единиц. Например, гиперкомплексные числа с тремя мнимыми единицами позволяют изобразить четыре измерения (к примеру, число 9+2i–7j+8k обозначает четыре координаты). Их называют кватернионами, и они широко используются в общей теории относительности для изучения искривленного пространства-времени. Однако у гиперкомплексных чисел есть и недостатки, увеличивая количество мнимых единиц в числе, мы отбираем у него арифметические свойства. Так, например, если в гиперкомплексном числе содержится две или более мнимых единицы, то оно теряет коммуникативность при умножении (от перестановки множителей результат меняется), а если в гиперкомплексном числе восемь или более мнимых единиц, то его уже нельзя делить. И, тем не менее, гиперкомплексные числа находят отображения в реальности, символизируя многомерность.

Что касается арифметических действий, уровень которых выше трех, то, как оказывается, на практике им почти нет применения. Эти высшие арифметические действия не встретить ни в одной физической формуле. Нельзя сказать, что они полностью бесполезны, во всяком случае, их существование доказывает, что математика гораздо богаче ее физических проявлений. Арифметические действия высших уровней получают по аналогии с тем, как вводится умножение и степень. Если сложить число с самим собой n-ное количество раз, это все равно, что умножить его на «n». Если число умножить с самим собой n-ное количество раз, значит возвести его в n-ную степень. Так вот выполнить арифметическое действие четвертого уровня, означает возвести число в равную этому числу степень «n» раз. Это преобразование называют тетрацией*. Записывается она таким образом «^ba». Так же как степень тетрация имеет два обратных действия, их называют суперкорень и суперлогарифм, новых типов чисел они не рождают, но ограничены в вычислении и в случае нерешаемости попросту теряют смысл. Да и сама тетрация выполняется только при использовании натуральных чисел, в большинстве остальных случаев она невычислима. Поскольку степень некоммунитативна, это приводит к тому, что тетрацию необходимо вычислять в определенном порядке: сверху вниз. Например, ³4 – это 4 в степени 4⁴, а не 4⁴ в степени 4 (³4 = 4²⁵⁶ ≠ 256⁴). Еще тетрация характеризуется тем, что даже если в ней использованы относительно небольшие числа, результат все равно будет огромен, поэтому ³4 ≈ 10¹⁵⁴ (число с 154 нулями). Становиться, понятно, почему у тетрации нет практических применений. Арифметические операции с уровнем выше четырех имеют схожие с тетрацией свойства. Результат вычисления для любых чисел, которые больше двойки, с каждым уровнем арифметической операции увеличивается все сильнее и сильнее, так что его становится уже невозможно выразить даже логарифмической записью.

Самое большое число, которое на сегодняшний день было задействовано в математике, это число Грэхема, оно использовалось для доказательств в комбинаторике. Это раздел математики, изучающий размещения, сочетания и перестановки элементов, в котором чаще всего приходится оперировать огромными числами. Мне хотелось бы показать читателю насколько велико число Грэхема, но его невозможно осознать без подготовки. Для начала возьмем число гугол, оно многим знакомо благодаря очень известной одноименной компании. Это единица с сотней нулей. В своей книге я использовал его только раз, когда объяснял, сколько лет проживут сверхмассивные черные дыры. Там же я упоминал, что столько нет даже элементарных частиц в пределах наблюдаемой вселенной, а если точнее их где-то в триллион раз меньше, чем гугол. В виде логарифмической записи оно выглядит так 10¹⁰⁰. Мы очень часто прибегали к логарифмической записи, когда путешествовали по природным масштабам, но иногда даже с ее помощью нельзя выразить большие математические числа. Теперь, когда я ознакомил читателя с тем, что такое уровень арифметического действия я могу объяснить что такое гипероператораная запись числа. Она будет нам просто необходима, чтобы понять масштаб числа Грэхема. Итак, что такое 10¹⁰⁰? Это число 10 подвергли операции 3-его уровня (возвели в степень) с показателем 100. Третий уровень арифметического действия в данном случае и есть гипероператор, а сама гипероператораная запись 10¹⁰⁰ будет выглядеть так 10[3]100. На примере гугла мне бы хотелось еще показать: почему комбинаторика обычно использует огромные числа. Для описания физических параметров вселенной найдется крайне мало величин сопоставимых с гуглом, но просчитывая вероятность в обычной карточной игре, можно легко столкнуться с гуглом. Например, есть такие виды карточных игр, в которых используется колода в 104 карты (две полных колоды 52+52). На вопрос, сколько вариантов последовательности карт будет в такой колоде после того как ее перемешать, ответ даст комбинаторика, и это будет что-то около 10¹⁶⁵, что на 65 порядков превышает гугол.

Что ж идем дальше. Ради забавы математики придумали гуголплекс, это число представляет собой единицу с гуглом нулей. Записать гуголплекс обычным способом уже невозможно, потому что даже если бы мы смогли рисовать нули на элементарных частицах, нам все равно бы не хватило их во всей наблюдаемой вселенной. Даже логарифмическая запись (10 в степень гугол) смотрелась бы слишком громоздко. Поэтому для записи таких чисел, иногда используют степенную башню, в случае с гуголплеком, она будет выглядеть как 10 в степени 10 в степени 100, на основе чего можно вывести и гипероператорную запись 10[3](10[3]100). А вот чтобы понять насколько число 10[4]10 больше чем гуголплекс, следует посмотреть на рис.44, потому что для его записи без степенной башни вообще не обойтись.

Как я и говорил, тетрация приводит к огромным, почти невообразимым числам. Но если мы будем увеличивать уровень арифметического действия, то и уровень невообразимости, если так можно выразиться, тоже будет расти. По аналогии 10[4]10 = 10[5]2, а 10[5]10 = 10[6]2. Причем для того чтобы выразить 10[5]10 нам не поможет даже не степенная башня, ибо ее размер сам по себе станет огромным, поэтому придется записывать его в виде тетрационной башни. В свою очередь число 10[6]10 уже нельзя записать никаким другим способом, кроме как с помощью гипероператора. Если кто-то уже перестал осознавать величие таких чисел, то спешу его огорчить тем, что на самом деле мы только подобрались к пониманию числа Грэхема. На начальном этапе создания числа Грэхема нам потребуется число 3[6]3, которое хотя и меньше чем 10[6]10, но все равно мы не сможем записать его, ни в виде степенной, ни в виде тетрационной башни, настолько оно большое. Причем число 3[6]3 это только первый этап в построении числа Грэхема из 64-ех! Второй этап создания выглядит так: 3[3[6]3]3. И что же это значит? Для первого этапа мы с числом 3 производили арифметическую операцию 6-го уровня, что в виде гипероператорной записи выглядит так 3[6]3, а на втором этапе сам уровень арифметической операции стал 3[6]3, вот и получается 3[3[6]3]3. Соответственно третий этап: 3[3[3[6]3]3]3. И так далее. Всего 64 этапа! Очевидно, что даже в виде гипероператорной записи это число будет выглядеть очень громоздко, но, увы, более лаконичного вида записи в математике не придумано. Не расстраивайтесь, если вам не удалось с первого раза осознать масштаб числа Грехема, у меня это тоже не сразу получилось*.

Все-таки какие бы числа не получались в результате арифметических сверхопераций, они будут меньше бесконечности. Даже число Грэхема ничто по сравнению с бесконечностью. Но ранее упомянутая, теория множеств умеет производить арифметические действия даже над бесконечностью и уверяет, что в природе есть вещи бóльшие, чем бесконечность. С этим надо разобраться и выяснить какова математическая природа бесконечности. У многих мог возникнуть вопрос, когда мы рассуждали о возможности того, что вселенная бесконечна. Звучит он следующим образом: как наша вселенная может быть бесконечной и при этом расширяться. Каким образом бесконечная вселенная могла быть меньших размеров? Чтобы понять это, нужно обратиться к свойствам бесконечности. Прежде всего, для себя нужно усвоить, что с математической точки зрения бесконечность – это не число, а множество, включающее в себя неисчислимую совокупность элементов. В связи с этим известно много загадок, кажущихся на первый взгляд парадоксальными. Помимо теоремы о бесконечных обезьянах, есть другая занимательная задачка, связанная с бесконечностью, ее называют отель Гильберта, в честь математика, изучавшего свойства бесконечности.

По условиям задачи мы имеем отель с бесконечным количеством номеров, в которых живет бесконечное количество постояльцев. Вопрос, как заселить в отель еще одного человека? Ответ, звучит так: нужно обратиться к постояльцу из номера «1» с  просьбой о переселении в следующий по счету номер, и чтобы он попросил о том же постояльца из того номера, передав, что администрация отеля приносит глубочайшие извинения за неудобства. В итоге все постояльцы все равно останутся с номерами, а у нас появиться одно свободное место.

Не нужно быть выдающимся математиком, чтобы осознать: сколько не прибавляй к бесконечности, она все равно останется бесконечностью. То же самое с вычитанием, умножением и делением – какое бы действие мы не применили, бесконечность останется непоколебимой. Даже если мы сложим или умножим бесконечность саму с собой, ничего не изменится. Другое дело если попытаться вычесть бесконечность из бесконечности, по идее должен получиться «0», но если рассмотреть эту ситуацию подробнее, то все оказывается не так просто. Допустим, если мы возьмем постояльцев из четных номеров и выселим их из отеля. Их число будет бесконечным, как собственно и число постояльцев оставшихся в нечетных номерах, следовательно ∞ – ∞ = ∞. Наши действия с выселением из четных номеров это все равно, что разделить бесконечность на два, а как мы выяснили бесконечность, деленная на любое число, дает бесконечность. Но что если разделить бесконечность саму на себя, получиться ли в соответствии с правилами арифметики «1»? В принципе это тоже кажется оправданным. Имея бесконечное число постояльцев, и расселяя их в отель с бесконечным числом номеров, мы должны добиться того, что каждому постояльцу достается по одному номеру. Но как бы, ни так, ведь мы можем заселять постояльцев через 4 номера, оставляя их пустыми, так что на каждого постояльца придется по пять номеров. Можем вообще каждому заселяющемуся отдавать по 10 или 50 номеров, да хоть по ∞ номеров в идеале, все равно в результате такого расточительства гостиничной собственности все постояльцы будут заселены, следовательно ∞/∞ = ∞*.

Возведение бесконечности в степень – это тоже, что перемножить ее между собой несколько раз. Поэтому, в какую бы степень мы не возвели бесконечность, это не должно ничего изменить в сложившейся ситуации. Однако вот такое выражение ∞^∞ кардинально меняет результат. Чтобы понять чему равно ∞^∞, нужно подробнее обсудить природу бесконечности. Для начала я хочу спросить читателя, каким образом, он вообще представляет себе бесконечность. Некоторые приведут бесконечный ряд каких-то предметов, а некоторые приведут бесконечную линию. И те и другие правы, но рассмотрим детальнее случай с бесконечной линией. Если мы будем измерять бесконечную линию в отрезках, то она в любом случае будет бесконечной, в независимости от длины этих отрезков. Попробуем измерить ее в безразмерных точках, в итоге опять получим бесконечность. Но есть один нюанс, бесконечность точек на бесконечной линии будет больше бесконечности отрезков на той же линии. Данное высказывание было доказано Георгом Кантором. В его время математики посчитали это доказательство научным шарлатанством и не прияли Кантора всерьез. Кстати это именно он впервые определил понятие множества, которое сегодня считается самым фундаментальным понятием в математике, кроме того он фактически и являлся создателем теории множеств. В его деятельности, как математика была одна проблема, он опередил свое время. Постоянная агрессивная критика его работ и безуспешные попытки установить соответствия между различными бесконечностями в своей теории, привели к тому, что Георг Кантор сошел с ума. Задача, над которой он работал, остается нерешенной, и по сей день. Сам Кантор, уже находясь в состоянии маниакально-депрессивного психоза, утверждал, что решил эту задачу, связавшись при этом с высшими силами, но он не может объяснить решения, потому что не может выразить лежащую в ней и открывшуюся ему «философию».

Так что же заставило Кантора объявить, что существуют явления больше бесконечности. Главную роль в его теории играют иррациональные числа. Когда мы делим бесконечную линию на отрезки, то получаем бесконечность дискретных элементов, которые можно считать. Естественно, если мы попытается их сосчитать, то нам не встретится отрезка под номером квадратный корень из двух. Однако если разбить бесконечную линию на безразмерные точки, то где-то на линии можно поставить точку равную отметке в квадратный корень из двух. Пока что мы рассматривали бесконечности только такого типа «1,2,3 и так далее», но ведь последовательность «0.5, 0.25, 0.125 и так далее» тоже является бесконечностью. Это означает, что даже между нулем и единицей уместится бесконечное количество дробных чисел. В задаче про Ахиллеса все эти дробные числа символизируют пробегаемые им отрезки пути, которые хоть и стремятся к нулю, но все же они рациональны и поддаются счету. Тем не менее, Ахиллес таки пробегает отметку равную квадратному корню из двух, потому что его движение непрерывно. Теперь вспомним, что гипотенузу равностороннего прямоугольного треугольника невозможно выразить теми же единицами что и катеты, потому что она по отношении к ним иррациональное число. Сколько бы мы не увеличивали стороны треугольника, гипотенуза всегда останется иррациональной. Здесь похожая ситуация сколько бы мы не делили участки пути, иррационального числа мы так и не получим. Значит, сколь малые величины дробных чисел мы бы себе не представили, где-то между ними всегда будут находиться иррациональные числа (см. рис.44).

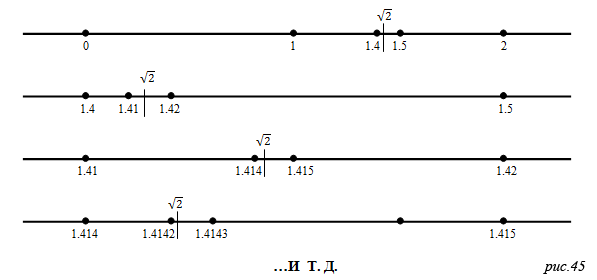
Если бесконечность целых чисел можно сопоставить бесконечности дробных чисел, потому что каждый элемент в бесконечном множестве «1,2,3 и так далее», сопоставим с элементом из бесконечного множества «0.5, 0.25, 0.125 и так далее», то иррациональные числа нельзя сопоставить с ни с целыми, ни с дробными. Раз на линии они всегда находятся где-то между, то точек, соответствующим иррациональным числам, всегда будет больше. Поэтому бесконечность рациональных чисел будет меньше бесконечности иррациональных чисел. Первую бесконечность обозначим индексом «1», а вторую индексом «2» и заключим, что ∞₁ < ∞₂. Данные индексы называют мощностью бесконечности*. Их математическое соответствие 2^∞ = (n>2)^∞ = ∞^∞ = ∞₂ говорит о том, что возведение в бесконечную степень, приводит к увеличению мощности бесконечности.

Итак, бесконечности бывают разных мощностей, но что это значит для реального, а не математического мира. Неисчислимое количество отрезков на линии это бесконечность первой мощности, потому что это бесконечность дискретных элементов. В свою очередь неисчислимое количество точек на линии это бесконечность второй мощности, потому что она непрерывна. И если вся физика нашего мироздания не дискретна до самых основ, если пространство-время не состоит из отдельных элементов, тогда наш континуум это больше чем просто бесконечность. Если вам тяжело было представить обычную бесконечность, то попробуйте тогда вообразить бесконечность второй мощности, которая больше первой, и ваш разум окончательно отключиться. Вообще долго рассуждать на такие темы не рекомендуется, стоит только вспомнить об участи Кантора*.

И все же если читатель крепок рассудком и готов еще немного поразмышлять о бесконечностях, тогда стоит разобраться какие еще отображения могут встречаться у бесконечностей разных типов. Мы выяснили, что бесконечность первой мощности применима только к дискретным элементам, которые поддаются счету. Поэтому бесконечность натуральных и дробных чисел имеет первую мощность, ибо их в отличие от иррациональных чисел можно считать. Бесконечность второй мощности относится к тому, что уже не поддается счету, она применяется для описания точек на линии, или линий на плоскости. Да и вообще ее можно применять, если речь идет о количестве точек в пространстве любой размерности или о количестве прямолинейных элементов, размерность которых меньше размерности содержащего их пространства. В арифметике бесконечность второй мощности это не только совокупность всех иррациональных чисел, но она так же сопоставима с совокупностью всех комплексных чисел и с совокупностью всех видов гиперкомплексных чисел. Значит, если мы соберем в кучу, все типы чисел, которые нам известны, то получим лишь бесконечность второй мощности. Бесконечность третьей мощности это совокупность всех возможных функций, она тоже имеет наглядную интерпретацию. К ней относят количество кривых на плоскости или в более общем случае количество криволинейных элементов в пространстве любой размерности. Однако мы не можем придумать числа, совокупность которых составляла бы бесконечность третьей мощности, а это значит, что для того чтобы описать кривые на плоскости нам просто не хватит чисел. Здесь мы окончательно дошли до границы применения чисел. Раздел математики, изучающей непрерывность криволинейных элементов в пространстве, называется топологией, и он не нуждается в числах, там оперируют только множествами*. Что касается бесконечности четвертой мощности, то она уже не имеет соответствий, даже если попытаться описать с помощью нее всевозможные абстрактные понятия. То есть, в математике нет таких элементов, совокупность которых составляла бы бесконечность четвертой мощности.

Получается, что ∞₄ не имеет никаких аналогий не только в реальности, но и в абстракции. Можно сказать, что бесконечности выше третьей мощности это всем абстракциям абстракции. Числа, которые обозначают мощность бесконечностей, называют кардинальными. Но ведь если мы будем считать кардинальные числа, то можем в итоге получить «∞₁, ∞₂, ∞₃, ∞₄, ∞₅ … ∞_∞». Как такое вообще понимать? Да, скорее всего никак, это просто математическая забава. Тогда продолжим эти забавы и попробуем применить к бесконечности тетрацию. Запишем такое выражение «^∞∞» – его результатом как раз и будет ∞_∞. Если мы применим арифметические действия высших уровней, мы можем получить еще большие сущности, которые уже трудно записать принятой нами записью. Тогда вопрос нужно поставить таким образом, есть ли предел у этой последовательности супербесконечностей.

Раньше математики предполагали, что существует, так называмая, абсолютная бесконечность, больше которой ничего не существует и существовать не может, ибо она всеобъелющая. Но с ней связана одна важная проблема, осознание которой ставит вопрос о границах самого познания. Итак, получается, что теория множеств теоретически допускает существование абсолютной бесконечности, на языке теории ее называют множеством всех множеств. Первым существование парадокса заметил, еще сам Кантор и отметил, что существование такого абсолютного множества делает теорию множеств противоречивой. В историю это противоречие вошло, как парадокс Рассела, в честь математика который доказал, что теория множеств действительно допускает существование множества всех множеств. Если не прибегать к математическому аппарату, то парадокс на самом деле весьма прост, если существует множество всех множеств, то куда входит это множество. Для наглядности создано множество интерпретаций. Одна из них возможно даже многим знакома и звучит так: придворному брадобрею царь приказал побрить во дворце всякого, кто сам не бреется, и не брить того, кто сам бреется. Кто же тогда побреет брадобрея? Еще одна менее известная, но более наглядная интерпретация описывает некое государство, в котором был издан указ о том, что мэры городов не имеют право жить в своих городах, а должны жить в специальном городе мэров, в котором тоже должен быть избран мэр. Вопрос, а где он должен жить? Получается, что теория множеств говорит, что абсолютная бесконечность должна существовать и тут же говорит, что она не может существовать.

К тому, откуда берется это противоречие и почему оно так важно, мы вернемся немного позже, а сейчас предлагаю выяснить, как вообще в математике могут существовать такие структуры, которые невозможно представить даже абстрактно. Материалисты уверены, что все это фантазии, не имеющие даже косвенного отношения к реальности. Но такая точка зрения не может быть верной, потому что эти математические структуры не придумывают, а открывают, так же, как открывали законы термодинамики и принципы квантовой механики. Попробуйте ответить мне, где были все вышеприведенные математические конструкции до того как я рассказал их вам. Согласитесь, что если теорему Пифагора открыл бы кто-нибудь другой, ведь не была бы она от этого другого вида. Часто бывают случаи, когда теоремы открывают независимо несколько математиков, поэтому эти абстракции нельзя называть выдумкой. Вопросом о том, где существовали математические структуры, до момента их открытия человеком, был озадачен еще Платон. Он предположил, что наряду с реальным миром должен существовать мир чистой абстракции, который теперь называют платоновским миром.

С другой стороны разница между физической вселенной и математической конструкцией, которая ее описывает, может существовать только в человеческом разуме. Возвращаясь к популярной ныне гипотезе о том, что в основе физики лежит информация, а наш мир это лишь компьютерная модель, немного поразмыслив, мы все же придем к выводу, что эта модель и есть реальность, а значит, абсолютно все в ней является не более чем математическим алгоритмом. Разница возникает в нашем сознании потому так устроено наше познание мира, а свой разум мы привыкли считать отдельным ментальным миром. Взаимосвязь платоновского, реального и ментального мира довольно интересно была изображена физиком и математиком, специалистом по черным дырам Р. Пенроузом. Его схема выглядит следующим образом: наш реальный физический мир происходит из маленькой части мира математики, остальные математические модели лишь абстракции не воплощенные в реальность. Из физического мира какая-то маленькая часть, которую мы без лишней скромности называем человеком, может думать. Остальная материя воплощена в мертвых планетах, звездах, галактиках, а может даже в целых мертвых вселенных. Люди способные думать создают, таким образом, собственный ментальный мир, называемый разумом. Мы склоны думать о разных вещах, а абстрактный математический мир, это лишь маленькая часть того, что рождается в наших головах. Цепь замкнулась!

Вопрос о том, что первично в этой цепи будоражит умы философов с древности. В народе он больше известен как загадке-прибаутке о курице и яйце. Сегодня мы знаем, что Большой Взрыв создал нашу вселенную, частицы и силы. Законы физики удачно сложились и частицы в нашей вселенной под воздействием сил образовали звезды. Звезды породили планеты, планеты живых существ. Существа развились и стали обладать разумом. Разум помог им понять, что они произошли от живых существ, живших раньше, те в свою очередь зародились на планете согреваемой светом звезды. И вот совсем недавно разум, понял, что звезды и планеты родились на основе законов физики с помощью сил из частиц, созданных Большим взрывом. Поэтому загадку мы можно перефразировать так: что было раньше разум или Большой взрыв, ведь до появления разума сама природа, скажем в лице динозавров, ничего о Большом взрыве то и не знала.

Ученые без проблем разрешат этот парадокс, объявив вторую часть рассуждений психологизмом. Психологизм – это философское течение, которое утверждает, что если бы не было разума, не было бы и вселенной, поскольку некому было бы понять, что есть вселенная. Основу этому течению заложил, вероятно, еще сам Сократ. В наши дни психологизм вновь начал набирать популярность, особенно после того когда ученые стали подробно разбирать следствия квантовой механики. Например, эксперимент квантовый ластик, который позволяет переписать прошлое светового луча, или эффект коллапса волны вероятности, который говорит о том, что частицы существуют лишь когда их наблюдают – все это приводят в поддержку психологизма. Из последних открытий в физике, сторонники психологизма чаще всего ссылаются на голографический принцип, с позиции которого черные дыры уже не физические объекты, а абстрактные компьютеры, и такое же предположение можно сделать в отношении всей Вселенной. Тем не менее, все это не может доказать правоту психологизма. Более того правота психологизма вообще не может быть доказана, потому что согласно психологизму научные доказательства бессмысленны. Ведь если окружающая нас Вселенная это порождение нашего разума, то и объяснение ее поведения так же должно рождаться только в нашем разуме. Психологизм в итоге должен приводить к заключению, что если разум единственно реально существующая вещь, то все остальные физические объекты, в том числе другие люди лишь иллюзии, создаваемые им. Именно поэтому идеи Психологизма не могут рассматриваться научными методами.

В противовес психологизму выступает реализм. С точки зрения реализма: мир вполне может существовать и без нас, потому что до зарождения разума должны были сформироваться условия к его существованию. Родоначальником этой точки зрения был Платон, который, между прочим, являлся учеником Сократа. И вот спор между учеником и учителем идет уже на протяжении тысячелетий. Сегодня наше рациональное мышление заставляет нас согласиться с Платоном. По его учению человек это лишь способ вселенной думать о самой себе, не более. Но если мы отвергаем психологизм и находимся на стороне Платона, тогда мы вынуждены признать, что существуют три ипостаси бытия: реальное, абстрактное и непостижимое. Например, реальным является физическое явление, абстрактным – теория, которая объясняет это явление, а непостижимым – аксиома, от которой отталкивается теория. Поэтому с позиции реализма вопрос о том, что первично в цепи «абстрактное - физическое - ментальное» вообще не имеет смысла, потому что все это одинаково реально.

Мы с вами на протяжении всей книги рассматривали реальное, в этой последней главе затронули абстрактное, но практически не касались непостижимого. Однако ученые уже давно склоняются к тому, что непостижимое действительно существует. Ярким тому примером служит теорема о неполноте математики. Ее создал Гедель, математик, который первый указал на то, что общая теория относительности разрешает путешествия во времени, так вот он же доказал непостижимость математических аксиом. Согласно этой теореме фундаментальные математические основы не могут быть объяснены, или доказаны, потому что иначе им пришлось бы опираться на еще более фундаментальные. Грубо говоря, теорема о неполноте означает, что математические аксиомы не могут сами себя объяснить, а значит, они просто есть. Почему аксиомы есть; и почему они такие, какие есть – это, в принципе, непостижимо.

Чтобы наглядно продемонстрировать теорему о неполноте, нужно рассказать про один парадокс, связанный с самой логикой. Вообще термин «парадокс» обозначает, нечто, не согласующиеся с логическим суждением. Но оказывается, что логическое суждение, наш главный инструмент в познании мира, само по себе парадоксально. Перед тем как перейти к описанию парадокса нужно сказать, что логика может быть описана математически. Она изучается разделом, называемым алгебра логики. Этот раздел в основе своей оперирует лишь только двумя цифрами: 0 – нет, 1 – да; и тремя логическими операциями: И, ИЛИ, НЕ (эти операции в основе своей те же, что и рассмотренные нами ранее базовые операции из теории множеств: объединение, пересечение и отрицание). Раз логика может быть описана математически, то и теорема Геделя о неполноте математики, может быть объяснена в данном парадоксе. Это противоречие первыми опять же заметили древние греки и назвали его «парадоксом лжеца», а заключается он всего в двух словах: «Я лгу». Понятно, что оное выражение не может быть ложью, иначе бы я говорил правду. Но и правдой оно быть не может, потому что я утверждаю что соврал. Это выражение абсурдно, его нельзя ни доказать, ни опровергнуть. Компьютерное вычисление, да собственно и вся информатика, целиком и полностью построена на алгебре логики, поэтому данную фразу легко сформулировать компьютерным языком и ввести в текст программы, естественно компьютер при этом зависнет. Все потому, что эта фраза пытается объяснить саму себя. Поэтому и математические аксиомы не могут быть объяснены без привлечения новых аксиом.

В самом начале главы мы выяснили, что любой раздел математики и алгебра логики в том числе, происходят из теории множеств, поэтому наиболее фундаментальными в математике, считаются аксиомы теории множеств. Так вот все они проявляют те качества, о которых говорил Гедель, то есть не способны объяснить сами себя. Примером этому служит как раз тот самый парадокс Рассела, который с одной стороны допускает существование абсолютного множества, с другой стороны говорит, что это невозможно, а вся причина опять же в том, что тут теория пытается объяснить сама себя. Отсюда следует вывод, что самые фундаментальные аксиомы математики в принципе непостижимы, такова их природа. Таким образом, если основа платоновского мира непостижима, то и невозможно понять, как математика рождается в нашем разуме.

С другой стороны происхождение физического мира тоже может находиться в зоне непостижимости. Проблема познания окружающего мира заключается даже не в том, что наша логика не способна логически объяснит саму себя, главная сложность была подмечена Кантом в его «Критике чистого разума» и заключается в том, что наш разум не может быть «чистым». Все потому, что он развивался в ограниченной среде срединных размеров. В этой среде нет места микроскопическим квантовым неопределенностям, нет места скоростям, при которых время начинает замедляться, нет места и многому другому, все это ставит ограничения. Поэтому нам трудно понимать квантовую механику и теорию относительности, хотя с математической точки зрения они выглядят естественными. Мы познаем мир при помощи пяти органов чувств или при помощи инструментов, сделанных из того же материала, что и изучаемый ими мир. Наш разум продукт эволюции, он имеет корни в физическом мире, и его нельзя рассматривать отдельно. Так можем ли мы говорить, что правильно воспринимаем действительность. Чтобы осознать истину нужно посмотреть на наш физический мир извне, но это невозможно сделать, потому что мы всегда будем находиться внутри него. Следовательно, мир никогда не будет познан с абсолютной точностью – такое заключение сделал Кант.

Люди, будучи трехмерными существами, не могут визуально представить четырехмерный объект, но его можно описать математически. Существует множество других объектов, которые  вообще невозможны в реальности, но могут быть описаны математикой. Но все ли может объяснить наш разум с помощью математики, особенно учитывая то, что математика не способна объяснить свои аксиомы. Что если мы никогда не сможем даже математически понять сущность, из которой происходит пространство-время и все остальное. Ведь муравей не обладает разумом и никогда не сможет рассуждать на тему квантовой механики и элементарных частиц. Имеет ли и разум границы применимости?

Даже если мы ответим на весь перечень вопросов, которые сегодня вменяют, так называемой «теории всего», то появятся новые. Так может продолжаться до тех пор, пока мы не столкнемся с такой же непостижимостью, как в математике, когда теория не сможет объяснить все свои аспекты. Например, современные исследования в теории струн заставляют некоторых физиков сделать вывод, что если теория струн верна, то, скорее всего, она не может быть единой теорией. Вероятно это совокупность теорий, каждая из которых может прояснить некоторую часть другой, но они как аксиомы в математике, не могут быть сведении к единым корням и объяснить сами себя. Может быть и такое, что квантовая теория гравитации, чем бы она ни являлась, теорией струн ли, петлевой гравитацией ли, единой теорией или совокупностью связанных теорий, или чем-то совершенно иным, она не станет последней инстанцией физических явлений. Что если мы обнаружим, что между физикой и абстрактной математикой может оказаться бесконечная череда теорий.

Но допустим, что эта единая физическая теория существует, допустим, разум человека все-таки сможет ее постичь, даже если этих теорий несколько и все они описывают наш физический мир. Тогда мы сможем заявить, что такая-то, или такие-то математические конструкции воплощают наш физический мир, но тут же назреет вопрос почему только она (или они) наделены физическим воплощением. Так или иначе, в этом случае мы придем к выводу, что может существовать не только несколько математических конструкций, которые воплощают физические миры идентичные нашему, но и есть бессчетное количество математических конструкций, которые потенциально могут воплощать иные физические миры. С одной стороны мы знаем, что наш физический мир, чем бы он ни был, единой вселенной или мультивселенной, и каким бы он ни был конечным или бесконечным, так или иначе он существует, но это не может быть доказательством того что другие физические миры потенциально порождаемые другими математическими конструкциями выдумки. Ведь мы пришли к выводу, что платоновский мир, который включает в себя все возможные абстракции и математические структуры существует, а раз так значит и физические миры, потенциально воплощаемые иными физическими конструкциями должны существовать. Вопросы наподобие, где они, и когда они, по отношению к ним так же бессмысленны, как и к объектам платоновского мира. Нас должно волновать другое, почему мы с вами находимся именно в этом физическом мире, если потенциально возможны и другие.  В данном вопросе антропный принцип не применим, ведь если с параллельными вселенными все понятно, и наше существование возможно лишь в той вселенной, в которой физические законы его допускают, то математических конструкций настолько много и они настолько разные, что могут воплощать какие угодно физические миры. Все согласятся с тем, что сложных математических конструкций больше чем простых, а если исходить из того, что их число бесконечно (и неважно какой мощности эта бесконечность), то вопрос, почему нашему миру досталась именно такая математическая конструкция, которую в принципе способен осознать человеческий разум тоже останется без ответа. Следовательно, теория всего, если она будет открыта, не сможет объяснить, почему она именно такая, какая есть.

Пенроуз предполагает, что так же как непостижимы основы платоновского мира математики, непостижимыми могут оказаться основы физического мира, и даже мира ментального. Таким образом, в его схеме непостижимости расположились в тех местах, где один мир происходит из другого. Согласно такой концепции, мы никогда не сможем понять, как математика рождается в наших головах, как физический мир рождается из математики, и как наш разум возник из физического мира. По поводу непостижимости основ математики сегодня согласны все, но что касается непостижимости основ физики, тут нет единого мнения. Множество ученых уверено в том, что «теория всего» все-таки должна существовать, хотя и соглашаются, что она может быть не сводима к единым корням, а напоминать связанную систему математических аксиом, неспособных друг друга объяснить.

В принципе физика уже давно, начиная с открытия квантовой механики, оперирует абстракциями как реальными объектами, но пока они остаются лишь моделями поведения, и мы не можем сказать, что основы нашего мира – есть абстракции. Однако, например, с точки зрения общей теории относительности есть места, в которых физика переходит в чистую абстракцию, они же, кстати, считаются главной ее проблемой – это начало большого взрыва и сердце черных дыр, где нет привычного для нас времени и пространства. Вопрос «Что там есть?» в рамках человеческой логики, применительно к этим явлениям, не имеет смысла. «Есть (быть, существовать)» - все это глаголы, обозначающие действие, а значит подразумевающие длительность и без понятия времени они немыслимы. «Там» - местоимение обозначающее местоположение в пространстве, а значит в условиях отсутствия пространства неприменимо. Остается только «Что?» Пытаясь описать словами данные явления, мы запутаемся в логических парадоксах. Однако по отношению к математическим объектам мы без всяких логических проблем можем сказать, что абстракции существуют вне времени и пространства, хотя понятие «существуют» и здесь звучит не совсем корректно, тем не менее, никак по-другому мы изъясниться не можем. С математической точки зрения центр черных дыр и начало большого взрыва описываются вполне естественным математическим термином – сингулярностью. Тем не менее, мы не можем сказать, где та грань, за которой заканчивается математическая абстракция и начинается физический мир. В этом примере как раз и прослеживается та непостижимость, что заключается в происхождении физического мира из мира математической абстракции.

Последний пункт в выводах Пенроуза о непостижимости происхождения разума из физического мира наиболее спорный, особенно для науки в целом, потому что в таком случае противники научной картины мира начнут говорить, что раз наука неспособна объяснить как возникает разум, значит, это доказывает существование души и бога. Ничего такого в действительности это не доказывает. Непостижимость по своей природе вообще ничего доказывать не может и уж тем более существование потусторонней силы. Кроме того разум нельзя рассматривать отдельно от понятия жизни, а как мы выяснили, происхождение и эволюция жизни тесно связаны с хаосом, который сам по себе не поддается объяснению. Сложность разума может быть необъяснимой так же как фрактал, который на основе простого уравнения превращается в сложнейшую фигуру, но никто не может объяснить, чем обусловлена эта сложность.

Некоторые считают, что если базовые основы разума не могут быть постижимы, то это накладывает ограничения на создание искусственного разума. В действительности это не так, искусственный разум можно создать, по принципу моделирования, даже не зная основ. Компьютер тоже не понимает в чем основа сложности фрактала, однако шаг за шагом моделирует его. Ни один компьютер не построит абсолютную модель фрактала, однако с легкостью смоделирует любой его участок, и вам будет казаться, что вы наблюдаете за целостной структурой. Таким же образом, сделав грубую модель человеческого разума, ее можно совершенствовать до тех пор, пока человек пообщавшись с этой моделью, при этом, не зная, что он говорил с машиной, не отличит ее от другого человека. Такой эксперимент называют тестом Тьюринга, и если компьютерная программа, моделирующая человеческий разум, сможет раз за разом проходить этот тест, тогда вполне правомерно считать ее искусственным разумом. Тут встает другая задача, именуемая проблемой формализации, она заключается в том, что мы пока не знаем, как смоделировать некоторые способности человеческого разума. Возможно, в будущем решить эту проблему нам помогут квантовые компьютеры.

Непостижимость научным языком называют трансцендентностью, и это не что-то паранормальное, а естественное явление, которое отличается лишь тем, что по своей природе не может быть объяснено. Трансцендентность в чистом виде это научные константы, аксиомы, постулаты, а отнюдь не то, чем увлекаются эзотерики. Наглядный пример – значение чисел e и Пи. Никто не даст вам ответ на вопрос, почему число Пи равно 3.14..., а число e равно 2.71…  Их не зря назвали трансцендентным, потому что нет возможности объяснить их числовые значения. Конечно, как и любое иррациональное число, оба можно расписать в виде бесконечных рядов (см. таб.12), но вопрос все равно останется без ответа. Попробуйте объяснить, почему эти бесконечные ряды именно такого, а не другого вида. Физики-теоретики стремятся в своих теориях избавиться от лишних необъяснимых констант, выводя их из чего-то более фундаментального, но от математических констант, таких как e и Пи, им не избавится никогда. Это трансцендентность, которая всегда будет присутствовать в физических теориях.

Однако, как уже говорилось, разум может быть не последней стадией эволюции. Есть надежда на то, что постичь непостижимое будет под силу сверхразумам будущего; или уже где-то в далекой галактике какие-нибудь сверхцивилизации, начавшие свой путь развития раньше нас, смогли сделать это. Для них все наши представления о мире могут быть сравнимы с тем, как мы пренебрежительно думаем о наших предках с их представлениями о том, что земля плоская. Может быть разница еще больше, и как уже говорилось, по отношению к ним мы вообще можем быть сравнимы только с бактериями. Конечно, нельзя сказать, что трансцендентность можно «понять», поскольку это противоречит ее сути, вероятно, тут применим другой глагол. Да и вряд ли это можно описать словами, стоит попытаться и становится очевидным, что нам пока такое недоступно.

И хотя подобные рассуждения уже ближе к философии, чем к науке, некоторые из ученых имели свои представления на этот счет. Гейзенберг писал, что любой человек, начавший увлекаться наукой, неизбежно становится атеистом, но тот, кто познает глубину научных истин, откроет в себе бога. Гейзенберг, как и Эйнштейн, был основателем современной физики. Первый открыл принцип неопределенности, главный в квантовой механике, а второй являлся единоличным родоначальником теории относительности. Они были не согласны друг с другом по многим аспектам, но под словом «бог» имели в виду одно и тоже. Бог для Гейзенберга и Эйнштейна был не всевидящим координатором человеческих судеб, каким рисует его религия, поскольку они считали, что в масштабах вселенной люди слишком незначительны, чтобы у бога могло быть до них какое-то дело. Их бог это есть те самые трансцендентные основы бытия, на которых держится вся математика и физика, функционирует наш разум, и за счет которых существует вселенная.

В завершении хотелось бы отобразить эту непостижимость на карте, среди маршрутов пройденного нами путешествия. Ее можно представить как место, где сходятся все дороги, ту точку дальше которой в нашем странствии мы продвигаться уже не можем, потому что, куда бы мы ни пошли, нас ждет лишь возвращение назад. Но ведь мы уже знаем про один перекресток, тот, откуда начали свое путешествие. Как прямые дороги могут пересекаться еще в каком-то месте. Такое может случиться только на поверхности сферы. Например, на Земле все прямые дороги, идущие с северного полюса, обязательно пересекутся на южном полюсе. Разница в том, что планета, по которой мы путешествовали это не одно из космических тел, а весь познаваемый нами мир, и нет ничего за ее пределами.

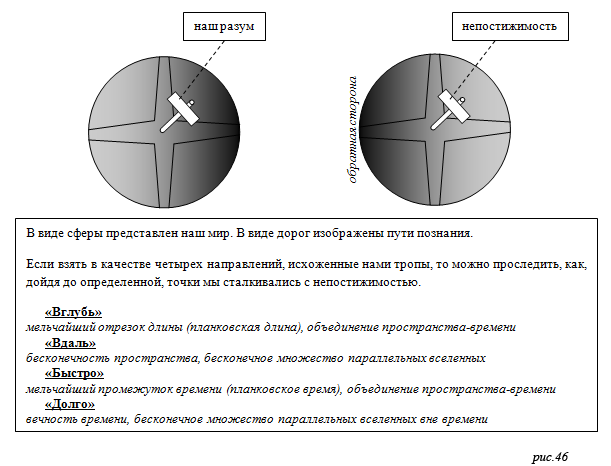
Перекресток, с которого мы начинали свой путь в разные стороны символизировал нашу повседневность, то место где обычно обитает наш разум. Непостижимость – тоже перекресток, где сходятся все эти дороги, но только он находится на другой стороне этой планеты познания (см. рис.45). Мы прошлись только по четырем дорогам, на самом же деле дорог, по которым в процессе познания может пойти наш разум, великое множество, но все они, так или иначе, сойдутся в одном месте. Поскольку находясь на северном полюсе невозможно дальше идти на север, то и нам некуда дальше двигаться в точке непостижимости. Любое путешествие должно рано или поздно завершиться, даже если в ходе него пришлось пройти расстояние длиною в вечность.

© Лихачев С.С. 2010 г.