
Часть I Числа
Любому мыслимому объекту можно сопоставить число - одно из следствий Аксиомы выбора
Есть такая наука, гугология называется. По сути, можно сказать, что это такой особый подраздел математики, в котором изучаются большие, сверхбольшие, гипербольшие и даже бесконечные числа. Можно конечно считать ее вымышленной, несерьезной и бесполезной, но обычно принято вместо этого говорить более мягко: "занимательная наука", подразумевая, что она является лишь забавой для математиков - развлечением на тему: кто придумает число больше. То, что наука "вымышленная" - тут не поспоришь, поскольку даже название свое берет от "вымышленного" числа - гугол (googol). Это наименование придумал девятилетний племянник американского математика Эдварда Казнера, исключительно ради забавы, чтобы обозначить число с сотней нулей после единицы[1]. Однако то, что это число "вымышленное" отнюдь не значит, что оно не настоящее, современная наука вполне способна оперировать этим числом для описания реальных физических величин. А ныне крупнейшая IT-компания даже была названа в честь этого числа (правда из-за патентной политики предварительно исказив написание - google).
На самом же деле занимательность этой науки может быть очень полезна как для математики так и для философии. Как вы увидите, вопрос о существовании сверхбольших чисел напрямую граничит с такими вопросами как "где границы возможностей человеческого разума?", "насколько велик ментальный мир человека?", "каким образом математика рождается в наших головах?", "есть ли пределы познания окружающего мира человеком?". Если вы хоть раз задавались вопросом, какое число самое большое или есть ли что-нибудь больше бесконечности, значит где-то в душе вы тоже любите гугологию. Сегодня, не имея математической подкованности, так просто понять все что в ней происходит навряд ли получится. К тому же популярной литературы на эту тему на русском языке практически не существует. Поэтому я и решил написать популярную книгу, в которой попробую максимально доступно объяснить, что же такое гугология.
Вероятно стоит предупредить, что пусть это и популярная книга, это книга по математике, и не будет легким чтивом для всех. И несмотря на то, что я попытался, как можно проще рассказать обо всем этом, все равно, для осмысления придется не хило напрячь мозги. Тем не менее школьного курса математики вам будет более чем достаточно. В книге будут присутствовать формулы, и всякие математические термины, которые я буду пытаться по возможности объяснить, уменьшить порог вхождения, упростить их понимание. Книга будет полезна как для любителей-энтузиастов, так и для специалистов, если первые справятся с нарастающей сложностью, а вторые с обилием аналогий и объяснений "простых" вещей. Книга построена по тому же принципу, что и вся гугология, рассказ буду вести от меньших чисел к бо́льшим, и по мере того как мы будем сталкиваться со все бо́льшими числами сложность повествования будет нарастать, и для понимания последующих больших чисел, будет необходимо понимание предыдущих.
В самом начале своего пути по гугологии давайте разберем как мы вообще воспринимаем и записываем числа. Для этого я должен объяснить, что такое нотации, и не те, которые родители читают своим детям, а что такое математические нотации. Грубо говоря, нотация - это способ записи числа. Первыми нотациями были либо зарубки на деревьях, либо узелки на веревках, либо штрихи на глине - самое простое представление и запись чисел - назовем это натуральным видом. Сколько оленей увидел охотник, столько же зарубок и сделал. Итак, все числа которые можно представить в натуральном виде, называются натуральными. Но натуральный вид это не всегда удобно, особенно если необходимо записать очень большое число.
Вот так выглядело бы число 1000 в своем натуральном виде у древнего человека, который делал зарубки на дереве:

Хотя, надо признаться, что от такого количества зарубок дереву мог быть нанесен непоправимый ущерб. Естественно людям понадобился иной вид записи чисел, или говоря на языке математики, им понадобился новый вид нотации. Этот вид называется - цифрами. Каждая цифра символизирует какое-то число. Конечно придумывать цифры для каждого числа это будет не упрощением, а скорее наоборот усложнением для счета. Необходимо было придумать как скомбинировать натуральный вид числа и цифры. И вот с этого момента внутри нотации появляется функция. Что такое функция - позже мы разберем подробнее, это очень глубокое и фундаментальное понятие, пока упрощенно можно сказать, что функция в математике это такая штука, в которую ты что-то подставляешь, и получаешь какой-то результат. Все виды нотаций, использовавшиеся любой древней цивилизацией, и наша современная десятичная нотация, по сути, являются функциями.
Самый простой способ - это непозиционная цифровая нотация. Ставим все цифры в ряд и складываем, то есть в нотации заложена всего одна функция - сложение. Одна из самых древнейших нотаций для записи чисел, использовалась соответственно одной из самых древнейших цивилизаций. Цифры египтяне обозначали иероглифами. Это очень интересный и важный факт - появление письменности всегда вело к появлению математики. Лингвистика, которую в школе изучают в рамках курса родного языка, как оказывается тесно связана с математикой, дисциплиной, которую в школах традиционно принято отделять, начиная с самого первого класса. Первые цифры и нотации произошли из языковой письменности (от пиктограмм, иероглифов, букв), и как вы увидите в дальнейшем, выходит что язык и математика тесно связаны - и то, и другое формы проявления абстрактного мышления, сопряженные грани одного ментального мира. Математика напрямую зависит от языка на котором формулируется, чем сложнее формальная система знаков, тем более сложные математические понятия можно на ней выразить. Но вернемся к египетским цифрам. Цифры вводились египтянами только для обозначения чисел кратных 10, так что можно назвать их систему счисления - непозиционной десятичной. Единица (1) как и у большинства народов обозначалась палочкой, десятка (10) - закорючкой символизирующей след копыта, сотня (100) - тоже была простым иероглифом, что обозначал петлю веревки, тысяча (1000) - кувшинка, 10000 - палец, 100000 - личинка жабы, 1000000 - человек с поднятыми руками[2].
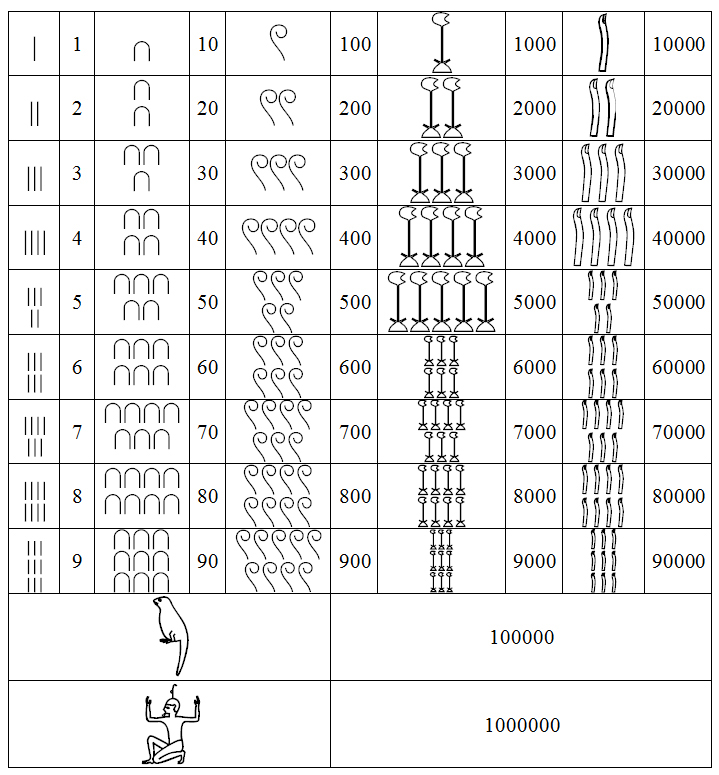
Принцип построения числа был простой. Цифры группировались в натуральном виде, не превышая своим количеством числа девять. Располагать их относительно друг друга можно было как слева так и справа, или даже сверху и снизу, позиция не имела значения, ведь система была непозиционной, в основе которой лежала лишь функция сложения, а как мы помним из школы: от перестановки слагаемых сумма не меняется.

Древнегреческая система счисления была устроена похоже, по непозиционному принципу, но в ней уже было меньше натурального вида записи, в этом отношении она была намного ближе к арабской системе счисления, которой мы сейчас пользуемся. Для каждого числа меньше десяти (10) существовала цифра его обозначающая, аналогично существовала цифра для каждого числа меньше сотни (100), но кратного десяти (10), ну и следовательно для каждого числа меньше тысячи (1000), но кратного сотне (100), тоже существовала цифра. Ну а дальше они просто ставились в ряд и складывались. Конечно смысл имело только сопоставление в ряд чисел разных порядков, что уже было первым шагом к понятию числовых разрядов. С математической точки зрения порядок записи значения не имел, но было принято записывать цифры слева направо в порядке убывания. В качестве цифр использовались буквы греческого алфавита, ну а чтобы отличить их от самих букв на письме, буквы обозначающие цифры подчеркивались сверху. В разных регионах и разные периоды истории принципы записи греческих цифр могли меняться, например могли использоваться как строчные, так и прописные буквы
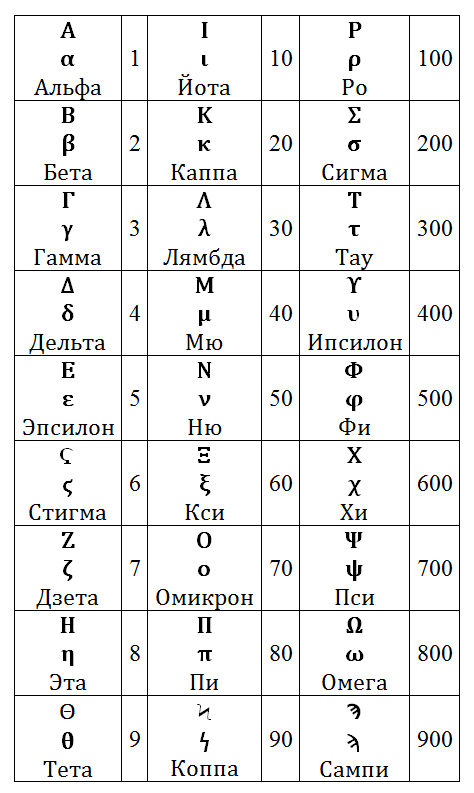
Вообще греческий алфавит не мешало бы выучить любому человеку, кто занимается или интересуется математикой, да и вообще физическими науками. Сегодня греческими буквами принято обозначать физические величины и константы, названия в астрономии, переменные в алгебре и теории чисел, обозначения в геометрии. Далее в повествовании греческие буквы будут встречаться постоянно, символизируя те или иные понятия из мира больших чисел, поэтому предлагаю и вам детально ознакомится с греческими буквами. Хотелось бы отметить, что букв Стигма, Коппа и Сампи, символизирующих числа 6, 90 и 900, соответственно, в современном греческом алфавите уже нет, они считаются устаревшими. Особого внимания заслуживает Сампи, она использовалась для создания цифр символизирующих большие числа. Комбинируя ее с другой буквой, которую необходимо было написать в верхнем левом углу от Сампи, создавалась цифра, которая была в 1000 раз больше исходной. Каждый раз, добавляя еще одну букву Сампи в правый угол цифры, мы так же могли тысячекратно увеличить цифру (это один из древних способов записи, позже он изменялся)[3].
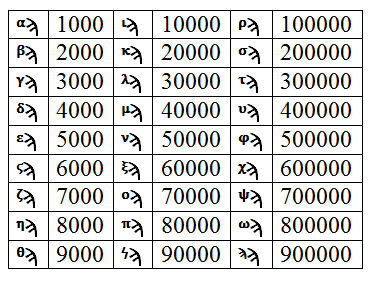
Пусть греческая система счисления и была непозиционной, но все же позволяла так же коротко записать число, как и современная арабская система счисления.
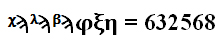
Древнерусская система счисления по своим принципам и функции заложенной в ней была полной копией древнегреческой системы, только вместо греческих букв использовалась кириллица.
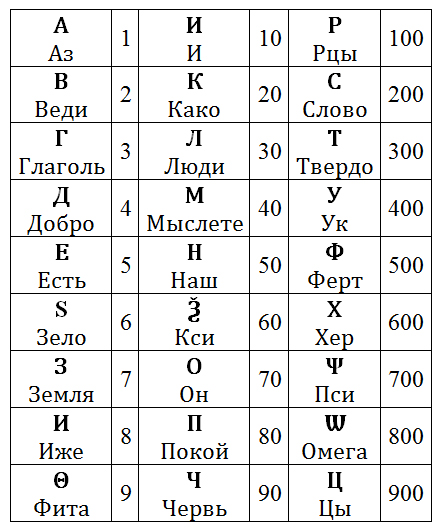
Однако я не могу не отметить развитую систему счисления больших чисел, которая фактически была древнерусской гугологией и называлась эта система Великий счет. При помощи специальных диакритических знаков можно было довести десятичную значность цифры до невероятных по тем временам масштабов. Можно даже сказать, что древнерусский Великий счет был рекордсменом в создании самых больших чисел, которые можно выразить одной цифрой. Основными числительными Великого счета были следующие:

Для выражения цифр Великого счета была использована логарифмическая нотация, о которой подробно будет рассказано далее. Пока вам достаточно знать, что En = 10n = числу с n-ным количеством нулей после единицы. Таким образом, используя Великий счет, в Древней Руси уже могли выразить число гугол следующим образом: E100 = десять тысяч колод. При этом максимально возможным круглым числом, которую мог создать Великий счет, была цифра:

В отношении краткой записи известная всем римская система счисления кажется шагом назад по сравнению с древнегреческой и древнерусской, но стоит отметить, что в ней была заложена более сложная функция, в которой позиция цифры имела значения, хоть и считается эта система тоже непозиционной. Цифры вводились аналогично египетской системе счисления для каждого десятичного порядка, но еще в добавок для половины от этого значения. Это так же были буквы, но уже естественно, латинского алфавита (
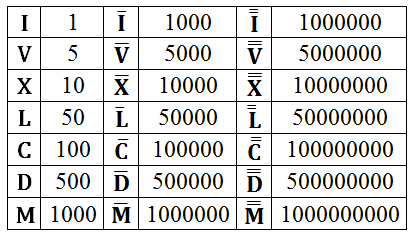
Все же несмотря на то, что запись числа была и намного больше и намного сложнее воспринималась, римская система счисления продержалась в Европе на протяжение всего средневековья. С одной стороны использование натурального вида давало возможность запоминать меньше цифр, но для счета больших чисел эта система оставалась неудобной.
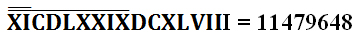
На смену ей пришла всем нам известная и использующаяся ныне по всему миру арабская система счисления, или позиционная десятичная нотация. Европейцы заимствовали ее у арабов, те у индусов, а индусы создали ее на основе принципов китайской системы счисления, которая вероятно так же стара как и греческая. В качестве цифр китайцы тоже использовали иероглифы как и египтяне, но все же функция заложенная в основе китайской системы счисления была сложнее, чем функции греческой или египетской систем. Это было не просто сложение чисел, которые символизировали цифры, но в функции была еще и операция умножения, поэтому эту систему называют мультипликативная. Цифры объединялись в группы, в которых происходило умножение, а уже сами группы потом складывались, так что можно сказать что порядок в ней имел куда бо́льшее значение, поскольку его несоблюдение нарушало работу функции, поэтому иногда еще эту систему называют полупозиционная. Китайские цифры делились на десятичные:
В этой системе уже появились зачатки понятия разрядности, но она еще не была полностью позиционной, тем не менее ей до сих пор пользуются в современных Китае и Японии. Создание же позиционной системы счисления не было бы возможным без изобретения цифры обозначающей ноль (0), которую независимо придумали в Индии, Вавилоне и Маянской Мезоамерике (при этом Вавлоняне пользовались шестнадцатиричной позиционной системой счисления, а Индейцы Майя двадцатиричной системой счисления, так что будем считать что родиной современной системы счисления является именно Индия). Многим может показаться, что это совсем не тянет на изобретение, ведь ноль кажется нам таким очевидным. Однако древним казалась абсолютно бессмысленной и даже в чем-то деструктивной идея формальной записи пустоты. И правда, зачем давать обозначение "ничему", однако именно абстрактное постижение такой вещи как пустота дает ключ к развитию математики, позже это произошло еще раз когда изобретение пустого множество привело к созданию теории множеств, уникальному математическому инструменту, но об этом мы поговорим в следующей части, а пока вернемся к арабской системе счисления. Ноль делает ее полностью позиционной нотацией, которая содержит в себе намного более сложную функцию, в ее составе есть не только операции сложения и умножения, но еще и возведение в степень. Расположение, в котором мы расставляем арабские цифры в позиционной десятичной нотации, играет важную роль, оно определяет кратность десятичному порядку, на который нужно домножить цифру, и называется разрядом или значностью цифры. Без нуля было бы невозможно записать таким образом числа вроде 103, 1108, и т.п. Вот так выглядит функция десятичной нотации:
Однако с самого детства, как только мы научились считать, эта формула настолько прочно поселилась в нашем мозгу, что нам сейчас кажется, что мы всегда понимали десятичную нотацию. Но это не так. Многие малые дети, которые обучаются счету (возможно и вы были в их числе), доходя до числа 11 пытаются придумать ему либо особое название, либо особую запись, потому что понятие числовых разрядов для ребенка очень сложно и не сразу поддается осознанию. Сейчас же мы настолько привыкли к десятичной нотации, что нам кажется, что мы понимаем масштабы очень больших чисел. Однако это не так. Любая нотация, которую осваивает человек создает ложное впечатление о том, что человек понимает и осознает масштабы чисел, которые могут быть в ней записаны. Взять хотя бы миллион (1000000), число таких масштабов можно записать не только в десятичной системе счисления, но практически все древние нотации позволяли очень коротко записать это число. Однако наглядный масштаб этого числа даже сейчас для человека почти непостижим. Вернитесь к рисунку №2, где мы штрихами изображали тысячу и представьте, что каждый штрих из тех что выше, превратился во всю эту совокупность штрихов. Или попробуйте пересчитать все точки из рисунка, что ниже:




















Ну как? Получилось осознать масштаб числа? Нет. Тогда, значит зачастую, когда мы говорим "миллион", то у нас происходит подмена понятий и мы представляем не число, а его десятичную нотацию или какое-то иное его представление. Полагаю, что скорее всего вы поверили мне и не стали пересчитывать весь миллион точек из рисунка №10, да и навряд ли стали проверять тысяча ли палочек в рисунке №2. Ведь правда, сосчитать вслух даже до одной тысячи весьма утомительное занятия, делая это не торопясь, и произнося одно число в секунду, вы будете считать 16 минут 40 секунд. Ну а если решитесь досчитать вслух до миллиона, пересчитав все эти точки, то у вас займет это немного немало 11 дней, 13 часов и 46 минут, и сделать это без перерывов будет невозможно.
А теперь попробуйте вообразить "миллиард" (или "биллион" - как его принято называть в американской системе именования больших чисел), для этого представьте что каждая из этих точек на рисунке №10 превратилась в совокупность штрихов из рисунка №2. Сложно? Но это еще не все... Давайте теперь попробуем пересчитать все эти штрихи в получившемся миллиарде, считать будем так же со скоростью один штрих в секунду. Так вот, если считать с такой скоростью, чтобы пересчитать весь миллиард на это уйдет примерно 31 год, 251 день и 8 часов. Страшно подумать, но средняя продолжительность жизни содержит всего чуть больше двух миллиардов секунд. Всего на земле проживает более 7 миллиардов людей, и чтобы произнести имя каждого человека живущего на планете потребуется более 200 лет, что больше любой человеческой жизни.
Немного проще осознавать большие числа, подключая пространственное мышление. Так, например, в кубическом сантиметре тысяча кубических миллиметров, в кубическом дециметре миллион кубических миллиметров, в кубическом метре миллиард кубических миллиметров. Используя систему вложенных объемов мы можем представить достаточно большие числа.
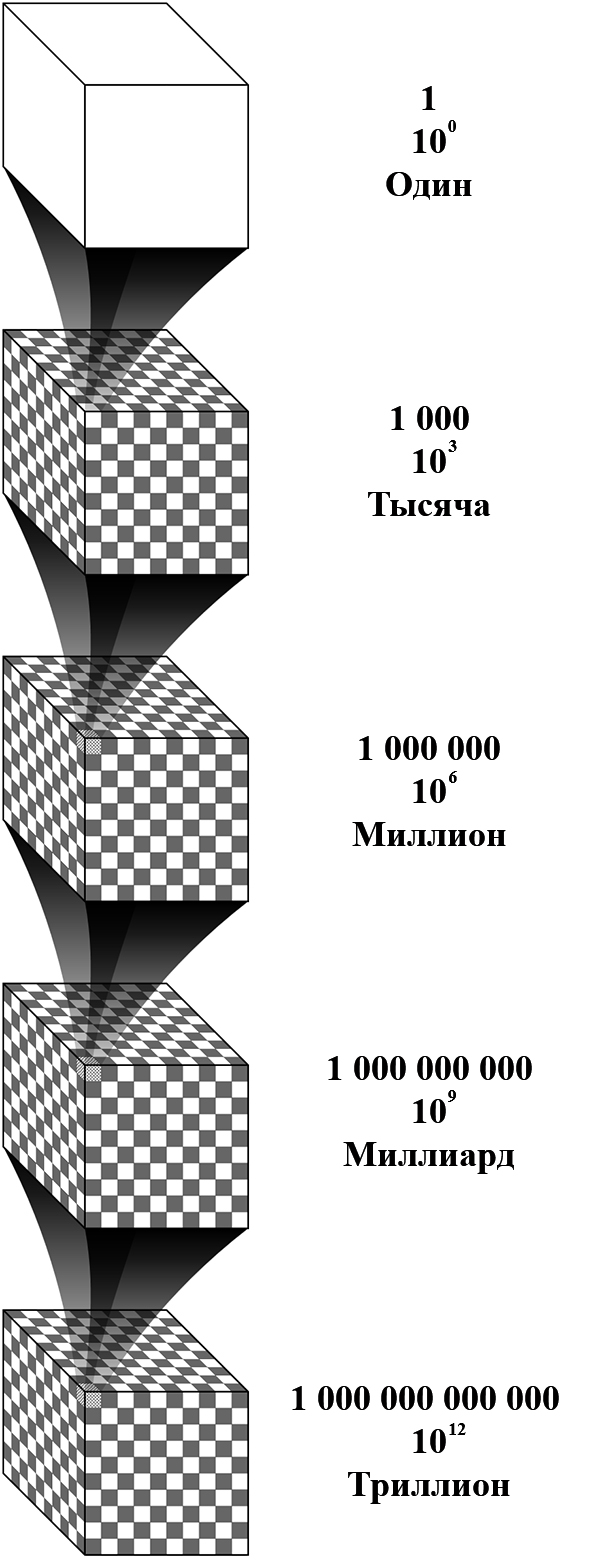
Продолжая эту цепь из вложенных кубов можно составить иерархию из все бо́льших и бо́льших чисел, с возрастающей тысячекратностью, в которой с каждым новым числом количество нулей после единицы увеличивается на три. Числа приведенные ниже в таблице №1 входят в так называемую американскую систему именования больших чисел.
| 106 | Миллион | |
| 109 | Биллион | |
| 1012 | Триллион | |
| 1015 | Квадриллион | |
| 1018 | Квинтиллион | |
| 1021 | Секcтиллион | |
| 1024 | Септиллион | |
| 1027 | Октиллион | |
| 1030 | Нониллион |
Как многие заметили, проще будет записывать большие числа не указывая все их ноли на письме, а записывая их в виде степеней десятки. Например:
Чтобы дать названия числу необходимо разобрать его логарифмическую запись (10n, где n - обозначает число нулей после единицы) следующим образом. Из числа n, обозначающего число нулей, необходимо отнять 3, и затем поделить его на 3, целую часть от деления запомнить как число k, а остаток от деления запомнить как число m. Далее, если
| № | единицы | десятки | сотни |
| 1 | ун | деци | центи |
| 2 | дуо | виджинти | дуценти |
| 3 | тре | триджинти | тресценти |
| 4 | кваттор | квадраджинти | квадридженти |
| 5 | квин | квинкваджити | квиндженти |
| 6 | секс | сексаджинти | сесценти |
| 7 | септен | септуаджинти | септидженти |
| 8 | окто | октоджинти | октиндженти |
| 9 | новем | нонаджинти | нондженти |
Конечно, вот так сложно разобраться в принципах именования числа, поэтому давайте разберем на примерах.
Число 1033 имеет
Пример посложнее, давайте назовем гугол (10100) по правилам расширенной американской системы именования больших чисел
Ну и совсем уж сложный пример, возьмем 101000 - число с тысячей нулей после запятой.
Кроме перечисленных выделяют еще одну приставку для единицы в тысячном разряде числа k, называется "миллини". Что дает возможность дать название числу
Теперь, я думаю читателю понятно, почему американская система именования больших чисел не получила большого распространения, ведь намного проще сказать 10 в n-ной степени, чем запоминать все эти приставки и принципы их сочетания друг с другом. Логарифмическая нотация проще, но она еще сильнее отдаляет нас от реального понимания масштаба числа. Нам может казаться, что разница между числами 1030 и 1042 невелика, но на самом деле второе число больше первого в триллион раз (
Начнем с 1010 - десяти миллиардов, это больше чем количество людей проживающих сейчас на Земле. Самая большая известная нам молекула это человеческая хромосома, она как раз состоит из 10 миллиардов атомов[6]. Всего же за всю историю человечества на земле проживало более 100 миллиардов людей (1011), что в десять раз больше[7]. Однако деревьев на планете еще больше, около трех триллионов[8], и примерно один триллион (1012) из этого количества растет на территории СНГ, что в десять раз больше чем число людей когда-либо ступавших по планете. Но в микромире все еще богаче, так например, в человеческом теле 40 триллионов (4×1013) клеток[9], что в четыреста раз больше числа всех людей, которые когда-либо существовали. При том, что каждая из них содержит 23 хромосомы. Но еще более удивительно то, что в человеческом теле живет почти столько же бактерий[9], причем человек рождается почти без бактерий и приобретает их в первые несколько лет своей жизни. Получается, что люди сами по себе являются целым миром микроорганизмов, куда большим, чем привычный нам мир людей. А еще, если всю ДНК из всех клеток человеческого организма объединить и вытянуть в одну спираль, то ее длина будет примерно 100 триллионов (1014) метров[10].
Следующее именное число после триллиона это квадриллион (1015), и многим наверное по-прежнему сложно осознать, сколько это - квадриллион. Большие цифры мы привыкли слышать, когда речь идет о суммах, для многих заветных и недостижимых, о которых говорят в новостях экономики или пишут в модных журналах про богатых людей. Так вот квадриллион долларов это примерно столько сколько сейчас имеется денег на земле. И речь не только о напечатанных банкнотах, ведь в сущности бумажные деньги - это лишь коммерческий договор с центральным банком государства, квадриллион долларов - это оценка всей экономической деятельности на планете земля. Давайте посмотрим на таблицу №3, чтобы, поэтапно сравнивая стоимость вещей, добраться до этой суммы. Все цены в таблице приведены на начало 2020 года, либо на момент их последней оценки.
| $$$ | эквивалентные блага |
| 0,005 | 1 грамм меди[11] |
| 0,05 | целлофановый пакет |
| 0,1 | конфета |
| 0,3 | проезд на автобусе |
| 0,5 | 1 грамм серебра[12] |
| 1 | проезд на метро |
| 2 | чашка кофе |
| 3 | большой бургер |
| 5 | проезд на такси |
| 10 | обед в ресторане |
| 40 | компьютерная игра |
| 50 | 1 грамм золота[13] |
| 250 | деловой костюм |
| 500 | диван |
| мощный игровой компьютер | |
| бюджетный автомобиль | |
| алмаз среднего качества весом 1 грамм[14] | |
| квартира в большом городе | |
| большой дом в большом городе | |
| Каберне Кричащий Орел (самое дорогое вино)[15] | |
| [пачка 100$-купюр размером с микроволновку] | |
| Постройка средней школы на 300 учеников[16] | |
| 1 грамм Калифорния (самое дорогое вещество)[17] | |
| Феррари 250 GTO (самый дорогой автомобиль)[18] | |
| пассажирский аэробус[19] | |
| 450 000 000 | "Спаситель мира" Леонардо да Винчи (самая дорогая картина)[20] |
| Ланай, остров на Гавайях (самый дорогой проданный остров)[21] | |
| [пачка 100$-купюр размером с грузовой лифт] | |
| Симфония морей (самый большой лайнер на 6700 пассажиров)[22] | |
| Стелс-бомбардировщик (самый дорогой самолет)[23] | |
| 2 500 000 000 | Стоимость полета на Луну[24] |
| Абрадж аль-Бейт в Саудовской Аравии (самое дорогое здание)[25] | |
| 40 000 000 000 | Стоимость полета на Марс[26] |
| состояние Билла Гейтса (второго самого богатого человека)[27] | |
| 115 000 000 000 | состояние Джеффа Безоса (самого богатого человека)[27] |
| 300 000 000 000 | стоимость всего добытого серебра на планете[28] |
| [пачка 100$-купюр размером с пятиэтажный дом] | |
| 1 200 000 000 000 | Стоимость Apple (второй самой дорогой компании)[29] |
| 1 500 000 000 000 | состояние династии Морганов (второй самой богатой династии)[30] |
| 1 700 000 000 000 | Стоимость Saudi Aramco (самой дорогой компании)[29] |
| 2 500 000 000 000 | состояние династии Ротшильдов (самой богатой династии)[30] |
| 3 000 000 000 000 | стоимость всей добытой меди на планете[31] |
| 5 000 000 000 000 | все наличные деньги на планете (монеты, банкноты)[32] |
| 8 000 000 000 000 | состояние всех миллиардеров планеты[27] |
| стоимость всего добытого золота на планете[33] | |
| 14 000 000 000 000 | ВВП Китая[34] |
| ВВП США[34] | |
| стоимость всех земельных участков[35] | |
| 33 000 000 000 000 | стоимость всей коммерческой недвижимости на планете[35] |
| 60 000 000 000 000 | 1 грамм антивещества[36] |
| 70 000 000 000 000 | состояние всех миллионеров планеты[37] |
| 80 000 000 000 000 | все деньги на планете (монеты, банкноты, депозиты)[32] |
| Мировой ВВП[38] | |
| 200 000 000 000 000 | стоимость всей криптовалюты[32] |
| 220 000 000 000 000 | стоимость всей жилой недвижимости на планете[35] |
| 250 000 000 000 000 | Мировой долг (сумма всех кредитов, частных и государственных)[39] |
| стоимость всей недвижимости на планете[35] | |
| средняя оценка стоимости всех ценных бумаг на планете[32] | |
| [пачка 100$-купюр размером с Дубайскую башню] |
Итак, пачки 100$-купюр размером с Дубайскую башню хватит чтобы купить все что имеется на Земле. Но если у какого-нибудь мецената внезапно окажется столько денег, это не значит, что он сможет скупить всю Землю, просто мировая экономика тут же испытает сильную инфляцию и деньги начнут обесцениваться по мере того, как этот меценат начнет скупать все что есть на планете. Но что если все эти гипотетические 100$-купюры разложить по поверхности Земли, тогда их хватит, чтобы покрыть всю территорию Арабских Эмиратов. Сколько же денег надо, чтобы покрыть всю сушу нашей планеты? Что ж, для этого понадобится более 10 квадриллионов (1016) купюр. А если мы будем выкладывать 50-центовые монеты, то даже если мы покроем ими не только сушу, но дно всех морей и океанов, нам понадобится около 100 квадриллионов (1017) монет.
Следующее именное число на очереди - квинтиллион (1018) - это в тысячу раз больше квадриллиона. Квинтиллион - это так много, что даже если бы вся земля была бы усеяна деньгами, то все равно едва бы набралась такая сумма. Это так много, что с момента зарождения вселенной прошло всего половина квинтиллиона секунд. 2 квинтиллиона - столько насекомых обитает на нашей планете[40]. Это значит, что на каждого человека, живущего на земле, приходится четверть миллиарда насекомых, это столько сколько людей проживает в Соединенных Штатах. Если бы всех насекомых равномерно распределить по поверхности суши, то на каждом квадратном сантиметре их сидело бы не меньше двух особей, что может ввергнуть в шок любого инсектофоба. Осознав это количество, сложно по-прежнему считать себя хозяевами нашей планеты. Насекомых на планете конечно много, но это в пять раз меньше, чем атомов содержится в одной песчинке, а их там, как нам подсказывает формула Авогадро, около 10 квинтиллионов (1019). Но космос, он настолько же большой насколько малы атомы, если измерить размеры нашей галактики Млечный путь в метрах, то получится примерно 100 квинтиллионов (1020).
Если предыдущие именные числа, иногда можно услышать в обиходной речи, чаще правда внутри гиперболических оборотов, то многие никогда даже не слышали о секстиллионе (и даже проверка орфографии в программе, в которой я набираю текст, подчеркнула это слово). Секстиллион (1021) - это в тысячу раз больше квинтиллиона, столько примерно потребовалось бы 50-центовых монеток, если бы мы могли ими выложить всю поверхность Солнца. Секстиллион примерно равен числу всех песчинок на Земле[41]. Надо признаться мы не первые кто пытается измерять песчинками большие числа, еще Архимед в своем, пожалуй первом в истории труде по гугологии, Псаммит "Исчисление песчинок", пытался измерить размер вселенной в песчинках. Для его времени расчеты были достаточно точными, но сегодня мы знаем что он недооценил масштабы природы. А еще Архимеда, который делал все свои расчеты на примитивном абаке, удивили бы современные масштабы развития вычислительных технологий. Интересен следующий факт, песок так же как и электронный транзистор сделан из кремния, но транзисторы могут выполнять логические операции и благодаря сегодняшним технологиям могут достигать нанометровых размеров, миллиардами размещаясь на процессорах наших компьютеров. Экстраполируя данные прошлых лет[42], можно сказать, что всего на земле на начало 2020 год было выпущенно более 10 секстиллионов (1022) транзисторов, в десять раз больше чем песчинок на планете. Почти то же число бактерий живет суммарно во всех людях на планете. А еще столько же молекул содержится в чайной ложке воды и столько же чайных ложек воды содержится в Мировом океане. Песчинки и капли воды в рамках всей планеты, так же малы как атомы и молекулы в рамках этих песчинок и капель. Однако космос еще более велик, по приблизительным оценкам число звезд и планет в наблюдаемой вселенной около 100 секстиллионов (1023), это в 100 раз больше, чем число песчинок, которые можно найти на Земле[43].
Септиллион (1024), этим числом можно измерить массу Земли, получится 6 септиллионов килограмм. Так же этим числом заканчивается таблица приставок СИ (Стандартов Измерения Международной системы единиц. Примечание: заканчивалась, пока ее не расширили в 2022 году). Эти приставки, во всяком случае относительно небольшие из них, знакомы всем. Их добавляют к единицам измерения для обозначения больших чисел или малых дробей (отрицательная степень десятки символизирует десятичную дробь, в которой число нулей перед единицей равно значению степени, например
| иоттаметр | Им | 1024 | диаметр сверхскопления галактик |
| зеттаметр | Зм | 1021 | диаметр самой большой из известных галактик |
| эксаметр | Эм | 1018 | толщина рукава спиральной галактики |
| петаметр | Пм | 1015 | расстояние до самых отдаленных комет |
| тераметр | Тм | 1012 | радиус орбиты Сатурна |
| гигаметр | Гм | 109 | диаметр Солнца |
| мегаметр | Мм | 106 | средняя длина горной цепи |
| километр | км | 103 | высота Анхеля (самого высокого водопада) |
| гектаметр | гм | 102 | диаметр футбольного поля |
| декаметр | дам | 101 | высота трехэтажного дома |
| метр | м | 100 | длина мужской ноги |
| дециметр | дм | 10-1 | ширина мужской ладони |
| сантиметр | см | 10-2 | ширина ногтя на мизинце |
| миллиметр | мм | 10-3 | размер блохи |
| микрометр | мкм | 10-6 | размер бактерии |
| нанометр | нм | 10-9 | диаметр молекулы ДНК |
| пикаметр | пм | 10-12 | ширина электронных орбиталей в атоме |
| фемтометр | фм | 10-15 | диаметр атомного ядра |
| аттометр | фм | 10-18 | радиус рассеивания кварков и электронов |
| зептометр | зм | 10-21 | радиус рассеивания нейтрино |
| иоктометр | им | 10-24 | длина волны самых мощных космических лучей |
Факты в таблице я привел без ссылок, потому что они уже считаются общеизвестными, и даже привычными для любого физика, так же как привычными для него должны быть эти приставки, которые можно добавлять к любым единицам измерения, избегая при этом использования названий больших чисел или логарифмической записи. Однако есть одно исключение, для измерения информации обычно эти приставки используются по иным правилам. Вместо кратности 103×n при измерении информации используется кратность 210×n, то есть каждая следующая приставка (исключая "дека" и "гекто") больше другой не в
| байт | б | 20 | =100 | один пиксель в изображении низкого качества одна буква текста одно целое число (от 1 до 256) |
| килобайт | кб | 210 | =1,024×103 | иконка в интерфейсе одна страница текста одно целое число (от 1 до 28192) |
| мегабайт | Мб | 220 | ≈1,048×106 | фотография среднего качества минутная аудиозапись в формате mp3 одно целое число (от 1 до 28388608) |
| гигабайт | Гб | 230 | ≈1,074×109 | часовой видеоролик среднего качества объем текста всех книг из городской библиотеки одно целое число (от 1 до 28589934592) |
| терабайт | Тб | 240 | ≈1,01×1012 | объем данных персонального компьютера весь сериал "Игра престолов" в Utlra HD качестве одно целое число (от 1 до 28796093022208) |
| петабайт | Пб | 250 | ≈1,126×1015 | ежедневный трафик крупной социальной сети[44] компьютерная графика для голливудского фильма[45] одно целое число (от 1 до 29007199254740992) |
| эксабайт | Эб | 260 | ≈1,153×1018 | ежегодный мировой интернет-трафик (начала 2000-ых)[46] информации содержится в одном миллиграмме ДНК[47] одно целое число (от 1 до 29223372036854775808) |
| зеттабайт | Зб | 270 | ≈1,18×1021 | ежегодный мировой интернет-трафик[46] сто газет, прочитанные каждым человеком на планете[44] одно целое число (от 1 до 29444732965739290427392) |
| иоттабайт | Иб | 280 | ≈1,209×1024 | вся когда-либо произнесенная человеческая речь в формате mp3[44] в 10 раз больше, чем весь объем цифровой информации на земле[48] одно целое число (от 1 до 29671406556917033397649408) |
Поскольку Закон Мура не прекращаясь работает, хочу предупредить читателя из будущего, что так же как и в предыдущих таблицах, все данные собраны на момент начала 2020 года, и именно в этой таблице многие цифры уже совсем скоро могут многократно измениться. Так же хочу, чтобы вы обратили внимание на третью строчку в каждой строке данной таблицы. Даже особо не вдаваясь в подробности кодирования двоичной информации, на основе ее можно сделать вывод, что у каждого объема информации есть максимальное число, которое в этом объеме можно закодировать. А значит, что и всегда существует такое число, которое нельзя будет закодировать, поскольку не хватит объема памяти. Это очень важная деталь, которую мы в следующей части рассмотрим подробнее, и как выяснится, это окажется глубокой математической концепцией.
Для следующего числа даже не существует приставки для единиц измерения, поскольку масштабы этого числа уже соизмеримы с масштабами известной нам вселенной (примечание: не существовало на момент написания этих строк, до 2022 года, когда приставки СИ расширили еще четырьмя: ронна, кветта для кратных величин и ронто, квекто для дольных). Сверхскопления галактик это самые крупные известные нам структуры во вселенной, но их размер в 1000 раз меньше, чем размеры вселенной доступной наблюдению. Диаметр наблюдаемой вселенной почти 1 октиллион (1027) метров. Хочу сразу здесь отметить, что это размер не всей вселенной, о нем мы достоверно ничего не знаем, а только той части, которую мы можем видеть. Дело в том, что скорость света конечна, так же как и возраст вселенной и с момента Большого взрыва свет еще не успел дойти до нас с отдаленных областей, более того он и не успеет дойти потому что вселенная продолжает расширяться, а значит для нас вселенная всегда будет ограниченна этой областью доступной для наблюдения, граница которой называется космологическим горизонтом (кроме того мы видим отдаленные области вселенной, такими какими они были миллиарды лет назад, когда вселенная была меньше, то есть не расширилась так как сейчас; однако диаметр, который я привожу здесь это оценка реальных размеров с учетом расширения, которое так же произошло в этих удаленных областях)[49]. Ну а снова сделав реверанс от большого к малому, могу сказать что нужно взять примерно октиллион (1027) атомов водорода (самых легких атомов), чтобы их набралось массой один килограмм.
Идем дальше. Следующее число нониллион (1030), столько примерно насчитывается бактерий на всей земле[50]. Вот кто на самом деле хозяева нашей планеты. Бактерии самые древние ее обитатели, им около 4 миллиардов лет, они появились спустя всего полмиллиарда лет с момента образования планеты, они же прародители всего живого, предки любого ныне обитающего существа, неотъемлемые участники любых процессов жизнедеятельности, без них была бы невозможна жизнь ни в одной экосистеме. Бактерии считаются бессмертными, то есть они не умирают от старости, многие могут впадать в анабиоз на миллионы лет. Бактерии обитают повсюду: на земле, в воде, в воздухе, в живых организмах, даже внутри горных пород. Их настолько много, что если все бактерии равномерно распределить по поверхности планеты, то они покроют ее метровым слоем, и это при том, что их размеры не превышают нескольких микрометров. Бактерии очень маленькие, но элементарные частицы еще меньше и легче, ведь для того чтобы набрался один килограмм электронов их надо взять примерно нониллион (1030) частиц.
Последнее используемое мной число из американской системы именования больших чисел это дециллион (1033), поскольку следующие приводимые мной числа будут увеличиваться больше чем в тысячу раз, и легко можно будет запутаться во всей этой системе приставок, поэтому начиная с дециллиона (1033) мы полностью переходим на логарифмические именования чисел и вместо "...иллионов" будем говорить только "десять в n-ой степени". Но пока что мы еще можем обсудить последнее "...иллион"-ное число, очень важное число, смею заметить: 100 дециллионов (1035). Во столько раз планковская длина меньше метра[51]. Планковской длиной - называют длину, которая наименьшая описывается известными нам законами физики, из которых следует, что на меньших масштабах само пространство-время перестает существовать, а значит ничто физическое не может быть меньше этой длины. Отсюда следует, что существует и минимальный промежуток времени, так же называемый планковским, ведь поскольку быстрее света ничего не может двигаться, то время, за которое свет преодолевает минимально возможную длину, так же будет минимально возможным. Пространство на планковских масштабах представляет из себя пузырящуюся пену, в которой привычные нам пространство и время буквально кипят иногда даже превращаясь друг в друга, и которую еще называют квантовой пеной[52]. По одной из теорий ("космической инфляции" - ее мы еще рассмотрим в дальнейшем) в этой пене могут рождаться пузыри новых вселенных и раздуваться в свое собственное пространство-время[53]. Вторая физическая величина, к которой применимо это число, это интенсивность фундаментальных сил, напрямую связана с плакновской длиной. Гравитация примерно в 100 дециллионов (1035) раз слабее электромагнитной силы (это легко вычислить, если поделить константы связи этих сил). Гравитация - величественная сила, она формирует галактики, звезды и планеты, весь космос подчиняется ей, однако она очень слабая. В качестве примера обычно приводят маленький магнитик, который способен поднять с пола иголку, которую всей своей массой гравитационно удерживает вся наша планета. Поэтому мы можем существовать на поверхности планеты, все из-за этого числа (1035). Поскольку все что мы видим вокруг себя сформировано этими фундаментальными силами. Если величественные космические объекты поражающие своими размерами создала именно слабость гравитации (была бы эта сила сильнее, тогда и космические объекты были бы меньше и плотнее), то мощь электромагнитной силы создала маленькие атомы, способные вступать опять же за счет электромагнетизма в химические связи и в конечном счете порождать живых существ. Но не только за относительные размеры атомов, людей и планет ответственно это число, оно же определяет скорость протекания процессов, ведь чем сильнее сила, тем быстрее происходят взаимодействия, именно поэтому по сравнению с человеческой жизнью космос кажется почти вечным. Все размеры, формы и временные интервалы, о которых мы с вами говорили, напрямую зависят от этого числа, но будь оно иным на несколько порядков это не значит, что все что мы видим было бы больше или меньше чем есть, всего этого вообще могло не быть, поскольку многие взаимодействия бы не произошли. Могло бы не возникнуть химии или самих атомов, тогда вся материя представляла бы собой рассеянные в космосе элементарные частицы, или будь гравитация чуть сильнее, то все бы давно схлопнулось в черные дыры. На масштабах планковских длин гравитация становится сильнее электромагнетизма и там пространства фактически не существует, так же как когда-то не существовало нашей вселенной. По уже упомянутой нами теории космической инфляции собственно и сам Большой взрыв, процесс творения, произошел всего за одну 1035-ную долю секунды с начала времен (в нашей системе отчета; дальше объясню, почему это имеет значение). За это время наш космос раздулся до невероятных размеров[53], гравитация отделилась от других сил, высвободив из небытия отрицательную энергию, а компенсирующая ее положительная энергия, превратилась в материю, сконденсировавшись в виде элементарных частиц. Если бы этот процесс длился чуть меньше, пространство бы схлопнулось обратно в небытие, а если чуть дольше то растянулось бы так, что представляло бы собой пустой безжизненный низкоэнергетический вакуум. На этом, я думаю, стоит сказать "спасибо" числу 100 дециллионов (1035) за то, что создало нашу вселенную такой, какая она есть, в которой мы разумные существа можем обсуждать размеры, масштабы и числа; и будем двигаться дальше.
Теперь продвигаться будем скачками, думаю читатель уже освоился с логарифмической нотацией и осознанием масштаба чисел, поэтому дальше я буду приводить числа одной строкой без их названий и без сравнений с предыдущими числами.
1039 вирусов обитает на земле (в миллиард раз больше чем бактерий)[54]
1041 килограмм - весит самая большая черная дыра (самый массивный объект в известной вселенной)[55]
1043 планковских единицы времени (мельчайший временной промежуток) содержится в одной секунде
1047 калорий - энергия взрыва самой мощной сверхновой (зарегистрированной в известной вселенной)[56]
1049 ватт - мощность столкновения двух черных дыр (мощнее света всех звезд в наблюдаемой вселенной)[57]
1050 атомов содержит в себе наша планета
1053 килограмма - масса наблюдаемой вселенной[58]
1062 планковских единиц длины в диаметре наблюдаемой вселенной
1062 планковских единиц времени прошло с момента рождения вселенной
1070 лет - время жизни маломассивных черных дыр[59]
1070 калорий - полная энергия запасенная в наблюдаемой вселенной[58]
1080 атомов содержит в себе наблюдаемая вселенная[60]
1085 фотонов - частиц света содержит в себе наблюдаемая вселенная[61]
1090 байт - информация о всем содержимом в наблюдаемой вселенной (на основе данных энтропии)[62]
Для тех, кто еще не до конца научился ориентироваться в логарифмических числах приведу еще пару сравнений. Начнем с числа атомов, всего их содержится в наблюдаемой вселенной около 1080. Но чтобы понять насколько это много, вспомним сколько их содержится в песчинке:
то во сколько раз число атомов, из которых состоит наша планета (1050),
больше числа атомов, из которых состоит крупная песчинка (1020),
во столько же раз число всех атомов, которые содержатся в наблюдаемой вселенной (1080),
больше числа атомов, из которых состоит наша планета (1050).
При этом средняя плотность вселенной очень маленькая и составляет всего примерно один атом на кубический метр[60]. Энергетическая плотность вселенной еще меньше, и ее значение является одной из проблем в физике, но об этом чуть дальше, пока давайте еще сравним энергетические уровни в логарифмических числах:
то во сколько раз энергия выделяемая при сгорании 1 миллиграмма бензина (10 калорий) больше,
чем энергия от одной частицы (фотона) теплового излучения (10-22 калорий),
во столько же вся энергия получаемая Землей от Солнца за год (1024 калорий) больше,
чем энергия выделяемая при сгорании 1 миллиграмма бензина (10 калорий),
во столько же раз энергия взрыва самой мощной сверхновой (1047 калорий) больше,
чем вся энергия получаемая Землей от Солнца за год (1024 калорий),
во столько же раз запасенная в наблюдаемой вселенной энергия (1070 калорий) больше,
чем энергия взрыва самой мощной сверхновой (1047 калорий).
Эти сравнения поражают масштабами, но мы все никак не можем добраться до числа, которое обсудили вначале, и в честь которого называется наука о больших числах. Гугол (10100) - это так много, что не найдется даже такого количества физических объектов в пределах наблюдаемой вселенной, чтобы сравниться с этим числом. Гугол (10100) - это настолько много, что это в квадриллион раз больше чем (1085) число всех элементарных частиц в наблюдаемой вселенной, составляющих как и материю так и излучение. Но мы можем считать не только физические объекты, а еще какие-нибудь другие физические параметры, например, до тепловой смерти вселенной, когда во вселенной не останется ничего кроме излучения и даже черные дыры испаряться, осталось ровно 10100 - гугол лет, такое время жизни самой сверхмассивной черной дыры из известных[59], а это самый долгоживущий объект во вселенной (даже все атомы распадутся намного раньше, чем испарятся черные дыры).
Другое важное число 10123 - настолько сегодня энергетическая плотность энергии вакуума во вселенной слабее, чем в начале большого взрыва[63]. Чем же именно важно это число. Дело в том, что физики посчитали, какой сегодня должна быть энергетическая плотность вакуума (энергия пустого пространства) на основе квантовой теории, и значение, которое они получили, практически совпадает с энергетической плотностью вакуума, такой какой она была в начале большого взрыва, что дает несоответствие с наблюдаемой на 123 порядка (10123). Это называют проблемой нулевой энергии, или "самой большой неточностью в истории физики". До сих пор остается загадкой куда девается энергия вакуума, которая по идее должна порождать непрекращающийся большой взрыв повсюду, а если она погашена или скомпенсирована какими-то квантовыми процессами, то почему не полностью а с такой феноменальной точностью один к 10123. Совпадение это или нет, но максимально возможный объем информации, который может содержать наблюдаемая вселенная, так же примерно равен этому числу: 10123 бит. Если бы в наблюдаемой вселенной содержалось больше информации, тогда она превратилась бы в черную дыру, это число было рассчитано на основе голографического принципа энтропии черных дыр[64].
Что еще мы можем сделать, чтобы получить еще бо́льшие числа в мире материальных вещей, можем посчитать сколько просуществует вселенная до момента тепловой смерти (когда испарится самая тяжелая черная дыра) в планковских единицах времени, мельчайших временных промежутках, и получим 10150. А можем вспомнить про пространственное мышление, когда мы представляли систему из вложенных кубов, и измерить планковскими объемами (планковская длина в кубе) весь объем наблюдаемой вселенной. Давайте сделаем это поэтапно, чтобы наглядно представить доступные измерению масштабы вселенной. Для сравнения так же будем брать общеизвестные измеренные объемы. В качестве примера возьмем типичный холодильник объемом один кубический метр, и в таблице №6.1 прикинем сколько таких холодильников уместилось бы в бо́льшие объемы пространства.
| 101 | совмещенный санузел |
| 102 | вагон метро |
| 103 | общественный бассейн |
| 104 | дирижабль |
| 105 | танкер |
| 106 | египетская пирамида |
| 109 | небольшое озеро (видны берега) |
| 1012 | большое озеро (невидны берега) |
| 1015 | море |
| 1018 | мировой океан |
| 1021 | Земля |
| 1024 | Юпитер |
| 1027 | Солнце |
| 1036 | самая большая звезда |
| 1045 | небольшая туманность |
| 1054 | звездное скопление |
| 1061 | наша галактика (Млечный путь) |
| 1068 | скопление галактик |
| 1072 | сверхскопление галактик |
| 1081 | наблюдаемая вселенная |
Теперь поступим наоборот, и в таблице №6.2 посчитаем сколько бы меньших объемов пространства уместилось бы в одном таком холодильнике.
| 103 | бутылка молока |
| 106 | чайная ложка |
| 108 | рисовое зернышко |
| 1011 | песчинка |
| 1016 | человеческая клетка |
| 1018 | бактерия |
| 1020 | вирус |
| 1029 | атом |
| 1045 | протон |
| 10105 | планковский объем |
Ну а дальше, используя алгебру уровня седьмого класса, нетрудно посчитать, сколько же планковских объемов уместится внутрь наблюдаемой вселенной:
одна колода карт:
две колоды карт:
три колоды карт:
Есть еще одно намного бо́льшее число, которое могло бы иметь физический смысл, и происходит оно из теории струн. Эта теория пытается объяснить единство происхождения всех фундаментальных сил и элементарных частиц. Согласно ей все элементарные частицы - это вибрирующие нити чистой энергии вакуума (струны), размером с планковскую длину, а само наше пространство имеет больше трех измерений, но остальные нами ненаблюдаемы, потому что свернуты на тех же сверхмалых планковских масштабах. Вибрации, что создают струны собственно и определяют все свойства частиц и фундаментальных сил, а колеблются они именно таким образом, потому что по другому не могут, из-за того что остальные измерения свернуты. Теория очень популярна среди физиков-теоретиков, но пока имеет гипотетическую природу. Эта теория делает интересное предсказание о том, что те вибрации, которые издают струны не единственные, которые возможны в рамках этой теории. То есть та конфигурация вакуума, что заставляет их колебаться, создавая именно ту симфонию, которой и является наша вселенная, это не единственная возможность свернутости измерений. Оказывается дополнительные ненаблюдаемые измерения, которые предсказывает теория, можно свернуть несколькими способами, каждый из которых будет заставлять колебаться струны по-разному. По последним подсчетам физиков-теоретиков[65] таких возможностей для свертывания дополнительных измерений, что формируют свойства вакуума, насчитывается около 10272000 (число у которого после единицы 272000 нулей). Почему именно такая конфигурация вакуума досталась нам, что в ней могут обитать разумные существа, ведь вероятность, что она окажется такой была один к 10272000 - это один из самых больших неразрешенных вопросов теории струн. Чтобы превзойти это число, используя комбинаторику на карточных картах, нам потребуется замешать 1200 полных колод по 52 карты в каждой, и только тогда количество возможных вариантов последовательности карт будет больше. Тем не менее этому числу все еще можно дать название в американской системе именования больших чисел. Давайте ради забавы сделаем это, только возьмем немного другое число, потому что как вы заметили 10272000 - это не просто округленное число, а логарифмически округленное число, то есть у него округлен даже показатель степени. Мы же возьмем какое-нибудь логарифмически точное число, например 10272136 . Итак, сначала разделим показатель на 3, и получим 272136/3 = 90712, разобьем это число на разряды: 90 тысяч 712. Теперь обратимся к таблице №2 и, воспользовавшись правилами именования, по частям соберем название, должно получиться: нонаджинти-миллини-дуо-деци-септиджинти-ллион.
Но мы всё топчемся на месте, думаю, что вы уже готовы к настоящему прыжку. Давайте возьмем число, которое кардинально больше, чем гугол, такое что с его названием не справится даже американская система именования больших чисел. Представляю вам
Начнем с теории космической инфляции, которая не раз уже упоминалась. Она пока еще не считается строго доказанной, но на сегодняшний день это лучшая теория, которая наиболее детально, и согласуясь с наблюдениями, объясняет как именно происходил большой взрыв. Согласно этой теории в самые первые мгновения наш космос невероятно или, говоря языком теории, инфляционно увеличился в размерах, этот краткий миг экспоненциального расширения и был собственно тем самым большим взрывом, породившим космос. Мы не наблюдаем кривизны пространства на больших масштабах именно из-за того что в прошлом вселенная испытала стадию инфляционного расширения, из-за которой она стала очень очень большой, намного больше наблюдаемой нами области, такой что все возможные искривления пространства распрямились. Стадия инфляционного расширения вселенной отличалась от современной стадии расширения вселенной не только тем, что она была экспоненциально быстрее, но и тем, что это было расширение с сохранением плотности. Такое было возможно, потому что первичный вакуум, из которого зародилась вселенная был настолько высокоэнергетичным, что обладал высоким отрицательным давлением, и по закону Эйнштейна гравитация должна была наоборот его расталкивать. Однако отрицательное давление окружающей среды было настолько высоко, что после расширения высвобожденная энергия по той же формуле Эйнштейна порождала примерно столько же примерно такого же высокоэнергетичного вакуума и процесс продолжался (на самом деле местами его было чуть меньше, поэтому космическая инфляция все-таки остановилась). В этом процессе не было никакого нарушения закона сохранения энергии, положительная энергия порождаемой материи полностью компенсировалась отрицательной энергией накапливаемой в гравитационном поле, так что их сумма всегда в итоге была равна нулю, поэтому в соответствии с теорией космической инфляции для рождения вселенной энергии вовсе и не требовалось, фактически она появилась из ничего[53]. Ну хорошо, если теория космической инфляции так детально описывает рождение и начальное расширение всей вселенной, тогда она должна дать ответ на вопрос каковы же ее истинные размеры (имеется ввиду всей вселенной, а не только о наблюдаемой области). И теория дает ответ на этот вопрос. Однако это очень странный ответ, особенно для тех кто не знаком с теорией относительности. Теория космической инфляции утверждает, что наша вселенная бесконечна и безгранична, но имеет конечный объем независящий от систем отчета, который можно рассчитать в определенный момент времени. И конечно же тут необходимы пояснения, так что мне придется отвлечься от основной темы повествования, чтобы объяснить это.
Во-первых следует сказать, что инфляционное расширение не могло остановиться везде одновременно. И вот тут начинается самое странное. Из теории следует, что в нашей области пространства инфляционное расширение остановилось немного раньше чем соседних областях, а в тех немного раньше чем окружающих их областях. Однако одновременность в масштабах вселенной понятие относительное, и к такому же выводу пришли бы обитатели соседних областей, что инфляция сначала остановилась в их области, и только чуть позже в нашей. Действительно, согласно теории относительности Эйнштейна два наблюдателя находящихся на больших расстояниях и удаляющихся друг от друга будут иметь собственные представления об одновременности и каждый в своей системе отчета будет прав. Так или иначе каждый наблюдатель в нашей вселенной, построит для себя собственную инфляционную модель вселенной, в которой в его области пространства инфляционное расширение остановилась раньше чем в других, а где-то совсем далеко инфляционное расширение все еще продолжается, то есть там все еще происходит большой взрыв. Таким образом он придет к выводу что все пространство имеющееся во вселенной находится в конечном объеме, и где-то очень далеко оно еще не родилось, но будет продолжать рождаться вечно. Однако к такому выводу придет только наблюдатель изучающий историю вселенной, а наблюдатель который просто взглянет в глубину космического пространства, а следовательно и в глубину времени (увидев там прошлое, ибо информация обо всем во вселенной не может двигаться быстрее скорости света), придет к выводу что инфляция повсюду закончилась одновременно, продлившись всего одну 10-35-ную долю секунды, и следовательно большой взрыв произошел в определенный момент, породив сразу всю вселенную целиком, и для него наша вселенная будет бесконечной, то есть таковой родившаяся. Таким образом, с одной стороны мы имеем бесконечность времени, в течение которого вселенная продолжит где-то далеко рождаться, полученную наблюдателем изучающим историю зарождения вселенной, однако он в своих выводах придет к тому что вселенная имеет конечный объем. С другой стороны мы имеем бесконечность пространства, к которой пришел наблюдатель изучая окружающий космос, однако он постановил что вся вселенная родилась одновременно и имеет однозначный и определенный возраст. Так теория относительности превращает бесконечность времени одного наблюдателя в бесконечность пространства другого наблюдателя. Вот поэтому для всех наблюдателей в их собственных системах отчета вселенная всегда будет бесконечной, но если бы мы могли как-то со стороны посмотреть на вселенную, то пришли бы к выводу что она занимает конечный объем, но при этом все еще продолжает рождаться[64]. Теория космической инфляции позволяет нам рассчитать этот объем, и что интересно каждый наблюдатель во вселенной спустя 13,8 миллиарда лет после рождения его наблюдаемой области вселенной, так же как и мы, будет считать что именно его область пространства первая вышла из стадии инфляционного расширения (и будет прав в рамках своей системы отчета), однако в своих расчетах все они получат один и тот же "объем вселенной, если бы на нее можно было посмотреть со стороны". Диаметр этого объема по теории космической инфляции составляет около 101000000000000 = 101012метров - число с триллионом нулей[66]. Это столь большое число, что для написания всех его нулей в десятичной записи необходимо чтобы 1000 человек одновременно писали эти нули в течении 30 лет, при этом написанные вплотную друг к другу нули покрыли бы площадь всей ВДНХ в Москве.
Во сколько же раз тогда получается вся вселенная больше наблюдаемой нами области? Учитывая полученное число, этот вопрос задан не совсем корректно, даже вопрос "на сколько порядков она больше" - не даст полного понимания ее масштаба. Давайте так, представьте себе стадион, а теперь возьмем всю наблюдаемую вселенную и уменьшим ее в диаметре до размеров стадиона, а потом снова возьмем наблюдаемую вселенную и уменьшим ее диаметр до размеров стадиона и т.д. Вспоминайте упражнение с вложенными кубами и подключайте пространственное мышление, только теперь уровень сжатия стал сильнее, мы сжимаем диаметр не в 10 раз а в 1025 раз. Короче говоря, повторять упражнение по сжатию вселенной до размера стадиона, а потом снова и снова, нужно 40 миллиардов раз, и только тогда мы можем сопоставить размеры стадиона и всей вселенной из предсказаний теории космической инфляции. Если бы после каждого такого мысленного сжатия мы бы рисовали палочку, наподобие той что из рисунка №2, где мы из палочек составляли тысячу, то из этих палочек, так же плотно рисуя их друг к другу, получилась бы строка длиной с земной экватор. Что же, истинные масштабы мироздания могут повергнуть в шок неподготовленных.
Если у вас все равно не получилось представить истинные размеры вселенной, то не переживайте, на самом деле без использования каких-либо аналогий это практически никому не под силу, потому что здесь мы уже почти подошли к максимально возможному числу, которое теоретически с произвольной точностью может быть осознано человеком. Исследователи установили, что типичный человеческий мозг может за всю жизнь усвоить около одного петабайта информации, или переводя в биты получим 10 квадриллионов (1016) бит[67]. И речь идет не о размере всех сериалов, закодированных в цифровом виде, которые вы посмотрели, а о понятиях и концепциях, которые сформировали у себя в голове. То есть это размер вашего внутреннего контента. Хочется отметить, что мы достаточно быстро усваиваем информацию, тогда как средняя продолжительность жизни человека не превышает 3 миллиардов секунд (3×109), получается что средняя скорость, с которой данные накапливаются в нашем мозге, составляет около 3 мегабит в секунду, почти как у вашего домашнего интернета (если вы конечно не читаете эту книгу спустя 10 лет после ее написания, тогда вероятно ваш домашний интернет будет намного быстрее). Представим что вся эта информация превращается в цифры некого числа. Вспомните таблицу №5, и тогда поймете что максимально возможное число, которое вы теоретически можете представить себе с произвольной точностью будет соизмеримо с 21016, или, иными словами вы сможете назвать любую цифру в записи этого числа. Легко посчитать сколько же цифр будет у этого числа (21016 ≈ 103×1015), и получается немного немало - 3 квадриллиона (3×1015). Конечно, в реальности ни один человек не может перенаправить поток воспринимаемой и запоминаемой информации, получаемой в течение жизни, в представление какого-либо набора цифр, тут мы просто изучили предел его возможностей. Интересно, что система для записи сверхбольших чисел, которую разработал Архимед в своей книге Псаммит "Исчисление песчинок", где пытался измерить размер вселенной песчинками, и назвал мириадной нотацией, еще позволяет записать это число. Возможности его мириадной нотации были ограничены числом, у которого в нашей десятичной нотации после 1 содержится 80 квадриллионов (8×1016) нулей[68].
Стоит отметить, что раз 21016 ≈ 103×1015, то может показаться что это число очень близко по размеру к 101016. Но на самом деле 101016 больше 103×1015 в 107×1015 раз. Дальше мы подробнее разберем почему так получается, но вот расчеты, если вам это интересно прямо сейчас: 101016/103×1015 = 10(1016-3×1015) = 107×1015. То есть, число, которое показывает во сколько раз 101016 больше 103×1015, само по себе больше чем число 103×1015. Настолько большие эти числа, что при их сравнении интуиция нас подводит. Все же, с вашего позволения, я округлю 21016 ≈ 101016, чтобы его удобнее было сравнивать с другими числами, и буду так поступать впредь, потому что такие трехэтажные числа для нашего понимания столь велики, что когда мы увеличиваем основание степени этих чисел, это совсем незначительно сказывается на их верхнем показателе степени. Вообще такой многоэтажный способ записи больших чисел, уже не является логарифмической нотацией, он называется степенные башни, и стоит держать в голове, что главное в степенных башнях это их высота и значение самого верхнего показателя, так 22100 будет больше чем 1001002, и даже больше чем 101020, но меньше чем 22210. Поэтому при округлении таких чисел обычно принято сводить степенную башню к тому, чтобы на каждом этаже кроме последнего была десятка. Потому что именно высота башни делает устойчивым значение ее самого верхнего показателя, и чем башня выше тем сложнее его изменить, чтобы мы с ней ни делали. Так например, чтобы изменить показатель двухэтажной башни достаточно умножить ее на число равное основанию: 1011 = 10×1010. Чтобы изменить верхний показатель трехэтажной башни ее необходимо уже возвести в степень равную второму этажу, например 101011 = (101010)10. А чтобы изменить верхний показатель четырехэтажной башни, тот тут уже придется воспользоваться тяжелой артиллерией: нужно возвести данную башню в степень равную всем ее верхним этажам кроме первого и сделать это столько раз, сколько по размеру третий этаж, например (10101011) = (((((((((((10101010)101010)101010)101010)101010)101010)101010)101010)101010)101010).
И чтобы убедиться насколько большие числа создают степенные башни, давайте сразу проверим насколько максимально возможное число, которое теоретически с абсолютной точностью мог бы представить человек, больше чем диаметр всей вселенной, который мы бы измерили если бы смогли посмотреть на нее снаружи. Если вам кажется, что прежде мы должны определиться с единицами измерения диаметра, то в действительности это не имеет большого значения. Пусть в метрах этот диаметр составляет 101012, тогда если мы переведем его в планковские единицы длины, то получим: 101012/1035 = 101000000000000/1035 = 101000000000000-35 = 10999999999965 ≈ 101012. Что касается сравнения этих двух чисел 101016 и 101012 , то тут так же следует быть очень внимательным, ибо это уже степенные башни, а не обычные логарифмические числа, у которых можно было вычесть верхние показатели как в классическом примере из алгебры седьмого класса (например, 1016/1012 = 1016-12 = 104 - одно число больше другого в 10000 раз). Этим же двум числам перед сравнением не мешало бы поставить скобочки в показателях: 10(1016) и 10(1012), тогда правильно считать надо так: 10(1016)/10(1012) = 10(1016-1012) = 101000000000000000-1000000000000 = 10999000000000000 ≈ 101016 - получается, что одно число больше другого практически во столько же раз, что и масштаб самого этого числа. Можно еще попробовать объяснить сравнительные масштабы двух этих чисел на примере вложенных кубов из рисунка №11. Для создания числа 101012 - необходимо представить рисунок из более чем 300 миллиардов вложенных кубов, а для создания числа 101016 - необходимо представить рисунок из более чем 3 триллионов вложенных кубов.
Дальше я приведу число, которое является расстоянием, бо́льшим чем размер всей вселенной на текущий момент времени, высчитанный теорией космической инфляции, и надо объяснить почему это расстояние все равно имеет смысл. Ну во-первых конечный размер всей вселенной можно определить только если мы как бы смотрим на ее со стороны, но ведь в реальности на вселенную нельзя посмотреть со стороны. Гипотетический наблюдатель находящийся за пределами вселенной, действительно определил бы, что на текущий момент вселенная продолжает рождаться, останавливая космическую инфляцию на своих границах, и тот объем пространства, что уже родился будет для него конечным. Но реальные наблюдатели всегда находятся внутри вселенной и для них этот конечный объем - является временем, что прошло с момента рождения вселенной. Однако по своей системе отчета живут они в бесконечном пространстве, и это их бесконечное пространство - для того гипотетического наблюдателя является бесконечным потенциальным временем, что вселенная продолжит рождаться в будущем. Теория относительности превращает его пространство в наше время и наоборот. Поэтому для реальной системы отчета находящейся внутри вселенной любые расстояния вполне правомерны, ведь в такой системе отчета пространство бесконечно[64].
Однако несмотря на то, что для нас вселенная бесконечна, квантовая механика позволяет организовать материю конечным числом способов, значит по статистике где-то далеко-далеко-далеко должна быть полная копия нашей планеты, где копия вас читает эти строки написанные копией меня. Ученые посчитали это расстояние (на самом деле это несложно, рассчитываем энтропию всей нашей планеты до квантового уровня, выражаем это число в виде количества байт информации и средствами комбинаторики, просчитываем число всех возможных конфигураций). Оно приблизительно равно 101028 метров - число с 10 октиллионом нулей[53]. Еще на таком же расстоянии, дальше или с другой стороны, будет другая копия планеты, и так далее, повсюду мироздание окажется самоподобным, как гигантский математический фрактал. На расстояниях чуть ближе могут встречаться и неполные копии, а с небольшими изменениями, где, например, я так и не взялся за написание этой книги. Чтобы почувствовать масштаб этого числа в десятичной записи, приведу очень интересную аналогию. По приблизительным подсчетам астрономов в нашей галактике около 10 миллиардов планет потенциально похожих на Землю, это больше чем сегодня людей проживает на нашей планете. Представим себе отдаленное будущее, в котором человечество колонизировало всю галактику, создав колонии на каждой их этих планет. Допустим численность населения каждой из таких колоний примерно соответствует численности населения современной Земли, тогда если каждый человек в течении пяти лет будет писать нули, то мы получим необходимое число нулей для записи числа 101028 в десятичной нотации, при этом в результате данного мысленного эксперимента вся поверхность этих планет будет полностью исписана нулями, вплотную прилегающими друг к другу. Если же для визуализации мы используем аналогию с вложенными кубами из рисунка №11, то тогда для создания числа 101028 - необходимо представить рисунок из более чем 3 октиллионов вложенных кубов, то есть эти вложенные кубы пришлось бы рисовать до самых границ наблюдаемой вселенной. Во сколько же 101028 раз больше предыдущего числа 101016? И вы уже должны понимать, что тут больше неприменимы такие слова как "во сколько раз", или даже "на сколько порядков". Можно сказать, что "порядок порядка числа" отличается в триллион раз, но это не особо вносит ясности в понимание сравнительного масштаба чисел. Степенные башни похоже окончательно убивают интуитивное понимание масштаба, поэтому дальше уже не будет сравнений, поскольку привычные сравнения на этом этапе уже не помогут, и читателю остается уповать лишь на силу собственного абстрактного понимания чисел.
Ну а мы идем дальше в попытках дотянуться до гуголплекса. После тепловой смерти вселенной все же будут происходить квантовые скачки, это такие события квантовой природы, которые способны спонтанно создавать какие-либо структуры. Такое событие надо сказать очень редкое, вряд ли стоить ожидать крупного квантового скачка до наступления тепловой смерти, а вот после у них будет предостаточно времени, чтобы проявить себя. Вопрос стоит таким образом, сколько должно пройти времени, чтобы квантовый скачок спонтанно создал такую структуру, которая бы могла разумно мыслить и думать то, что она человек, вроде меня или вас, ее еще называют Больцмановский мозг в честь физика основателя термодинамики предсказавшего тепловую смерть вселенной. Ученые посчитали и это. Такое может произойти через 101069 лет[69]. Сама возможность этого немного пугает, ведь это значит, что наше сознание на самом деле может оказаться сознанием такого Больцмановского мозга и вся окружающая реальность это лишь его вымысел. Сложно назвать такие вычисления физическими, многие сочтут это уже метафизикой или даже философией, особенно потому что количество нулей после единицы у данного числа столь велико, что если бы мы могли клонировать сколько угодно людей, только для того чтобы они записали эти нули, то для того чтобы прокормить их всех нам потребовалось бы столько пищевой энергетической ценности сколько энергии содержится во всей наблюдаемой вселенной. Но так или иначе нам опять не хватило до гуголплекса.
Так давайте же тогда детально разберем, что же такое гуголплекс (1010100). У этого числа гугол нулей. И как вы понимаете, я не смогу записать его в строку, более того, даже если бы я мог нарисовать ноль на каждой элементарной частице в пределах наблюдаемой вселенной, мне бы просто не хватило частиц, чтобы это сделать. То есть, это число вообще невозможно отобразить в десятичной записи. Числа такого масштаба как гуголплекс уже полностью лишают нас возможности их точного выражения. В то время как, используя десятичную нотацию, я в принципе могу записать любое число, скажем, в диапазоне от гугола до десяти гуголов, мне нужно просто подобрать 100 цифр. То есть, я не могу, конечно, перечислить все числа в этом диапазоне, но могу записать любое произвольное число с абсолютной точностью. Но, к сожалению, у меня нет возможности, абсолютно точно записать любое произвольное число в диапазоне от гуголплекса до десяти гуголплексов, поскольку в этом случае я уже не смогу поменять любую цифру в десятичной записи гуголплекса, ибо этих цифр у него целый гугол, и я не смогу записать их все в десятичной нотации, и как мы выяснили я даже представить их не смогу, потому что мозг физически не может представить больше квадриллиона конкретных цифр. А это приводит к еще одному удивительному выводу об этом числе. Как вы могли понять из таблицы №5, любая информация закодированная в двоичном коде может быть выражена как некое натуральное число, ну потому что двоичный код можно интерпретировать как двоичную систему счисления, и мы уже разбирали это, когда говорили о максимальном произвольно точном числе, которое может представить человек. Так вот учитывая, что информационное содержимое наблюдаемой вселенной составляет не более чем 1090 байт, получается что вся информация, которая есть в нашей вселенной, может быть представлена как некое натуральное число соизмеримое с 21090 (так же можем округлить, чуть в большую строну до 101090), которое будет меньше чем гуголплекс.
Может быть нас спасет комбинаторика? Колоду из скольких карт нужно взять и перемешать, чтобы мы потенциально могли получить больше гуголплекса вариантов последовательности карт внутри нее? Такая колода должна содержать 10100 гугол карт, да и то число возможных последовательностей будет приблизительно 1010102, ни о каком кардинальном превосходстве не может быть и речи. Это еще раз показывает насколько велики числа, до которых мы добрались.
Давайте попробуем применить комбинаторику ко всей наблюдаемой вселенной. Как я и говорил выше, квантовая механика позволяет организовать вещество во вселенной конечным количеством способов. И есть способ подсчитать количество возможных состояний, в которых могла бы находится наша вселенная. В соответствии с голографическим принципом, согласно которому физические состояния в объеме можно закодировать на площади ограничивающий этот объем, полная квантовая энтропия области рассчитывается как булеан количества планковских площадей входящих в сферу. А теперь простыми словами объясню как это можно рассчитать. Сперва надо посчитать максимально-возможный объем информации, которым располагает наша наблюдаемая вселенная, он как раз в соответствии с голографическим принципом будет равен числу планковских площадей, которыми можно выложить условную сферу диаметром с нашу наблюдаемую вселенную, и я уже приводил это число выше оно равно 10123 бит. Хочу заметить, что это число будет намного больше числа 1090 бит, которое показывает сколько сейчас содержится информации в наблюдаемой вселенной, ведь мы говорим о максимальном потенциально-возможном объеме информации, который может содержатся в наблюдаемой вселенной. Как показывает голографический принцип если превысить этот информационный объем объект должен превратиться в черную дыру. Ну а чтобы подсчитать все возможные состояния, в которых теоретически может находиться область пространства размером с наблюдаемую вселенную, нужно просто снова обратится к таблице №5, и понять что число таких состояний равно максимальному натуральному числу, которое можно закодировать в максимально-возможном объеме информации (10123 бит), которым располагает наша наблюдаемая вселенная. Так мы и получим 210123, которое я опять же для простоты округлю до 1010123. Для более наглядной аналогии данного масштаба, представим, что у нас есть очень много маленьких игральных карт, каждая из которых имеет лишь планковскую длину в диаметре, вопрос ставится следующим образом: сколько возможных комбинаций из этих карт можно составить, если выложить их плотно друг другу, так чтобы они покрывали область равную всей видимой вселенной. Для области размером с наблюдаемую вселенную так же получается число примерно равное 1010123, значит где-то далеко в нашей бесконечной вселенной (всей, не только наблюдаемой) по теории вероятности на таком расстоянии (и уже как вы понимаете, неважно чего, метров, километров или световых лет) должна находится точно такая же область пространства как наша наблюдаемая вселенная. Это будет абсолютная копия без каких-либо отличий вплоть до планковских масштабов[64].
Есть ли какое-либо физическое число, которое кардинально переплюнет гуголплекс. Вполне возможно, что такое число существует. Сегодня космологи, изучающие большой взрыв, создавший нашу вселенную, склоняются к тому, что большой взрыв создал не только нашу вселенную, но и великое множество параллельных вселенных существующих в своем собственном пространстве-времени и имеющие собственные законы физики. Это одно из возможных следствий теории космической инфляции. Дело в том, что гиперраздувание пространства во время стадии космической инфляции должно происходить на фоне неравномерно кипящего высокоэнергетичного вакуума, в котором вполне возможно могут образоваться независимые вселенные. Чтобы понять как это происходит нам снова необходимо попытаться посмотреть на нашу вселенную "снаружи", а как мы помним в соответствии с теорией космической инфляции при взгляде "снаружи" мы должны воспринимать вселенную как конечный объем, границы которого продолжают инфляционно расширятся, а на краях инфляция останавливается порождая новые области вселенной. С такой точки зрения инфляция полностью не остановится никогда и будет продолжаться вечно. Однако поскольку двигатель инфляции это первородный кипящий высокоэнергетичный вакуум, испытывающий квантовые колебания, то следовательно космическая инфляция должна была начать останавливаться не только в разные моменты для соседних областей, но и одновременно в разных совершенно несвязанных областях[53]. Напомню, что все разумные обитатели вселенной, изучая процесс космической инфляции решат что именно в их области инфляция остановилась раньше, но зная теорию относительности, поймут что обитатели соседних областей решат так же, а экспериментальные наблюдения вообще покажут что инфляция остановилась везде одновременно. Но если эти разумные обитатели кроме теории относительности учтут еще и квантовые колебания, то они так же должны прийти к выводу, что случайные колебания плотности первородного вакуума должны были начать процесс остановки инфляции независимо в разных областях, причем границы этих областей будут по-прежнему инфляционно расширятся относительно друг друга, и между ними так же могут формироваться новые области остановки инфляции. Этот процесс немного похож на формирование пузырей при кипении воды, вот почему вселенные порождаемые космической инфляцией иногда называют пузырями. Получается, что с учетом квантовой механики наш взгляд на вселенную "снаружи" должен показать нам, что вселенная разделена на независимые области, соответственно так же имеющие в каждый определенный момент времени конечные объемы, за границами которых инфляция продолжается, а на их границах порождаются новые области пространства[64]. А что же покажет точка отчета изнутри? Да все тоже самое, как если бы мы не учитывали квантовые колебания в начале процессе инфляции, эти другие отделенные объемы пространства никогда и никак не будут наблюдаемы изнутри. Даже в соответствии с теорией относительности точки отчета взятые в этих независимых объемах нельзя объединить в единую систему отчета, физики обычно называют это причинным разделением. Значит эти разделенные области пространства следует считать параллельными вселенными, наблюдателю в каждой из которых будет казаться что его вселенная возникла одномоментно будучи сразу бесконечной и следовательно для его системы отчета другие параллельные вселенные будут лежать за пределами бесконечности (как бы дико это не звучало).
Но теория космической инфляции на этом не останавливается, она предсказывает что другие вселенные рождаются не только "снаружи" нашей вселенной, но так же они должны рождаться и внутри нашей вселенной. К таким предсказаниям можно прийти если связать теорию космической инфляции с теорией струн. Вспомним, что квантовая пена пространства-времени, которая по теоретическим расчетам существует на планковских масштабах в нашей вселенной, сама по себе является кипящим высокоэнергетичным вакуумом. Вот и ответ на вопрос, куда девается гигантская плотность энергии, которая по расчетам квантовой механики должна быть запасена в пустом вакууме, она расходуется на постоянное создание вселенных. То есть космическая инфляция в порождаемых ею вселенных не то что бы останавливается, а скорее переходит внутрь. Это происходит следующем образом, в результате случайного квантового колебания кусок пространства планковских размеров отрывается от нашей вселенной и, полностью отделившись, сразу же под воздействием гигантской плотности энергии, что была заключена в вакууме, начинает инфляционно раздуваться в свое собственное пространство-время. Это инфляционное расширение вечно и неоднородно, местами оно останавливается формируя независимые вселенные по вышеописанному сценарию. Такие понятия как вечность и бесконечность здесь так же меняются местами. Родившиеся внутри вселенные могут восприниматься изнутри как имеющие бесконечное пространство и свое одномоментное рождение в прошлом, а снаружи как конечное пространство, но при этом бесконечно рождающееся из инфляционного расширяющегося вакуума, который в целом так же имеет конечный объем. Термины "внутри" и "снаружи" не определяют никакой границы, просто бесконечность пространства не позволит покинуть вселенную и посмотреть на нее снаружи, так же как и нет возможности проникнуть внутрь пузырька квантовой пены, в котором в свое собственное пространство вечно рождаются новые вселенные. Интересно то, что вся эта инфляционно расширяющаяся процессия, которая рождает внутри себя бесконечные, по их собственным системам отчета, вселенные, при взгляде "снаружи" в определенный момент времени не только будет иметь конечный объем каждой отдельно взятой родившейся внутри вселенной, но и в целом, будучи когда-то маленьким планковским пузырьком, так же в любой определенный момент времени будет иметь конечный объем, являясь замкнутой многомерной сферой, пусть и экстремально расширяющейся[70]. Однако ни один наблюдатель находясь внутри любой из родившихся вселенных не сможет рассчитать объем всего, некогда отделившегося от другой вселенной и ныне породившего их, инфляционного пространства. Проблемой для расчета будет относительность, ведь объем своей "вселенной снаружи из инфляционного пространства" он считал относительно момента остановки инфляции в этой своей вселенной, однако для него, в прямом смысле слова, никогда не существовало момента, когда все инфляционное пространства отделилось от другой вселенной.
Если принять на вооружение такую картину мира, то тут же появляется ответ на вопрос почему нашей вселенной достался один из 10272000 вариантов конфигурации вакуума, от которого зависят свойства элементарных частиц и фундаментальных сил, и почему эта конфигурация вакуума гасит свою внутреннюю плотность энергии с такой точностью один к 10123, сохраняя вакуум в стабильном состоянии и перенаправляя его потенциал на создание других вселенных. Ответ в том, что число видов этих параллельных вселенных непостижимо велико и в каждой из них будут свои законы физики, своя конфигурация вакуума (скученность дополнительных измерений пространства для колебания струн), свой собственный уровень стабильности вакуума и способность к порождению других вселенных. Неудивительно что нашей вселенной досталась именно такая конфигурация вакуума, в которой возможно существование разумных существ, иначе некому было бы об этом рассуждать. Вполне возможно, что несмотря на разнообразие вариантов конфигураций вакуума и вариантов событий, которые могут произойти в параллельных вселенных, многие из них будут полными копиями друг друга. Весь этот разрастающийся фрактал из параллельных вселенных иногда называют мультивселенной. Картина мультивселенной описываемая космической инфляцией, показывает нам, что большое и малое это единое целое, и делает из нашего мироздания решето, вечно порождающее миры. Задумайтесь только, ведь квантовая пена это просто пространство на ультрамикроскопическом масштабе, она повсюду, вокруг нас и внутри нас, значит прямо сейчас рядом с вами и внутри вас рождаются вселенные, в которых происходит тоже самое. Наш островок стабильности в этом безумном мире, "наружный" объем которого на текущий момент по приблизительным подсчетам равен 101012, в рамках теории принято называть инфляционным доменом, получается что другие инфляционные домены должны быть параллельными вселенными в том смысле, в котором принято использовать это выражение. Инфляционные домены находящиеся в одном инфляционно расширяющемся пространстве будут иметь немного отличающиеся законы физики, а те которые находятся в разных расширяющихся пространствах, отделившихся друг от друга будут иметь сильно отличающиеся законы физики, вплоть до разного числа пространственных измерений. Даже если этот сплав теории космической инфляции и теории струн окажется неудачным и найдется другое объяснение, того как погашена плотность энергии нашего вакуума (и окажется, что в нем не рождаются новые миры) все равно квантовая механика допускает вероятность того, что пространство нашей вселенной снова может перейти в стадию инфляции, которая вновь начнет порождать миры, эта вероятность очень мала, и далее мы ее еще рассмотрим, но поскольку в своей системе отчета вселенные могут существовать бесконечно долго, то рано или поздно это должно произойти.
Получается, что общее количество существующих инфляционных доменов бесконечно, или, говоря иначе, мультивсленная содержит бесконечное число параллельных вселенных бесконечно порождающих самих себя, то есть является бесконечной как в пространстве так и во времени. Но вот некоторые инфляционные домены могут получаться абсолютно одинаковыми, вплоть до каждого планковского объема, поскольку, как мы помним, квантовая механика позволяет организовать материю конечным числом способов. То есть получается, что число различающихся инфляционных доменов (параллельных вселенных) конечно, и теория космической инфляции позволяет оценить размер этого числа, для этого просто необходимо посчитать энтропию всех возможных инфляционных колебаний плотности, которые в итоге и ведут к остановке инфляции. Теоретики пришли к выводу что космическая инфляция способна породить 101010000000 вселенных[67]. Это число столь велико, что для его более краткой записи нам необходимо ввести четвертый уровень степенной башни: 101010000000 = 1010107. Такое количество различающихся вселенных непостижимо, и оно намного, намного, намного, намного больше чем гуголплекс. Но самое главное для нашего здравого смыла, что если теория о параллельных вселенных верна, то она частично опровергает гипотезу Больцмановского мозга. Потому что, учитывая количество возможных вселенных, куда более вероятно, что мы окажемся в реальной вселенной, чем в воображении спонтанно возникшего Больцмановского мозга. Так же, учитывая такое число вселенных, можно быть смело уверенным, что где-то среди них будет много вселенных похожих на нашу, в которых реализуется одна из 10272000 возможных конфигураций вакуума, и где плотность энергии вакуума будет скомпенсирована с точностью 1 к 10123, поскольку оба этих числа ничтожно малы по сравнению с 1010107. Кроме того исследователи отмечают, что человечество не сможет полностью изучить и осознать все возможные виды существующих вселенных, поскольку отдельно взятый человек не может осознать более 1016 битов информации, что дает примерно 101016 видов хранения информации, а как мы выяснили, это очень большое число, и даже если мы умножим его на 7 миллиардов людей, его самый верхний показатель степени не изменится, но все же оно так же ничтожно мало по сравнению с 1010107.
Некоторые физики еще сильнее расширяют понятие мультивселенной, включая в него не только инфляционные домены возникающие в процессе вечной инфляции, но и многомировую интерпретацию квантовой механики, согласно которой все квантовые вероятности реализуются, но в разных измерениях, и это не привычные нам пространственные измерения, а гильбертовы вероятностные измерения, число которых бесконечно. То есть любое, даже самое маловероятное, но не противоречащее законам физики событие уже произошло только в параллельном гильбертовом измерении[64]. Тогда получается мультивселенная бесконечна не только во временном и пространственных измерениях, но так же и в измерениях "а что если все было бы иначе". Ну а бесконечность не измеришь никаким числом. Но раз уж мы заговорили о вероятностях, то числа в вероятностях некоторых физических явлений, которые допускает квантовая механика, могли бы переплюнуть даже число возможных видов инфляционных доменов. Давайте постепенно доберемся до этих чисел, для этого я сделал Таблицу №7, в которой собрал несколько вероятностей в порядке уменьшения их шанса, а следовательно увеличения числа в знаменателе вероятности.
| событие | с шансом 1 из ... |
| вероятность выпадения орла при броске монетки | 2 |
| вероятность получить "пару" в пятикарточном покере (округл.) | 2 |
| вероятность выпадения "шестерки" на игральной кости | 6 |
| вероятность угадать 1 цифру | 10 = 101 |
| вероятность получить "две пары" в пятикарточном покере (округл.) | 20 |
| вероятность получить "сет" в пятикарточном покере (округл.) | 50 |
| вероятность рождения двойни[71] | 80 |
| вероятность угадать 2 цифры | 100 = 102 |
| вероятность получить "стрит" в пятикарточном покере (округл.) | 250 |
| вероятность получить "флеш" в пятикарточном покере (округл.) | 500 |
| вероятность получить "фулл хаус" в пятикарточном покере (округл.) | 700 |
| вероятность угадать 3 цифры | 1 000 = 103 |
| вероятность выпадения орла 10 раз подряд при бросках монетки (округл.) | 1 000 |
| вероятность погибнуть в автокатастрофе[72] | 3 500 |
| вероятность получить "каре" в пятикарточном покере (округл.) | 4 000 |
| вероятность того что подброшенная монетка встанет на ребро[73] | 6 000 |
| вероятность рождения тройни[71] | 6 400 |
| вероятность угадать 4 цифры | 10 000 = 104 |
| вероятность найти четырехлистный клевер[74] | 10 000 |
| вероятность столкновения астероида с землей (с энергией удара 1 гигатонна) в ближайшие 10 лет[75] | 62 000 |
| вероятность получить "стрит-флеш" в пятикарточном покере (округл.) | 72 000 |
| вероятность угадать 5 цифр | 100 000 = 105 |
| вероятность рождения четверни (округл.)[71] | 510 000 |
| вероятность получить "роял-флеш" в пятикарточном покере (округл.) | 650 000 |
| вероятность угадать 6 цифр | 1 000 000 = 106 |
| вероятность родится в семье миллиардера[27] | 3 500 000 |
| вероятность дожить до 110 лет[76] | 7 000 000 |
| вероятность погибнуть в авиакатастрофе[77] | 8 000 000 |
| вероятность угадать 7 цифр | 10 000 000 = 107 |
| вероятность рождения пятерни (округл.)[71] | 40 000 000 |
| вероятность угадать 8 цифр | 100 000 000 = 108 |
| вероятность выиграть джекпот в лотерее "Русское лото" на 30 ходу (округл.)[78] | 150 000 000 |
| вероятность угадать 9 цифр | 1 000 000 000 = 109 |
| вероятность рождения шестерни[71] | 3 300 000 000 |
| вероятность выиграть джекпот в лотерее "Русское лото" на 25 ходу (округл.)[78] | 7 000 000 000 |
| вероятность угадать 10 цифр | 10 000 000 000 = 1010 |
| вероятность конкретному сперматозоиду мужчины достигнуть яйцеклетки женщины[79] | 220 000 000 000 |
| вероятность получить "роял-флеш" в пятикарточном покере сразу двум игрокам (округл.) | 420 000 000 000 |
| вероятность сдать на 100% тест из 20 вопросов с 4 вариантами ответов, отвечая наугад (округл.) | 1 100 000 000 000 |
| вероятность выиграть джекпот в лотерее "Русское лото" на 20 ходу (округл.)[78] | 1 500 000 000 000 |
| вероятность подобрать пароль из 10 символов содержащий только латинские буквы и цифры (округл.) | 3 600 000 000 000 000 |
| вероятность выиграть джекпот в лотерее "Русское лото" на 15 ходу (округл.)[78] | 23 000 000 000 000 000 |
| вероятность естественного распада атома Урана-238 в течение 1 секунды (округл.) [80] | 50 000 000 000 000 000 |
| вероятность получить "роял-флеш" в пятикарточном покере сразу трем игрокам (округл.) | 270 000 000 000 000 000 |
| вероятность встречи конкретного сперматозоида и конкретной яйцеклетки, для появления конкретного человека[81] | |
| вероятность получить "роял-флеш" в пятикарточном покере сразу пяти игрокам (округл.) | 1029 |
| вероятность выпадения орла 100 раз подряд при бросках монетки (округл.) | 1030 |
| вероятность того что подброшенная монетка встанет на ребро 10 раз подряд[73] | 1037 |
| вероятность квантовой телепортации атома водорода на 50 км[82] | 1045 |
| вероятность получить конкретную последовательность карт в 52-карточной колоде | 1068 |
| вероятность угадать 100 цифр | 10100 = 10102 (гугол) |
| вероятность двум парам начинающих шахматистов сыграть одинаковые партии в шахматы[83] | 10123 |
| вероятность выпадения орла 1000 раз подряд при бросках монетки (округл.) | 10301 |
| вероятность того что подброшенная монетка встанет на ребро 100 раз подряд[73] | 10377 |
| вероятность того что подброшенная монетка встанет на ребро 1000 раз подряд[73] | 103 778 |
| вероятность выигрывать джекпот в лотерее "Русское лото" на 30 ходу каждую неделю в течении 50 лет (округл.)[78] | 1021 000 |
| вероятность, согласно теории струн, родиться во вселенной (инфляционном домене) с такими законами физики как в нашей вселенной[65] | 10272 000 |
| вероятность напечатать пьесу "Гамлет" (с учетом пунктуации и заглавных букв), нажимая случайные клавиши на клавиатуре (округл.) | 10360 000 |
| вероятность что завтра на всей планете родятся только двойни[71] | 10760 000 |
| вероятность встречи конкретных сперматозоидов и яйцеклеток у всех предков до начала рода Homo, для появления конкретного человека[81] | 102 685 000 |
| вероятность рождения только мальчиков на всей планете в течении следующего года[84] | 1042 000 000 |
| вероятность квантовой телепортации вируса гриппа на 50 км[82] | 1045 000 000 |
| вероятность всем выпускникам всех школ на планете сдать на 100% тест из 20 вопросов с 4 вариантами ответов отвечая наугад (округл.) | 10400 000 000 |
| вероятность правильно подобрать пароль из 10 символов содержащий только латинские буквы и цифры ко всем электронным адресам на планете (допустим их 1 миллиард) (округл.) | 1020 000 000 000 |
| вероятность всем людям на планете выиграть джекпот в лотерее "Русское лото" на 30 ходу (округл.)[78] | 1063 000 000 000 |
| вероятность всем людям на планете, разбившись на пары, сыграть одинаковую партию в шахматы (округл.)[83] | 10470 000 000 000 |
| вероятность получить одинаковую последовательность карт, если перемешать все колоды карт на планете (допустим их 1 миллиард) (округл.) | 10680 000 000 000 |
| вероятность естественного распада 1 килограмма Урана-238 в течение 1 секунды | 101026 |
| вероятность квантовой телепортации человека на 50 км[82] | 101029 |
| вероятность квантовой телепортации человека на другой край наблюдаемой вселенной[82] | 101031 |
| вероятность естественного распада всего Урана-238 в земной коре в течение 1 секунды[85] | 101043 |
| вероятность квантовой телепортации всей нашей планеты на край наблюдаемой вселенной[82] | 101052 |
| вероятность спонтанного моментального возникновения Больцмановского мозга (мыслящего объекта массой 1кг) в результате случайных квантовых флуктуаций[69] | 101069 |
| вероятность естественного распада всего Урана-238 во всей наблюдаемой вселенной в течение 1 секунды[86] | 101071 |
| вероятность спонтанного моментального возникновения нашей планеты в результате случайных квантовых флуктуаций[69] | 101093 |
| вероятность угадать гугол цифр | 1010100 = 1010102 (гуголплекс) |
| вероятность спонтанного моментального возникновения всей наблюдаемой вселенной в результате случайных квантовых флуктуаций[69] | 1010123 |
| вероятность родиться в одном из всех возможных видов вселенных (инфляционных доменов)[67] | 1010107 |
| вероятность спонтанного моментального возникновения всей нашей вселенной (инфляционного домена с текущим "наружным" диаметром 101012 метров) в результате случайных квантовых флуктуаций[69] | 10101012 |
| вероятность спонтанного моментального возвращения всей вселенной (инфляционного домена с текущим "наружным" диаметром 101012 метров) в состояние начала большого взрыва в результате случайных квантовых флуктуаций[87] | 10101056 |
| вероятность угадать гуголплекс цифр | 101010100 = 101010102 (гуголплексплекс) |
Последнее число, которое я привожу в таблице, 101010100 - называют гуголплексплекс, в его десятичной записи после единицы должно идти гуголплекс нулей, оно больше чем любая вероятность каких-либо физических явлений, и вообще больше чем все физическое, что можно померить конечными числами в бесконечной мультивселенной (если она вообще существует, не стоит забывать, что предположение о существовании мультивселенной, хоть и разрешает многие проблемы в физике, но все же остается недоказанной гипотезой, пусть даже ее сегодня и придерживается большинство космологов). Так или иначе, с этого момента можно оставить попытки измерить большими числами что-то физическое и полностью предаться математическим забавам, забыв про сравнения с реальным миром. И я думаю многим уже не терпится начать это делать, поскольку они сообразили как создавать эти "...плексы".
10100 = гугол
1010100 = гуголплекс
101010100 = гуголплексплекс
10101010100 = гуголплексплексплекс
и т.д. каждое число невообразимо больше предыдущего
По этим безумно большим числам видно, что им очень тесно в подобной записи. Можно конечно и дальше городить башни из степеней, но если необходимо кардинально продвинуться дальше, то необходимо использовать высшие арифметические действия. Но для начала я должен объяснить, что же это такое, потому что в школе их обычно не проходят. Хотя я уверен, что многие задавались вопросом: вот есть у нас сложение, за ним умножение, потом степень, а дальше? Есть ли другие более сильные арифметические действия?
Есть, но их не проходят ни в школах, ни в институтах, даже многие люди закончившие математические факультеты ничего о них не знают, потому что эти арифметические действия не нужны, то есть совсем не нужны, и нигде не используются на практике. Однако создаются они очень просто, по принципу обычных арифметических действий. Рассмотрим как создать следующее по уровню после степени арифметические действие, называемое тетрацией:
Видите ничего сложного, по сути тетрация - это обобщение степенной башни[88], когда число возводится в степень равную ему несколько раз, к примеру так:
Ниже дана Таблица №8, в которой приведены значения тетрации для показателей 2, 3, 4 и 5. Как можно заметить, это арифметическое действие с легкостью может создать большие числа. Значения выделенные синим цветом больше чем гугол, выделенные зеленым цветом больше чем гуголплекс, выделенные красным цветом больше чем гуголплекплекс. Именно поэтому, как я и говорил, тетрация нигде не используется на практике. Вы не увидите это действие ни в одной формуле, ни в физике, ни в геометрии, ни в алгебре, ну почти нигде. Просто она создает числа бо́льшие чем нужны нам в физическом мире (кроме того тетрация не является элементарной функцией, то есть работает только с натуральными числами; показатель тетрации не может быть отрицательным, дробным или иррациональным числом, а ее обратные действия становятся невычислимыми, если не решаются в натуральных числах, поэтому тетрация бесполезна для математического анализа).
| n | 2n | 3n | 4n | 5n |
| 2 | 4 | 16 | 65536 | ≈1019728 |
| 3 | 27 | 7625597484987 | ≈101012 | ≈10101012 |
| 4 | 256 | ≈10154 | ≈1010154 | ≈101010154 |
| 5 | 3125 | ≈102184 | ≈10102184 | ≈1010102184 |
| 6 | 46656 | ≈1036305 | ≈101036305 | ≈10101036305 |
| 7 | 823543 | ≈10692974 | ≈1010692974 | ≈101010692974 |
| 8 | 16777216 | ≈1015151335 | ≈101015151335 | ≈10101015151335 |
| 9 | 387420489 | ≈10369693099 | ≈1010369693099 | ≈101010369693099 |
| 10 | 10000000000 | 1010000000000 | 101010000000000 | 10101010000000000 |
Представляю вам число, созданное американским математиком Джонатаном Бауэрсом (с другими достижениями этого человека мы еще познакомимся в дальнейшем), на основе тетрации:
А есть ли что-нибудь за тетрацией? Конечно есть. Новые арифметические действия можно вводить сколько угодно. Обобщением тетрации, например, будет пентация, это когда ...aaa b-раз, ну то есть вместо того чтобы рисовать тетрационную башню, мы просто запишем число ее ступеней (так же как ранее делали со степенной башней, обобщив ее тетрацией)[88]. Названия высшим арифметическим действиям принято давать по схеме: греческое числительное + "...ация", а для записи используют Стрелочную нотацию Кнута (известный американский программист и математик, создавший ее)[90]. Общепринятая нотация высших арифметических действий выглядит так:
и т.д.
Как можно заметить степень в такой нотации записывается через одну стрелку, а не как верхний правый показатель. Тетрация в этой нотации тоже вместо левого верхнего показателя записывается через две стрелки, и т.д. Но так легко можно запутаться в количестве этих стрелок. Я предлагаю использовать альтернативную запись высших арифметических действий, которую называют гиперопертатором[88], в ней тоже нет ничего сложного, просто вместо увеличения количества стрелок мы используем нумерацию создаваемого арифметического действия. Сложение - 1, умножение - 2, степень - 3, тетрация - 4, и т.д. Уровень арифметического действия как раз и называют гипероператором. Так вот вместо знака сложения, знака умножения или n-ного количества стрелочек мы просто будем в квадратных скобках записывать уровень арифметического действия.
и т.д.
Для всех высших арифметических действий так же как и для степени, так же как и для тетрации, не работает правило перестановок и вычислять их надо с конца, это делает число получаемое в результате вычисления во истину непостижимым. Уже результат вычисления пентации, то есть гиперопертора 5 уровня, тяжело выразить, используя даже степенную башню. Например, число 3[5]3 будет выглядеть как степенная башня из троек высотой в 7625597484987 ступеней.
Рассчитывается это очень легко
Немного передохните и идем дальше, на очереди следующий уровень арифметического действия, гексация. Число 3[6]3 уже вообще никак нельзя представить в виде степенной башни. Его можно расписать как
Понятно, что гипероператор можно увеличивать и дальше, образуя все более и более непостижимые числа. Но опять же, по сути, мы топчемся на месте. Следующий шаг требует нехило напрячь воображение. Обычно объяснение масштаба числа, которое я сейчас представлю, всегда используют, как вводный экскурс в теорию больших чисел, не буду делать исключение и я. Итак представляю Число Грема - многими популярными изданиями оно позиционировалось как самое большое число, которое когда-либо использовалось в математике для доказательств[91]. Конечно же это не так, в математике для доказательств используются и намного бо́льшие числа, более того, как вы в дальнейшем поймете, существование некоторых сверхбольших чисел само по себе важный аргумент в теории доказательств.
Но перед тем как постигать масштаб Числа Грэма, я попробую в двух словах объяснить смысл этого числа. Число Грэма на самом деле ничего не доказывает, это была просто верхняя оценка в первой попытке найти решение одной из задачи по теории Рамсея. В дальнейшем мы еще рассмотрим теорию Рамсея подробнее, в двух словах, это некоторая смесь из комбинаторики и теории графов[92]. Суть задачи можно объяснить следующим образом. У нас есть куб, все вершины которого соединены прямыми линиями: вертикальными, горизонтальными, диагональными. Мы вольны раскрасить все эти линии в любой из двух цветов: красный или синий. Наша задача состоит в том, чтобы сделать это так, чтобы отрезки находящиеся в одной плоскости были разного цвета. Иными слова чтобы не возникла такая фигура:
Для обычного куба эту задачу очень просто решить, причем разным числом способов. Мы можем раскрасить линии внутри нашего куба хотя бы так:
Но что если наш куб будет иметь не три, а четыре измерения. Да, представить такой куб невозможно, но в математике такие объекты существуют (подробнее о них смотрите в Приложении №2). Можно ли тогда решить эту задачу? Ответ: можно. И если будет пять измерений, то задача тоже решается. Однако Теорема Рамсея утверждает, что рано или поздно, увеличивая число измерений куба, мы уже не сможем решить эту задачу, и как бы мы не раскрашивали линии куба, у нас все равно где-нибудь да получится плоскость раскрашенная в один цвет. Вопрос стоит так: сколько измерений должно быть у куба, чтобы правило раскраски обязательно бы нарушались. Ответ неизвестен до сих пор, но первая поытка решить эту задачу дала верхнюю границу равную Числу Грэма (то есть минимальное число измерений точно не должно превышать Число Грэма)[92]. Стоит сказать, что на сегодняшний день (начало 2020), математики серьезно продвинулись в решении задачи[93][94] и верхнюю границу довольно сильно понизили, и теперь мы знаем что минимальное число измерений должно лежать в диапозоне: 13 < N < 51322. Иными словами ответ должен быть даже меньше чем 3[6]3, так что сегодня Число Грэма вообще не имеет никакой практической значимости, кроме показательного примера очень большого числа.
Двухмерный куб он же квадрат мы можем легко изобразить:
Не обращайте внимание на то что он повернут, так что стоит на своем углу, это называется ортогональная проекция. С двухмерными объектами все просто, у них есть два измерения длина и ширина и изображаем мы их тоже на двухмерной поверхности. У квадрата имеется четыре стороны. Давайте отметим каждую по отдельности:
Теперь изобразим трехмерный объект, собственно обычный куб, в ортогональной проекции:
Некоторым вероятно будет сложно увидеть в этой фигуре куб, потому что это не сам куб а его проекция на двухмерную плоскость. Но ведь и своим зрением вы видим плоские объекты и наш мозг достраивает их трехмерность мысленно. Поэтому в отличие от квадарта не возможно увидеть сразу все строны куба. Если вы все еще не увидили в этой фигуре куб, то давайте я вам помогу, заштриховав пунктиром те грани, которые не должны видеть у реального плотного куба:
Стороны трехмерного куба являются двухмерными квадратами, всего у него их шесть и называются они гранями. Давайте так же отметим каждую по отдельности:

А еще у куба 12 ребер, которые являются у него обычными отрезками, и как вы понимаете увидеть все их одновременно у реальной плотной фигуры тоже не получится. Однако в сущности мы способны видеть еще в одном измерении, во времени, и если мы заставим куб вращаться, то увидим все его грани и ребра, буквально прочувовав трехмерность этой фигуры, но на самом деле мы по-прежнему видим всего лишь сменяющиеся проекции.

Кроме того, благодаря времени, мы можем увидеть как склеить куб из его сторон изначально лежащих в одной плоскости, но я думаю и в этом примере вы прекрасно осознаете, что это всего лишь последовательность кадров, а трехмерность создается нашим пространственным мышлением.
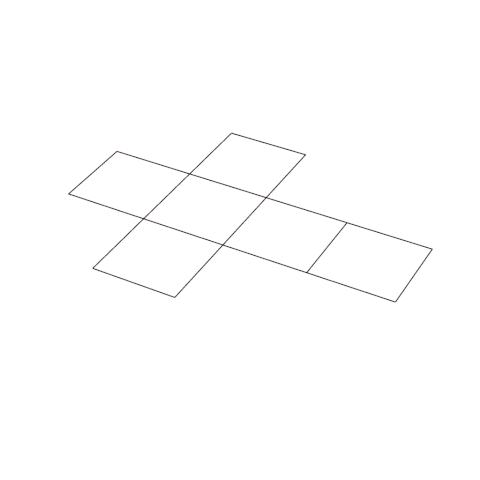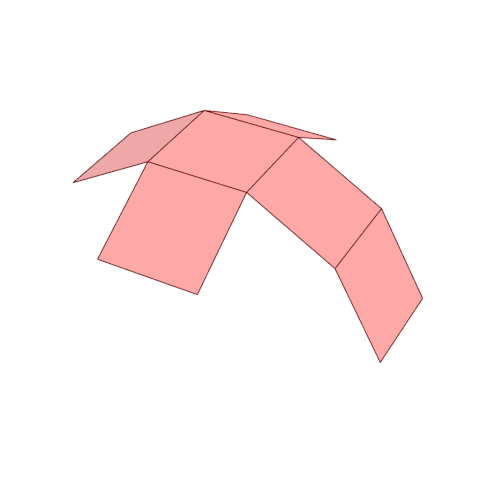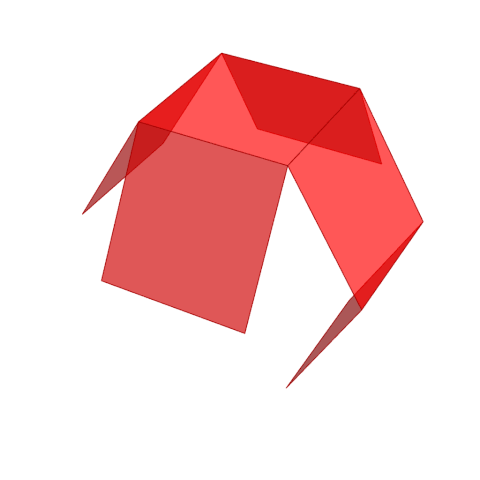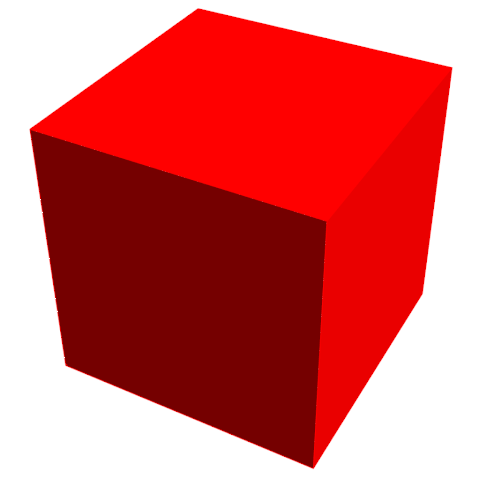
И вот теперь вы готовы взглянуть на ортогональную проекцию четырехмерного куба.
Иначе эту фигуру называют тессеракт. Мы в принципе неспособны представить его в истинной четырехмерной форме, поскольку наше пространственное мышление развилось и существует в трехмерном пространстве. У тессеракта так же есть стороны для него это трехмерные кубы, всего он обладает восемью сторонами. А вот их по-отдельности найти в этой ортогональную проекции будет несложно:
Гранями для тессеракта являются уже квадраты всего у него их 24, попробуйте отыскать их все самостоятельно. Так же мы можем, подключив время и заставив тессеракт вращаться, увидеть как меняются проекции этой фигуры на двухмерную плоскость, но это не поможет нам увидеть его четырехмерность.

Можно посмотреть, опять конечно же в двухмерной проекции, как тессеракт разворачивается на свои трехмерные стороны, а потом снова собирается из них, осознания четырехмерности это не прибавит.
Еще как вариант можно посмотреть на то как создаются измерения. Легко понять как из точки возникает отрезок, а из отрезка строится квадарат, но при переходе к построению куба уже задействуется пространственное мышление, однако когда аналогичным медотом из куба создается тессеракт пространственное мышление нас подводит, и нам по-прежнему кажется что перед нами трехмерная фигура.

И так мы можем увеличивать число измерений, создавая все более многомерные фигуры, но наше восприятие не сможет увидеть эту многомерность. Вот, к примеру пентеракт, вернее его ортогональная проекция на двухмерную плоскость.
У пентеракта десять сторон, каждая из которых является тессерактом, но вы вряд ли сможете найти их в этой фигуре, зато сможете отыскать 40 граней, которые для пентеракта уже являются кубами. Ну и можно посмотреть на двухмерную проекцию вращающегося пентеракта.

С каждым дополнительным измерением фигуры становятся все более сложными, так же как и их ортогональные проекции. Ниже приведены ортогональные проекции шестимерного куба (гексеракт), восьмимерного куба (октеракт) и десятимерного куба (декеракт).

Теперь давайте вернемся к масштабу Числа Грэма, той самой первой оценки для решения этой задачи. Итак, для построения этого числа нам нужно сам гипероператор, то есть уровень арифметического действия увеличить до размера 3[6]3. Здесь, внимание: то есть, это будет ни тетрация, ни пентация, а 3[6]3-ация. Тогда мы должны записать новое полученное число вот так 3[3[6]3]3. А если и это число мы используем как гиперопертор, тогда получим 3[3[3[6]3]3]3. Короче так вкладывать гипероператоры можно бесконечно и уровень невообразимости числа будет невообразимо возрастать. Итак, представляю вам число Грэма:
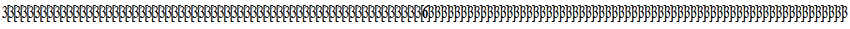
Всего 64 вложения гипероператоров[91]. Вот такая рекурсия. Поскольку это слово будет постоянно использоваться дальше, напомню для всех самый наглядный ответ на вопрос, что оно означает:

Масштаб Числа Грема для тех, кто о нем ничего не слышал, кажется непостижимым, а многие кто уже знают о масштабе этого числа, считают что это своего рода предел для больших чисел в математике. Но это скорее только начало. Просто дальше начинают сравнивать уже не масштаб числа, а масштаб рекурсии, что его создает, поскольку осознание самого истинного сравнительного масштаба числа уже недоступно человеческой психике. Нас с вами тоже ничто не останавливает перед созданием рекурсии, которая создаст еще бо́льшее числа. Начнем с простенькой рекурсии, которую можно представить визуально.
Сразу предлагаю исключить такие банальности как Число Грэма умноженное на Число Грэма, или Число Грэма в степени Числа Грэма, или даже Число Грэма с гипероператором Числа Грэма. И так видно, что Число Грэма чувствует себя в гипероперационной нотации еще более скованно, чем Гугол в десятичной нотации. Поэтому, чтобы совершить новый скачек нам нужны другие более сильные нотации. Можно ли придумать такие нотации? Конечно можно, и их напридумано великое множество. Но они очень сильные, и вот так сразу без подготовки посвящать вас в них мне бы не хотелось, потому что большинство из них слишком абстрактные и их практически невозможно показать наглядно. Поэтому я предлагаю свою нотацию с наглядной визуальной рекурсией, которую я назвал расширенным гипероператором.
Я думаю не только одному мне пришло в голову, что можно не рисовать все эти вложения гипероператоров в числе Грэма, а как-то их записать. Предлагаю сделать это вот так: 3[6,64]3 - что значит,
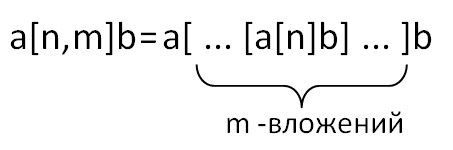
Но на самом деле я предлагаю пойти еще дальше, мы можем ввести в нотацию еще одно число, которое будет считать не только вложения, но и вложения вложений:
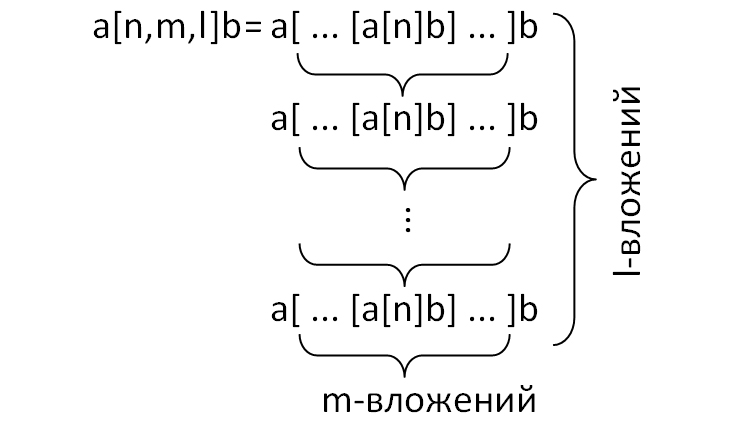
И если
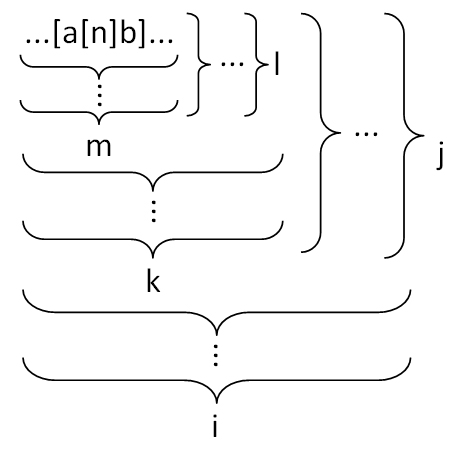
И так далее, в общем, я думаю, принцип понятен. С каждым дополнительно подставляемым внутрь гипероператора числом уровень рекурсий растет, как собственно и уровень невообразимости числа, которое они создают. Получается, что обязательным числом, которое подставляется внутрь гипероператора, является только первое, все остальные по умолчанию равны "1".
Но мы на этом не остановимся, предлагаю обобщить всю эту схему двумя квадратными скобками. Это и будет называться расширенным гипероператором. Раскрываться двойные скобки будут по следующей формуле:
3[[1]]3 это всего лишь
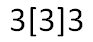
А вот
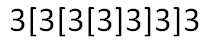
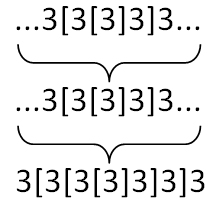
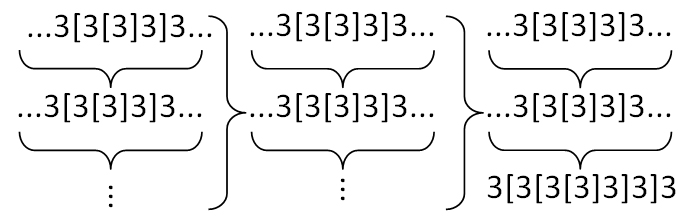
Дальше расширяем нотацию по прежней схеме, добавляя внутрь двойной скобки еще числа, через запятую, каждое из которых будет показывать соответствующий уровень вложений, но уже для двух скобок:
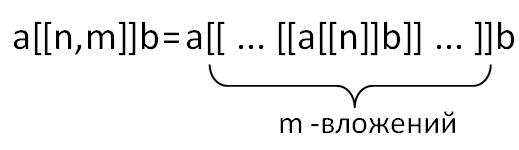
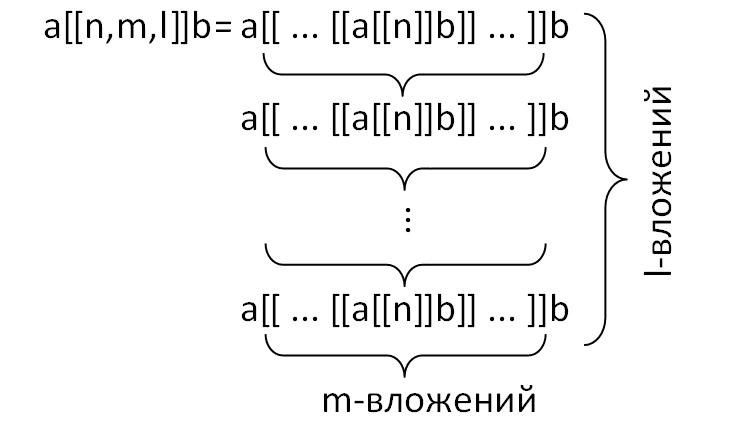
Следовательно можно привести аналогичные примеры только для двух скобок с добавлением одного числа:
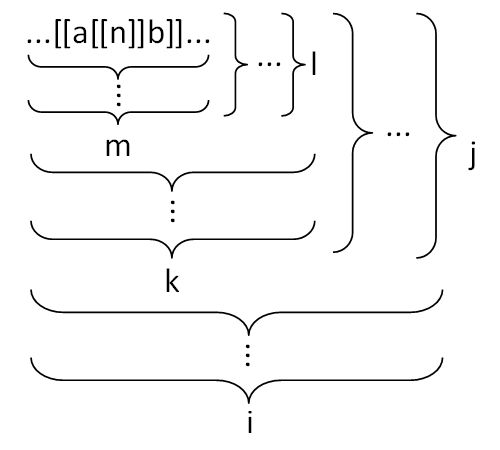
Затем снова можно обобщить все это уже тремя скобками, чтоб все работало вот так:
На этом я и приглашаю вас во вторую часть книги, где мы разберем что такое бесконечность, и есть ли что-либо бо́льшее чем она. Конечно, вы можете спросить: не рановато ли для бесконечности, а как же сверхсильные нотации и самое большое из придуманных чисел, оно явно меньше бесконечности, почему бы в начале не поговорить о нем. Однако поверьте, чтобы понять масштаб сверхсильных нотаций, и тем более масштаб самого большого из придуманных чисел нужно вначале понять, что такое бесконечность, и есть ли что-нибудь за ее пределами. Как бы странно это не звучало, но постижение масштаба больших чисел, идет параллельно с изучением бесконечности.