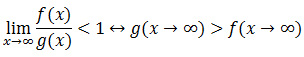Часть III Рекурсии на бесконечных рекурсиях
Не может существовать нечто, что можно было бы назвать самым большим, всегда можно создать что-то, что будет еще больше, а значит можно создать то, что будет даже больше бесконечности - одно из следствий Аксиомы бесконечности
В этой части мы возвращаемся к основной теме, к созданию больших чисел. Для начала вспомним все, что мы уже знаем о больших числах. Во-первых, любое по-настоящему большое число является формализацией, то есть некой условной записью. Представить это число в его естественном количественном виде непосильная задача для человеческого мозга. Во-вторых, мы знаем, что существуют нотации для создания чисел, то есть это некие условные записи цифр и знаков, которые дают нам возможность выразить числа. С математической точки зрения нотации представляют собой функции, в которые мы подставляем меньшие числа (цифры), чтобы получить бо́льшие числа. Чем больше в результате получается число, тем сильнее считается нотация. Но что лежит в основе силы нотаций, то есть функций, которыми они по сути являются? Ответ: чаще всего это рекурсии (есть и другие методы, которые даже еще сильнее, но мы их рассмотрим в дальнейшем). Так или иначе, при создании самого большого числа, все сводится к созданию самой быстрорастущей функции. То есть основным критерием таких функций будет следующее правило: подставляя меньшие аргументы (значения, которые функция принимает) мы получаем все бо́льшие результаты. В этой и следующих нескольких частях мы рассмотрим именно рекурсивные функции, вероятно это будет самой обширной темой моего повествования.
Перед тем как продолжить давайте дадим более общее определение понятию функция в математике, нежели чем то что вы проходили в школе. В теории множеств функцией называют зависимость между множествами, когда каждому элементу одного множества ставится в соответствие некоторый элемент из другого множества. Например, функция f[сопоставление по составу] на множестве A{медная гайка, медный гвоздь, железная гайка, железный гвоздь} по множеству B{железо, медь}, записывается так f(a) = b, где a - элемент множества A, b - сопоставляемый ему элемент из множества B. При этом, a - называют аргументом функции, b - называют значением функции, множество A - называют областью определения функции, множество B - называют областью значений функции. Вот один из примеров работы функции: f(медная гайка) = медь.
Вроде бы все очевидно, и порой даже кажется, что теория множеств лишь усложняет интуитивные вещи. Но ее прелесть в том, что методы теории множеств одинаково применимы как к простым так и к сложным вещам. Вообще разновидностей функций великое множество, но нам нужен именно определенный вид - быстрорастущие функции. Для создания такого вида функций нужно сопоставить множеству натуральных чисел, такое множество, чтобы меньшие числа множества натуральных сопоставлялись с как можно бо́льшими числами из этого множества. Вот сравните три функции: счет чисел: f(n) = n+1, удвоение числа: f(n) = 2×n и квадрат числа: f(n) = n2. В первом случае каждому из элементов множества натуральных чисел {0,1,2,3,4,...} сопоставляются элементы {1,2,3,4,5,...}, во втором случае сопоставляются элементы {0,2,4,6,8,...}, а в третьем случае элементы {0,1,4,9,16,...}. Очевидно, что третья функция растет быстрее всех, вторая чуть медленнее, и самым медленным ростом из этих трех функций обладает первая. Но заметьте что разгоняются они по разному, и глядя на первые сопоставления, можно сделать совсем иной вывод. Поэтому важно скорость роста функций определять не по первым элементам, а перспективно, или как говорят математики, по мере того как аргумент стремится к бесконечности. Формально сравнение скорости роста функций определяется так:
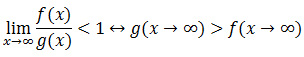
Аргументов у функции может быть несколько, разница будет лишь в том, что сопоставляться у нас будут не два множества, а больше. Например, функция f(n,m) = 2×n+m сопоставляет два множества натуральных чисел M и N, с результирующим множеством. Но для нас это не особо важно, мы всегда можем в определении функции сделать так: m = n и упростить ее: f(n) = 2×n+n, что так же ее усилит, и более того, как вы поймете в дальнейшем, это станет ключевым правилом для создания рекурсий.
Нотация - это тоже функция, а цифры являются ее аргументами. И как я объяснял в первой части, даже десятичная нотация является функцией, просто мы к ней привыкли, но мы можем выразить ее результат иначе, допустим, в натуральном виде, палочками. Например, число "12" в десятичной нотации - это два аргумента (в данном случае это базовые цифры 1 и 2), которые подставлены в функцию десятичного позиционного счисления: 12 = ||||||||||||, или число "κα" в древнегреческой нотации - это два аргумента, которые подставлены в функцию десятичного непозиционного счисления: κα = |||||||||||||||||||||.
Кроме того хотелось бы, чтобы запись числа выглядела лаконично. Не как гугол в десятичной нотации (Рисунок №1) и не как число Грема в гипероперационной нотации (Рисунок №15). Так что сила функции или нотации будет определяться не только скоростью роста, но и краткостью записи. Поэтому давайте мы с вами определим границы для записи числа, которое позволяет сделать нотация или функция. Договоримся о следующем: запись не должна превышать по содержанию 20 символов. Тогда максимальное число в десятичной нотации будет равно 99999999999999999999 (девяносто девять секстиллионов девятьсот девяносто девять квинтиллионов девятьсот девяносто девять квадриллионов девятьсот девяносто девять триллионов девятьсот девяносто девять миллиардов девятьсот девяносто девять миллионов девятьсот девяносто девять тысяч девятьсот девяносто девять). Для выражения логарифмической нотации возьмем не запись вида 10n, а метод программистов (это позволит использовать дополнительный символ), но и в этом случае логарифмическая нотация закончится на E9999999999999999999, что больше чем гугол, но даже близко не дотягивает до гуголплекса. После логарифмической записи сразу рассмотрим гипероперационную, которая позволяет создавать вообще уже невообразимые числа, но записать число Грэма в 20 символах и ей не по зубам. Для этого мы можем воспользоваться расширенным гипероператором - нотацией, которую я создал в первой части, и записать Число Грэма так: 3[6,64]3. В общем, я думаю, основной принцип понятен.
Ну и как я говорил в первой части, рекурсии большинства быстрорастущих функций и нотаций, которые мы будем с вами рассматривать, становятся настолько сильными, что их невозможно визуализировать и чтобы осознавать масштабы создаваемых чисел нам нужен другой инструмент, который так же должен выступать в качестве универсального стандарта для сравнения силы этих нотаций и функций. Хорошо что такой измерительный эталон существует. В математике есть семейство функций, которые называют Функциями быстрорастущей иерархии, по-английски: Fast-growing hierarchy (FGH)[140]. Вот их обычно и используют, чтобы сопоставлять с другими быстрорастущими функциями и измерять скорость, с которой они растут. Поэтому если мы хотим добраться до самых больших придуманных чисел, нам нужно понять что же это за функции быстрорастущей иерархии. Для начало дам формальное определение:
f0(n) = n+1.
fα+1(n) = fαn(n) = fα(fα(fα(...fα(n)...))) - n вложений.
fα(n) = fα[n](n), где α - предельный ординал,
α[n] - n-ный элемент фундаментальной последовательности ординала α.
Скорее всего многие ничего из этого определения не поняли, поэтому давайте разбираться наглядно, на примерах. Первая в семействе функций быстрорастущей иерархии это f0(n), по сути, как следует из определения, это просто итерация n+1, или проще говоря, обычный счет:
f0(1) = 1+1 = 2
f0(2) = 2+1 = 3
f0(3) = 3+1 = 4
f0(4) = 4+1 = 5
Ничего сложного, это очень медленно растущая функция, но не самая медленная, которую только можно задать на натуральных числах. Например, можно придумать такую функцию: счет нечетных чисел, которая будет расти еще медленнее, результирующее множество будет выглядеть так {0,1,1,2,2,...}. Ноль - четное число - значит функция вернет ноль. Единица - нечетное число - функция вернет один. Двойка - четная, но до нее уже была нечетная единица - значит функция по-прежнему вернет один. Три - нечетное число, уже второе по счету - значит функция вернет два. И так далее. Можно придумать еще более медленно растущую функцию: счет чисел кратных трем. Потом, счет чисел кратных четырем. Ну и далее, в том же духе, короче говоря, самой медленно растущей функции не существует так же как и самой быстрорастущей. Более того, зачастую, они напрямую зависят друг от друга, определив некую быстрорастущую функцию всегда можно определить и обратную ей медленно растущую, и наоборот. Необходимо понимать, что пределов в гугологии нет. Покуда существует аксиома бесконечности не может быть ничего самого самого: ни множества всех множеств, ни самого большого ординала или кардинала, ни самого большого натурального числа, ни самой быстро или медленно растущей функции. Но все же это не значит, что мы не должны попытаться проверить способности нашего разума в постижении того, что скрывает эта бесконечность, и какие числа могут встретиться на вечном пути к ней.
Но вместо того чтобы грезить о недостижимом финише вернемся к нашей отправной точке, к функции счета. Конечно это очень медленный способ достижения больших чисел. Функция банального сложения (n+m) растет и то быстрее, потому как мы можем подставить любое число m, а не только 1. Теперь внимание! Функция дублирования: n+n, считается еще более быстрорастущей, чем сложение. Это очень важно понимать! В случае сложения (n+m) мы зависим от двух аргументов и чтобы увеличить результат нам нужно увеличить оба слагаемых, в случае дублирования же участвует всего один аргумент: n+n = 2×n, а значит для увеличения результата требуется меньше изменений внутри функции. Сформулируем это правило: среди двух почти одинаково растущих функций более быстрорастущей считается та, которая использует меньше аргументов. Это называют принципом диагонализации, а почему этот принцип имеет такое название я поясню на примере таблицы сложения, которую проходят в первом классе. В левом верхнем углу таблицы находятся самые малые ее значения, а в правом нижнем углу самые большие. Кратчайший путь от самых малых до самых больших значений будет пролегать по диагонали, как раз по тому пути и проходит функция дублирования: n+n.

рис.53 (таблица сложения)
Теперь давайте измерим эти функции нашим измерительным эталоном - функциями быстрорастущей иерархии. Следующей в этом семействе будет функция f1(n), она определяется рекурсивно от предыдущей функции f0(n). Объясняю что это значит: чтобы вычислить f1(n) нужно сначала вычислить f0(n), причем не просто вычислить а подставить саму в себя n-ное количество раз. Вот как это выглядит:
f1(1) = f0(1) = 1+1 = 2
f1(2) = f0(f0(2)) = (2+1)+1 = 4
f1(3) = f0(f0(f0(3))) = ((3+1)+1)+1 = 6
f1(4) = f0(f0(f0(f0(4)))) = (((4+1)+1)+1)+1 = 8
и т.д.
f1(n) = f0(f0(f0(...(n)...))) - n вложений
Когда функцию нужно рекурсивно вложить саму в себя несколько раз, это обычно записывают так fn( ). То есть, мы можем более кратко записать: f1(n) = f0n(n). Так же выходит, что f1(n) эквивалентна дублированию, то есть f1(n) = 2×n, значит это одинаково быстрорастущие функции.
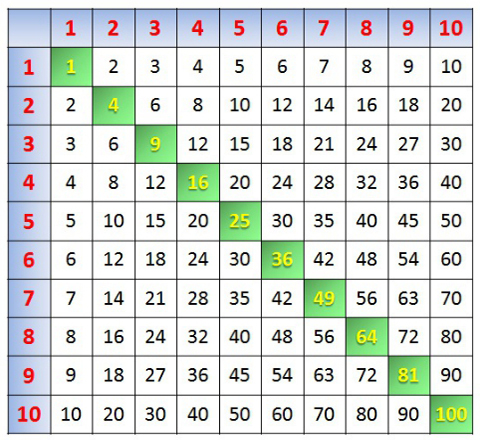
Идем дальше. Умножение (n×m) растет еще быстрее, поскольку мы вольны умножать не только на 2, а на любое число m. Возведение в квадрат имеет еще более быстрый рост, это происходит по той же причине, из-за которой дублирование растет быстрее сложения, банально, функции требуется всего один аргумент вместо двух: n2 = n×n. Принцип диагонализации снова в действии, достаточно взглянуть на всем нам знакомую таблицу умножения, чтобы увидеть, что квадраты чисел расположены в ней по диагонали, и это кратчайший путь от малых значений к большим.
рис.54 (таблица умножения)
Возведение в куб (n3 = n×n×n) будет расти еще быстрее, возведение в четвертую степень (n4 = n×n×n×n) еще быстрее, и так далее... С увеличением показателя степени (nm = n×n×n×... - m-раз) скорость роста функции будет увеличиваться.
Интересно то, что знакомый нам со второй части булеан 2n, растет быстрее любой степенной функции. Потому что это уже не степенная, а показательная функция. Дело в том, что nm отличается от mn, потому что во-первых степень некоммутативная операция, то есть от перестановки основания с показателем результат изменится, и бо́льший вклад в рост этой функции дает именно показатель. Ну а во-вторых, важно понимать, что из принципа диагонализации следует, что аргумент n - основной, а аргумент m - дополнительный (еще иногда в математике основной аргумент называют свободной переменной, а дополнительный - параметром). Значит мы должны считать функции более быстрорастущими, если увеличение именно основного аргумента приводит к бо́льшим результатам. Этот принцип наглядно можно продемонстрировать на следующих примерах:
52 = 25 < 25 = 32
103 = 1000 < 210 = 1024
174 = 83521 < 217 = 131072
235 = 6436343 < 223 = 8388608
306 = 729000000 < 230 = 1073741824
377 = 94931877133 < 237 = 137438953472
и т.д.
Из этих примеров следует, что для того чтобы соответствовать заданной скорости роста в функции nm аргумент m тоже должен расти, при том что в функции mn аргумент m может оставаться неизменным, и это доказывает, что показательные функции растут быстрее степенных.
Здесь снова переходим к функциям быстрорастущей иерархии. Следующая на очереди f2(n), которая определяется так же рекурсивно f2(n) = f1n(n).
f2(n) = f1(f1(f1(...(n)...))) - n вложений, где каждый f1(n) = f0(f0(f0(...(n)...))) - n вложений.
Иными словами мы уже имеем рекурсию внутри рекурсии. Вот так это рассчитывается:
f2(1) = f1(1) = f0(1) = 1+1 = 2
f2(2) = f1(f1(2)) = f1(4) = 8
f2(3) = f1(f1(f1(3))) = f1(f1(6)) = f1(12) = 24
f2(4) = f1(f1(f1(f1(4)))) = f1(f1(f1(8))) = f1(f1(16)) = f1(32) = 64
Следовательно, f2(n) растет быстрее, чем булеан и равна: 2n×n.
А вот перед тем как разбирать уровень роста f3(n), мы можем рассмотреть еще несколько других функций, которые растут намного медленнее нее и в то же время очень быстро для наших привычных масштабов. Например, функция 10n, которая лежит в основе логарифмической нотации, та самая при помощи которой обычно кратко записывают астрономически большие числа, типа размера вселенной, количества атомов в ней, или все тот же пресловутый гугол: 10100. Эта функция растет быстрее чем f2(n), так же как и любая другая показательная функция mn, при условии, что ее основание m > 2. Однако нотация и функция, которая лежит в ее основе, это немного не одно и тоже. Для нотации важны правила записи аргументов. Например, десятичная и логарифмическая нотации принимают в качестве аргументов не все числа, а только те, которые выражены цифрами. И если другие функции тоже ограничить, разрешив подставлять в качестве аргументов лишь однозначные числа, то мы можем сравнить скорость роста чисел, которые можно записывать нотациями. Для десятичной нотации, например, скорость роста можно определить так:
9×9 < 99 < 9×9×9
9×9×9 < 999 < 9×9×9×9
9n < (n-значная десятичная нотация состоящая из цифр 9) < 9n+1
Логарифмическая нотация растет быстрее
99 < E9 < 99×9
99×9 < E99 < 99×9×9
99n < (n-значная логарифмическая нотация состоящая из цифр 9) < 99n+1
Если мы введем функцию maxdec(n), которая будет определять максимальное число, которое можно написать в десятичной нотации с использованием n цифр, то получим соответствие maxdec(n) = 10n-1 и получается, что даже в таком виде мы имеем скорость роста меньше, чем у показательной функции с произвольным основанием mn (однако аналогичная функция для логарифмической нотации maxlog(n) = 1010n-1 будет намного быстрее, и этот уровень роста мы еще рассмотрим в дальнейшем).
Функция nn, назовем ее самостепень, растет еще быстрее, чем любая показательная функция mn, причину этого я уже объяснял дважды и повторятся не буду, это все тот же принцип диагонализации. Где-то между ними затесался факториал (mn < n! < nn), любимая функция комбинаторики, та самая, которая считает число возможных перестановок в системе: n! = 1×2×3×...×n. Скорость роста этой функции уже поражает воображение, так например, число перестановок в обычной колоде карт соизмеримо с астрономическими величинами. Интересно то, что факториал стартует медленнее логарифмической нотации, но уже на E25 < 25! ≈ 1,55×1025 обгоняет ее. Факториал (n!) всегда обгонит показательную функцию mn какое бы основание степени мы не взяли (обгон точно произойдет на значении n, большем чем m×e, где e ≈ 2,7182818284... - Число Эйлера). Однако при этом факториал никогда не догонит самостепень. Это наглядный пример того, как принцип диагонализации делает функции еще более быстрорастущими, и что между функцией c двумя и более аргументами и ее диагонализацией по уровню скорости роста может вклиниться еще какая-нибудь функция.
24 = 16 < 4! = 24 < 44 = 256
37 = 2187 < 7! = 5040 < 77 = 823543
49 = 262144 < 9! = 362880 < 99 = 387420489
512 = 244140625 < 12! = 479001600 < 1212 = 8916100448256
и т.д.
Вот вам еще несколько таких примеров. Аналог факториала, только для сложения называется функцией треугольного числа: T(n) = 1+2+3+4+...+n. Данная функция растет быстрее функции умножения на произвольное число (n×m), всякий раз обгоняя ее на значении n, большем чем m×2, однако ее рост медленнее чем у функции квадрата (n×n). Можно даже вывести строгое соответствие между ростом этих функций n2 = T(n)+T(n-1).
(3×2) = 6 = T(3) = 6 < 32 = 9
(4×2) = 8 < T(4) = 10 < 42 = 16
(5×3) = 15 = T(5) = 15 < 52 = 25
(6×3) = 18 < T(6) = 21< 62 = 36
(7×4) = 28 = T(7) = 28 < 72 = 49
(8×4) = 32 < T(8) = 36 < 82 = 64
(9×5) = 45 = T(9) = 45 < 92 = 81
(10×5) = 50 < T(10) = 55 < 102 = 100
(11×6) = 66 = T(11) = 66 < 112 = 121
и т.д.
Другая знаменитая функция, которая носит имя итальянского математика Фибоначчи, тоже вклинивается по скорости роста, но уже между степенными (nm) и показательными функциями (mn). Функция Фиббоначи - это одна из первых известных человечеству рекурсивно-определенных функций: следующее значение функции есть сумма двух предыдущих, или более формально F(n) = {F(n > 1) = F(n-1)+F(n-2); F(1) = 1; F(0) = 0}[141]. Функция создает следующую последовательность чисел {0,1,1,2,3,5,8,13,21,34,55,89,144,...} и имеет глубокий смысл, она выводится из принципов золотого сечения, а ее проявления можно повсюду отследить в природе. Что касается ее скорости роста, то Функция Фиббоначи F(n) всегда обгонит степенную функцию (nm) (это точно произойдет на значении n, большем m×logФ(n), где Ф ≈ 1,6180339887... - Золотое сечение). Однако уже булеан (2n) обходит Функцию Фиббоначи F(n) сразу и по всем значениям n.
142 = 196 < F(14) = 233 < 214 = 16384
223 = 10648 < F(22) = 10946 < 222 = 4194304
324 = 1048576 < F(32) = 1346269 < 232 = 4294967296
425 = 130691232 < F(42) = 165580141 < 242 = 4398046511104
и т.д.
А вот вам еще две вклинивающиеся функции суперфакториал: n$ = 1!×2!×3!×...×n!, и гиперфакториал: n$ = 11×22×33×...×nn, которые растут намного быстрее чем обычный факториал, быстрее чем самостепень (nn) и даже быстрее функции nn×m, но все же медленнее чем nn2. Cуперфакториал[142] и гиперфакториал[143] редко используют на практике, но нам для наглядности изучения скорости роста функций они подходят, причем как следует из названия гиперфакториал растет быстрее, чем суперфакториал. Интересно, что скорость роста обоих функций сложно точно определить по отдельности, однако она легко определяется при их совместном использовании: n$×n$ = n!n+1.
44×1 = 256 < 4$ = 288 < 442 = 4294967296
88×2 ≈ 2,8×1014 < 8$ ≈ 5×1015 < 882 ≈ 6,2×1057
1111×3 ≈ 2,3×1034 < 11$ ≈ 2,65×1035 < 11112 ≈ 10126
1414×4 ≈ 1,5×1064 < 14$ ≈ 6,9×1064 < 14142 ≈ 4,4×10224
и т.д.
33×1 = 27 < 3$ = 108 < 332 = 19683
55×2 = 9765625 < 5$ = 86400000 < 552≈ 3×1017
77×3 ≈ 5,6×1017 < 7$ ≈ 3,3×1018 < 772≈ 2,5×1041
1010×4 = 1040 < 10$ ≈ 2,15×1044 < 10102 = 10100
и т.д.
Степенная башня даже из трех этажей обгоняет и эти функции. Здесь мы уже найдем введеную нами ранее функцию maxlog(n), которая определяет максимальное число, которое можно написать в логарифмической нотации с использованием n цифр, и соотвествует 1010n-1, что быстрее чем nn2, nn10 и 22n. Чтобы впредь не путаться в соотвествиях, думаю стоит расставить варианты трехэтажной степенной башни в порядке скорости их роста в зависимости от наличия и положения постоянного аргумента внутри башни: nnm < mmn < nmn < mnn < nnn (где, напомню, m - играет роль постоянного аргумента функции).
И даже между этими вариантами степенной башни можно вклинить функции, занимающие промежуточное место по скорости роста. Например, то что можно назвать мультипликативной функцией Фиббоначи: MF(n) = {MF(n > 1) = MF(n-1)×MF(n-2); MF(1) = 2; MF(0) = 1}, когда следующее значение функции есть произведение двух предыдущих. Только чтобы функция корректно работала, в ее определении первых два члена надо заменить с {0,1} на {1,2} и тогда мы получим последовательность {1,2,2,4,8,32,256,8192,2097152,...} общая скорость роста которой оценивается так nnm < MF(n) < 22n. Существует интересная закономерность связывающая эту функцию с обычной функцией Фиббоначи: MF(n) = 2F(n).
11111 ≈ 2,85×1011 < MF(11) ≈ 3,6×1016 < 2211 ≈ 3,2×10616
18182 ≈ 5,1×10406 < MF(18) ≈ 5,55×10480 < 2218 ≈ 1,6×1078913
27273 ≈ 3,4×1028173 < MF(27) ≈ 8,6×1036542 < 2227 ≈ 1,2×1040403562
и т.д.
Так же для примера еще одной вклинившейся функции мы можем определить функцию вложенного треугольного числа Tn(n), которая считается рекурсивно: T1(1) = T(1), T2(2) = T(T(2)), T3(3) = T(T(T(3))), и т.д., скорость ее роста будет лежать в пределах между m2n < Tn(n) < n2n.
224 = 65536 < T4(4) = 1186570 < 424= 4294967296
326 ≈ 3,4×1030 < T6(6) ≈ 2×1033 < 626 ≈ 6,3×1049
428 ≈ 1,3×10154 < T8(8) ≈ 5,7×10161 < 828 ≈ 1,5×10231
и т.д.
Ну а чем больше у степенной башни будет этажей, тем больше будет скорость роста, к тому же, как вы могли заметить, при наличии постоянных аргументов в башне бо́льший вклад в рост функции дает положение именно основного аргумента n, чем выше он находится в башне, тем функция растет быстрее. В конечном счете мы можем выразить произвольную степенную башню как тетрацию mn. Как я отмечал в первой части, скорость роста этой функции огромна, и уже 34 ≈ 10154 будет больше, чем гугол. Аналогично как и в степени, если мы сделаем основным аргументом не основание, а показатель тетрации nm, то увеличим ее скорость роста, назовем такую функцию показательно-тетрационной. Кроме того мы можем определить то, что можно назвать самотетрацией nn и в соответствии с принципом диагонализации она будет расти еще быстрее.
И так же между функциями mn, nm и nn по скорости роста можно вставить другие функции. Например, то что можно назвать степенной функцией Фиббоначи: ↑F(n) = {↑F(n > 1) = ↑F(n-1)↑F(n-2); ↑F(n) = 2; ↑F(n) = 1}, когда следующее значение функции определяется как возведение текущего значения в степень равную предыдущему значению. Последовательность будет выглядеть так {1,2,2,4,16,65536,6553616,...}. Данную функцию можно усилить, поменяв показатель и основание в определении функции, и для корректной работы изменив первые два члена с {1,2} на {2,2}. Получившуюся функцию можно будет назвать показательно-степенной функцией Фиббоначи: F↑(n) = {F↑(n) = (F↑(n-2)F↑(n-1); F↑(1) = 2; F↑(0) = 2}, когда следующее значение функции определяется как возведение предыдущего значения в степень равную текущему значению. В итоге ее последовательность будет такой: {2,2,4,16,4294967296,164294967296,...}. Или еще для одного примера возьмем то, что называют степенным факториалом n! = n...321, который будет расти еще быстрее[144], чем обе представленные выше функции. Скорость роста всех трех функций можно определить так: mn < ↑F(n) < F↑(n) < n! < n2. А еще мы можем определить функцию, которая будет расти быстрее показательно-тетрационной, но медленнее самотетрации, назовем ее вложенный факториал n!n, который считается рекурсивно: 1!1 = 1! , 2!2 = (2!)! , 3!3 = ((3)!)!)! , 4!4 = (((4)!)!)!)! и т.д., скорость ее роста будет лежать в пределах между nm < n!n < nn.
Где-то здесь, за пределами этих функций, по уровню скорости роста и располагается f3(n). К сожалению, не существует точного соответствия f3(n) с тетрацией или с другими арифметическими действиями, поэтому мы уже не можем одной формулой выразить правило ее вычисления. Мы знаем, только, что она точно растет быстрее самотретации: nn < f3(n). Но думаю, если вы вспомните предыдущие функции быстрорастущей иерархии, то принцип вычисления и этой функции вам станет понятен, поэтому сразу привожу примеры:
f3(1) = f2(1) = f1(1) = f0(1) = 1+1 = 2
f3(2) = f2(f2(2)) = f2(8) = 2048
f3(3) = f2(f2(f2(3))) = f2(f2(24)) = f2(402653184) = 2402653184×402653184 ≈ 10109
f3(4) = f2(f2(f2(f2(4)))) = f2(f2(f2(64))) = f2(f2(264×64)) = f2(2(264×64)×264×64) = 22(264×64)×264×64×2(264×64)×264×64 ≈ 10101021
Отсюда при выражении высших арифметических действий я предлагаю сразу прибегать к гипероперационной записи. Можно точно сказать, что самотетрация nn = n[4]n растет медленне чем f3(n), но функция n+1n = n[4](n+1) растет уже быстрее чем f3(n). Значит и любая пентация n[5]m, где m>2, тоже растет быстрее чем f3(n). Потом можно разместить тетрационную функцию Фиббоначи ↑↑F(n) = ↑F[4](n), за ней показательно-тетрационную функцию Фиббоначи F↑↑(n) = F↑[4](n), следом тетрационный факториал: !n = n[4]! = n[4]...3[4]2[4]1 = 123...n, затем идет показательно-пентационная функция m[5]n. Дальше, аналогично предыдущему уровню, идет вложенный степенной факториал n!n = n[3]!n, а за ним самопентация n[5]n. И только потом располагается f4(n), так что: n[5]n < f4(n) < n[5](n+1). И давайте я в последний раз приведу примеры с правилами вычисления функции быстрорастущей иерархии:
f4(1) = f3(1) = f2(1) = f1(1) = f0(1) = 1+1 = 2
f4(2) = f3(f3(2)) = f2(2048) ≈ 10[4](1011)
f4(3) = f3(f3(f3(3))) ≈ 10[4]10[4](10109)
f4(4) = f3(f3(f3(f3(4)))) ≈ 10[4]10[4]10[4](10101021)
И так далее по тому же принципу, увеличивая уровень арифметического действия, можно пройтись по всему гипероператору, располагая функции по скорости роста. Мы даже можем вывести общие принципы сопоставления функций:
n[1]1 = f0(n) < n[1]2 < n[1]m < n[2]2
n[2]2 = f1(n) < n[2]m < n[1]! < n[3]2 < n[3]m < F[1](n) < 2[3]n
2[3]n < f2(n) < m[3]n < n[2]! < n[3]n < (n[2]!)[3]2 < (n[2]!)[3]m
(n[2]!)[3]m < n[3](n[2]m) < n$ < n$ < n[3]n[3]m < F[2](n) = 2[3]F[1](n) < 2[3]2[3]n < m[3]2[3]n
m[3]2[3]n < n[1]!n < n[3]2[3]n < n[3]m[3]n < m[3]n[3]n < n[4]3 ≤ n[4]m
n[4]m < ↑F[3](n) < F↑[3](n) < n[3]! < 2[4]n < m[4]n < n[2]!n < n[4]n < f3(n) < n[4](n+1) < n[5]m
n[5]m < ↑F[4](n) < F↑[4](n) < n[4]! < 2[5]n < m[5]n < n[3]!n < n[5]n < f4(n) < n[5](n+1) < n[k]m
n[k]m < ↑F[k-1](n) < F↑[k-1](n) < n[k-1]! < 2[k]n < m[k]n < n[k-2]!n < n[k]n < fk-1(n) < n[k](n+1) < fk(n)
Примечание: во всех выражениях m > 2 и k > 5;
n$ - суперфакториал, n$ - гиперфакториал;
n[1]! - треугольное число, n[2]! - факториал;
n[3]! - степенной факториал, n[4]! - тетрационный факториал и т.д;
n[1]!n - вложенное треугольное число, n[2]!n - вложенный факториал и т.д;
F[1](n) - функция Фиббоначи, F[2](n) - мультипликативная функция Фиббоначи;
↑F[3](n) - степенная функция Фиббоначи, F↑[3](n) - показательно-степенная функция Фиббоначи и т.д.
↑F[4](n) - тетрационная функция Фиббоначи, F↑[4](n) - показательно-тетрационная функция Фиббоначи и т.д.
Можем так же выразить все что здесь записали, без использования гипероператора, выражая высшие арифметические действия в более привычной для математиков Стрелочной нотации Кнута:
n+1 = f0(n) < n+2 < n+m < n×2
n×2 = f1(n) < n×m < T(n) < n↑2 < n↑m < F(n) < 2↑n
2↑n < f2(n) < m↑n < n! < n↑n < (n!)↑2 < (n!)↑m
(n!)↑m < n↑(n×m) < n$ < n$ < n↑n↑m < MF(n) = 2F(n) < 2↑2↑n < m↑2↑n
m↑2↑n < Tn(n) < n↑2↑n < n↑m↑n < m↑n↑n < n↑↑3 ≤ n↑↑m
n↑↑m < ↑F(n) < F↑(n) < n↑! < 2↑↑n < m↑↑n < n!n < n↑↑n < f3(n) < n↑↑(n+1) < n↑↑↑m
n↑↑↑m < ↑↑F(n) < F↑↑(n) < n↑↑! < 2↑↑↑n < m↑↑↑n < n↑!n < n↑↑↑n < f4(n) < n↑↑↑(n+1) < n↑km
n↑km < ↑k-1F(n) < F↑k-1(n) < n↑k-1! < 2↑kn < m↑kn < n↑k-2!n < n↑kn < fk+1(n) < n↑k(n+1) < fk+2(n)
Примечание: во всех выражениях m > 2 и k > 3;
n$ - суперфакториал, n$ - гиперфакториал;
T(n) - треугольное число, n! - факториал;
n↑! - степенной факториал, n↑↑! - тетрационный факториал и т.д;
Tn(n) - вложенное треугольное число, n!n - вложенный факториал и т.д;
F(n) - функция Фиббоначи, MF(n) - мультипликативная функция Фиббоначи;
↑F(n) - степенная функция Фиббоначи, F↑(n) - показательно-степенная функция Фиббоначи;
↑↑F(n) - тетрационная функция Фиббоначи, F↑↑(n) - показательно-тетрационная функция Фиббоначи и т.д.
Казалось бы ну и в чем же прелесть функций быстрорастущей иерархии, если уже на гипероперторе (функции, рекурсии которой вполне можно наглядно продемонстрировать) они почти сравниваются с ним по скорости роста. Вот для этого нам и потребуется бесконечность, но обо всем по порядку. Для начала в функциях быстрорастущей иерархии перейдем на новый уровень рекурсий. Как мы уже уяснили n[k]n растет быстрее чем n[k]m или m[k]n при любом гипероператоре, начиная со сложения, умножения и так далее, потому что согласно принципу диагонализации для роста функции нужно меньше аргументов. Этот же принцип можно применить и к функциям быстрорастущей иерархии: fn(n) будет расти быстрее, чем fk(n). Но так же она будет расти и быстрее, чем гипероператор типа n[k]m, или типа n[k]n и даже быстрее, чем n[n]n. Она растет даже быстрее Стрелочной нотации Кнута, которая отличается от гипероператора лишь: n↑km = n[k+2]m, но все же n[n]n < n↑nn. В итоге мы получили очень быстрорастущую функцию:
n[k]m < m[k]n < n[k]n < n[n]n < ↑F[n](n) < F↑[n](n) < n[n]! < n[n]!n < n↑nn < fn(n)
Перед тем как идти дальше, давайте рассмотрим как создаются быстрорастущие функции. Зачастую большие рекурсии задаются не одной функцией, и в состав сложной рекурсивной функции входят другие функции попроще. В программировании рекурсивные функции принято делить на примитивные и частично-определенные. Примитивно-рекурсивным функциям можно дать простое определение, это такие функции, которые можно переписать на языке программирования с использованием циклов, в которых число итераций известно на момент начала цикла, то есть на момент написания программы можно точно определить, что в ней не возникнет бесконечной петли и она не зависнет. Если разложить примитивно-рекурсивную функцию на составляющие, то они должны быть трех видов: функция нуля O(x) = 0, которая всегда обнуляет результат в независимости от аргумента; функция следования S(x) = x+1, которая увеличивает аргумент на единицу; функция проекции U(n,i,x1,x2,x3,...xi,...,xn) = xi, где 1 ≤ i ≤ n, которая выбирает один из своих аргументов[145]. Если рекурсивную функцию нельзя разложить на эти составляющие, то такая рекурсия не является примитивной и относится к частично-определенным, то есть в процессе ее вычисления могут возникать исключения, неопределенные значения или бесконечные циклы. Одна из первых открытых и самых простых частично-определенных функций, которая при этом вычисляется для любых аргументов, называется Функцией Аккермана[146]. Этой функцией сегодня тестируют вычислительные способности компиляторов программного кода. Определяется функция следующим образом:
A(m,n) = n+1, если m = 0;
A(m,n) = A(m-1,1), если m > 0 и n = 0;
A(m,n) = A(m-1,A(m,n-1)), если m > 0 и n > 0.
Такую функцию нельзя переписать на языке программирования с использованием циклов, в которых число итераций известно на момент начала цикла. Однако эта функция вычисляется для любого аргумента, который мы в нее подставим и кроме того растет очень и очень быстро. Результат вычисления Функции Аккермана можно выразить на языке гипероператора A(m,n) = (2[m](n+3))-3, и это значит растет она быстрее чем n[n]n и даже n↑nn, но все же медленнее чем fn(n). Кроме того возможность выразить Функцию Аккермана через гипероператор доказывает, что функции k[n]m и соответственно k↑nm, в которых n - свободная переменная, не являются примитивно-рекурсивными (для программистов: это значит, что их нельзя написать без использования цикла "while", который нельзя выразить как цикл "for").
Числа, которые создаются этими функциями очень большие, но они вполне могут быть описаны в рамках аксиом Пеано (аксиом арифметики первого порядка), которые мы с вами рассмотрели в предыдущей части. Однако иногда аксиоматику арифметики раскладывают на подсистемы для того, чтобы было удобнее изучать арифметические построения. Одна из таких подсистем называется Примитивно-рекурсивной арифметикой (PRA), аксиомы такой подсистемы применимы только к примитивно-рекурсивным функциям, и математическая индукция ограничена только в пределах этих функций[147]. То есть в соответствии с теоремой Геделя о Неполноте невозможно создать такую примитивную рекурсию (без использования циклов while), которая могла бы создать числа сопоставимые с числами создаваемыми fn(n). То есть в PRA можно создать функцию гипероператора любого уровня, но не самогипероператор n[n]n. Кроме того, основываясь на аксиомах этой подсистемы, невозможно создать такую неоднородность в бесконечности, которая бы превысила уровень ωω, то есть множество алгебраических чисел еще возможно, но вычисление интегралов уже лежит за пределами этой подсистемы аксиом. Получается, что ωω это теоретико-доказательственный ординал или Proof-Theoretic Ordinal (далее буду писать просто "PTO") для Примитивно-рекурсивной арифметики, а что это такое мы выяснили еще во второй части, это максимальный ординал упорядочивающий множество, которое доказуемо способна создать теория (там же мы выяснили, что этот ординал всегда будет лежать за пределами теории). Стоит отметить, что множество алгебраических чисел мы "расселили" в отель с помощью формулы факториазции простых чисел, в которой не использовалась даже тетрация, не говоря уже о бо́льших гипероператорах, что могут быть построены в рамках PRA. Однако, как вы должны помнить, если расселять не всевозможные решения степенных уравнений, а только решения уравнений с определенной степенью, то метод факторизации простых чисел становится избыточен, потому что создает бо́льшую разряженность при расселении, нежели симплексное распределение, которое расселяет вплотную, следовательно факторизация простых чисел является более быстрорастущей функцией. Так вот PRA допускает и более разряженное расселение, ведь в данном случае, когда мы говорим о макcимально-возможной рекурсии, которую можно создать в рамках теории, то это должно соотноситься с максимально возможными методами расселения в наш "натуральный отель" счетных множеств, которые только может выделить теория.
Другая еще более простая подсистема называется Элементарно-функциональной арифметикой (EFA), это такая подсистема, акиомы которой определены только для сложения, умножения и степени, а математическая индукция, соответственно, ограничена только в пределах этих действий[148]. Такая подсистема будет еще слабее, и максимально-возможная рекурсия, которую можно создать на основе аксиом этой подсистемы будет слабее f3(n), то есть уже тетрация лежит за пределами возможностей этой теории. А максимальная неоднородность, которую можно создать в бесконечности, будет равна ω3, это и будет PTO теории, то есть, например, множество решений квадратных уравнений EFA описать еще способна, но вот множество решений кубических уравнений уже нет, то есть создание полноценной алгебры уже невозможно в рамках этой теории. Хотя опять же методы "расселения" множества решений квадратных уравнений в наш "натуральный отель" могут быть разные, вплоть до использования степенных башен.
Подсистему арифметики можно упростить еще сильнее, взять к примеру, Рудиментарно-функциональную арифметику (RFA), это такая подсистема, аксиомы которой определены только для сложения и умножения, а математическая индукция ограничена только в пределах этих действий[149]. Уже в основе f2(n) лежит такая рекурсия, которая в принципе не может быть создана на основе аксиом RFA, то есть даже функция булеана, неопределяемая в рамках данной теории. При этом максимальная неоднородность, которую можно создать в бесконечности (то есть PTO теории) будет равна ω2. Получается что RFA способна описать лишь множество рациональных чисел и на ней возможно описание только линейной алгебры.
Но пожалуй самой простой подсистемой является Арифметика Робинсона (обозначают как Q, не путайте с обозначением рациональных чисел), в этой подсистеме определены аксиомы сложения и умножения, но не существует аксиомы индукции[150], поэтому невозможно определить понятие диагонализации, а значит функции квадрата и дублирования не могут быть корректно определены. Отсюда можно сделать вывод, что это самая слабая подсистема и уже рекурсия уровня f1(n) будет лежать за пределами ее возможностей. На основе аксиом Арифметики Робинсона невозможно доказать даже теорему о коммунитативности слагаемых (a+b = b+a), можно лишь показать справедливость этого правила для частных случаев, а это в свою очередь не позволит создать отрицательные числа, а значит в рамках теории мы навсегда останемся только в натуральных числах и создать какую-либо неоднородность в бесконечности вовсе не получится (полноценная алгебра в Q вообще невозможна), поэтому PTO теории будет лишь ω.
Получается, что в соответствии с Теоремой Геделя о Неполноте, для любой аксиоматической системы, которая включает или выводит натуральные числа (тем самым включая или подразумевая бесконечность), существует максимально возможная рекурсия для создания больших чисел и максимально возможный ординал для упорядочивания бесконечности. Значит у нас есть, как минимум, два способа для измерения силы аксиоматических систем (на самом деле их три, но о третьем я расскажу намного позже, когда мы разберемся с рекурсиями).
Расширенный гипероператор - нотация, которую я продемонстрировал вам в первой части, и на которой лаконично можно выразить Число Грэма, растет быстрее чем fn(n) и любые примитивные рекурсии. Чтобы померить ее скорость роста функциями быстрорастущей иерархии нам и понадобятся трансфинитные ординалы. Функцию fn(n) принято обозначать как fω(n). Это всего лишь хитрый трюк. Из второй части мы помним, что ω - это первый трансфинитный ординал, обозначающий упорядоченность в бесконечности. Но в функциях быстрорастущей иерархии значек ω не связан с бесконечностью, он используется чтобы создавать диагонализационные рекурсии. Когда мы разбирали трансфинитные ординалы, вы должны были убедиться, что каждый ординал, который на порядок больше предыдущего, построен на новой рекурсии. Всякий раз когда мы создавали неоднородность в бесконечности, пытаясь заселить в отель все более сложную систему из бесконечных постояльцев, в сущности мы просто создавали рекурсии. Вот и математики решили, зачем изобретать велосипед, и позаимствовали эти рекурсии для функций быстрорастущей иерархии.
Теперь следите за тем, как создаются рекурсии на основе трансфинитных ординалов: fω+1(n) = fω(fω(fω(...(n)...))) - n вложений, или как мы уже знаем, более корректно это можно записать так fω+1(n) = fωn(n).
Это очень сильный скачек вперед. То есть в выражении fω(fω(n)) мы изначально вычисляем fω(n) = fn(n), а затем, внимание, fω(fn(n)) = ffn(n)(fn(n)). А выражение fω(fω(fω(n))) уже расписывается таким образом: fω(fω(fω(n))) = fω(fω(fn(n))) = fω(ffn(n)(fn(n))) = fffn(n)(fn(n))(ffn(n)(fn(n))). В итоге получаем, что общая схема рекурсии такова: fω+1(n) = fff...fn(n)...(...)(...)(...) - n раз. Поэтому fω+1(n) растет намного быстрее, чем скажем fn[n]n(n). И уже такое число: fω+1(64) будет намного больше, чем Число Грэма.
Соответственно, дальше идет: fω+2(n) = fω+1n(n) = fω+1(fω+1(fω+1(...(n)...))) - n вложений, за ним следует fω+3(n) = fω+2n(n) = fω+2(fω+2(fω+2(...(n)...))) - n вложений, и так далее. И уже где-то здесь по скорости роста расположился первый уровень расширенного гипероператора:
fω(n) > n[n]n
fω+1(n) > n[n,n]n = n[n[n[...n...]n]n]n n вложений
fω+2(n) > n[n,n,n]n = n[n,n[n,n[n,...n...]n]n]n n вложений
fω+3(n) > n[n,n,n,n]n = n[n,n,n[n,n,n[n,n,...n...]n]n]n n вложений
fω+k(n) > n[n,n,n,n,...k+1 раз...]n
Переход на следующий уровень рекурсии выглядит так: fω+n(n) = fω+ω(n) = fω×2(n). Дальше опять происходит резкий скачек, выражение fω+ω(fω+ω(n)) будет вычисляться так fω+fω+n(n)(fω+n(n)), еще бо́льшая вложенность fω+ω(fω+ω(fω+ω(n))) будет вычисляться так fω+fω+fω+n(n)(fω+n(n))(fω+fω+n(n)(fω+n(n))), тогда получается, что общая схема рекурсии будет такой: fω×2+1(n) = fω+fω+fω+...fω+n(n)...(...)(...)(...) - n раз.
Ну а дальше по тому же принципу: fω×2+2(n) = fω×2+1n(n) = fω×2+1(fω×2+1(fω×2+1(...(n)...))) - n вложений, затем fω×2+3(n) = fω×2+2n(n) = fω×2+2(fω×2+2(fω×2+2(...(n)...))) - n вложений, и так далее. Таковой будет скорость роста второго уровня расширенного гипероператора:
fω×2(n) > n[[n]]n = n[n,n,n,n,...n раз...]n
fω×2+1(n) > n[[n,n]]n = n[[n[[n[[...n...]]n]]n]]n n вложений
fω×2+2(n) > n[[n,n,n]]n = n[[n,n[[n,n[[n,...n...]]n]]n]]n n вложений
fω×2+3(n) > n[[n,n,n,n]]n = n[[n,n,n[[n,n,n[[n,n,...n...]]n]]n]]n n вложений
fω×2+k(n) > n[[n,n,n,n,...k+1 раз...]]n
Аналогичным образом можно создать функции быстрорастущей иерархии, которые будут сопоставимы с третьим уровнем расширенного гипероператора: fω×2+n(n) = fω×2+ω(n) = fω×3(n). Ну и дальше, по общей схеме: fω×3+1(n) = fω×2+fω×2+fω×2+...fω×2+n(n)...(...)(...)(...) - n раз.
А потом снова fω×3+2(n) = fω×3+1n(n) = fω×3+1(fω×3+1(fω×3+1(...(n)...))) - n вложений, затем таким же образом: fω×3+3(n) = fω×3+2n(n) = fω×3+2(fω×3+2(fω×3+2(...(n)...))) - n вложений, и так далее. Так будет расти уже трижды расширенный гипероператор:
fω×3(n) > n[[[n]]]n = n[[n,n,n,n,...n раз...]]n
fω×3+1(n) > n[[[n,n]]]n = n[[[n[[[n[[[...n...]]]n]]]n]]]n n вложений
fω×3+2(n) > n[[[n,n,n]]]n = n[[[n,n[[[n,n[[[n,...n...]]]n]]]n]]]n n вложений
fω×3+3(n) > n[[[n,n,n,n]]]n = n[[[n,n,n[[[n,n,n[[[n,n,...n...]]]n]]]n]]]n n вложений
fω×3+k(n) > n[[[n,n,n,n,...k+1 раз...]]]n
Плагаю, что общая схема уже давно всем стала понятна: fω×m+n(n) = fω×m+ω(n) = fω×(m+1)(n). После чего следует скачек: fω×(m+1)+1(n) = fω×m+fω×m+fω×m+...fω×m+n(n)...(...)(...)(...) - n раз. А потом каждый раз рекурсируем так: fω×m+k+1(n) = fω×m+kn(n) = fω×m+k(fω×m+k(fω×m+k(...(n)...))) - n вложений.
Так можно продолжать и дальше до уровня fω×n(n) = fω×ω(n) = fω2(n). Многие уже вероятно уловили принцип построения рекурсий на основе трансфинитных ординалов, так например: fω×ω(fω×ω(n)) = fω×fω×n(n)(fω×n(n)), а еще бо́льшая вложенность: fω×ω(fω×ω(fω×ω(n))) = fω×fω×fω×n(n)(fω×n(n))(fω×fω×n(n)(fω×n(n))). В итоге мы имеем новый рекурсивный скачек: fω2+1(n) = fω×fω×fω×...fω×n(n)...(...)(...)(...) - n раз. Но мы перешли предел еще до этого скачка, так как уже функция fω2(n) будет расти быстрее, чем расширенный гипероператор.
fω(n) > n[n]1n = n[n]n
fω×2(n) > n[n]2n = n[[n]]n
fω×3(n) > n[n]3n = n[[[n]]]n
fω×4(n) > n[n]4n = n[[[[n]]]]n
fω×5(n) > n[n]5n = n[[[[[n]]]]]n
fω×ω(n) > n[n]nn = n[[[[[...n...]]]]]n n вложений
Пусть созданные нами визуальные рекурсии из первой части уже не справятся с fω2(n), но как я и говорил существуют другие нотации для записи больших чисел, рекурсии которых уже сложно визуализировать. Однако есть определенные математические правила, по которым их нужно вычислять. Я без лишних упрощений или пояснений буду приводить правила вычисления этих нотаций в приложениях, потому что алгоритм их вычисления является залогом того, что создаваемое нотацией большое число реально и точно вычисляется. Поэтому правила должны быть записаны в строгом формальном виде, как инструкции для компьютерной программы. Пусть не расстраиваются те, кто не желает разбираться в этих правилах, или кто ничего из них не поймет, я буду разъяснять как они работают на примерах. К тому же у нас теперь есть возможность сравнить эти нотации с функциями быстрорастущей иерархии и понять скорость их роста, даже не вникая в процесс их вычисления. Если внимательно следить за этими сравнениями, то можно будет и легко проследить за силой этих нотаций и сравнить нотации между собой. Я не буду приводить все существующие нотации для записи сверхбольших чисел, останавлюсь на самых широко используемых, в конце концов наша задача создать как можно бо́льшее число, а не изучать все придуманные рекурсии.
приложение 8 (Цепная нотация)
Одна из первых нотаций для записи больших чисел была придумана английским математиком Джоном Конвеем в 1995 году и называетя Цепной нотацией Конвея[5]. Она задумывалась как расширение Стрелочной нотации Кнута, и в случае если в Цепной нотации используются всего три аргумента, то она повторяет действие Стрелочной нотации.
n↑m = n↑1m = n[3]m = n→m→1 = n→m
n↑↑m = n↑2m = n[4]m = n→m→2 = n→(n→(...n...)) m-1 вложений
n↑↑↑m = n↑3m = n[5]m = n→m→3 = n→(n→(...n...)→2)→2 m-1 вложений
n↑↑↑↑m = n↑4m = n[6]m = n→m→4 = n→(n→(...n...)→3)→3 m-1 вложений
n↑km = n[k+2]m = n→m→k
Начиная с добавления четвертого аргумента Цепная нотация начинает быстро расти, и становится уже сопоставима с расширенным гипероператором:
fω(n) > n[n+2]n = n→n→n→1 = n→n→n
fω+1(n) > n[3,n]n = n→n→n→2 = n→n→(n→n→(...n→n...)) n-1 вложений
fω+2(n) > n[3,nn,n]n = n→n→n→3 = n→n→(n→n→(...n→n...)→2)→2 n-1 вложений
fω+3(n) > n[3,nn,nn,n]n = n→n→n→4 = n→n→(n→n→(...n→n...)→3)→3 n-1 вложений
Рекурсии, в которые преобразуется цепная нотация, легко проследить на приведенных выше примерах. Они будут создаваться аналогично для каждого следующего аргумента. Так уже пятый аргумент цепной нотации приблизительно сопоставим с дважды расширенным гипероператором:
fω×2(n) > n[[n]]n ≈ n→n→n→n→1 = n→n→n→n
fω×2+1(n) > n[[n,n]]n ≈ n→n→n→n→2 = n→n→n→(n→n→n→(...n→n→n...)) n-1 вложений
fω×2+2(n) > n[[n,n,n]]n ≈ n→n→n→n→3 = n→n→n→(n→n→n→(...n→n→n...)→2)→2 n-1 вложений
fω×2+3(n) > n[[n,n,n,n]]n ≈ n→n→n→n→4 = n→n→n→(n→n→n→(...n→n→n...)→3)→3 n-1 вложений
Ну в общем, продолжая добавлять аргументы в цепную нотацию, мы можем сопоставлять ее со все новыми уровнями расширения гипероператора.
fω(n) > n[n+2]n = n→n→n
fω×2(n) > n[[n]]n ≈ n→n→n→n
fω×3(n) > n[[[n]]]n ≈ n→n→n→n→n
fω×4(n) > n[[[[n]]]]n ≈ n→n→n→n→n→n
fω×5(n) > n[[[[[n]]]]]n ≈ n→n→n→n→n→n→n
fω×ω(n) > n[n]nn ≈ n→n→n→n→n→n→...длиной n+2
Получается что Цепная нотация Конвея растет так же быстро как и моя нотация расширенного гипероператора. Однако как наверное многие заметили, из данных соответствий: n[n+2]n = n→n→n, и n[[n]]n = n[n,n,n,...]n, где n аргуметнов в скобках, и n→n→n→n = n[3,nn,nn,...,n]n, где n аргументов в скобках, следует что n[[n]]n < n→n→n→n. Значит, начиная со второго уровня расширения гипероператора, рекурсии лежащие в обоих нотациях можно соотнести лишь приблизительно (из-за этого же, кстати, Цепная нотация Конвея не позволяет точно выразить Число Грэма, можно сказать лишь что 3→3→64→2 < Число Грэма < 3→3→65→2). Значит следует держать в уме, что, и n[[[n]]]n < n→n→n→n→n, и n[[[[n]]]]n < n→n→n→n→n→n, и т.д. Причем, то насколько цепная нотация в даннном случае будет создавать бо́льшие числа нежели расширенный гипероператор, многократно превосходит наше привычное понимание "немного больше", однако поскольку обе рекурсии все равно значительно уступают соотвествующему уровню функций быстрорастущей иерархии, я и поставил в сравнительных выражениях знак приблизительного равенства.
Но все же, мы так и не преодолели fω2(n) по скорости роста, а ведь мы можем определить еще более быстрорастущую функцию fω3(n), что эвивалентно fω2×n(n) = fω2×ω(n) = fω3(n) и соответственно fω3+1(n) = fω2×fω2×fω2×...fω2×n(n)...(...)(...)(...) - n раз, а затем определить: fω3×n(n) = fω3×ω(n) = fω4(n) и соответственно fω4+1(n) = fω3×fω3×fω3×...fω3×n(n)...(...)(...)(...) - n раз, и так далее. Однако есть способ усилить цепную нотацию, чтобы перейти оба этих предела, его придумал другой математик Питер Хёрфорд[151]. Этот способ действует аналогично тому, который применялся в Стрелочной нотации Кнута, где a↑↑b можно было записать иначе как a↑2b, и означало это тетрацию, то есть последовательное возведение в степень, начиная с конца, a↑a↑a↑a↑... и так b - раз. В свою очередь a↑↑↑b иначе записываемое как a↑3b, означало уже пентацию, определяющуюся как последовательное тетрирование, начиная с конца, a↑↑a↑↑a↑↑a↑↑... и так b - раз, и т.д. Цепная нотация Конвея тоже вычисляется с конца и так же может быть усилена подобным обобщением, только чтобы не рисовать несколько горизонтальных стрелок Хёрфорд сразу решил подписывать уровень стрелки. Согласно его способу мы можем определить a→2b как цепочку a→a→a→a→... содержащую b аргументов, или, будем говорить проще, длиной b. Тогда a→3b будет означать цепочку a→2a→2a→2a→2... длиной b, но уже соединенную стрелочками второго уровня "→2", и т.д. Давайте переформулируем правила вычисления нотации и приведем сравнительные примеры.
приложение 9 (Расширенная цепная нотация)
fω2(n) > n→2n = n→n→n→n→...длиной n
fω2+1(n) > n→2n→2 = n→2(n→2(...n...)) n-1 вложений
fω2+2(n) > n→2n→3 = n→2(n→2(...n...)→2)→2 n-1 вложений
fω2+ω(n) > n→2n→n = n→2(n→2(...n...)→n-1)→n-1 n-1 вложений
fω2+ω+1(n) > n→2n→n→2 = n→2n→(n→2n→(...n→2n...)) n-1 вложений
fω2+ω×2(n) > n→2n→n→n = n→2n→(n→2n→(...n→2n...)→n-1)→n-1 n-1 вложений
fω2+ω×2+1(n) > n→2n→n→n→2 = n→2n→n→(n→2n→n→(...n→2n→n...)) n-1 вложений
fω2+ω×3(n) > n→2n→n→n→n = n→2n→n→(n→2n→n→(...n→2n→n...)→n-1)→n-1 n-1 вложений
fω2×2(n) > n→2n→2n = n→2(n→n→n→n→...длиной n)
fω2×2+1(n) > n→2n→2n→2 = n→2n→2(n→2n→2(...n→2n...)) n-1 вложений
fω2×2+2(n) > n→2n→2n→3 = n→2n→2(n→2n→2(...n→2n...)→2)→2 n-1 вложений
fω2×2+ω(n) > n→2n→2n→n = n→2n→2(n→2n→2(...n→2n...)→n-1)→n-1 - n-1 вложений
fω2×2+ω+1(n) > n→2n→2n→n→2 = n→2n→2n→(n→2n→2n→(...n→2n→2n...)) n-1 вложений
fω2×2+ω×2(n) > n→2n→2n→n→n = n→2n→2n→(n→2n→2n→(...n→2n→2n...)→n-1)→n-1 n-1 вложений
fω2×3(n) > n→2n→2n→2n = n→2n→2(n→n→n→n→...длиной n)
fω2×4(n) > n→2n→2n→2n→2n = n→2n→2n→2(n→n→n→n→...длиной n)
fω3(n) > n→3n = n→2n→2n→2n→2...длиной n
fω3+1(n) > n→3n→2 = n→3(n→3(...n...)) n-1 вложений
fω3+ω(n) > n→3n→n = n→3(n→3(...n...)→n-1)→n-1 n-1 вложений
fω3+ω2(n) > n→3n→2n = n→3(n→n→n→n→...длиной n)
fω3×2(n) > n→3n→3n = n→3(n→2n→2n→2n→2...длиной n)
fω3×3(n) > n→3n→3n→3n = n→3n→3(n→2n→2n→2n→2...длиной n)
fω4(n) > n→4n = n→3n→3n→3n→3...длиной n
fω5(n) > n→5n = n→4n→4n→4n→4...длиной n
fωω(n) > n→nn = n→n-1n→n-1n→n-1n→n-1...длиной n
Таким образом, получается, что Расширенная цепная нотация растет почти так же быстро как fωω(n). Эта функция является продолжением функций fω3(n), fω4(n), ..., fωk(n), и означает: fωn(n) = fωω(n). Для преодоления этого предела нам опять нужен скачек в виде fωω+1(n). Чтобы показать как будет работать этот скачек, мне необходимо показать принципы вложения этой функции самой в себя, а чтобы это нагляднее выглядело запишем возведение в степень в функции через Стрелочную нотацию Кнута: fωω(n)=fω↑ω(n). Тогда одиночная вложенность будет выражаться так: fω↑ω(fω↑ω(n)) = fω↑fω↑n(n)(fω↑n(n)), а еще бо́льшая вложенность будет выражаться так: fω↑ω(fω↑ω(fω↑ω(n))) = fω↑fω↑fω↑n(n)(fω↑n(n))(fω↑fω↑n(n)(fω↑n(n))). В итоге следующая функция в семействе быстрорастущей иерархии будет выглядеть так: fωω+1(n) = fω↑fω↑fω↑...fω↑n(n)...(...)(...)(...) - n раз.
Но на этом этапе мы немного отвлечемся от нотаций, ведь и помимо них в математике есть множество других быстрорастущих функций. Например, примерно с этой же скоростью, которую мы достигли, растет Функция блочной субпоследовательности Фридмана[152]. Теорема создающая столь быстрорастущую функцию тоже происходит из области комбинаторики, как в принципе и большинство быстрорастущих функций не являющихся нотациями. Cмысл функции заключается в следующем: у нас имеется строка из последовательности символов x1, x2, x3, ... , где n это количество видов символов. Например, строку ACBA можно расписать так: x1 = A, x2 = B, x3 = C, x4 = A, n = 3 (A,B,C). "Правильной последовательностью" будем называть такую, в которой субпоследовательность xi, xi+1, ..., xi×2 не входит в другую субпоследовательность xj, xj+1, ..., xj×2, где i < j. Американский математик Харви Фридман доказал, что "правильные последовательности" всегда будут конечными из скольких бы видов символов мы бы не составляли последовательность. Функция BST(n) означает максимальную длину "правильной последовательности", которую можно составить из n видов символов. Для одного элемента BST(1) значение функции равно 3, такую наибольшую длину может иметь "правильная последовательность" составленная из одного вида символов. A - правильная, AA - правильная, AAA - правильная, но AAAA - уже неправильная, потому что субпоследовательность x1, x2 (AA) является частью субпоследовательности x2, x3, x4 (AAA). В свою очередь BST(2) = 11, и тогда самая длинная "правильная последовательность" будет выглядеть так ABBBAAAAAAB или так ABBBAAAAAAA. Давайте проверим их "правильность", в соответствии с правилами, мы можем составить из каждой из них субпоследовательности: x1, x2 (AB) ; x2, x3, x4 (BBB) ; x3, x4, x5, x6 (BBAA) ; x4, x5, x6, x7, x8 (BAAAA) ; x5, x6, x7, x8, x9, x10 (AAAAAA), и теперь попытайтесь найти одну субпоследовательность в другой. Не получается. А вот если увеличить последовательность на один символ то получится. Например: ABBBAAAAAABA раскладывается на субпоследовательности x1, x2 (AB) ; x2, x3, x4 (BBB) ; x3, x4, x5, x6 (BBAA) ; x4, x5, x6, x7, x8 (BAAAA) ; x5, x6, x7, x8, x9, x10 (AAAAAA) ; x6, x7, x8, x9, x10, x11, x12 (AAAAABA) и последовательность x1, x2 (AB) входит в состав последовательности x6, x7, x8, x9, x10, x11, x12 (AAAAABA). Можете попробовать сами составить какую-нибудь другую последовательность из двух видов символов так чтобы она была "правильной", и вы убедитесь, что сделать ее длинее 11 символов у вас не получится. Ну а если мы будем использовать три вида символов, то на первый взгляд может показаться, что длина возможных "правильных последовательностей" неограничена, но это не так, просто функция уже в полной мере проявляет свой рост и BST(3) > 2[7198]158389. А уже BST(4) > 3[5,2[187195]187196]3 - что намного больше Числа Грэма. В конечном итоге скорость роста функции оценивается так: fωω+1(n) > BST(n) > fωω(n).[152]
Возвращаемся к нотациям. Уже знакомый нам по первой части американский математик Джонатан Бауэрс, глядя на Цепную нотацию Конвея, решил что из-за правила обрыва, когда например, a→b→1→d = a→b, эта нотация растет не так быстро как могла бы. Однако если правило обрыва убрать, то тогда правило рекурсии, в соответствии с которым: a→b→c→d = a→b→(a→b→c-1→d)→d-1, начнет бесконечно уменьшать аргумент c в отрицательные значения, что во-первых запрещено по правилам нотации, а во-вторых тогда возникнет бесконечная петля при вычислении числа. Поэтому Бауэрс решил, что это правило необходимо заменить так чтобы единицы в середине цепи не приводили бы к ее сокращению, а тоже участвовали бы в рекурсии. Для этого он придумал небольшую систему исключений, которая срабатывает вместо правила обрыва. Так же ему пришлось немного изменить правило рекурсии. Но обо всем по порядку. Прежде всего он изменил форму записи нотации, его аргументы записываются в фигурных скобках через запятую: {a,b,c,d,e,...}. Такую запись он назвал массивом, аргументы этой записи тоже получили особое название, у него они называются вхождениями (entries). Сама нотация стала называться массивной. Особую роль в его нотации выполняют первые два вхождения, у них тоже есть особые названия, первое называется база (a), второе - итератор (b). И правило рекурсии теперь срабатывает только на следующем вхождении после итератора (c), то есть только так: {a,b,c,d,e,...} = {a,{a,b-1,c,d,e,...},c-1,d,e,...}. Если бы в нотации Бауэрса действовало правило обрыва, то подобное изменение правила рекурсии сделало бы бессмысленным наличие всех остальных вхождений после третьего, потому что как только рекурсия дошла бы до стадии {a,b,1,d,e,...}, то все остальные вхождения просто отбросились бы, и тогда сила нотации была бы такая же как у обычного гипероператора. Ну а без правила обрыва второе и третье вхождения (b и с) по-прежнему бы уходили в отрицательные значения, и процесс вычисления так же бы зависал. Для этого и был придуман процесс исключений, чтобы заставить единцы рекурсировать, а не просто обрезать массив. Процесс исключений запускается если второе или третье вхождение (b или с) оказывается равным единице. В этом случае проверяется следующее вхождение, если и оно равно единице, то проверяется следующее за ним вхождение, и так пока не встретится вхождение, которое не будет равно единице. Тогда оно уменьшается на единицу, предыдущая единица становится итератором (b), а все единицы перед ней, и в том числе сам итератор (b), заменяются на значение базы (a). Например: {a,b,1,1,1,1,1,h} = {a,a,a,a,a,a,b,h-1}. С такой системой исключений вычисление нотации больше не будет зависать, а самое главное, теперь единицы будут работать на усиление рекурсии. Запись, в которой в массиве после итератора (b) стоит n единиц перед последним вхождением равным двум: {a,b,1,1,...,2}, теперь по силе становится почти аналогична раскрытию уровня в Расширенной цепной нотации (a→nb). И на самом деле, она даже сильнее, но в этом будем разбираться после изучения сравнительных примеров, которые я привожу сразу после строго формального определения массивной нотации в Приложении №10, с которым так же рекомендую каждому детально ознакомиться.
Линейная масcивная нотация (Linear array notation)
Определение:
{a,b,c,…,z} - массивная запись числа.
a b c ... z - вхождения (натуральные числа, больше 0).
“,” - запятая (символ ASCII=44) разделяет вхождения.
“{” , “}” - фигурные скобки (символ ASCII=123 и ASCII=125) указывают границы массива.
вхождение a - база.
вхождение b - итератор.
Правила:
Правило 1: (Правило базы - если в массиве два вхождения)
{a,b} = ab
Правило 2: (Правило хвоста - если последнее вхождение равно 1)
{#,1} = {#}
Правило 3: (Правило рекурсии - если 2-е и 3-е вхождение не равно 1)
{a,b,c #} = {a,{a,b-1,c #},c-1 #}
где “#” - какая-то часть массива (может включать вхождения, разделенные с запятыми, но также может быть пустой).
Процесс:
Циклично и последовательно проверяем выполнение 3-х приведенных выше правил, пока не выполнится первое правило.
Если ни одно из 3-х приведенных выше правил не применяется, то запускается процесс исключений.
Начинаем с 3-ого вхождения:
Случай A: Если вхождение равно 1, тогда переходим к следующему вхождению.
Случай B: Если вхождение не равно 1, тогда:
1) изменяем
“1,n” (это вхождение и предыдущую единицу) на
“b,n-1”, где b - итератор.
2) изменяем все предыдущие вхождения на a, где a - база.
3) закончить и перейти к проверке правил.
Частные случаи:
{a,b,с} = a↑сb = a→b→c
{a,b,1,2} = a↑ba = a→a→b
{a,b,с,d} = a→a→... b→c - где число вхождений "a→" равно d
{a,a,a,a-2} = a→2a = a→a→... - где число вхождений "a→" равно a
{a,b,1,1,2} = a→a→... - где число вхождений "a→" равно b+2
{a,b,1,2} = {a,a,b}
{a,b,c,d} = {a,{a,...{a,a,c-1,d}..,c-1,d},c-1,d} - где b-1 вложений
{a,b,1,d+1} = {a,a,b,d}
{a,b,1,1,2} = {a,a,a,b}
{a,b,c,d,e} = {a,{a,{a,a,c-1,d,e},c-1,d,e},c-1,d,e} - где b-1 вложений
{a,b,1,d+1,e} = {a,a,b,d,e}
{a,b,1,1,e+1} = {a,a,a,b,e}
{a,b,1,1,1,2} = {a,a,a,a,b}
и т.д.
Первоначальное авторство: Джонатан Бауэрс, 2002 год.
[153]
Последующая модификация: Крис Бёрд, 2012 год.
[154]
Последующая модификация: Hypcos, 2015 год.
[155]
приложение 10 (Линейная массивная нотация)
f3(n) > n[3]n = n↑n = n→n = {n,n} = nn
f4(n) > n[4]n = n↑↑n = n→n→2 = {n,n,2} = {n,{n,...{n}...}} n-1 вложений
f5(n) > n[5]n = n↑↑↑n = n→n→3 = {n,n,3} = {n,{n,...{n}...,2},2} n-1 вложений
f6(n) > n[6]n = n↑↑↑↑n = n→n→4 = {n,n,4} = {n,{n,...{n}...,3},3} n-1 вложений
fω(n) > n[n+2]n = n↑nn = n→n→n = {n,n,1,2} = {n,n,n}
fω+1(n) > n[3,n]n = n→n→n→2 = {n,n,2,2} = {n,n,{n,n,...{n,n,n}...}} n-1 вложений
fω+2(n) > n[3,nn,n]n = n→n→n→3 = {n,n,3,2} = {n,{n,...{n,n,2,2}...,2,2}2,2} n-1 вложений
fω+3(n) > n[3,nn,nn,n]n = n→n→n→4 = {n,n,4,2} = {n,{n,...{n,n,3,2}...,3,2}3,2} n-1 вложений
fω×2(n) > n[[n]]n ≈ n→n→n→n = {n,n,1,3} = {n,n,n,2}
fω×2+1(n) > n[[n,n]]n ≈ n→n→n→n→2 = {n,n,2,3} = {n,n,{n,n,...{n,n,n,2}...,2},2} n-1 вложений
fω×2+2(n) > n[[n,n,n]]n ≈ n→n→n→n→3 = {n,n,3,3} = {n,{n,...{n,n,2,3}...,2,3}2,3} n-1 вложений
fω×2+3(n) > n[[n,n,n,n]]n ≈ n→n→n→n→4 = {n,n,4,3} = {n,{n,...{n,n,3,3}...,3,3}3,3} n-1 вложений
fω×3(n) > n[[[n]]]n ≈ n→n→n→n→n = {n,n,1,4} = {n,n,n,3}
fω×3+1(n) > n[[[n,n]]]n ≈ n→n→n→n→n→2 = {n,n,2,4} = {n,n,{n,n,...{n,n,n,3}...,3},3} n-1 вложений
fω×3+2(n) > n[[[n,n,n]]]n ≈ n→n→n→n→n→3 = {n,n,3,4} = {n,{n,...{n,n,2,4}...,2,4}2,4} n-1 вложений
fω×3+3(n) > n[[[n,n,n,n]]]n ≈ n→n→n→n→n→4 = {n,n,4,4} = {n,{n,...{n,n,3,4}...,3,4}3,4} n-1 вложений
fω×4(n) > n[[[[n]]]]n ≈ n→n→n→n→n→n = {n,n,1,5} = {n,n,n,4}
fω×5(n) > n[[[[[n]]]]]n ≈ n→n→n→n→n→n→n = {n,n,1,6} = {n,n,n,5}
fω2(n) > n→2n ≈ {n,n,1,1,2} = {n,n,n,n} = n→n→n→n→n→n→...n раз
fω2+1(n) > n→2n→2 ≈ {n,n,2,1,2} = {n,n,n,{n,n,n,...{n,n,n,n}...}} n-1 вложений
fω2+2(n) > n→2n→3 ≈ {n,n,3,1,2} = {n,{n,...{n,n,2,1,2}...,2,1,2}2,1,2} n-1 вложений
fω2+3(n) > n→2n→4 ≈ {n,n,4,1,2} = {n,{n,...{n,n,3,1,2}...,3,1,2}3,1,2} n-1 вложений
fω2+ω(n) > n→2n→n ≈ {n,n,1,2,2} = {n,n,n,1,2}
fω2+ω+1(n) > n→2n→n→2 ≈ {n,n,2,2,2} = {n,n,{n,n,...{n,n,n,1,2}...,1,2},1,2} n-1 вложений
fω2+ω+2(n) > n→2n→n→3 ≈ {n,n,3,2,2} = {n,{n,...{n,n,2,2,2}...,2,2,2},2,2,2} n-1 вложений
fω2+ω×2(n) > n→2n→n→n ≈ {n,n,1,3,2} = {n,n,n,2,2}
fω2+ω×3(n) > n→2n→n→n→n ≈ {n,n,1,4,2} = {n,n,n,3,2}
fω2×2(n) > n→2n→2n ≈ {n,n,1,1,3} = {n,n,n,n,2}
fω2×2+1(n) > n→2n→2n→2 ≈ {n,n,2,1,3} = {n,n,n,{n,n,n,...{n,n,n,n,2}...,2},2} n-1 вложений
fω2×2+2(n) > n→2n→2n→3 ≈ {n,n,3,1,3} = {n,{n,...{n,n,2,1,2}...,2,1,2}2,1,2} n-1 вложений
fω2×2+ω(n) > n→2n→2n→n ≈ {n,n,1,2,3} = {n,n,n,1,3}
fω2×2+ω+1(n) > n→2n→2n→n→2 ≈ {n,n,2,2,3} = {n,n,{n,n,...{n,n,n,1,3}...,1,3},1,3} n-1 вложений
fω2×2+ω×2(n) > n→2n→2n→n→n ≈ {n,n,1,3,3} = {n,n,n,2,3}
fω2×3(n) > n→2n→2n→2n ≈ {n,n,1,1,4} = {n,n,n,n,3}
fω2×4(n) > n→2n→2n→2n→2n ≈ {n,n,1,1,5} = {n,n,n,n,4}
fω3(n) > n→3n ≈ {n,n,1,1,1,2} = {n,n,n,n,n}
fω3+1(n) > n→3n→2 ≈ {n,n,2,1,1,2} = {n,n,n,n,{n,n,n,n,...{n,n,n,n,n}...}} n-1 вложений
fω3+ω(n) > n→3n→n ≈ {n,n,1,2,1,2} = {n,n,n,1,1,2}
fω3+ω2(n) > n→3n→2n ≈ {n,n,1,1,2,2} = {n,n,n,n,1,2}
fω3×2(n) > n→3n→3n ≈ {n,n,1,1,1,3} = {n,n,n,n,n,2}
fω3×3(n) > n→3n→3n→3n ≈ {n,n,1,1,1,4} = {n,n,n,n,n,3}
fω4(n) > n→4n ≈ {n,n,1,1,1,1,2} = {n,n,n,n,n,n}
fω5(n) > n→5n ≈ {n,n,1,1,1,1,1,2} = {n,n,n,n,n,n,n}
fωω(n) > n→nn ≈ {n,n,1,1,1,1,1,...n раз...2} = {n,n,n,n,n,n,...n раз...}
Как вы можете увидеть из приведенных выше примеров, по скорости роста массивная нотация сопоставима со скоростью роста Цепной нотации с расширением Хёрфорда. Однако начиная со второго уровня цепи совпадения с массивной нотацией становятся неточными, так же как это ранее было с расширенным гипероператором, который, начиная с двойного расширения, не в точности соотносился с Цепной нотацией. Дело в том, что массив {n,n,n,m} в точно эквивалентен цепи n→n→n→n→... из m+2 аргументов, в то время как цепь второго уровня n→2m эквивалентна лишь цепи из n→n→n→n→... из m аргументов. То есть получается, что {n,n,1,1,2} = {n,n,n,n} > n→2n. И так же как это было с расхожениями между расширенным гипероператором и цепной нотацией, данные расхождения между расширенной цепной нотацией и массивной нотацией в масштабах обычных человеческих чисел неимоверно велики. Но поскольку в сравнении с функциями быстрорастущей иерархии, обе нотации проигрывают (например, fω2(n) > {n,n,n,n} > n→2n), а более точного способа измерения их силы мы все равно не имеем, я так же взял на себя смелость поставить между ними знак приблизительного равенства. Но не только из-за этого небольшого расхождения массивную нотацию следует считать более сильной, к тому же как мы выяснили разница в масштабах функций быстрорастущей иерархии невелика. Дело в том, что расширенная цепная нотация Хёрфорда сложнее поскольку в ней участвует две группы аргументов: собственно вхождения цепи и уровни цепи. А как мы выяснили еще в начале этой главы, более сильной следует считать функцию использующую меньше аргументов. Так же из-за того что уровни цепи не могут быть расставлены в порядке возрастания это ограничивает силу рекурсии, и несмотря на то что уровни цепи Хёрфорда это уже расширение, а не модификация нотации, все равно такое расширение не превосходит метод Бауэрса. Тем не менее, мы можем воспользоваться методом Хёрфорда и расширить массивную нотацию, добавив группу аргументов, которые будут символизировать уровень разделителей в массиве, что собственно и сделал сам Бауэрс.
Но перед там как разобрать этот метод, я забегая вперед, хочу отметить, что Бауэрс создал свою нотацию в 2002 году и после этого до 2008 года неоднократно расширял ее, после чего в 2012 году знамя подхватил английский математик Крис Бёрд, причем, начиная с определенного момента, он пошел своим путем и к 2014 сделал нотацию еще сильнее. В 2015 году китайский математик известный под псевдонимом Hypcos, взяв наработки Бёрда усилил нотацию до невероятных пределов. Я не буду рассматривать весь путь развития, которым прошла массивная нотация, и не буду детально сравнивать рекурсии из разных семейств, а сразу перейду к расширениям Hypcos, которые сам он назвал Strong Array Notation (SAN), что переводится как Сильная массивная нотация, именно это семейство расширений мы и будем рассматривать на протяжении большей части книги. Массивную нотацию без всяких расширений принято называть Линейной массивной нотацией. Ниже в Таблице №17 я привожу все нотации, которые мы уже рассмотрели, а так же все семейства массивных нотаций, располагая их по силе, и измеряя эту силу функциями быстрорастущей иерархии (пусть пока вам вероятно не понятен масштаб ординалов, что в них подставлены, но вы всегда можете вернуться к этой таблице позже). Одинаковым цветом закрашены нотации, которые в сущности имеют одинаковые правила вычисления, и могут отличаться только записью или минимальными тонкостями при вычислении.
| FGH |
Стандартные нотации |
Кнут / Конвей / Хёрфорд |
Бауэрс[153] |
Бёрд[156] |
SAN[157] |
| f3(n) |
Десятичная нотация |
Стрелочная нотация |
Линейная массивная нотация |
Линейная массивная нотация |
Линейная массивная нотация |
| Логарифмическая нотация |
| Степенная башня |
| f4(n) |
Тетрационная башня |
| f5(n) |
Пентационная башня |
| fω(n) |
Гипероператор |
| fω2(n) |
Расширенный гипероператор |
Цепная нотация |
| fωω(n) |
Расширенная цепная нотация |
| fωωω(n) |
Многомерная массивная нотация |
Многомерная массивная нотация |
Расширенная массивная нотация |
| fωωωω(n) |
Гипермерная массивная нотация |
Гипермерная массивная нотация |
| fε0(n) |
Вложенная массивная нотация |
Вложенная массивная нотация |
| fεω(n) |
Гипер-операционная массивная нотация |
Вложено-вложенная массивная нотация |
Примитивно расширяющаяся массивная нотация |
| fφ(ω,0)(n) |
Гипер-вложенная массивная нотация |
Иерархическая гипер-вложенная массивная нотация |
Первично расширяющаяся массивная нотация |
| fψ(ΩΩω)(n) |
Массивно-операционная массивная нотация |
Вложенная гипер-вложенная массивная нотация |
| fψ(ΩΩΩ)(n) |
Массивно-массивная нотация |
| fψ(ΩΩΩ×ω)(n) |
Легионная нотация |
| fψ(ΩΩΩω)(n) |
| fψ(εΩ+1)(n) |
Вложенная индексная массивная нотация |
| fψ(Ωω)(n) |
Множественно расширяющаяся массивная нотация |
| fψ(ΩΩ)(n) |
Вложенная иерархическая гипер-вложенная массивная нотация |
Первично нисходящая массивная нотация |
| fψ(ψI(ω,0)(0))(n) |
| fCCCCCΩ20CΩ2CCΩ2Ω20Ω200(n) |
Расширенная нисходящая массивная нотация |
| fCCCC0CΩ2CΩ2CCΩ2Ω20Ω200(n) |
Расширяющаяся нисходящая массивная нотация |
| fCCCCC0CΩ2CΩ2CCΩ2Ω20CΩ2CΩ2CCΩ2Ω20Ω200(n) |
Вторично нисходящая массивная нотация |
| fCCCCC0Ω2CCΩ2Ω20Ω200(n) |
Множественно нисходящая массивная нотация |
таб.17 (Иерархия нотаций)
Итак, теперь мы точно знаем по какому пути расширений идти, но так или иначе, все пути начинаются с метода Хёрфорда по добавлению уровня разделителя. В цепной нотации разделителем выступала стрелка, и добавив к ней уровень, мы получали следующую рекурсию: a→2b = a→a→a→a→... длиной b. В Линейной массивной нотации разделителем выступает запятая, которую мы иначе запишем так "(1)", что значит разделитель первого уровня. Тогда запись {n,n,n,n,...} будет выглядеть так {n(1)n(1)n(1)n(1)...}. Теперь внимание, согласно первому правилу массивной нотации получается: {a(1)b} = {a(2)b} = {a(n)b} = ab, потому что первое правило ничего не говорит о разделителях, но всегда превращает массив, состоящий лишь из двух вхождений, в операцию возведения в степень. Однако в Расширенной цепной нотации первое правило было изменено, и срабатывало только в случае, если стрелка между аргументами была первого уровня. Мы же изменять его не будем. Правило базы необходимо оставить в неизменном виде, потому что процесс исключений, по которому и работают рекурсии, начинается с третьего вхождения, а значит алгоритм вычисления нотации никогда не доберется до раскрытия разделителей более высоких уровней стоящих перед вторым вхождением, что сделает нотацию неработоспособной. Функцию расширения точно так же может взять на себя второй разделитель и тогда получится что: {n,m(2)2} = {n,n,n,n,n,...} где m+1 вхождение = {n,n,1,1,1,...,2} где m-1 единиц. Как вы заметили, несмотря на то, что расширение начинается с третьего вхождения, принцип рекурсии остался столь же силен и схож с "n→2n". Для получения аналога рекурсии “n→2n→2 = n→2n→(n→2n→(n→2n→...)) - где n-1 вложений” в массивной нотации мы должны записать массив так: {n,m,2(2)2}, и по правилам он будет рекурсивно раскладываться на {n,{n,{n,{...}(2)2}(2)2}(2)2} - где m-1 вложений, что примерно соответствует рекурсии “{n,n,1,1,1,...,2} - где число единиц равно {n,n,1,1,1,...,2} - где число единиц равно {n,n,1,1,1,...,2} - где ... и так m-1 раз”, или так же эту рекурсию можно выразить иначе: “{n,n,n,n,n,...} - где число вхождений равно {n,n,n,n,n,...} - где число вхождений равно {n,n,n,n,n,...} - где ... и так m-1 раз”. Как видите, мы можем располагать разделители меньшего уровня перед разделителями бо́льшего уровня, что запрещено делать по правилам Расширенной цепной нотации, и так же, как это было с возможностью располагать единицы в массиве спереди, данная возможность тоже в итоге сделает нашу рекурсию намного сильнее. Ну а дальше продолжаем в стиле Линейной массивной нотации: {n,n,n(2)2} = {n,n,1,2(2)2}, затем {n,m,2,2(2)2} = {n,n,{n,n,{n,n,...(2)2}(2)2}(2)2} - где m-1 вложений. И так до тех пор, пока: {n,m(2)3} = {n,n,n,n,n,...(2)2} - где m+1 вхождение = {n,n,1,1,1,...,2(2)2} где m-1 единиц.
Вот только сейчас, пройдя столько рекурсий, мы сдвинули вхождение после разделителя второго уровня с мертвой точки. После чего мы можем продолжить усиливать рекурсии по той же схеме: {n,m,2(2)3} = “{n,{n,{n,{...}(2)3}(2)3}(2)3} - где m-1 вложений” = “{n,n,1,1,1,...(2)2} - где число единиц равно {n,n,1,1,1,...(2)2} - где число единиц равно {n,n,1,1,1,...(2)2} - где ... и так m-1 раз” = “{n,n,n,n,n,...(2)2} - где число вхождений равно {n,n,n,n,n,...(2)2} - где число вхождений равно {n,n,n,n,n,...(2)2} - где ... и так m-1 раз”. Затем переходим к {n,m(2)4} = {n,n,n,n,n,...(2)3} - где m+1 вхождение = {n,n,1,1,1,...,2(2)3} где m-1 единиц, потом сразу прыгаем к {n,n(2)n} = {n,n(2)1,2}. Ну а после разделителя второго уровня наращивать рекурсии становится уже непросто, потому что рекурсия: “{n,n(2){n,n(2){n,n(2)...}}} - где m-1 вложений” эквивалентна только {n,m,2(2)1,2}. И чтобы получить {n,m(2)2,2} необходимо сделать так: {n,n,n,n,n,...(2)1,2} - где m+1 вхождение = {n,n,1,1,1,...,2(2)1,2} где m-1 единиц. Теперь так же продвигаемся дальше по схеме Линейной массивной нотации, только накручивая рекурсии уже после разделителя второго уровня: {n,n(2)n,n} = {n,n(2)1,1,2}, {n,n(2)n,n,n} = {n,n(2)1,1,1,2}, и т.д. Будем делать это наращивание рекурсий до тех пор, пока: {n,m(2)1(2)2} = {n,n(2)n,n,n,n,n,...} - где m+2 вхождения = {n,n(2)1,1,1,...,2} где m единиц, и вот только лишь сейчас появляется второй разделитель второго уровня. Теперь нам придется пройти сквозь еще один, уже в два раза более мощный, круговорот рекурсий, чтобы от выражения {n,m(2)1(2)2} добраться до выражения {n,m(2)1(2)1(2)2}, ведь “{n,n(2)n,n,n,n,n,...} - где число вхождений после "(2)" равно {n,n(2)n,n,n,n,n,...} - где число вхождений после "(2)" равно {n,n(2)n,n,n,n,n,...} - где ... и так m-1 раз” - это лишь {n,m,2(2)1(2)2}.
Дальше схема уже становится очевидной и схожей с методом Хёрфорда по увеличению уровня разделителей: {n,m(3)2} = {n,n(2)1(2)1(2)1(2)...2} - где m-1 единиц, ну или в общем случае получается что {n,m(k+1)2} = {n,n(k)1(k)1(k)1(k)...2} - где m-1 единиц. Как вы могли убедиться возможность располагать разделители меньшего уровня перед разделителями бо́льшего уровня открыла нам новые возможности для рекурсирования. Однако чтобы нотация корректно работала для всех допустимых способов записи, необходимо ввести еще одно правило, назовем его правилом сокращения (сам Hypcos его никак не называет). Звучит оно следующим образом, если перед разделителем бо́льшего уровня стоит разделитель меньшего уровня, а между ними вхождение равное единице, то разделитель меньшего уровня и единица после него убираются, например: {n,m(2)1(3)2} = {n,m(3)2}. Не переживайте в отличие от правила обрыва, данное правило совсем не ослабит нотацию, это просто технический момент, без него в некоторых случаях (например: {n,m,1,2(2)2}) массивы бы вычислялись бесконечно, и нотация оказалась бы нерабочей. Еще я пока не упомянул, про составные разделители, которые сделают нотацию еще сильнее, и для сравнения их уровня нам уже потребуется специальный алгоритм. Но предлагаю пока остановится на рубеже {n,n(n)n} и ознакомиться с полными правилами Расширенной массивной нотации, не вдаваясь в подробности о том, что такое составной разделитель. Заметьте, что этот рубеж еще не является ее пределом, но нам пока необходимо освоиться на нем перед тем как идти дальше, для этого внимательно изучите сравнения выражений с функциями быстрорастущей иерархии.
Расширенная масcивная нотация (Extended array notation)
Определение:
Действительны все определения Linear array notation.
(m) это разделитель, в котором m - натуральное число больше нуля.
(#Sm) это разделитель, в котором m - натуральное число больше нуля, S - это разделитель, и # это такая строка, что (#) это разделитель.
“(” , “)” - скобки (символ ASCII=40 и ASCII=41) указывают границы разделителя.
{a,b} это массив, в котором a и b - натуральные числа, больше нуля (a - база, b - итератор).
{#Sm} это массив, в котором m - натуральное число больше нуля, S - это разделитель, и # это такая строка, что {#} это массив.
(m1S1m2S2…mk-1Sk-1mk) - составной разделитель, где m
i это натуральное число больше нуля, S
i это разделитель или составной разделитель;
k ≥ 1.
Если k=1, тогда разделитель имеет вид (m).
Простейший разделитель такого вида (1) это “,” - запятая, его краткая запись.
{a,b,c,…,z} = {a(1)b(1)c(1)…(1)z}
Таким образом, массивная запись числа, это вхождения разделенные разделителями.
Причем вхождения бывают как в массиве, так и в разделителях.
В массиве
{m1S2m2S2…mk-1Sk-1mk}, все вхождения m
i это базовый слой, а все разделители S
i это слой 1.
Если разделитель
(m1S1m2S2…mk-1Sk-1mk) это слой n, тогда все разделители S
i это слой n+1.
Чтобы иметь возможность сравнивать разделители вводится понятие уровня разделителя.
Уровень разделителей:
Уровень - это свойство разделителей, которое позволяет сравнить их с другими разделителями, используя «<», «>» и «=».
Уровень записывается следующим образом: уровень A это lv(A).
Массивы тоже имеют уровень, у них он всегда одинаковый и наинизший.
Одинаковые разделители имеют одинаковый уровень.
Сравнение уровней:
Чтобы сравнить уровни двух разных разделителей A и B, необходимо выполнить следующие шаги:
1) Применять “правило хвоста” к A и B до тех пор, пока “правило хвоста” больше не может применяться.
2a) Представим разделитель A в виде (a
1A
1a
2A
2…a
k-1A
k-1a
k) - составного разделителя,
где a
i это натуральное число больше нуля, A
i это разделитель или составной разделитель, k ≥ 1.
2b) Представим разделитель B в виде (b
1B
1b
2B
2…b
l-1B
l-1b
l) - составного разделителя,
где b
i это натуральное число больше нуля, B
i это разделитель или составной разделитель, l ≥ 1.
3) Если k = 1 и l > 1 , тогда lv(A) < lv(B); если k > 1 и l = 1 , тогда lv(A) > lv(B); если k = l = 1 , переходим к шагу 4; если k > 1 и l > 1 , переходим к шагам с 5 по 10.
4) Если a
1 < b
1, тогда lv(A) < lv(B); если a
1 > b
1, тогда lv(A) > lv(B); если a
1 = b
1, тогда lv(A) = lv(B).
5a) Пусть M(A)={i∈{1,2,...,k-1}|∀j∈{1,2,...,k-1}(lv(A
i) ≥lv(A
j))} - множество с номерами наивысших разделитей.
5a) Пусть M(B)={i∈{1,2,...,k-1}|∀j∈{1,2,...,k-1}(lv(B
i) ≥lv(B
j))} - множество с номерами наивысших разделитей.
6) Если lv(A
max(M(A))) < lv(B
max(M(B))) , тогда lv(A) < lv(B); если lv(A
max(M(A))) > lv(B
max(M(B))) , тогда lv(A) > lv(B); иначе переходим к шагу 7.
7) Если |M(A)| < |M(B)| , тогда lv(A) < lv(B); если |M(A)| > |M(B)| , тогда lv(A) > lv(B); иначе переходим к шагу 8.
8) Пусть A = (#
1 A
max(M(A)) #
2) и B = (#
3 B
max(M(B)) #
4) ,
где “#
i” - какие-то строки вхождений и разделителей, также могут быть пустыми.
9) Если lv((#
2)) < lv((#
4)) , тогда lv(A) < lv(B); если lv((#
2)) > lv((#
4)) , тогда lv(A) > lv(B); иначе переходим к шагу 10.
10) Если lv((#
1)) < lv((#
3)) , тогда lv(A) < lv(B); если lv((#
1)) > lv((#
3)) , тогда lv(A) > lv(B); если lv((#
1)) = lv((#
3)) , тогда lv(A) = lv(B).
Правила:
Правило 1: (Правило базы - если в массиве два вхождения)
{a S b} = {a,b} = ab
Правило 2: (Правило хвоста - если последнее вхождение массива или разделителя равно 1)
{# S 1} = {#} или (# S 1) = (#)
Правило 3: (Правило рекурсии - если 2-е и 3-е вхождение не равно 1)
{a,b,c #} = {a,{a,b-1,c #},c-1 #}
Правило 4: (Правило сокращения - если lv(S) < lv(S
+), для массива или разделителя) {# S 1 S
+ #
+} = {# S
+ #
+} или (# S 1 S
+ #
+) = (# B #
+)
“#” и “#
+” - какие-то строки вхождений и разделителей, также могут быть пустыми.
“S” и “S
+” - какие-то разделители.
Процесс:
Циклично и последовательно проверяем выполнение 4-х приведенных выше правил, пока не выполнится первое правило.
Если ни одно из 4-х приведенных выше правил не применяется, то запускается процесс исключений.
Начинаем с 3-ого вхождения:
Случай A: Если вхождение равно 1, тогда переходим к следующему вхождению.
Случай B: Если вхождение не равно 1, тогда смотрим на предыдущий элемент:
Случай B1: Если это запятая “,” тогда:
1) изменяем “1,n” (это вхождение и предыдущую единицу)
на “b,n-1”, где b - итератор.
2) изменяем все предыдущие вхождения в базовом слое на a, где a - база.
3) закончить и перейти к проверке правил.
Случай B2: Если это разделитель “S”, не являющийся запятой, тогда:
1)
изменяем “S n” на“S 2 S n-1”.
2) переходим к первому вхождению в первом из S.
Случай B3: Если это открывающаяся скобка “(” тогда:
1) изменяем разделитель “
(n #)” на строку S
b, где b это итератор,
S1 = “(n-1 #)” и Si+1 = “Si 1 (n-1 #)”.
2) закончить и перейти к проверке правил.
Первоначальное авторство: Джонатан Бауэрс, 2008 год.
[153]
Последующая модификация: Крис Бёрд, 2013 год.
[158][159][160]
Последующая модификация: Hypcos, 2015 год.
[161]
приложение 11 (Расширенная массивная нотация)
Перед тем как приводить сравнения я бы хотел напомнить некоторые особенности, характерные для операций со степенью, которые должны быть вам знакомы из школьной алгебры седьмого класса: an×a = an+1 и an×an = (an)2 = an×2, которые так же применимы и для ординальной арифметики: ωn×ω = ωn+1 и ωn×ωn = (ωn)2 = ωn×2. Иногда эти очевидные формулы забываются, но если держать их в голове, то вы быстрее сможете получать следующие преобразования:
ωω+1 = ωω×ω;
ωω+2 = ωω×ω×ω;
ωω×2 = (ωω)2 = ωω×ωω;
ωω×2+1 = ωω×ωω×ω;
ωω×3 = ωω×ωω×ωω;
ωω2 = ωω×ωω×ωω×ωω×... - ω раз;
ωωω+1 = ωωω×ω;
ωωω×2 = (ωωω)2 = ωωω×ωωω;
ωωω+1 = ωωω×ω
и т.д.
Они пригодятся вам для понимания рекурсий в функциях быстрорастущей иерархии, чтобы их было проще сопоставлять с рекурсиями Расширенной массивной нотации.
fωω(n) > {n,n(2)2} = {n,n,1,1,1,...n-1 раз...2} = {n,n,n,n,n,...n-1 раз...}
fωω+1(n) > {n,n,2(2)2} = {n,{n,...{n,n(2)2}...(2)2}(2)2} n-1 вложений
fωω+2(n) > {n,n,3(2)2} = {n,{n,...{n,n(2)2}...,2(2)2},2(2)2} n-1 вложений
fωω+ω(n) > {n,n,1,2(2)2} = {n,n,n(2)2}
fωω+ω+1(n) > {n,n,2,2(2)2} = {n,n,{n,n,...{n,n,n,(2)2}...(2)2}(2)2} n-1 вложений
fωω+ω×2(n) > {n,n,1,3(2)2} = {n,n,n,2(2)2}
fωω+ω×2+1(n) > {n,n,2,3(2)2} = {n,n,{n,n,...{n,n,n,2(2)2}...2(2)2}2(2)2} n-1 вложений
fωω+ω×3(n) > {n,n,1,4(2)2} = {n,n,n,3(2)2}
fωω+ω2(n) > {n,n,1,1,2(2)2} = {n,n,n,n(2)2}
fωω+ω2+1(n) > {n,n,2,1,2(2)2} = {n,n,n,{n,n,n,...{n,n,n,(2)2}...(2)2}(2)2} n-1 вложений
fωω+ω2+ω(n) > {n,n,1,2,2(2)2} = {n,n,n,1,2(2)2}
fωω+ω2×2(n) > {n,n,1,1,3(2)2} = {n,n,n,n,2(2)2}
fωω+ω3(n) > {n,n,1,1,1,2(2)2} = {n,n,n,n,n(2)2}
fωω×2(n) > {n,n(2)3} = {n,n,1,1,1,...n-1 раз...2(2)2} = {n,n,n,n,n,...n-1 раз...(2)2}
fωω×2+1(n) > {n,n,2(2)3} = {n,{n,...{n,n(2)3}...(2)3}(2)3} n-1 вложений
fωω×2+ω(n) > {n,n,1,2(2)3} = {n,n,n(2)3}
fωω×2+ω2(n) > {n,n,1,1,2(2)3} = {n,n,n,n(2)3}
fωω×2+ω3(n) > {n,n,1,1,1,2(2)3} = {n,n,n,n,n(2)3}
fωω×3(n) > {n,n(2)4} = {n,n,1,1,1,...n-1 раз...2(2)3} = {n,n,n,n,n,...n-1 раз...(2)3}
fωω+1(n) > {n,n(2)1,2} = {n,n(2)n}
fωω+1+1(n) > {n,n,2(2)1,2} = {n,n(2){n,n(2)...{n,n(2)n}...}} n-1 вложений
fωω+1+ω(n) > {n,n,1,2(2)1,2} = {n,n,n(2)1,2}
fωω+1+ω2(n) > {n,n,1,1,2(2)2} = {n,n,n,n(2)2}
fωω+1+ω3(n) > {n,n,1,1,1,2(2)2} = {n,n,n,n,n(2)1,2}
fωω+1+ωω(n) > {n,n(2)2,2} = {n,n,1,1,1,...n-1 раз...2(2)1,2} = {n,n,n,n,n,...n-1 раз...(2)1,2}
fωω+1+ωω×2(n) > {n,n(2)3,2} = {n,n,1,1,1,...n-1 раз...2(2)2,2} = {n,n,n,n,n,...n-1 раз...(2)2,2}
fωω+1×2(n) > {n,n(2)1,3} = {n,n(2)n,2}
fωω+1×3(n) > {n,n(2)1,4} = {n,n(2)n,3}
fωω+2(n) > {n,n(2)1,1,2} = {n,n(2)n,n}
fωω+2+ωω(n) > {n,n(2)2,1,2} = {n,n,1,1,1,...n-1 раз...2(2)1,1,2} = {n,n,n,n,n,...n-1 раз...(2)1,1,2}
fωω+2+ωω+1(n) > {n,n(2)1,2,2} = {n,n(2)n,1,2}
fωω+2×2(n) > {n,n(2)1,1,3} = {n,n(2)n,n,2}
fωω+3(n) > {n,n(2)1,1,1,2} = {n,n(2)n,n,n}
fωω×2(n) > {n,n(2)1(2)2} = {n,n(2)1,1,1,...n раз...2} = {n,n(2)n,n,n,...n раз...}
fωω×2+1(n) > {n,n,2(2)1(2)2} = {n,{n,...{n,n(2)1(2)2}...(2)1(2)2}(2)1(2)2} n-1 вложений
fωω×2+ωω(n) > {n,n(2)2(2)2} = {n,n,1,1,1,...n-1 раз...2(2)1(2)2} = {n,n,n,n,n,...n-1 раз...(2)1(2)2}
fωω×2+ωω+1(n) > {n,n,2(2)2(2)2} = {n,{n,...{n,n(2)2(2)2}...(2)2(2)2}(2)2(2)2} n-1 вложений
fωω×2+ωω×2(n) > {n,n(2)3(2)2} = {n,n,1,1,1,...n-1 раз...2(2)2(2)2} = {n,n,n,n,n,...n-1 раз...(2)2(2)2}
fωω×2+ωω+1(n) > {n,n(2)1,2(2)2} = {n,n(2)n(2)2}
fωω×2+ωω+1+1(n) > {n,n,2(2)1,2(2)2} = {n,n(2){n,n(2)...{n,n(2)n(2)2}...(2)2}(2)2} n-1 вложений
fωω×2+ωω+1+ωω(n) > {n,n(2)2,2(2)2} = {n,n,1,1,1,...n-1 раз...2(2)1,2(2)2} = {n,n,n,n,n,...n-1 раз...(2)1,2(2)2}
fωω×2+ωω+1×2(n) > {n,n(2)1,3(2)2} = {n,n(2)n,2(2)2}
fωω×2+ωω+2(n) > {n,n(2)1,1,2(2)2} = {n,n(2)n,n(2)2}
fωω×2×2(n) > {n,n(2)1(2)3} = {n,n(2)1,1,1,...n раз...2(2)2} = {n,n(2)n,n,n,...n раз...(2)2}
fωω×2+1(n) > {n,n(2)1(2)1,2} = {n,n(2)1(2)n}
fωω×2+1+1(n) > {n,n,2(2)1(2)1,2} = {n,n(2)1(2){n,n(2)1(2)...{n,n(2)1(2)n}...}} n-1 вложений
fωω×2+1+ωω(n) > {n,n(2)2(2)1,2} = {n,n,1,1,1,...n-1 раз...2(2)1(2)1,2} = {n,n,n,n,n,...n-1 раз...(2)1(2)1,2}
fωω×2+1+ωω×2(n) > {n,n(2)1(2)2,2} = {n,n(2)1,1,1,...n раз...2(2)1,2} = {n,n(2)n,n,n,...n раз...(2)1,2}
fωω×2+1×2(n) > {n,n(2)1(2)1,3} = {n,n(2)1(2)n,2}
fωω×2+2(n) > {n,n(2)1(2)1,1,2} = {n,n(2)1(2)n,n}
fωω×3(n) > {n,n(2)1(2)1(2)2} = {n,n(2)1(2)1,1,1,...n раз...2} = {n,n(2)1(2)n,n,n,...n раз...}
fωω×4(n) >{n,n(2)1(2)1(2)1(2)2} = {n,n(2)1(2)1(2)1,1,1,...n раз...2} = {n,n(2)1(2)1(2)n,n,n,...n раз}
fωω2(n) > {n,n(3)2} = {n,n(2)1(2)1(2)1(2)...n-1 раз...2}
fωω2+1(n) > {n,n,2(3)2} = {n,{n,...{n,n(3)2}...(3)2}(3)2} n-1 вложений
fωω2+ωω(n) > {n,n(2)2(3)2} = {n,n,1,1,1,...n-1 раз...2(3)2} = {n,n,n,n,n,...n-1 раз...(3)2}
fωω2+ωω+1(n) > {n,n(2)1,2(3)2} = {n,n(2)n(3)2}
fωω2+ωω×2(n) > {n,n(2)1(2)2(3)2} = {n,n(2)1,1,1,...n раз...2(3)2} = {n,n(2)n,n,n,...n раз...(3)2}
fωω2+ωω×2+1(n) > {n,n(2)1(2)3(3)2} = {n,n(2)1,1,1,...n раз...2(2)2(3)2} = {n,n(2)n,n,n,...n раз...(2)2(3)2}
fωω2+ωω×3(n) > {n,n(2)1(2)1(2)2(3)2} = {n,n(2)1(2)1,1,1,...n раз...2(3)2} = {n,n(2)1(2)n,n,n,...n раз...(3)2}
fωω2×2(n) > {n,n(3)3} = {n,n(2)1(2)1(2)1(2)...n-1 раз...2(3)2}
fωω2+1(n) > {n,n(3)1,2} = {n,n(3)n}
fωω2+ω(n) > {n,n(3)1(2)2} = {n,n(3)1,1,1,...n раз...2} = {n,n(3)n,n,n,...n раз...}
fωω2+ω×2(n) > {n,n(3)1(2)1(2)2} = {n,n(3)1(2)1,1,1,...n раз...2} = {n,n(3)1(2)n,n,n,...n раз...}
fωω2×2(n) > {n,n(3)1(3)2} = {n,n(3)1(2)1(2)1(2)...n раз...2}
fωω2×3(n) > {n,n(3)1(3)1(3)2} = {n,n(3)1(3)1(2)1(2)1(2)...n раз...2}
fωω2×4(n) > {n,n(3)1(3)1(3)1(3)2} = {n,n(3)1(3)1(3)1(2)1(2)1(2)...n раз...2}
fωω3(n) >{n,n(4)2} = {n,n(3)1(3)1(3)1(3)...n-1 раз...2}
fωω4(n) > {n,n(5)2} = {n,n(4)1(4)1(4)1(4)...n-1 раз...2}
fωωω(n) > {n,n(n)2} = {n,n(n-1)1(n-1)1(n-1)1(n-1)...n-1 раз...2}
Чтобы еще усилить рекурсию можно размещать вхождения внутри разделителя, вот так: {n,n(n)2} = {n,n(1,2)2}. Подобные контрукции называются составным разделителем, их наличие в нотации объясняет весьма усложненный процесс исключений, который так же зарекурсирован внутрь себя, как раз чтобы развертывать составные разделители в обычные. Так, например, в соответствии с его правилами, мы получаем {n,m,2(1,2)2} = {n,n({n,n({n,n(...)2})2})2} - где m-1 вложений. После чего вновь проходим по кругу вышеописанных рекурсий, пока не дойдем до {n,m(2,2)2} = {n,n(1,2)1(1,2)1(1,2)1(1,2)...2} - где m-1 единиц между разделителями. Затем наращиваем рекурсии внутри разделителя по принципу: {n,n(n,2)2} = {n,n(1,3)2} и {n,n(n,n)2} = {n,n(1,1,2)2}, пока не достигнем {n,m(1(2)2)2} = {n,n(n,n,n,n,n,...)2} - где m вхождений внутри = {n,n(1,1,1,...2)2} - где m единиц, что являет собой разделитель вложенный в разделитель. Для того чтобы не запутаться в этом, в правилах вычисления нотации было добавлено понятие "слой разделителя", при этом сам массив называется "базовым слоем". Разворачивать рекурсии необходимо начиная с самого внутреннего слоя, и после того как расширение произошло во всех разделителях этого слоя, переходить к внешнему, таким образом, пока не доберемся до базового слоя, подобный рекурсивный механизм как раз и прописан в процессе исключений (случай B2 и B3). Думаю всем понятно, что это выводит рекурсии на новый уровень. Давайте сразу на примерах посмотрим куда нас это приведет:
fωωω(n) > {n,n(1,2)2} = {n,n(n)2}
fωωω+1(n) > {n,n,2(1,2)2} = {n,n({n,n(...{n,n(n)2}...)2})2} n-1 вложений
fωωω+ω(n) > {n,n,1,2(1,2)2} = {n,n,n(1,2)2}
fωωω+ωω(n) > {n,n(2)2(1,2)2} = {n,n,1,1,1,...n-1 раз...2(1,2)2} = {n,n,n,n,n,...n-1 раз...(1,2)2}
fωωω+ωω2(n) > {n,n(3)2(1,2)2} = {n,n(2)1(2)1(2)1(2)...n-1 раз...2(1,2)2}
fωωω×2(n) > {n,n(1,2)3} = {n,n(n)2(1,2)2}
fωωω+1(n) > {n,n(1,2)1,2} = {n,n(1,2)n}
fωωω+ω(n) > {n,n(1,2)1(2)2} = {n,n(1,2)1,1,1,...n раз...2} = {n,n(1,2)n,n,n,...n раз...}
fωωω+ω2(n) > {n,n(1,2)1(3)2} = {n,n(1,2)1(2)1(2)1(2)...n раз...2}
fωωω×2(n) > {n,n(1,2)1(1,2)2} = {n,n(1,2)1(n)2}
fωωω×3(n) > {n,n(1,2)1(1,2)1(1,2)2} = {n,n(1,2)1(1,2)1(n)2}
fωωω+1(n) > {n,n,(2,2)2} = {n,n(1,2)1(1,2)1(1,2)...n-1 раз...2}
fωωω+1+1(n) > {n,n,2(2,2)2} = {n,{n,...{n,n,(2,2)2}...,(2,2)2},(2,2)2} n-1 вложений
fωωω+1+ωω(n) > {n,n(2)2(2,2)2} = {n,n,1,1,1,...n-1 раз...2(2,2)2} = {n,n,n,n,n,...n-1 раз...(2,2)2}
fωωω+1+ωωω(n) > {n,n(1,2)2(2,2)2} = {n,n(n)2(2,2)2}
fωωω+1×2(n) > {n,n(2,2)3} = {n,n(1,2)1(1,2)1(1,2)...n-1 раз...2(2,2)2}
fωωω+1+1(n) > {n,n(2,2)1,2} = {n,n(2,2)n}
fωωω+1+ω(n) > {n,n(2,2)1(2)2} = {n,n(2,2)1,1,1,...n раз...2} = {n,n(2,2)n,n,n,...n раз...}
fωωω+1+ωω(n) > {n,n(2,2)1(1,2)2} = {n,n(2,2)1(n)2}
fωωω+1×2(n) > {n,n(2,2)1(2,2)2} = {n,n(2,2)1(1,2)1(1,2)1(1,2)...n раз...2}
fωωω+1×3(n) > {n,n(2,2)1(2,2)1(2,2)2} = {n,n(2,2)1(2,2)1(1,2)1(1,2)1(1,2)...n раз...2}
fωωω+2(n) > {n,n,(3,2)2} = {n,n(2,2)1(2,2)1(2,2)...n-1 раз...2}
fωωω×2(n) > {n,n(1,3)2} = {n,n,(n,2)2}
fωωω×2+1(n) > {n,n,2(1,3)2} = {n,n({n,n,(...{n,n,(n,2)2}...,2)2},2)2} n-1 вложений
fωωω×2+ωωω(n) > {n,n(1,2)2(1,3)3} = {n,n(n)2(1,3)2}
fωωω×2×2(n) > {n,n(1,3)3} = {n,n(n,2)2(1,3)2}
fωωω×2+1(n) > {n,n(1,3)1,2} = {n,n(1,3)n}
fωωω×2+1(n) > {n,n(2,3)2} = {n,n(1,3)1(1,3)1(1,3)...n-1 раз...2}
fωωω×2+2(n) > {n,n(3,3)2} = {n,n(2,3)1(2,3)1(2,3)...n-1 раз...2}
fωωω×3(n) > {n,n(1,4)2} = {n,n,(n,3)2}
fωωω2(n) > {n,n(1,1,2)2} = {n,n(n,n)2}
fωωω2+1(n) > {n,n,2(1,1,2)2} = {n,n(n,{n,n(n,...{n,n(n,n)2}...)2})2} n-1 вложений
fωωω2×2(n) > {n,n(1,1,2)3} = {n,n(n,n)2(1,1,2)2}
fωωω2+1(n) > {n,n(1,1,2)1,2} = {n,n(1,1,2)n}
fωωω2+ωω(n) > {n,n(1,1,2)1(1,2)2} = {n,n(1,1,2)1(n)2}
fωωω2×2(n) > {n,n(1,1,2)1(1,1,2)2} = {n,n(1,1,2)1(n,n)2}
fωωω2+1(n) > {n,n(2,1,2)2} = {n,n(1,1,2)1(1,1,2)1(1,1,2)...n-1 раз...2}
fωωω2+2(n) > {n,n(3,1,2)2} = {n,n(2,1,2)1(2,1,2)1(2,1,2)...n-1 раз...2}
fωωω2+ω(n) > {n,n(1,2,2)2} = {n,n(n,1,2)2}
fωωω2+ω+1(n) > {n,n(2,2,2)2} = {n,n(1,2,2)1(1,2,2)1(1,2,2)...n-1 раз...2}
fωωω2+ω×2(n) > {n,n(1,3,2)2} = {n,n(n,2,2)2}
fωωω2×2(n) > {n,n(1,1,3)2} = {n,n(n,n,2)2}
fωωω3(n) > {n,n(1,1,1,2)2} = {n,n(n,n,n)2}
fωωω4(n) > {n,n(1,1,1,1,2)2} = {n,n(n,n,n,n)2} n раз...
fωωωω(n) > {n,n(1(2)2)2} = {n,n(1,1,1,...n раз...2)2} = {n,n(n,n,n,...n раз...)2}
fωωωω+1(n) > {n,n,2(1(2)2)2} = {n,{n,...{n,n(1(2)2)2}...(1(2)2)2}(1(2)2)2} n-1 вложений
fωωωω×2(n) > {n,n(1(2)2)3} = {n,n(1,1,1,...n раз...2)2(1(2)2)2} = {n,n(n,n,n,...n раз...)2(1(2)2)2}
fωωωω+1(n) > {n,n(1(2)2)1(1(2)2)2} = {n,n(1(2)2)1(1,1,1,...n раз...2)2} = {n,n(1(2)2)1(n,n,n,...n раз...)2}
fωωωω×2(n) > {n,n(2(2)2)2} = {n,n(1(2)2)1(1(2)2)1(1(2)2)...n-1 раз...2}
fωωωω+1(n) > {n,n(1,2(2)2)2} = {n,n(n(2)2)2}
fωωωω×2(n) > {n,n(1(2)3)2} = {n,n(1,1,1,...n раз...2(2)2)2} = {n,n(n,n,n,...n раз...(2)2)2}
fωωωω+1(n) > {n,n(1(2)1,2)2} = {n,n(1(2)n)2}
fωωωω×2(n) > {n,n(1(2)1(2)2)2} = {n,n(1(2)1,1,1,...n раз...2)2} = {n,n(1(2)n,n,n,...n раз...)2}
fωωωω2(n) > {n,n(1(3)2)2} = {n,n(1(2)1(2)1(2)...n раз...2)2}
fωωωω3(n) > {n,n(1(4)2)2} = {n,n(1(3)1(3)1(3)...n раз...2)2}
f5ω(n) > {n,n(1(1,2)2)2} = {n,n(1(n)2)2}
f6ω(n) > {n,n(1(1(2)2)2)2} = {n,n(1(1,1,1,...n раз...2)2)2} = {n,n(1(n,n,n,...n раз...)2)2}
f7ω(n) > {n,n(1(1(1,2)2)2)2} = {n,n(1(1(n)2)2)2}
f8ω(n) > {n,n(1(1(1(2)2)2)2)2} = {n,n(1(1(1,1,1,...n раз...2)2)2)2} = {n,n(1(1(n,n,n,...n раз...)2)2)2}
fnω(n) > {n,n(1(1(1...(2)...2)2)2)2} - где (n-2)/2 вложений для четных n; n > 1
fnω(n) > {n,n(1(1(1... (1,2) ...2)2)2)2} - где (n-3)/2 вложений для нечетных n; n > 1
Вот такой головокружительной рекурсии позволяет достичь Расширенная массивная нотация. Особого внимания заслуживает ординал, которым нумеруется функция быстрорастущей иерархии fωω(n) сопоставимая с пределом Расширенной массивной нотации. Тетрация ωω, она же бесконечная степенная башня ωωωω... или ε0 (эпсилон-нуль) - как чаще всего называют этот ординал. Рекурсия уровня fωω(n) соответствует той рекурсии, которая не может быть алгоритмически создана средствами Арифметики первого порядка, на основе тех самых аксиом Пеано (PA), которые мы рассмотрели в начале второй части. Вот мы и достигли таких чисел, на основе которых строилась знаменитая Теорема Гёделя о неполноте, оказавшаяся применимой для любых теорий включающих или выводящих арифметику натуральных чисел. Хочу напомнить, что мы говорим уже не столь а самом числе, сколько о способе получения этого числа. Вспомните миллион из первой части, который я изобразил в натуральном виде как множество точек, но средствами десятичной нотации мы легко могли кратко записать это число, как "1000000". Так вот, числа соизмеримые или бо́льшие чем fωω(n) мы уже не сможем так же кратко записать средствами аксиом Арифметики первого порядка, и сама запись таких чисел будет для нашего восприятия почти соизмерима с его натуральным видом, а как мы оговорились в начале этой части, допускается не более 20 символов. Хочу оговориться, что в данном контексте речь идет только о доказуемо вычислимых числах, то есть таких числах, для которых мы можем запрограммировать алгоритм вычисления отталкиваясь только от аксиом Арифметики Пеано, и этот алгортим гарантировано их вычислит (пусть и физически это, можно сказать, невозможно). Хотя в Арифметике Пеано могут быть весьма кратко определены ещё бо́льшие числа, но увы уже алгоритмически невычислимые, о них мы поговорим намного позже.
Ну а неоднородность бесконечности уровня ωω это максимально-возможная неоднородность, которую можно создать на основе аксиом Арифметики первого порядка или теоретико-доказательственный ординал теории (PTO). Доказательство этого факта было первым успехом в ординальном исчислении, оно было получено в 1936 году немецким математиком Карлом Генценом[162], для этого он использовал введеный им метод исчисления секвенций, который достаточно сложно объяснить без серьезного погружения в математическую логику (далее я приведу более простой способ объяснения того почему ωω является PTO для Арифметики Пеано). Совокупность иррациональных чисел, которые упорядочиваются ординалом ωω называют числами вычислимыми в арифметике Пеано. Множество таких чисел счетное, но оно намного больше множества алгебраических чисел (которое упорядочивается уже ординалом ωω) и помимо собственно подмножества алгебраических чисел оно так же содержит и большое подмножество трансцендентных чисел.
Обратите внимание, что ординал, участвующий в функции быстрорастущей иерархии для создания максимально возможной рекурсии в Арифметике Пеано, равен ординалу создающему максимально возможную неупорядоченность в бесконечности средствами Арифметики Пеано (или PTO теории). Но с подсистемами Арифметики первого порядка такового совпадения не было. Напомню, что:
Арифметика Робинсона (Q) - рекурсия: f1(n) - PTO: ω
Рудиментарно-функциональная арифметика (RFA) - рекурсия: f2(n) - PTO: ω2
Элементарно-функциональная арифметика (EFA) - рекурсия: f3(n) - PTO: ω3
Примитивно-рекурсивная арифметика (PRA) - рекурсия: fω(n) - PTO: ωω
Однако особо внимательные могут заметить взаимосвязь. Действительно, функции быстрорастущей иерархии, в своем определении уже содержат рекурсию (fα+1(n) = fαn(n)), поэтому и возникает такое расхождение на целую степень ωn между ординалом иерархии и теоретико-доказательственным ординалом теории. Наиболее естественным для измерения рекурсий, возможных в рамках аксиоматических систем, будет использование иерархии основанной на ином принципе:
h0(n) = n.
hα+1(n) = hα(n+1).
hα(n) = hα[n](n), где α - предельный ординал,
α[n] - n-ный элемент фундаментальной последовательности ординала α.
Такая иерархия была придумана задолго до быстрорастущей, в 1904 году математиком Годфри Харольдом Харди[163]. Семейство функций соотвественно называются функциями иерархии Харди. И поначалу эта иерархия растет очень медленно, однако начиная с ωn скорость роста уже сопоставима с функциями быстрорастущей иерархии. И далее скорость роста иерархий будет отличаться лишь на одну ступень степенной башни: fk(n) = hωk(n). Тогда все подсистемы Арифметики первого порядка, возможности к рекурсированию которых измерены иерархией Харди, будут соответствовать своему PTO в иерархии. Кроме того иерархия Харди позволит точнее померять скорость рекурсий, которые создаются в рамках этих подсистем.
h0(n) = n
h1(n) = n+1 = f0(n)
h2(n) = n+2 = f0(f0(n))
hω(n) = 2×n = f1(n)
hω+1(n) = 2×(n+1) = f1(f0(n))
hω+2(n) = 2×(n+2) = f1(f0(f0(n)))
hω×2(n) = 4×n = f1(f1(n))
hω×3(n) = 8×n = f1(f1(f1(n)))
hω2(n) = 2n×n = f2(n)
hω2+1(n) = 2n+1×(n+1) = f2(f0(n))
hω2+2(n) = 2n+2×(n+2) = f2(f0(f0(n)))
hω2+ω(n) = 22×n×(2×n) = f2(f1(n))
hω2+ω×2(n) = 24×n×(4×n) = f2(f1(f1(n)))
hω2×2(n) = 22n×n×(2n×n) = f2(f2(n))
hω2×3(n) = 222n×n×(2n×n)×(22n×n×(2n×n)) = f2(f2(f2(n)))
hω3(n) = f3(n) > 2[4]n
hω4(n) = f4(n) > 2[5]n
hωω(n) = fω(n) > n[n+1]n
hωω+1(n) = fω(f0(n)) > n[n+2]n
hωω+ω(n) = fω(f1(n)) > n[2×n]n
hωω+ω2(n) = fω(f2(n)) > n[2n×n]n
hωω×2(n) = fω(fω(n)) > n[n[n+1]n]n
hωω×3(n) = fω(fω(fω(n))) > n[n[n[n+1]n]n]n
hωω+1(n) = fω+1(n)
hωω×2(n) = fω×2(n)
hωω2(n) = fω2(n)
hωω3(n) = fω3(n)
hωωω(n) = fωω(n)
hωωωω(n) = fωωω(n)
h5ω(n) = f4ω(n)
h6ω(n) = f5ω(n)
hωω(n) ≈ fωω(n)
Можно заметить, что как только мы достигаем рекурсии уровня ωω = ωωωω... = ε0, с которой уже не справляется Арифметика первого порядка происходит то, что называют схождением рекурсий. То есть, конечно fωω(n) растет быстрее hωω(n), и соответственно fωω+1(n) будет расти быстрее hωω+1(n). Однако hωω+1(n) растет несравненно быстрее чем fωω(n). Получается, что всегда, начиная с ординала ωω, скорость рекурсий обеих иерархий будет "примерно" одинаковой, а еще это означает, что для всех теорий, более сильных чем Арифметика первого порядка, их PTO (ординал упорядочивающий максимальную алгоритмически достижимую неоднородность бесконечности) будет совпадать с ординалом в функции быстрорастущей иерархии (предел максимально-возможной рекурсии на натуральных числах). Два известных нам способа измерения силы аксиоматических систем, по сути, свелись к одному.
Ординалы, которые являются пределами для тех или иных теорий, обычно являются пределами для множества рекурсивных функций. В сущности, то что PTO теории является пределом для рекурсивной функции, которая использует все возможности аксиом этой теории, лишний раз доказывает правоту Теоремы Гёделя о неполноте. Так например, так называемая Теорема Гудстейна, является аналогом Теоремы Гёделя для Арифметики первого порядка, доказывая ее неполноту и непротиворечивость[164]. Но давайте я начну не с сути Теоремы Гудстейна, а с примера, так будет проще ее понять. Возьмем число, допустим "6", и разложим его так, чтобы оно было представлено в виде степени или башни степеней с основанием два и последним показателем ноль: 6 = 22+21+20 = 2220+220+20. Теперь заменим все двойки на тройки: 3330+330+30 = 31. Теперь вычтем единицу: 31-1 = 30. Снова представим число в виде разложения, но уже в виде степени или башни степеней с основанием три и последним показателем ноль: 30 = 33+31 = 3330+330. Теперь заменяем все тройки на четверки: 4440+440 = 260. Снова вычитаем единицу: 260-1 = 259 и снова раскладываем число, но уже используя основание четыре: 259 = 44+40+40+40 = 4440+40+40+40, заменяем четверки на пятерки и снова вычитаем единицу: 5550+50+50+50-1 = 3217, и так далее. Думаю основной принцип всем понятен. Так вот, согласно Теореме Гудстейна, любое натуральное число может быть разложено по такому приниципу и в конце-концов сведено к нулю[165]. На первый взгляд это утверждение противоречит интуиции, похоже что в результате разложения число будет только увеличивается. Но давайте возьмем число поменьше, например "3", и за пять шагов убедимся, что для этого числа теорема верна:
1) 3 = 220+20 ⇒ 330+30-1 = 3;
2) 3 = 330 ⇒ 440-1 = 3;
3) 3 = 40+40+40 ⇒ 50+50+50-1 = 2;
4) 2 = 50+50 ⇒ 60+60-1 = 1;
5) 1 = 60 ⇒ 70-1 = 0.
Однако не просто будет убедиться, вот так же на примере поэтапного разложения, что и для числа "4" теорема тоже верна, потому что для этого потребуется 3×2402653211-3 шагов, что примерно равно 10121210695. А это уже прецедент для создания быстрорастущей функции, которую так и называют Функцией Гудстейна G(n). Функция определяет сколько шагов требуется для разложения числа n по Теореме Гудстейна. В целом скорость роста этой функции, как вы догадались, оценивается fωω(n), вернее стоит сказать hωω(n), причем ее можно очень точно сопоставить с функциями иерархии Харди, что мы и сделаем ниже. Эти сопоставления имеют очень глубокий смысл. Если вы проследите за сравениями, то поймете как трансфинитные ординалы связаны с рекурсиями над натуральными числами.
Любое натуральное число можно разложить на подобные степенные башни с использованием любого натурального основания, которое будет меньше данного числа, например:
100 = 26+25+22 = 22220+220+22220+20+2220
100 = 34+32+32+30 = 3330+30+330+30+330+30+30
100 = 43+42+42+41 = 440+40+40+440+40+440+40+440
и т.д.
Это называется разложением по супероснованию. Здесь то как раз и кроется взаимосвязь с аксиомами арифметики, в этом процессе проверяется вся мощь аксиомы математической индукции. Проверяется на прочность сам принцип индукции, что любое корректное математическое утверждение об n, верное и для n+1, должно быть верно для всех натуральных чисел. Ну и как следует из Теоремы Гёделя о неполноте и как показывает Теорема Гудстейна принцип математической индукции не может быть проверен в рамках аксиом арифметики первого порядка[164], а только в рамках более сильной теории, имеющей PTO > ωω.
G(0) = G(0) = h0(3)-3 = 0
G(1) = G(1) = h1(3)-3 = 1
G(2) = G(2) = hω(3)-3 = 3
G(3) = G(2+1) = hω+1(3)-3 = 5
G(4) = G(22) = hωω(3)-3
G(5) = G(22+1) = hωω+1(3)-3
G(6) = G(22+2) = hωω+ω(3)-3
G(7) = G(22+2+1) = hωω+ω+1(3)-3
G(8) = G(22+1) = hωω+1(3)-3
G(9) = G(22+1+1) = hωω+1+1(3)-3
G(10) = G(22+1+2) = hωω+1+ω(3)-3
G(11) = G(22+1+2+1) = hωω+1+ω+1(3)-3
G(12) = G(22+1+22) = hωω+1+ωω(3)-3
G(13) = G(22+1+22+1) = hωω+1+ωω+1(3)-3
G(14) = G(22+1+22+2) = hωω+1+ωω+ω(3)-3
G(15) = G(22+1+22+2+1) = hωω+1+ωω+ω+1(3)-3
G(16) = G(222) = hωωω(3)-3
G(32) = G(222+1) = hωωω+1(3)-3
G(64) = G(222+2) = hωωω+ω(3)-3
G(128) = G(222+2+1) = hωωω+ω+1(3)-3
G(256) = G(222+1) = hωωω+1(3)-3
G(512) = G(222+1+1) = hωωω+1+1(3)-3
G(1024) = G(222+1+2) = hωωω+1+ω(3)-3
G(2048) = G(222+1+2+1) = hωωω+1+ω+1(3)-3
G(4096) = G(222+1+22) = hωωω+1+ωω(3)-3
G(8192) = G(222+1+22+1) = hωωω+1+ωω+1(3)-3
G(16384) = G(222+1+22+2) = hωωω+1+ωω+ω(3)-3
G(32768) = G(222+1+22+2+1) = hωωω+1+ωω+ω+1(3)-3
G(65536) = G(2222) = hωωωω(3)-3
G(52) = h5ω(3)-3
G(62) = h6ω(3)-3
G(n2) < hωω(n)-3
Другая теорема, которая так же является аналогом Теоремы о Неполноте для Арифметики первого порядка, называется Теоремой Кирби-Париса[164]. Происходит эта теорема из теории игр. Мы имеем дело с игрой определенного вида, которую называют Гидра. В мифе о Геракле гидра была чудовищем с уникальной способностью, лишившись одной головы она отращивала на ее месте две новых. Понятно, что тактика сражения в виде отсечения голов не позволит победить гидру, и с каждой отрубленной головой она будет становится только сильнее. Давайте изобразим нашу гидру используя скобки: (()()()) - представьте, что это трехголовая гидра, вид сверху. Отрубаем левую голову (()()()) и на ее месте вырастает две новые (()()()()). Как мы выяснили, такая гидра непобедима. Мы можем еще усилить ее непобедимость, дав гидре способность отращивать не две, а три или четыре или h - голов, назовем число h - регенеративной способностью гидры.
В Теореме Кирби-Париса мы сражаемся с гидрой несколько иной природы. Во-первых у этой гидры головы могут расти не только из туловища, но и из других голов, например так: ((())()()). Во-вторых голова отрубленная от туловища больше не вырастает, однако отрубать головы можно только если от них не растут другие головы. Ну и самое главное правило: после отрубания головы, не растущей от туловища, гидра отращивает целые ветки голов, начиная от узла, к которому была прикреплена голова, от которой отрубили голову. Давайте формально запишем правила этой игры:
Голова - a,
Узел, к которому она крепится - b,
Узел, к которому крепится этот узел - с,
и т.д.
Туловище - R.
Регенеративная способность гидры - h.
Если мы отрубаем голову a, то:
1) если голова прикреплена к туловищу (b = R) - ничего не происходит
2) если голова прикреплена к некому узлу, который не является туловищем (b ≠ R) - тогда от узла c создается h копий всего древа, которое осталось на узле c после отрубания головы.
Ниже приведу вам наглядный пример, того что будет происходить с этой гидрой, когда мы начнем с ней сражаться.
рис.55
На первый взгляд кажется, что эта гидра тоже непобедимая как и та, с которой сражался Геракл, и похоже она еще более могущественная. Однако Теорема Кирби-Париса утверждает, что такую гидру всегда можно сразить, вне зависимости от того сколько у нее голов, как они распределены, и вне зависимости от того какой регенеративной способностью обладает гидра. Это утверждение так же как Теорема Гудстейна противоречит интуции, но оно доказывается. Однако доказательство лежит за пределами аксиом Арифметики первого порядка, в рекурсиях столь сильных, что они недоступны нашей интуиции. Для более интуитивного доказательства так же используют трансфитиные ординалами. Каждый уровень, на котором размещается голова, можно пометить ординалом ωk1+ωk2+ωk3+...+ωkn, где n - число голов растущих из этого уровня, ki - ординал головы верхнего уровня, при этом самые верхние головы всегда отмечаются нулевыми ординалами. После отрубания голов гидра не растет вверх, а только вширь, причем получается так, что после каждого отрубания головы, ординал, которым помечается тело, будет уменьшаться, а значит гидру всегда можно убить.
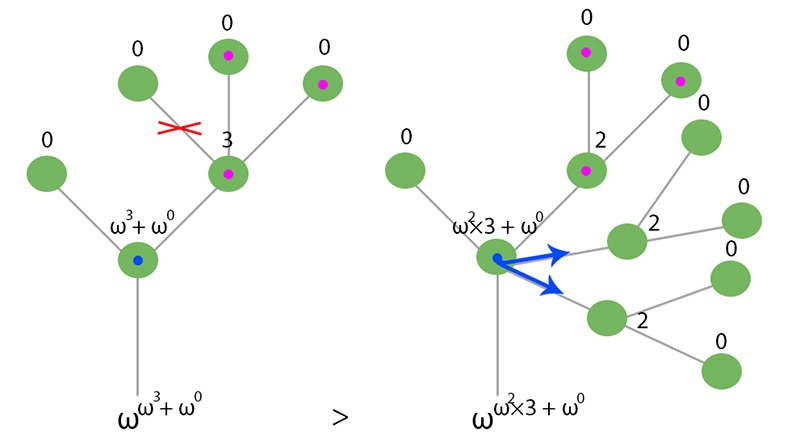
рис.56
Теперь давайте определим быстрорастущую функцию связанную с этой игрой. Итак, имеется гидра в виде линейного графа высотой n (головы растут из голов по одной, тогда n - число голов), функция KPH(n) определеляет сколько понадобится ходов, чтобы победить эту гидру, при условии, что регенеративная способность гидры h = 1, и растет на единицу h = h+1 с каждым ходом. Даже такую гидру, регенерация которой постоянно возрастает, в соотвествии с Теоремой Кирби-Париса, тоже можно уничтожить. Функция KPH(n) растет со скоростью fωω(n) или hωω(n), что "почти" тоже самое. Растущая регенеративная способность это на самом деле связь с математической индукцией (утверждающей что, то что верно для n и для n+1 будет верно для всех натуральных чисел), которая позволяет достигнуть рекурсивных пределов Арифметики первого порядка[164]. Функция KPH(n) может быть точно вычислена в разумных пределах максимум для аргумента n = 3, тогда гидра будет выглядеть так: (((()))). Сражение с такой гидрой займет KPH(3) = 37 ходов, и будет происходить следующим образом:
(((())))
((()()))
((())(())(()))
((())(())()()()())
((())(())()()())
((())(())()())
((())(())())
((())(()))
((())()()()()()()()()())
((())()()()()()()()())
((())()()()()()()())
((())()()()()()())
((())()()()()())
((())()()()())
((())()()())
((())()())
((())())
((()))
(()()()()()()()()()()()()()()())
(()()()()()()()()()()()()()())
(()()()()()()()()()()()()())
(()()()()()()()()()()()())
(()()()()()()()()()()())
(()()()()()()()()()())
(()()()()()()()()())
(()()()()()()()())
(()()()()()()())
(()()()()()())
(()()()()())
(()()()())
(()()())
(()())
(())
()
В целом же значения функции как и в случае с функцией Гудстейна проще выражать через иерархию Харди. Точные соотношения значений, увы, выразить сложно, но приблизительные значения будут следующие:
KPH(0) = 0
KPH(1) = 1
KPH(2) = 3
KPH(3) = 37 > hω×2+4(5) = 36
KPH(4) > hωω×2+4(5)
KPH(5) > hωωω×2+4(5)
KPH(6) > hωωωω×2+4(5)
и т.д.
Теперь, когда мы убедились насколько тесно взаимосвязаны ординалы и рекурсивные функции, давайте с вами подробнее поговорим о том, как именно в ординалах заключены эти рекурсии, которые они в себе несут. Греческая буква ω, символизирующая первый трансфинитный ординал, а так же такие арифметические действия над ним, как сложение, умножение, степень и всевозможные их комбинации, в том числе с использованием десятичных чисел (например, ωωω×3+ωω+5×2+7) - называются ординальной нотацией Кантора. Да, все верно, для записи ординалов нам тоже нужны нотации. При том очень важно, чтобы ординальная нотация была вполне упорядочена - это значит, что средствами нотации потенциально может быть записан любой ординал, вплоть до предельного ординала ее возможостей, и два любых ординала всегда можно сравнить между собой. Хочу отметить разницу между понятиями "все ординалы" и "любой ординал". Понятно, что все ординалы записать невозможно, так как их бесконечно много и даже, если так можно сказать, более чем бесконечно много (0,1,2,3,...n,...ω,ω+1,ω+2,ω+3,...,ω+n,...ω×2,...), но чисто теоретически, пусть даже у вас не будет физической возможности это сделать, любой конкретный ординал, который вы только пожелаете, может быть записан в этой нотации. Однако стоит отметить важное разлчие между ординальными нотациями и нотациями для записи натуральных чисел. У ординальных нотаций всегда есть предел, дальше которого нотация не может записать ординалы конечным способом, это является прямым следствием теоремы Геделя, величина этого предела определяет силу ординальной нотации. Для нотации Кантора пределом является ординал ωω - бесконечная степенная башня из ω, поскольку тетрация не включена в нотацию, то никакой конечной возможности записать этот ординал и все последующие у нее нет. Нотации для натуральных чисел же теоретически могут записать любое натуральное число, дай им только место для записи, будь это хоть натуральный вид, в котором можно нарисовать сколько угодно палочек (хотя, для того чтобы судить о силе нотации, мы тоже можем поставить ограничение, например на количество символов для записи, как мы сделали это в начале этой главы). Способность до своего предела записать любой ординал конечным способом называют нормальной формой ординальной нотации. Нормальная форма ординальной нотации Кантора[112] определяется следующим образом:
Любой ненулевой ординал α < ωω можно запиcать в виде:
α = ωβ1+ωβ2+...+ωβk-1+ωβk, где α > β1 ≥ β2 ≥ ... ≥ βk-1 ≥ βk
На самом деле, из этого правила записи получается что для ординальной нотации Кантора не нужны даже десятичные цифры, нужен только ноль, потому что любое натуральное число можно записать так: n = ω0+ω0+ω0+ω0+... - n-раз, например: 3 = ω0+ω0+ω0. Операция умножения тоже не нужна, поскольку ее можно заменить, либо сложением, либо степенью, например: ωω×ω2 = ωω×ω×ω = ωω+1×ω = ωω+2 = ωω+ω0+ω0. Короче говоря, каждый ординал в Нормальной форме Кантора, по сути, является некой гидрой Кирби-Париса, и чем более живучая получилась гидра, тем бо́льший ординал мы имеем. Подобные преобразования нужны для формальных алгоритмических подсчетов, чтобы можно было легко и просто сравнить два любых ординала по величине. А мы можем продолжать использовать десятичные цифры и умножение, чтобы сохранить привычное интуитивное понимание ординалов. Но все же, если в ординальной нотации для каждого ординала будет работать формальный вычислительный алгоритм, позволяющий сравнить по величине два любых ординала, записанных в нормальной форме, значит такая нотация является вполне упорядоченной, и в ней корректно можно определить фундаментальные последовательности.
Давайте подробнее остановимся на этом понятии, потому что фундаментальные последовательности это очень важный момент в гугологии. Итак, фундаментальная последовательность определяется только для счетного предельного ординала, ей называется строго возрастающая последовательность ординалов, пределом которой он является[166]. Для любого счетного предельного ординала, такая последовательность всегда будет счетно-бесконечной (содержать ℵ0 элементов) и не содержащей трансфинтиных разрывов, это напрямую следует из свойств счетных ординалов, ведь каждый из них может быть неким определенным способом сопоставлен с рядом натуральных чисел. Тут важно понимать, что фундаментальные последовательности это бесконечные множества, которые сами по себе еще не являются ординалами. Ведь, по определению, ординалы это такие множества, которые образованы по приципу включения всех предыдущих, так например: 1 = {0} , 2 = {0,1} , ω = {0,1,2,3,4,...} , ω+1 = {0,1,2,3,4,...ω} , ω×2 = {0,1,2,3,4,...ω,ω+1,ω+2,ω+3,...} и т.д. То есть, не каждое множество является ординалом, а только включающее в себя все предыдущие ординалы. С другой стороны мы можем определить, например, ординал ω2, как предел фундаментальной последовательности {ω,ω×2,ω×3,ω×4, ...}, но при этом сама последовательность это не то множество, которое представляет собой ординал ω2. Потому что ω2 = {0,1,2,3,4,... ω,ω+1,ω+2,ω+3,... ω×2,ω×2+1,ω×2+2,ω×2+3,... ω×3,ω×3+1,ω×3+2,ω×3+3..., . . . }. Более того, любой ординал бо́льший чем ω, будучи множеством, не может быть последовательностью без трансфинтиных разрывов (без троеточий между ординалами, символизирующих бесконечное количество элементов между ними). И ω - это единственный ординал, фундаментальная последовательность которого совпадает с ним самим. Значит, когда мы используем фундаментальную последовательность как множество для получения ординала, их нельзя приравнивать, а в этом случае используется понятие супремум (sup), означающее верхнюю грань множества. Супремум - это либо максимальный элемент множества, если такой есть, либо если его нет, как в случае с бесконечно возрастающей последовательностью, минимальный ординал бо́льший чем каждый член последовательности. И такой ординал должен существовать, потому что это напрямую следует из аксиомы бесконечности, в соответствии с которой, предел некоторой бесконечной последовательности ординалов, тоже является ординалом. Поэтому более корректно следует расписывать ординалы на образующие их фундаментальные последовательности таким образом: ω×2 = sup(ω+1,ω+2,ω+3,...,ω+n,...)n<ω , ω2 = sup(ω×1,ω×2,ω×3,...,ω×n,...)n<ω , ωω = sup(ω1,ω2,ω3,...,ωn,...)n<ω , и держать в голове, что данные предельные ординалы включают в себя не только членов последовательности, но и всевозможные ординалы, которые могут быть между ними и перед ними.
Однако здесь кроется одна проблема, дело в том, что для одного и того же ординала может быть определено несколько разных фундаментальных последовательностей и он будет супремумом для каждой из них. К примеру ω×2 = sup(ω+2,ω+4,ω+6,...,ω+n×2,...)n<ω , ω2 = sup(ω×1+1,ω×2+2,ω×3+3,...,ω×n+n,...)n<ω , для обоих этих последовательностей супремумами будут ординалы ω×2, и ω2 соотвественно. А так же для них можно придумать еще великое множество других последовательностей, и каждая из них тоже может являться фундаментальной. И когда в функциях быстрорастущей иерархии или иерархии Харди, или любой другой рекурсивной иерархии завязанной на трансфинитных ординалах, мы используем ту самую хитрость, меняя ординал на заложенную в нем рекурсию, то мы как раз и задействуем фундаментальные последовательности[166]. А теперь внимание, если для самого ординала этот момент не имеет большого значения, ведь все фундаментальные последовательности что его образуют одинаково бесконечны, то для рекурсий на конечных числах очень важно какую именно фундаментальную последовательность использовать. Потому что в рекурсивных иерархиях мы обычно вместо ординального "и так до бесконечности", используем "и так n-раз". И это самое n зависит от того какой член фундаментальной последовательности там находится. То есть, наша задача, начиная с n-ного номера, n-раз пройтись обратно по рекурсивной цепочке создающей ординал, и от того насколько рекурсивно эффективен будет этот обратный путь зависит размер получаемой рекурсии. Конечно если на этом обратном пути мы учтем каждый ординал и используем его фундаметнальную последовательность так же эффективно, то создаваемая рекурсия на конечных числах будет сильнее.
Для нотации Кантора эффективные фундаментальные последовательности формально записываются следующим образом[166]:
ω[n] = n;
(ωα1+...+ωαk-1+ωαk)[n] = ωα1+...+ωαk-1+ωαk[n] - где α1 ≥ ... ≥ αk-1 ≥ αk;
ωα+1[n] = ωα×n;
ωα[n] = ωα[n] - где α - предельный ординал;
ωω[0] = 0; ωω[n+1] = ω(ωω)[n] = nω.
Немного поясню, что это значит. Запись α[n] = f(n) обозначает, что n-ный элемент ординала α находится по некой формуле f взятой от n. Например: ω[5] = 5; (ω×2)[5] = ω+ω[5] = ω+5; ω2[5] = ω×5; (ω2+ω)[5] = ω2+5; и т.д. Тех кто не понял формальную запись определения фундаментальных нотаций, но внимательно следил за примерами, которые я приводил когда показывал как разворачиваются рекурсии при подстановке трансфинитных ординалов в функции быстрорастущей иерархии, я спешу успокоить, что они и так уже знают, что такое фундаментальные последовательности и как они работают. Ну а если вы не понимаете зачем нужны эти формальные сложности, поскольку вы и так интуитивно понимаете работу рекурсии, то попробуйте написать формальный алогритм для компьютера, который будет рассчитывать эту рекурсию, и вы вскоре поймете, что компьютер не может как вы инутитивно чувствовать ординалы и менять их бесконечность на конечную рекурсивность, поэтому для него нужны строгие формальные определения фундаментальных последовательностей.
Пределом для нотации Кантора является ординал ωω - иногда его называют Малым ординалом Кантора (Small Cantor ordinal), и как мы выяснили, он уже не может быть записан конечным способом с использованием лишь "ω","0" сложения и возведения в степень. Поэтому фундаментальная последовательность для него определена отдельно, и в соответствии с правилами будет: fωω(n) = n-1ω, где fωω(0) = 0 - исключение. Обращаю внимание, что рекурсия: fωω+1(n) = fω↑↑fω↑↑fω↑↑...fω↑↑n(n)...(...)(...)(...) - n раз, где две стрелки в соответствии с нотацией Кнута обозначают тетрацию - уже лежит за пределами возможностей нотации Кантора, но в своей рекурсии использует эту отдельно определенную фундаментальную последовательность, и как вы можете заметить, делает новый рекурсивный скачек.
Чтобы расширить нотацию Кантора вводят понятие эпсилон-нуль: ε0 = ωωωω... = ωω. Это делается, потому что с тетрацией над ординалами cвыше ωω работать уже нельзя, как я объяснял еще во второй части, тетрация не может быть неупорядоченной бесконечностью. Вот вам простой пример: ω+1ω = ω(ωω) = ω(ωωω...) = ωωωω... = ωω. Как же тогда нам продвигаться дальше, спросите вы? Для начала нам нужно понять, что такое неподвижные точки (fixed point) и как их преодолеть. В математике этим термином называют ситуацию когда f(n) = n, то есть функция возвращает сам аргумент, который и был в нее подставлен. Например, для функции натурального квадрата n2 неподвижными точками будут 0 и 1, поскольку 02 = 0 и 12 = 1. Получается, что ε0 - это неподвижная точка для функции ωn, поскольку ωε0 = ω(ωωω...) = ωωωω... = ε0. Функции, на которых есть ординальные неподвижные точки записываются так: α↦f(α), например, стандартное определение гласит, что ε0 - это первая неподвижная точка α↦ωα. В ординальном анализе неподвижные точки всегда совпадают с некими предельными ординалами. Давайте задумаемся, каким другим способом можно получить ε0, потому что, если совсем досконально подойти к выражению ωω, то вообще-то некорректно говорить, что "ε0 = ωω - это степенная башня ωωωω... из бесконечного количества ω", потому что тогда мы получается говорим о кардинале, количественной бесконечности. Если мы хотим получить что-то порядковое, то нам в определении нужно слово "последовательность", а не "количество". Тогда лучше сказать так ε0 = ωω - это предел фундаментальной последовательности {ω,ωω,ωωω,ωωωω, ...}. Получается, что ординальные неподвижные точки, так же как любые другие предельные ординалы, проще и правльнее выразить как пределы для некой фундаментальной последовательности. Тут важно понимать то что я объяснял до этого, что ε0 ≠ {ω,ωω,ωωω,ωωωω,...}, то есть эта последовательность будучи множеством не является сама по себе ε0, и более того это множество вообще не является ординалом. Ну а в свою очередь, ε0, являясь ординалом, содержит в себе все предыдущие ординалы, и ω×2, и ω3, и ωω+1, и т.д., которых нет в последовательности {ω,ωω,ωωω,ωωωω,...}.
И так же как функция натурального квадрата n2 имеет больше одной неподвижной точки (точнее две: 0 и 1), ординальная функция ωn, тоже имеет больше одной неподвижной точки, а точнее бесконечное количество и даже более чем бесконечное, но давайте доберемся хотя бы до второй неподвижной точки. Вначале попробуем увеличивать нашу первую неподвижную точку ε0 самым простым способом: ωωωω...+1 = ε0+1, и о чудо, мы сдвинулись с места: ε0+1 > ωε0, поскольку ωε0 = ω(ωωω...) = ωωωω... = ε0. Дальше поступаем следующим образом: ω(ωωω...+1) = ωε0+1; ωω(ωω...+1) = ωωε0+1; ωωω(ω..+1) = ωωωε0+1 и снова получаем бесконечную последовательность {ε0+1,ωε0+1,ωωε0+1,ωωωε0+1,ωωωωε0+1,...}, так вот ωωω...ε0+1 = ε1 - предел этой последовательности и это же вторая неподвижная точка α↦ωα (потому что ω(ωω...ε0+1) = ωωω...ε0+1), с которой опять непросто сдвинуться, например: ωε1 = ε0ε1 = ε1. Соответственно: ωωω...ε1+1 = ε2 - будет третьей неподвижной точкой α↦ωα и уже ωε2 = ε0ε2 = ε1ε2 = ε2. Как вы, наверное, заметили в формулах с нумерациями неподвижных точек происходит тоже, что и с самими ординалами, их нумеруют начиная с нуля. Я уже объяснял почему такая нумерация более верная, могу только добавить что даже в аксиомах Пеано арифметики первого порядка нуль называют первым натуральным числом, поэтому иногда и происходит такая путаница.
Здесь давайте на секунду остановимся в создании неподвижных точек и отметим ряд важных преобразований, которые легко можно вывести из правил ординальной арифметики, основывающихся на все тех же формулах работы со степенями из алгебры седьмого класса.
ε0×ω = ωωωω...×ω = ω(ωωω...+1) = ωε0+1
ε0×ε0 = ωωωω...×ωωωω... = (ωωωω...)2 = ω(ωωω...×2) = ωε0×2
ε0ω = (ωωωω...)ω = ω(ωωω...×ω) = ωε0×ω = ωωε0+1
ε0ε0 = (ωωωω...)ωωω... = ω(ωωω...×ωωω...) = ωωε0×2
ε0ε0ω = ωωε0×ω = ωωωε0+1
и т.д.
Из этих преобразований выводится интересное следствие: ε0ε0ε0ε0...= ωωω...ε0+1 = ε1. Получается ε1 так же можно определить как бесконечную тетрацию над ε0, то есть ωε0 = ε1. Значит ε1 будет первой неподвижной точкой для функции α↦ε0α и пределом последовательности sup(1ε0,2ε0,3ε0,...,nε0,...)n<ω. Подобные преобразования со степенями можно применять и дальше, так ε1×ω = ωε1+1 и ε1×ε0 = ε0ε1+1 или ε1ω = ωωε1+1 и ε1ε0 = ε0ε0ε1+1. Ну и следовательно: ε1ε1ε1ε1...= ε0ε0ε0...ε1+1 = ωωω...ε1+1 = ε2 - является третьей неподвижной точкой α↦ωα, или второй неподвижной точкой α↦ε0α, или первой неподвижной точкой α↦ε1α. Так же стоит отметить важную деталь, что первая неподвижная точка ординальной функции α↦f(α) обычно обладает интересным свойством, ее можно получить так: α = fω(n), где n - любой ординал меньший α, то есть мы просто бесконечно подставляем функцию саму в себя, например: ε0 = fω(ωn) = sup(n,ωn,ωωn,ωωωn,...)n<ω; ε1 = fω(ε0n) = sup(n,ε0n,ε0ε0n,ε0ε0ε0n,...)n<ω; ε2 = fω(ε1n) = sup(n,ε1n,ε1ε1n,ε1ε1ε1n,...)n<ω и т.д.
Но чтобы не запутаться во всей этой иерархии неподвижных точек обычно принято сводить все рекурсивные операции над этими эпсилонами, бо́льшие чем "×ω", но меньшие чем "↑↑ω", в вид степенной башни из омег подставленных под них, считая номера неподвижных точек именно от операции α↦ωα. Так что в более общем смысле всегда действует правило: εnεnεnεn...= ωωω...εn+1 = εn+1. В дальнейшем вы увидите, что это следствие распространяется на все ординалы являющиеся неподвижными точками α↦ωα, и перечисленные выше свойства по преобразованию степеней для первой неподвижной точки (ε0) так же выполняются для любой неподвижной точки α↦ωα.
α×ω = ωα+1
α×α = ωα×2
αω = ωα×ω = ωωα+1
αα = ω(α×α) = ωωα×2
ααω = ωωα×ω = ωωωα+1
и т.д., где α - любая неподвижная точка α↦ωα
Но пока давайте вернемся к массивной нотации, следующее расширение которой называется Примитивно расширяющаяся массивная нотация. Расширение начинается с введения разделителя следующего порядка, который записывается так "(1.)" (или просто как точка "."), и расширяется следующим образом: {n,m(1.)2} = {n,n(1(1(1(1... , ...2)2)2)2)2} - где m-1 вложений разделителей. Но такое расширение очень слабое, а мы достигли уже такого уровня рекурсий, что для того чтобы добраться от функции быстрорастущей иерархии взятой от первой неподвижной точки α↦ωα - fε0(n) до этой функции взятой хотя бы от второй неподвижной точки α↦ωα - fε1(n) нужны кардинальные рекурсивные преобразования. Как вы наверное заметили, когда добираешься до нового рекурсивного предела, чтобы дальше сделать хотя бы один шажок в направление следующего предела необходимо снова пройти через круговорот рекурсий, что мы уже совершили, только сделать это на совершенно новом уровне. Поэтому такая начальная рекурсия как {n,m,2(1.)2} = {n,n(1(1(1(1... , ...2)2)2)2)2} - где число вложений {n,n(1(1(1(1... , ...2)2)2)2)2} - где число вложений... и так m-1 раз - будет сопоставима лишь с fε0+1(n). Даже пробравшись сквозь первый круг рекурсий, когда мы получим: {n,m(1.)3} = {n,n(1(1(1(1... , ...2)2)2)2)2(1.)2} - где m-1 вложений разделителей - мы достигнем лишь fε0×2(n). Второй круг рекурсий приведет нас к следующему выражению: {n,m(1.)1(1.)2} = {n,n(1.)1(1(1(1(1... , ...2)2)2)2)2} - где m-1 вложений разделителей - но и это всего лишь fε02(n). Продолжать подобные процедуры можно до {n,m(2.)2} = {n,n(1.)1(1.)1(1.)1(1.)...2} - где m единичных вхождений - это будет уже разделитель следующего порядка второго уровня. Но если вам кажется, что вот мы уже и достигли скорости роста сопоставимой с fε1(n), то смею вас разочаровать скорость роста выражений массивной нотации с разделителем "(2.)" оценивается как fε0ω(n).
Затем будем увеличивать уровень разделителей следующего порядка: {n,m(3.)2}, {n,m(4.)2} и так вплоть до {n,m(n.)2} = {n,m(1,2.)2}. Это приведет нас к fε0ωω(n). Разделитель следующего порядка тоже может иметь вхождения и разделители. Так, например, {n,m(1(1.)2.)2} = {n,n(1(1(1(1(1... , ...2)2)2)2)2.)2} - где m-1 вложений разделителей первого порядка. Конечно, а почему бы и нет. Что соответствует, кстати, fε0ε0(n), и вот мы уже можем городить степенные башни из эпсилонов в функциях быстрорастущей иерерахии. Между прочим, чтобы сделать систему единообразной разделители первого порядка можно записывать так: "," - "(1)" - "(1.0)"; "(2)" - "(2.0)"; тогда разделители второго порядка будем записывать так: "." - "(1.)" - "(1.1)"; "(2.)" - "(2.1)"; естественно напрашивается создание разделителя третьего порядка: {n,m(1.2)2} = {n,n(1(1(1(1... , ...2.)2.)2.)2.)2} - где m-1 вложений разделителей второго порядка. И здесь мы наконец-то добрались до fε1(n). Так можно продолжать и далее, создавая разделители все высших и высших порядков, в общем случае схема будет выглядеть так: (1.k) = (1(1(1(1... , ...2.k-1)2.k-1)2.k-1)2.k-1). Собственно разделители каждого следующего порядка будут по скорости роста соотвествовать каждой следующей неподвижной точке α↦ωα подставленной в функцию быстрорастущей иерархии: fεk-1(n) > {n,n(1.k)2} при k > 0. Можно было бы продолжать и дальше, создавая вхождения и разделители уже в самом порядке, а потом сделать порядок порядка, но на этом выражении {n,n(1.n)2} текущее расширение массивной нотации останавливается. Просто вспомните его название: "Примитивно расширяющаяся массивная нотация", то есть такая схема расширения считается примитивной и вводится лишь как вводный курс перед по-настоящему мощными расширениями. Давайте и мы на этом остановимся, ознакомимся с правилами и подробно проанализируем скорость роста выражений. Так же хочу сделать небольшую ремарку по поводу всех последующих сравнений выражений массивной нотации. Поскольку начиная с ε0 скорость роста функций быстрорастущей иерархии и функций иерархии Харди практически сходится, то здесь и далее я буду использовать знак "~~", обозначающий следующее: "α ~~ {n,n...}" = "fα(n) > hα(n) > {n,n,...} > fk(n) > hk(n)", где k<α. Ну а в последующих прямо сейчас сравнениях я буду выражать ординальные операции на неподвижных точках α↦ωα (то есть εn) двумя разными способами: используя степенные башни из них самих, и используя степенные башни из омег подставленных под них, чтобы вы еще раз наглядно проследили за этими преобразованиями, поскольку их правильное понимание будет залогом для понимания дальнейших рекурсий, что мы будем с вами создавать.
Примитивно расширяющаяся масcивная нотация (Primitive expanding array notation)
Определение:
Действительны все определения Extended array notation.
Действителен алгоритм сравнения уровней Extended array notation.
. = (1.) = (1.1) - разделитель следующего порядка, равный
(1(1…(1(1,2)2)…2)2) где b-1 вложений.
“.” - точка (символ ASCII=46) указывает порядок разделителя.
Разделители разных порядков так же могут иметь вхождения,
например
(2.),
(3.),
(1,2.),
(1(1,2)2.),
(1(1.)2.) и т.д.
(1.2) - разделитель еще большего порядка, равный
(1(1…(1(1,2.)2.)…2.)2.) где b-1 вложений.
(1.k) = (1(1…(1(1,2.k-1)2.k-1)…2.k-1)2.k-1)
При сравнении уровня разделители бо́льшего порядка всегда имееют бо́льший уровень.
Правила:
Правило 1: (Правило базы - если в массиве два вхождения)
{a S b} = {a,b} = ab
Правило 2: (Правило хвоста - если последнее вхождение массива или разделителя равно 1)
{# S 1} = {#} или (# S 1) = (#)
Правило 3: (Правило рекурсии - если 2-е и 3-е вхождение не равно 1)
{a,b,c #} = {a,{a,b-1,c #},c-1 #}
Правило 4: (Правило сокращения - если lv(S) < lv(S
+), для массива или разделителя) {# S 1 S
+ #
+} = {# S
+ #
+} или (# S 1 S
+ #
+) = (# B #
+)
“#” и “#
+” - какие-то строки вхождений и разделителей, также могут быть пустыми.
“S” и “S
+” - какие-то разделители.
Процесс:
Циклично и последовательно проверяем выполнение 4-х приведенных выше правил, пока не выполнится первое правило.
Если ни одно из 4-х приведенных выше правил не применяется, то запускается процесс исключений.
Начинаем с 3-ого вхождения:
Случай A: Если вхождение равно 1, тогда переходим к следующему вхождению.
Случай B: Если вхождение не равно 1, тогда смотрим на предыдущий элемент:
Случай B1: Если это запятая “,” тогда:
1) изменяем “1,n” (это вхождение и предыдущую единицу)
на “b,n-1”, где b - итератор.
2) изменяем все предыдущие вхождения в базовом слое на a, где a - база.
3) закончить и перейти к проверке правил.
Случай B2: Если это разделитель вида
“(1.k)” тогда:
1) изменяем
“(1.k) n” на
“Sb 2 (1.k) n-1”,
где b - итератор,
S1 - “,” - запятая, и
Si+1 = (1 Si 2.k-1) при k > 1 или
Si+1 = (1 Si 2) при k = 1.
2) закончить и перейти к проверке правил.
Случай B3: Если это разделитель “S”, не являющийся запятой или разделителем вида
“(1.k)”, тогда:
1) изменяем
“S n” на
“S 2 S n-1”.
2) переходим к первому вхождению в первом из S.
Случай B4: Если это открывающаяся скобка “(” тогда:
1) изменяем разделитель “
(n #)” на строку S
b, где b это итератор,
S1 = “(n-1 #)” и
Si+1 = “Si 1 (n-1 #)”.
2) закончить и перейти к проверке правил.
Первоначальное авторство: Крис Бёрд, 2013 год.
[167]
Последующая модификация: Hypcos, 2015 год.
[168]
приложение 12 (Примитивно расширяющаяся массивная нотация)
ε0 ~~ {n,n(1.)2} = {n,n(1(1(1(1... , ...2)2)2)2)2} n-1 вложений
ε0+1 ~~ {n,n,2(1.)2} = {n,{n,...{n,n(1.)2}...(1.)2}(1.)2} n-1 вложений
ε0+2 ~~ {n,n,3(1.)2} = {n,{n,...{n,n(1.)2}...,2(1.)2},2(1.)2} n-1 вложений
ε0+ω ~~ {n,n,1,2(1.)2} = {n,n,n(1.)2}
ε0+ω+1 ~~ {n,n,2,2(1.)2} = {n,n,{n,n,...{n,n,n(1.)2}...(1.)2}(1.)2} n-1 вложений
ε0+ω×2 ~~ {n,n,1,3(1.)2} = {n,n,n,2(1.)2}
ε0+ω2 ~~ {n,n,1,1,2(1.)2} = {n,n,n,n(1.)2}
ε0+ω2+1 ~~ {n,n,2,1,2(1.)2} = {n,n,n,{n,n,n,...{n,n,n,n,(1.)2}...(1.)2}(1.)2} n-1 вложений
ε0+ω2+ω ~~ {n,n,1,2,2(1.)2} = {n,n,n,1,2(1.)2}
ε0+ω2×2 ~~ {n,n,1,1,3(1.)2} = {n,n,1,n,2(1.)2}
ε0+ω3 ~~ {n,n,1,1,1,2(1.)2} = {n,n,n,n,n(1.)2}
ε0+ωω ~~ {n,n(2)2(1.)2} = {n,n,1,1,1,...n-1 раз...2(1.)2}
ε0+ωω+1 ~~ {n,n,2(2)2(1.)2} = {n,{n,...{n,n(2)2(1.)2}...(2)2(1.)2}(2)2(1.)2} n-1 вложений
ε0+ωω+ω ~~ {n,n,1,2(2)2(1.)2} = {n,n,n(2)2(1.)2}
ε0+ωω+ω2 ~~ {n,n,1,1,2(2)2(1.)2} = {n,n,n,n(2)2(1.)2}
ε0+ωω×2 ~~ {n,n(2)3(1.)2} = {n,n,1,1,1,...n-1 раз...2(2)2(1.)2}
ε0+ωω+1 ~~ {n,n(2)1,2(1.)2} = {n,n(2)n(1.)2}
ε0+ωω+1+1 ~~ {n,n,2(2)1,2(1.)2} = {n,n(2){n,n(2)...{n,n(2)n(1.)2}...(1.)2}(1.)2} n-1 вложений
ε0+ωω+1+ωω ~~ {n,n(2)2,2(1.)2} = {n,n,1,1,1,...n-1 раз...2(2)1,2(1.)2}
ε0+ωω+1×2 ~~ {n,n(2)1,3(1.)2} = {n,n(2)n,2(1.)2}
ε0+ωω+2 ~~ {n,n(2)1,1,2(1.)2} = {n,n(2)n,n(1.)2}
ε0+ωω×2 ~~ {n,n(2)1(2)2(1.)2} = {n,n(2)1,1,1,...n раз...2(1.)2}
ε0+ωω×3 ~~ {n,n(2)1(2)1(2)2(1.)2} = {n,n(2)1(2)1,1,1,...n раз...2(1.)2}
ε0+ωω2 ~~ {n,n(3)2(1.)2} = {n,n(2)1(2)1(2)1(2)...n-1 раз...(1.)2}
ε0+ωω3 ~~ {n,n(4)2(1.)2} = {n,n(3)1(3)1(3)1(3)...n-1 раз...(1.)2}
ε0+ωωω ~~ {n,n(1,2)2(1.)2} = {n,n(n)2(1.)2}
ε0+ωωω+1 ~~ {n,n(2,2)2(1.)2} = {n,n(1,2)1(1,2)1(1,2)1(1,2)...n-1 раз...2(1.)2}
ε0+ωωω×2 ~~ {n,n(1,3)2(1.)2} = {n,n(n,2)2(1.)2}
ε0+ωωω2 ~~ {n,n(1,1,2)2(1.)2} = {n,n(n,n)2(1.)2}
ε0+ωωω3 ~~ {n,n(1,1,1,2)2(1.)2} = {n,n(n,n,n)2(1.)2}
ε0+ωωωω ~~ {n,n(1(2)2)2(1.)2} = {n,n(1,1,1,...n раз...2)2(1.)2}
ε0+ωωωω+1 ~~ {n,n(2(2)2)2(1.)2} = {n,n(1(2)2)1(1(2)2)1(1(2)2)1(1(2)2)...n раз...2(1.)2}
ε0+ωωωω+ω ~~ {n,n(1,2(2)2)2(1.)2} = {n,n(n(2)2)2(1.)2}
ε0+ωωωω×2 ~~ {n,n(1(2)3)2(1.)2} = {n,n(1,1,1,...n раз...2(2)2)2(1.)2}
ε0+ωωωω+1 ~~ {n,n(1(2)1,2)2(1.)2} = {n,n(1(2)n)2(1.)2}
ε0+ωωωω×2 ~~ {n,n(1(2)1(2)2)2(1.)2} = {n,n(1(2)1,1,1,...n раз...2)2(1.)2}
ε0+ωωωω2 ~~ {n,n(1(3)2)2(1.)2} = {n,n(1(2)1(2)1(2)1(2)...n раз...2)2(1.)2}
ε0+ωωωωω ~~ {n,n(1(1,2)2)2(1.)2} = {n,n(1(n)2)2(1.)2}
ε0+6ω ~~ {n,n(1(1(2)2)2)2(1.)2} = {n,n(1(1(1,1,1,...n раз...2)2)2)2(1.)2}
ε0+7ω ~~ {n,n(1(1(1,2)2)2)2(1.)2} = {n,n(1(1(n)2)2)2(1.)2}
ε0+8ω ~~ {n,n(1(1(1(2)2)2)2)2(1.)2} = {n,n(1(1(1,1,1,...n раз...2)2)2)2(1.)2}
ε0×2 ~~ {n,n(1.)3} = {n,n(1(1(1(1... , ...2)2)2)2)2(1.)2} n-1 вложений
ε0×2+1 ~~ {n,n,2(1.)3} = {n,{n,...{n,n(1.)3}...(1.)3}(1.)3} n-1 вложений
ε0×2+ω ~~ {n,n,1,2(1.)3} = {n,n,n(1.)3}
ε0×2+ωω ~~ {n,n(2)2(1.)3} = {n,n,1,1,1,...n-1 раз...2(1.)3}
ε0×2+ωωω ~~ {n,n(1,2)2(1.)3} = {n,n(n)2(1.)3}
ε0×2+ωωωω ~~ {n,n(1(2)2)2(1.)3} = {n,n(1,1,1,...n раз...2)2(1.)3}
ε0×2+ωωωωω ~~ {n,n(1(1,2)2)2(1.)3} = {n,n(1(n)2)2(1.)3}
ε0×3 ~~ {n,n(1.)4} = {n,n(1(1(1(1... , ...2)2)2)2)2(1.)3} n-1 вложений
ε0×4 ~~ {n,n(1.)5} = {n,n(1(1(1(1... , ...2)2)2)2)2(1.)4} n-1 вложений
ε0×ω = ωε0+1 ~~ {n,n(1.)1,2} = {n,n(1.)n}
ε0×(ω+1) = ωε0+1+ε0 ~~ {n,n(1.)2,2} = {n,n(1(1(1(1... , ...2)2)2)2)2(1.)1,2} n-1 вложений
ε0×(ω×2) = ωε0+1×2 ~~ {n,n(1.)1,3} = {n,n(1.)n,2}
ε0×ω2 = ωε0+2 ~~ {n,n(1.)1,1,2} = {n,n(1.)n,n}
ε0×ω3 = ωε0+3 ~~ {n,n(1.)1,1,1,2} = {n,n(1.)n,n,n}
ε0×ωω = ωε0+ω ~~ {n,n(1.)1(2)2} = {n,n(1.)1,1,1,...n раз...2}
ε0×(ωω+1) = ωε0+ω+ε0 ~~ {n,n(1.)2(2)2} = {n,n(1(1(1(1... , ...2)2)2)2)1(2)2} n-1 вложений
ε0×(ωω+ω) = ωε0+ω+ωε0+1 ~~ {n,n(1.)1,2(2)2} = {n,n(1.)n(2)2}
ε0×(ωω×2) = ωε0+ω×2 ~~ {n,n(1.)1(2)3} = {n,n(1.)1,1,1,...n раз...2(2)2}
ε0×ωω+1 = ωε0+ω+1 ~~ {n,n(1.)1(2)1,2} = {n,n(1.)1(2)n}
ε0×ωω×2 = ωε0+ω×2 ~~ {n,n(1.)1(2)1(2)2} = {n,n(1.)1(2)1,1,1,...n раз...2}
ε0×ωω2 = ωε0+ω2 ~~ {n,n(1.)1(3)2} = {n,n(1.)1(2)1(2)1(2)...n раз...2}
ε0×ωωω = ωε0+ωω ~~ {n,n(1.)1(1,2)2} - {n,n(1.)1(n)2}
ε0×ωωωω = ωε0+ωωω ~~ {n,n(1.)1(1(2)2)2} = {n,n(1.)1(1,1,1,...n раз...2)2}
ε0×ωωωωω = ωε0+ωωωω ~~ {n,n(1.)1(1(1,2)2)2} = {n,n(1.)1(1(n)2)2}
ε02 = ωε0×2 ~~ {n,n(1.)1(1.)2} = {n,n(1.)1(1(1(1(1... , ...2)2)2)2)2} n-1 вложений
ε02×2 = ωε0×2×2 ~~ {n,n(1.)1(1.)3} = {n,n(1.)1(1(1(1(1... , ...2)2)2)2)1(1.)2} n-1 вложений
ε02×ω = ωε0×2+1 ~~ {n,n(1.)1(1.)1,2} = {n,n(1.)1(1.)n}
ε02×ωω = ωε0×2+ω ~~ {n,n(1.)1(1.)1(2)2} = {n,n(1.)1(1.)1,1,1,...n раз...2}
ε02×ωωω = ωε0×2+ωω ~~ {n,n(1.)1(1.)1(1,2)2} = {n,n(1.)1(1.)1(n)2}
ε02×ωωωω = ωε0×2+ωωω ~~ {n,n(1.)1(1.)1(1(2)2)2} = {n,n(1.)1(1.)1(1,1,1,...n раз...2)2}
ε03 = ωε0×3 ~~ {n,n(1.)1(1.)1(1.)2} = {n,n(1.)1(1.)1(1(1(1(1... , ...2)2)2)2)2} n-1 вложений
ε0ω = ωωε0+1 ~~ {n,n(2.)2} = {n,n(1.)1(1.)1(1.)1(1.)...n-1 раз...2}
ε0ω+1 = ωωε0+1+1 ~~ {n,n,2(2.)2} = {n,{n,...{n,n(2.)2}...(2.)2}(2.)2} n-1 вложений
ε0ω+ω = ωωε0+1+ω ~~ {n,n,1,2(2.)2} = {n,n,n(2.)2}
ε0ω+ωω = ωωε0+1+ωω ~~ {n,n(2)2(2.)2} = {n,n,1,1,1,...n-1 раз...2(2.)2}
ε0ω+ε0 = ωωε0+1+ε0 ~~ {n,n(1.)2(2.)2} = {n,n(1(1(1(1... , ...2)2)2)2)2(2.)2} n-1 вложений
ε0ω+ε0×2 = ωωε0+1+ε0×2 ~~ {n,n(1.)3(2.)2} = {n,n(1(1(1(1... , ...2)2)2)2)2(1.)2(2.)2} n-1 вложений
ε0ω+ε0×ω = ωωε0+1+ωε0+1 ~~ {n,n(1.)1,2(2.)2} = {n,n(1.)n(2.)2}
ε0ω+ε0×ωω = ωωε0+1+ωε0+ω ~~ {n,n(1.)1(2)2(2.)2} = {n,n(1.)1,1,1,...n раз...2(2.)2}
ε0ω+ε02 = ωωε0+1+ωε0×2 ~~ {n,n(1.)1(1.)2(2.)2} = {n,n(1.)1(1(1(1(1... , ...2)2)2)2)2(2.)2} n-1 вложений
ε0ω×2 = ωωε0+1×2 ~~ {n,n(2.)3} = {n,n(1.)1(1.)1(1.)1(1.)...n-1 раз...(2.)2}
ε0ω×ω = ωωε0+1+1 ~~ {n,n(2.)1,2} = {n,n(2.)n}
ε0ω×ωω = ωωε0+1+ω ~~ {n,n(2.)1(2)2} = {n,n(2.)1,1,1,...n раз...2}
ε0ω+1 = ωωε0+1+ε0 ~~ {n,n(2.)1(1.)2} = {n,n(2.)1(1(1(1(1... , ...2)2)2)2)2} n-1 вложений
ε0ω+1×ω = ωωε0+1+ε0+1 ~~ {n,n(2.)1(1.)1,2} = {n,n(2.)1(1.)n}
ε0ω+2 = ωωε0+1+ε0+ε0 ~~ {n,n(2.)1(1.)1(1.)2} = {n,n(2.)1(1.)1(1(1(1(1... , ...2)2)2)2)2} n-1 вложений
ε0ω×2 = ωωε0+1×2 ~~ {n,n(2.)1(2.)2} = {n,n(2.)1(1.)1(1.)1(1.)...n раз...2}
ε0ω×3 = ωωε0+1×3 ~~ {n,n(2.)1(2.)1(2.)2} = {n,n(2.)1(2.)1(1.)1(1.)1(1.)...n раз...2}
ε0ω2 = ωωε0+2 ~~ {n,n(3.)2} = {n,n(2.)1(2.)1(2.)1(2.)...n-1 раз...2}
ε0ωω = ωωε0+ω ~~ {n,n(1,2.)2} = {n,n(n.)2}
ε0ωω+1 = ωωε0+ω+1 ~~ {n,n(2,2.)2} = {n,n(1,2.)1(1,2.)1(1,2.)1(1,2.)...n-1 раз...2}
ε0ωω×2 = ωωε0+ω×2 ~~ {n,n(1,3.)2} = {n,n(n,2.)2}
ε0ωω2 = ωωε0+ω2 ~~ {n,n(1,1,2.)2} = {n,n(n,n.)2}
ε0ωω2+1 = ωωε0+ω2+1 ~~ {n,n(2,1,2.)2} = {n,n(1,1,2.)1(1,1,2.)1(1,1,2.)1(1,1,2.)...n-1 раз...2}
ε0ωω2+ω = ωωε0+ω2+ω ~~ {n,n(1,2,2.)2} = {n,n(n,1,2.)2}
ε0ωω2×2 = ωωε0+ω2×2 ~~ {n,n(1,1,3.)2} = {n,n(n,n,2.)2}
ε0ωω3 = ωωε0+ω3 ~~ {n,n(1,1,1,2.)2} = {n,n(n,n,n.)2}
ε0ωωω = ωωε0+ωω ~~ {n,n(1(2)2.)2} = {n,n(1,1,1,...n раз...2.)2}
ε0ωωω+1 = ωωε0+ωω+1 ~~ {n,n(2(2)2.)2} = {n,n(1(2)2.)1(1(2)2.)1(1(2)2.)1(1(2)2.)...n-1 раз...2}
ε0ωωω+ω = ωωε0+ωω+ω ~~ {n,n(1,2(2)2.)2} = {n,n(n(2)2.)2}
ε0ωωω+ω2 = ωωε0+ωω+ω2 ~~ {n,n(1,1,2(2)2.)2} = {n,n(n,n(2)2.)2}
ε0ωωω×2 = ωωε0+ωω×2 ~~ {n,n(1(2)3.)2} = {n,n(1,1,1,...n раз...2(2)2.)2}
ε0ωωω+1 = ωωε0+ωω+1 ~~ {n,n(1(2)1,2.)2} = {n,n(1(2)n.)2}
ε0ωωω+1+1 = ωωε0+ωω+1+1 ~~ {n,n(2(2)1,2.)2} = {n,n(1(2)1,2.)1(1(2)1,2.)1(1(2)1,2.)1(1(2)1,2.)...n-1 раз...2}
ε0ωωω+1+ωω = ωωε0+ωω+1+ωω ~~ {n,n(2(2)2,2.)2} = {n,n(1,1,1,...n раз...2(2)1,2.)2}
ε0ωωω+1×2 = ωωε0+ωω+1×2 ~~ {n,n(1(2)1,3.)2} = {n,n(2(2)n,2.)2}
ε0ωωω+2 = ωωε0+ωω+2 ~~ {n,n(1(2)1,1,2.)2} = {n,n(2(2)n,n.)2}
ε0ωωω×2 = ωωε0+ωω×2 ~~ {n,n(1(2)1(2)2.)2} = {n,n(1(2)1,1,1,...n раз...2.)2}
ε0ωωω×3 = ωωε0+ωω×3 ~~ {n,n(1(2)1(2)1(2)2.)2} = {n,n(1(2)1(2)1,1,1,...n раз...2.)2}
ε0ωωω2 = ωωε0+ωω2 ~~ {n,n(1(3)2.)2} = {n,n(1(2)1(2)1(2)1(2)...n раз...2.)2}
ε0ωωω3 = ωωε0+ωω3 ~~ {n,n(1(4)2.)2} = {n,n(1(3)1(3)1(3)1(3)...n раз...2.)2}
ε0ωωωω = ωωε0+ωωω ~~ {n,n(1(1,2)2.)2} = {n,n(1(n)2.)2}
ε0ωωωω+1 = ωωε0+ωωω+1 ~~ {n,n(1(2,2)2.)2} = {n,n(1(1,2)1(1,2)1(1,2)1(1,2)...n раз...2.)2}
ε0ωωωω×2 = ωωε0+ωωω×2 ~~ {n,n(1(1,3)2.)2} = {n,n(1(n,2)2.)2}
ε0ωωωω2 = ωωε0+ωωω2 ~~ {n,n(1(1,1,2)2.)2} = {n,n(1(n,n)2.)2}
ε0ωωωω3 = ωωε0+ωωω3 ~~ {n,n(1(1,1,1,2)2.)2} = {n,n(1(n,n,n)2.)2}
ε0ωωωωω = ωωε0+ωωωω ~~ {n,n(1(1(2)2)2.)2} = {n,n(1(1,1,1,...n раз...2)2.)2}
ε06ω = ωωε0+5ω ~~ {n,n(1(1(1,2)2)2.)2} = {n,n(1(1(n)2)2.)2}
ε07ω = ωωε0+7ω ~~ {n,n(1(1(1(2)2)2)2.)2} = n,n(1(1(1,1,1,...n раз...2)2)2.)2}
ε0ε0 = ωωε0×2 ~~ {n,n(1(1.)2.)2} = {n,n(1(1(1(1(1... , ...2)2)2)2)2.)2} n-1 вложений
ε0ε0+1 = ωωε0×2+1 ~~ {n,n,2(1(1.)2.)2} = {n,{n,...{n,n(1(1.)2.)2}...(1(1.)2.)2}(1(1.)2.)2} n-1 вложений
ε0ε0+ε0 = ωωε0×2+ε0 ~~ {n,n(1.)2(1(1.)2.)2} = {n,n(1(1(1(1... , ...2)2)2)2)2(1(1.)2.)2} n-1 вложений
ε0ε0+ε0ω = ωωε0×2+ωωε0+1 ~~ {n,n(2.)2(1(1.)2.)2} = {n,n(1.)1(1.)1(1.)1(1.)...n-1 раз...2(1(1.)2.)2}
ε0ε0×2 = ωωε0×2×2 ~~ {n,n(1(1.)2.)3} = {n,n(1(1(1(1(1... , ...2)2)2)2)2.)2(1(1.)2.)2} n-1 вложений
ε0ε0×ω = ωωε0×2+1 ~~ {n,n(1(1.)2.)1,2} = {n,n(1(1.)2.)n}
ε0ε0+1 = ωωε0×2+ε0 ~~ {n,n(1(1.)2.)1(1.)2} = {n,n(1(1.)2.)1,1,1,...n раз...2}
ε0ε0+ω = ωωε0×2+ωε0+1 ~~ {n,n(1(1.)2.)1(2.)2} = {n,n(1(1.)2.)1(1.)1(1.)1(1.)1(1.)...n раз...2}
ε0ε0×2 = ωωε0×2×2 ~~ {n,n(1(1.)2.)1(1(1.)2.)2} = {n,n(1(1.)2.)1(1(1(1(1(1... , ...2)2)2)2)2.)2} n-1 вложений
ε0ε0×3 = ωωε0×2×3 ~~ {n,n(1(1.)2.)1(1(1.)2.)1(1(1.)2.)2} = {n,n(1(1.)2.)1(1(1.)2.)1(1(1(1(1... , ...2)2)2)2.)2} n-1 вложений
ε0ε0×ω = ωωε0×2+1 ~~ {n,n(2(1.)2.)2} = {n,n(1(1.)2.)1(1(1.)2.)1(1(1.)2.)...n-1 раз...2}
ε0ε0×ωω = ωωε0×2+ω ~~ {n,n(1,2(1.)2.)2} = {n,n(n(1.)2.)2}
ε0ε0×ωωω = ωωε0×2+ωω ~~ {n,n(1(2)2(1.)2.)2} = {n,n(1,1,1,...n раз...2(1.)2.)2}
ε0ε02 = ωωε0×3 ~~ {n,n(1(1.)3.)2} = {n,n(1(1(1(1(1... , ...2)2)2)2)2(1.)2.)2} n-1 вложений
ε0ε03 = ωωε0×4 ~~ {n,n(1(1.)4.)2} = {n,n(1(1(1(1(1... , ...2)2)2)2)2(1.)3.)2} n-1 вложений
ε0ε0ω = ωωωε0+1 ~~ {n,n(1(1.)1,2.)2} = {n,n(1(1.)n.)2}
ε0ε0ω+1 = ωωωε0+1+ε0 ~~ {n,n(1(1.)2,2.)2} = {n,n(1(1(1(1(1... , ...2)2)2)2)2(1.)1,2.)2} n-1 вложений
ε0ε0ω×2 = ωωωε0+1×2 ~~ {n,n(1(1.)1,3.)2} = {n,n(1(1.)n,2.)2}
ε0ε0ω2 = ωωωε0+2 ~~ {n,n(1(1.)1,1,2.)2} = {n,n(1(1.)n,n.)2}
ε0ε0ωω = ωωωε0+ω ~~ {n,n(1(1.)1(2)2.)2} = {n,n(1(1.)1,1,1,...n раз...2.)2}
ε0ε0ωω+1 = ωωωε0+ω+ε0 ~~ {n,n(1(1.)2(2)2.)2} = {n,n(1(1(1(1(1... , ...2)2)2)2)2(1.)1(2)2.)2} n-1 вложений
ε0ε0ωω×2 = ωωωε0+ω×2 ~~ {n,n(1(1.)1(2)3.)2} = {n,n(1(1.)1,1,1,...n раз...2(2)2.)2}
ε0ε0ωω+1 = ωωωε0+ω+1 ~~ {n,n(1(1.)1(2)1,2.)2} = {n,n(1(1.)1(2)n.)2}
ε0ε0ωω×2 = ωωωε0+ω×2 ~~ {n,n(1(1.)1(2)1(2)2.)2} = {n,n(1(1.)1(2)1,1,1,...n раз...2.)2}
ε0ε0ωω2 = ωωωε0+ω2 ~~ {n,n(1(1.)1(3)2.)2} = {n,n(1(1.)1(2)1(2)1(2)1(2)...n раз...2.)2}
ε0ε0ωωω = ωωωε0+ωω ~~ {n,n(1(1.)1(1,2)2.)2} = {n,n(1(1.)1(n)2.)2}
ε0ε0ε0 = ωωωε0×2 ~~ {n,n(1(1.)1(1.)2.)2} = {n,n(1(1.)1(1(1(1(1... , ...2)2)2)2)2.)2} n-1 вложений
ε0ε0ε0×2 = ωωωε0×2×2 ~~ {n,n(1(1.)1(1.)3.)2} = {n,n(1(1.)1(1(1(1(1... , ...2)2)2)2)2(1.)2.)2} n-1 вложений
ε0ε0ε0×ω = ωωωε0×2+1 ~~ {n,n(1(1.)1(1.)1,2.)2} = {n,n(1(1.)1(1.)n.)2}
ε0ε0ε0×ωω = ωωωε0×2+ω ~~ {n,n(1(1.)1(1.)1(2)2.)2} = {n,n(1(1.)1(1.)1,1,1,...n раз...2.)2}
ε0ε0ε0×ωωω = ωωωε0×2+ωω ~~ {n,n(1(1.)1(1.)1(1,2)2.)2} = {n,n(1(1.)1(1.)1(n)2.)2}
ε0ε0ε02 = ωωωε0×3 ~~ {n,n(1(1.)1(1.)1(1.)2.)2} = {n,n(1(1.)1(1.)1(1(1(1(1... , ...2)2)2)2)2.)2} n-1 вложений
ε0ε0ε0ω = ωωωωε0+1 ~~ {n,n(1(2.)2.)2} = {n,n(1(1.)1(1.)1(1.)1(1.)...n раз...2.)2}
ε0ε0ε0ω+1 = ωωωωε0+1+ε0 ~~ {n,n(1(1.)2(2.)2.)2} = {n,n(1(1(1(1(1... , ...2)2)2)2)2(2.)2.)2} n-1 вложений
ε0ε0ε0ω+2 = ωωωωε0+1+ε0×2 ~~ {n,n(1(1.)3(2.)2.)2} = {n,n(1(1(1(1(1... , ...2)2)2)2)2(1.)2(2.)2.)2} n-1 вложений
ε0ε0ε0ω+ω = ωωωωε0+1+ωε0+1 ~~ {n,n(1(1.)1,2(2.)2.)2} = {n,n(1(1.)n(2.)2.)2}
ε0ε0ε0ω+ε0 = ωωωωε0+1+ωε0×2 ~~ {n,n(1(1.)1(1.)2(2.)2.)2} = {n,n(1(1.)1(1(1(1(1... , ...2)2)2)2)2(2.)2.)2} n-1 вложений
ε0ε0ε0ω×2 = ωωωωε0+1×2 ~~ {n,n(1(2.)3.)2} = {n,n(1(1.)1(1.)1(1.)1(1.)...n раз...2(2.)2.)2}
ε0ε0ε0ω×ω = ωωωωε0+1+1 ~~ {n,n(1(2.)1,2.)2} = {n,n(1(2.)n.)2}
ε0ε0ε0ω+1 = ωωωωε0+1+ε0 ~~ {n,n(1(2.)1(1.)2.)2} = {n,n(1(2.)1(1(1(1(1... , ...2)2)2)2)2.)2} n-1 вложений
ε0ε0ε0ω+1×2 = ωωωωε0+1+ε0×2 ~~ {n,n(1(2.)1(1.)3.)2} = {n,n(1(2.)1(1(1(1(1... , ...2)2)2)2)2(1.)2.)2} n-1 вложений
ε0ε0ε0ω+1×ω = ωωωωε0+1+ε0+1 ~~ {n,n(1(2.)1(1.)1,2.)2} = {n,n(1(2.)1(1.)n.)2}
ε0ε0ε0ω+2 = ωωωωε0+1+ε0×2 ~~ {n,n(1(2.)1(1.)1(1.)2.)2} = {n,n(1(2.)1(1.)1(1(1(1(1... , ...2)2)2)2)2.)2} n-1 вложений
ε0ε0ε0ω×2 = ωωωωε0+1×2 ~~ {n,n(1(2.)1(2.)2.)2} = {n,n(1(2.)1(1.)1(1.)1(1.)1(1.)...n раз...2.)2}
ε0ε0ε0ω2 = ωωωωε0+2 ~~ {n,n(1(3.)2.)2} = {n,n(1(2.)1(2.)1(2.)1(2.)...n раз...2.)2}
ε0ε0ε0ω3 = ωωωωε0+3 ~~ {n,n(1(4.)2.)2} = {n,n(1(3.)1(3.)1(3.)1(3.)...n раз...2.)2}
ε0ε0ε0ωω = ωωωωε0+ω ~~ {n,n(1(1,2.)2.)2} = {n,n(1(n.)2.)2}
ε0ε0ε0ωωω = ωωωωε0+ωω ~~ {n,n(1(1(2)2.)2.)2} = {n,n(1(1,1,1,...n раз...2.)2.)2}
ε0ε0ε0ε0 = ωωωωε0×2 ~~ {n,n(1(1(1.)2.)2.)2} = {n,n(1(1(1(1(1(1... , ...2)2)2)2)2.)2.)2} n-1 вложений
ε0ε0ε0ε0×ω = ωωωωε0×2+1 ~~ {n,n(2(1(1.)2.)2.)2} = {n,n(1(1(1.)2.)2.)1(1(1(1.)2.)2.)1(1(1(1.)2.)2.)...n-1 раз...2}
ε0ε0ε0ε0+1 = ωωωωε0×2+ε0 ~~ {n,n(1(1.)2(1(1.)2.)2.)2} = {n,n(1(1(1(1(1... , ...2)2)2)2)2(1(1.)2.)2.)2} n-1 вложений
ε0ε0ε0ε0+ω = ωωωωε0×2+ωε0+1 ~~ {n,n(1(1.)1,2(1(1.)2.)2.)2} = {n,n(1(1.)n(1(1.)2.)2.)2}
ε0ε0ε0ε0+ε0 = ωωωωε0×2+ωε0×2 ~~ {n,n(1(1.)1(1.)2(1(1.)2.)2.)2} = {n,n(1(1.)1(1(1(1(1... , ...2)2)2)2)2(1(1.)2.)2.)2} n-1 вложений
ε0ε0ε0ε0+ε0ω = ωωωωε0×2+ωωε0+1 ~~ {n,n(1(2.)2(1(1.)2.)2.)2} = {n,n(1(1.)1(1.)1(1.)1(1.)...2(1(1.)2.)2.)2}
ε0ε0ε0ε0×2 = ωωωωε0×2×2 ~~ {n,n(1(1(1.)2.)3.)2} = {n,n(1(1(1(1(1(1... , ...2)2)2)2)2.)2(1(1.)2.)2.)2} n-1 вложений
ε0ε0ε0ε0×ω = ωωωωε0×2+1 ~~ {n,n(1(1(1.)2.)1,2.)2} = {n,n(1(1(1.)2.)n.)2}
ε0ε0ε0ε0+1 = ωωωωε0×2+ε0 ~~ {n,n(1(1(1.)2.)1(1.)2.)2} = {n,n(1(1(1.)2.)1(1(1(1(1... , ...2)2)2)2)2.)2} n-1 вложений
ε0ε0ε0ε0×2 = ωωωωε0×2×2 ~~ {n,n(1(1(1.)2.)1(1(1.)2.)2.)2} = {n,n(1(1(1.)2.)1(1(1(1(1(1... , ...2)2)2)2)2.)2.)2} n-1 вложений
ε0ε0ε0ε0×ω = ωωωωε0×2+1 ~~ {n,n(1(2(1.)2.)2.)2} = {n,n(1(1(1.)2.)1(1(1.)2.)1(1(1.)2.)...n раз...2.)2}
ε0ε0ε0ε0×ωω = ωωωωε0×2+ω ~~ {n,n(1(1,2(1.)2.)2.)2} = {n,n(1(n(1.)2.)2.)2}
ε0ε0ε0ε02 = ωωωωε0×3 ~~ {n,n(1(1(1.)3.)2.)2} = {n,n(1(1(1(1(1(1... , ...2)2)2)2)2(1.)2.)2.)2} n-1 вложений
ε0ε0ε0ε0ω = ωωωωωε0+1 ~~ {n,n(1(1(1.)1,2.)2.)2} = {n,n(1(1(1.)n.)2.)2}
ε0ε0ε0ε0ε0 = ωωωωωε0×2 ~~ {n,n(1(1(1.)1(1.)2.)2.)2} = {n,n(1(1(1.)1(1(1(1(1... , ...2)2)2)2)2.)2.)2} n-1 вложений
ε0ε0ε0ε0ε0ω = ωωωωωωε0+1 ~~ {n,n(1(1(2.)2.)2.)2} = {n,n(1(1(1.)1(1.)1(1.)1(1.)...n раз...2.)2.)2}
nε0 ~~ {n,n(1(1(1(1...(1.)...2.)2.)2.)2} - где n/2 вложений для четных n; n > 1
nε0 ~~ {n,n(1(1(1(1...(1.)1(1.)...2.)2.)2.)2} - где (n-1)/2 вложений для нечетных n; n > 1
ε1 = ε0ε0ε0ε0... = ωωωω...ε0+1 ~~ {n,n(1.2)2} = {n,n(1(1(1(1... , ...2.)2.)2.)2.)2} n-1 вложений
ε1+1 ~~ {n,n,2(1.2)2} = {n,{n,...{n,n(1.2)2}...(1.2)2}(1.2)2} n-1 вложений
ε1+ω ~~ {n,n,1,2(1.2)2} = {n,n,n(1.2)2}
ε1+ωω ~~ {n,n(2)2(1.2)2} = {n,n,1,1,1,...n-1 раз...2(1.2)2}
ε1+ε0 ~~ {n,n(1.)2(1.2)2} = {n,n(1(1(1(1... , ...2)2)2)2)2(1.2)2} n-1 вложений
ε1×2 ~~ {n,n(1.2)3} = {n,n,1(1(1(1(1... , ...2.)2.)2.)2.)2(1.2)2} n-1 вложений
ε1×ω = ωε1+1 ~~ {n,n(1.2)1,2} = {n,n(1.2)n}
ε1ω = ωωε1+1 ~~ {n,n(2.2)2} = {n,n(1.2)1(1.2)1(1.2)1(1.2)(1.2)...n-1 раз...2}
ε1ωω = ωωε1+ω ~~ {n,n(1,2.2)2} = {n,n(n.2)2}
ε1ε0 = ωωε1+ε0 ~~ {n,n(1(1.)2.2)2} = {n,n(1(1(1(1(1... , ...2)2)2)2)2.2)2} n-1 вложений
ε1ε1 = ωωε1×2 ~~ {n,n(1(1.2)2.2)2} = {n,n(1(1(1(1(1... , ...2.)2.)2.)2.)2.2)2} n-1 вложений
ε1ε12 = ωωε1×3 ~~ {n,n(1(1.2)3.2)2} = {n,n(1(1(1(1(1... , ...2.)2.)2.)2.)2(1.2)2.2)2} n-1 вложений
ε1ε1ω = ωωωε1+1 ~~ {n,n(1(1.2)1,2.2)2} = {n,n(1(1.2)n.2)2}
ε1ε1ω+1 = ωωωε1+1+ε1 ~~ {n,n(1(1.2)2,2.2)2} = {n,n(1(1(1(1(1... , ...2.)2.)2.)2.)2(1.2)1,2.2)2} n-1 вложений
ε1ε1ω×2 = ωωωε1+1×2 ~~ {n,n(1(1.2)1,3.2)2} = {n,n(1(1.2)n,2.2)2}
ε1ε1ω2 = ωωωε1+2 ~~ {n,n(1(1.2)1,1,2.2)2} = {n,n(1(1.2)n,n.2)2}
ε1ε1ωω = ωωωε1+ω ~~ {n,n(1(1.2)1(2)2.2)2} = {n,n(1(1.2)1,1,1,...n раз...2.2)2}
ε1ε1ε0 = ωωωε1+ε0 ~~ {n,n(1(1.2)1(1.)2.2)2} = {n,n(1(1.2)1(1(1(1(1... , ...2)2)2)2)2.2)2} n-1 вложений
ε1ε1ε0ω = ωωωε1+ωε0+1 ~~ {n,n(1(1.2)1(2.)2.2)2} = {n,n(1(1.2)1(1.)1(1.)1(1.)...n раз...2.2)2}
ε1ε1ε1 = ωωωε1×2 ~~ {n,n(1(1.2)1(1.2)2.2)2} = {n,n(1(1.2)1(1(1(1(1... , ...2.)2.)2.)2.)2.2)2} n-1 вложений
ε1ε1ε1ω = ωωωωε1+1 ~~ {n,n(1(2.2)2.2)2} = {n,n(1(1.2)1(1.2)1(1.2)...n раз...2.2)2}
ε1ε1ε1ω×2 = ωωωωε1+1×2 ~~ {n,n(1(2.2)3.2)2} = {n,n(1(1.2)1(1.2)1(1.2)...n раз...2(2.2)2.2)2}
ε1ε1ε1ω×ω = ωωωωε1+1+1 ~~ {n,n(1(2.2)1,2.2)2} = {n,n(1(2.2)n.2)2}
ε1ε1ε1ω+1 = ωωωωε1+1+ε1 ~~ {n,n(1(2.2)1(1.2)2.2)2} = {n,n(1(2.2)1(1(1(1(1... , ...2.)2.)2.)2.)2.2)2} n-1 вложений
ε1ε1ε1ω×2 = ωωωωε1+1×2 ~~ {n,n(1(2.2)1(2.2)2.2)2} = {n,n(1(2.2)1(1.2)1(1.2)1(1.2)...n раз...2.2)2}
ε1ε1ε1ω2 = ωωωωε1+2 ~~ {n,n(1(3.2)2.2)2} = {n,n(1(2.2)1(2.2)1(2.2)1(2.2)...n раз...2.2)2}
ε1ε1ε1ωω = ωωωωε1+ω ~~ {n,n(1(1,2.2)2.)2} = {n,n(1(n.2)2.2)2}
ε1ε1ε1ε1 = ωωωωε1×2 ~~ {n,n(1(1(1.2)2.2)2.2)2} = {n,n(1(1(1(1(1(1... , ...2.)2.)2.)2.)2.2)2.2)2} n-1 вложений
ε1ε1ε1ε1ω = ωωωωωε1+1 ~~ {n,n(1(1(1.2)1,2.2)2.2)2} = {n,n(1(1(1.2)n.2)2.2)2}
ε1ε1ε1ε1ε1 = ωωωωωε1×2 ~~ {n,n(1(1(1.2)1(1.2)2.2)2.2)2} = {n,n(1(1(1.2)1(1(1(1(1... , ...2.)2.)2.)2.)2.2)2.2)2} n-1 вложений
ε1ε1ε1ε1ε1ω = ωωωωωωε1+1 ~~ {n,n(1(1(2.2)2.2)2.2)2} = {n,n(1(1(1.2)1(1.2)1(1.2)...n раз...2.2)2.2)2}
nε1 ~~ {n,n(1(1(1...(1.2)...2.2)2.2)2.2)2} - где n/2 вложений для четных n; n > 1
nε1 ~~ {n,n(1(1(1...(1.2)1(1.2)...2.2)2.2)2.2)2} - где (n-1)/2 вложений для нечетных n; n > 1
ε2 = ε1ε1ε1ε1... = ωωωω...ε1+1 ~~ {n,n(1.3)2} = {n,n(1(1(1... , ...2.2)2.2)2.2)2} n-1 вложений
ε2×ω = ωε2+1 ~~ {n,n(1.3)1,2} = {n,n(1.3)n}
ε2ω = ωωε2+1 ~~ {n,n(2.3)2} = {n,n(1.3)1(1.3)1(1.3)1(1.3)1(1.3)...n раз...2}
ε2ε2 = ωωε2×2 ~~ {n,n(1(1.3)2.3)2} = {n,n(1(1(1(1... , ...2.2)2.2)2.2)2.3)2} n-1 вложений
ε2ε2ω = ωωωε2+1 ~~ {n,n(1(1.3)1,2.3)2} = {n,n(1(1.3)n.3)2}
ε2ε2ε2 = ωωωε2×2 ~~ {n,n(1(1.3)1(1.3)2.3)2} = {n,n(1(1.3)1(1(1(1... , ...2.2)2.2)2.2)2.3)2} n-1 вложений
ε2ε2ε2ω = ωωωωε2+1 ~~ {n,n(1(2.3)2.3)2} = {n,n(1(1.3)1(1.3)1(1.3)1(1.3)...n раз...2.3)2}
ε2ε2ε2ε2 = ωωωωε2×2 ~~ {n,n(1(1(1.3)2.3)2.3)2} = {n,n(1(1(1(1(1... , ...2.2)2.2)2.2)2.3)2.3)2} n-1 вложений
ε2ε2ε2ε2ω = ωωωωωε2+1 ~~ {n,n(1(1(1.3)1,2.3)2.3)2} = {n,n(1(1(1.3)n.3)2.3)2}
ε2ε2ε2ε2ε2 = ωωωωωε2×2 ~~ {n,n(1(1(1.3)1(1.3)2.3)2.3)2} = {n,n(1(1(1.3)1(1(1(1... , ...2.2)2.2)2.2)2.3)2.3)2}
ε2ε2ε2ε2ε2ω = ωωωωωωε2+1 ~~ {n,n(1(1(2.3)2.3)2.3)2} = {n,n(1(1(1.3)1(1.3)1(1.3)1(1.3)...n раз...2.3)2.3)2}
nε2 ~~ {n,n(1(1(1...(1.3)...2.3)2.3)2.3)2} - где n/2 вложений для четных n; n > 1
nε2 ~~ {n,n(1(1(1...(1.3)1(1.3)...2.3)2.3)2.3)2} - где (n-1)/2 вложений для нечетных n; n > 1
ε3 = ε2ε2ε2ε2... = ωωωω...ε2+1 ~~ {n,n(1.4)2} = {n,n(1(1(1(1... , ...2.3)2.3)2.3)2.3)2} n-1 вложений
ε4 = ε3ε3ε3ε3... = ωωωω...ε3+1 ~~ {n,n(1.5)2} = {n,n(1(1(1(1... , ...2.4)2.4)2.4)2.4)2} n-1 вложений
εω ~~ {n,n(1.n)2}
А мы можем продолжить изучать Расширенную ординальную нотацию Кантора. Ординал εω - это первый предел неподвижных точек α↦ωα, то есть εω = sup(ε0,ε1,ε2,...,εn,...)n<ω. Но при этом сам по себе данный ординал не является первой неподвижной точкой ни для какой операции, но для функции α↦ωα его можно считать неподвижной точкой под номером ω, так как ωεω = εω (в принципе, для любой функции α↦εnα он тоже будет неподвижной точкой под номером ω, так как (εn<ω)εω = εω). Такое совпадение пределов с номерами функциональных особенностей бывает далеко не всегда, и в дальнейших главах мы еще многократно столкнемся с подобными несовпаденями. Но пока все в порядке, и εω+1 будет неподвижной точкой под номером ω+1 для функции α↦ωα, так же она является первой неподвижной точкой для операции α↦εωα, потому что εω+1 = sup(1εω,2εω,3εω,...,nεω,...)n<ω. В целом этот принцип проецируется на любой ординал εn, который будет неподвижной точкой под номером n для функции α↦ωα.
Так что для того, чтобы радикально продвинуться за пределы εω, просто необходимо подставлять все бо́льшие трансфинитные ординалы в индексы эпсилон, обозначающие неподвижные точки α↦ωα, действуя таким образом, мы очень быстро достигнем εε0 - что можно считать неподвижной точкой под номером ε0 для функции α↦ωα или неподвижной точкой №(первая неподвижная точка функции α↦ωα) функции α↦ωα. Затем создадим εεε0 - неподвижную точку под номером εε0 для функции α↦ωα или неподвижную точку №(неподвижная точка №(первая неподвижная точка функции α↦ωα) функции α↦ωα) функции α↦ωα. Да уж, полные названия неподвижных точек становятся все вложеннее и вложеннее. Но тем не менее, у нас вырисовывается новая последовательность {ε0,εε0,εεε0,εεεε0,...}, для которой можно создать новый предел εεεε... - бесконечно нисходящую лестницу из эпсилон.
Это будет первая неподвижная точка α↦εα, иначе ее принято записывать так ζ0 и называть дзета-нуль, а иногда Ординалом Кантора (Cantor ordinal), не путать с ε0 - Малым ординалом Кантора (Small Cantor ordinal). Если мы попытаемся дать ей название отталкиваясь только от функции α↦ωα, то у нас получится бесконечная рекурсия именования, что-то вроде ζ0 - это неподвижная точка №(неподвижная точка №(неподвижная точка №(неподвижная точка №( ... ) функции α↦ωα) функции α↦ωα) функции α↦ωα) функции α↦ωα. Ну или как-то так: ζ0 - это первая неподвижная точка фунции β↦(неподвижная точка №β функции α↦ωα). То есть это уже как бы дважды неподвижная точка для функции α↦ωα или первая 2-неподвижная точка α↦ωα. Но вернемся к тому факту, что для α↦εα это первая неподвижная точка, и раз уже εζ0 = ζ0 = εεεε..., поскольку ε(εεε...) = εεεε..., то для того чтобы двигаться дальше необходимо заходить на новый виток рекурсий. Поскольку ζ0 остается неподвижной точкой для α↦ωα, то следовательно она обладает свойством ωα+1 = α×ω, но а поскольку она еще и неподвижная точка для α↦εα, то у неё появляется еще одно инересное свойство ωα = εα+1, которое будет выполнятся для всех неподвижных точек α↦εα или 2-неподвижных точек α↦ωα, называйте их как хотите. Применим оба свойства к ζ0, чтобы продвинуться к ζ1. Итак для начала: ζ0×ω = ωζ0+1, ζ02 = ωζ0×2, ζ0ω = ωωζ0+1, ζ0ζ0 = ωωζ0×2, ζ0ζ0ω = ωωωζ0+1, ζ0ζ0ζ0 = ωωωζ0×2. Затем: εζ0+1 = ζ0ζ0ζ0ζ0...= ωωω...ζ0+1 и εεζ0+1 = εζ0ζ0ζ0ζ0.... Соответственно ζ1 будет второй неподвижной точкой α↦εα, то есть εζ1 = ζ1, и будет обозначать ζ1 = εεε...ζ0+1.
Аналогичным образом, обозначая номера неподвижных точек α↦εα ординалами, и вкладывая эти обозначения друг в друга, мы в итоге доберемся до ζζζζ..., что будет первой неподвижной точкой α↦ζα, и называется Большим ординалом Кантора (Large Cantor ordinal), для лаконичной записи которого так же имеется греческая буква: η0 (эта-нуль). Если мы так же попробуем именовать его используя только функцию α↦ωα, то у нас получится что-то вроде: η0 - это первая неподвижная точка фунции γ↦(неподвижная точка №γ фунции β↦(неподвижная точка №β функции α↦ωα)). Как видите названия отсылающие нас к исходной ординальной функции, от которой мы начали делать эти построения становятся все сложнее и сложнее. Ну судя по названию, получается, что η0 - это уже трижды неподвижная точка фунции α↦ωα или первая 3-неподвижная точка α↦ωα. Тогда по отношению к фунции α↦εα она будет первой 2-неподвижной точкой. Значит для функции α↦ζα ее можно считать первой 1-неподвижной точкой. Чувствуете как у нас создается иерархия неподвижных точек на каком-то новом уровне.
Добраться до η1 - второй неподвижной точки α↦ζα будет еще сложнее, чем это было ранее, так: εη0+1 = η0η0η0η0... = ωωω...η0+1 , затем: ζη0+1 = εεε...η0+1 и наконец: η1 = ζζζ...η0+1. Конструкции с Большим ординалом Кантора можно продолжать до ηηηη... и для обозначения неподвижных точек α↦ηα нам понадобится другая греческая буква. Но так никаких букв не наберешься.
Однако мы то уже знаем, что вместо букв можно использовать нумерацию, и более того такая нумерацию уже ведется, ведь получается что ординал, который будет первой неподвижной точкой для α↦ηα так же будет четырежды неподвижной точкой α↦ωα или первой 4-неподвижной точкой α↦ωα. Поэтому я предлагаю ввести заглавную букву эпсилон, и добавить ей еще один индекс сзади, так чтобы он обозначал n-неподвижность неподвижной точки α↦ωα, тогда мы получим следующую систему обозначений: 0Ɛn = ωn; 1Ɛn = εn; 2Ɛn = ζn; 3Ɛn = ηn и так далее. Как видно (за исключение случая 0Ɛn), индекс спереди продолжает обозначать номера этих n-неподвижных точек α↦ωα. Тогда ηηηη... = 4Ɛ0, и мы можем продолжать рекурсии дальше: 5Ɛ0 = 4Ɛ4Ɛ4Ɛ4Ɛ...; 6Ɛ0 = 5Ɛ5Ɛ5Ɛ5Ɛ...; ну или в более общем смысле n+1Ɛ0 = nƐnƐnƐnƐ.... Дальше идет ωƐ0, а за ним следует очень важный переход между ωƐ0 и ω+1Ɛ0. Но прежде давайте подумаем, что такое ωƐ0 по отношениюк α↦ωα. Получается, что ωƐ0 это первая ω-неподвижная точка α↦ωα и она же предел n-неподвижных точек α↦ωα, потому что является пределом последовательности {0Ɛ0, 1Ɛ0, 2Ɛ0, 3Ɛ0, ...}. Тут по-прежнему предел совпадает с особенностью ординальной нумерации, но все же стоит помнить, что нет такой функции на n-неподвижных точках α↦ωα, для которой ωƐ0 стал бы первой неподвижной точкой, потому что ωƐ0 для всех функций α↦nƐα будет являться ω-неподвижной точкой.
И пусть из особенностей наименования мы понимаем, что ωƐ1 - это вторая ω-неподвижная точка α↦ωα, но данное определение, ничего не говорит нам о том, как она достигается. Поэтому в данном случае подойдет другое определение ωƐ1 - это второй предел n-неподвижных точек α↦ωα. Ну а достичь его можно следующим способом, выстроив такую бесконечную последовательность: {0Ɛ(ωƐ0)+1 = ω(ωƐ0)+1 = (ωƐ0)×ω, 1Ɛ(ωƐ0)+1 = ε(ωƐ0)+1 = ω(ωƐ0), 2Ɛ(ωƐ0)+1 = ζ(ωƐ0)+1, 3Ɛ(ωƐ0)+1 = η(ωƐ0)+1, ...} - пределом этой последовательности и будет ординал ωƐ1, а вовсе не ωƐωƐ0+1, как могло показаться на первый взгляд, второй ординал будет намного больше. Чтобы лучше понимать почему так получается, давайте дадим имена используемым в образующей последовательности ординалам. Так же как εζ0+1 - можно назвать первой неподвижной точкой α↦ωα после первой 2-неподвижной точки α↦ωα, мы можем назвать 1Ɛ(ωƐ0)+1 - первой неподвижной точкой α↦ωα после первой ω-неподвижной точки α↦ωα. Далее так же как ζη0+1 - можно назвать первой 2-неподвижной точкой α↦ωα после первой 3-неподвижной точки α↦ωα, мы можем назвать 2Ɛ(ωƐ0)+1 - первой 2-неподвижной точкой α↦ωα после первой ω-неподвижной точки α↦ωα. И так далее, в итоге мы получаем последовательность из n-неподвижных точек α↦ωα после первой ω-неподвижной точки α↦ωα, пределом которой и будет ωƐ1 - второй предел n-неподвижных точек α↦ωα, он же вторая ω-неподвижная точка α↦ωα. Правильно будет записать так ωƐ1 = sup(nƐ(ωƐ0)+1|n<ω), это краткая запись для: sup(0Ɛ(ωƐ0)+1, 1Ɛ(ωƐ0)+1, 2Ɛ(ωƐ0)+1, 3Ɛ(ωƐ0)+1, ... , nƐ(ωƐ0)+1, ...)n<ω. А в свою очередь, ωƐ(ωƐ0)+1 - это предел n-неподвижных точек α↦ωα под номером (ωƐ0)+1, он же ω-неподвижная точка α↦ωα под номером (ωƐ0)+1, что явно больше. Может показаться странным, что sup(nƐωƐ0+1|n<ω) < ωƐωƐ0+1, ведь мы знаем, что предел последовательности натуральных чисел: sup(n|n<ω) = ω. Однако мы не всегда можем просто взять и подставить ω на место n в выражении когда речь идет о пределе. В случае, если мы накручиваем меньшие рекурсии на бо́льших рекурсиях, мы иногда сталкиваемся с нотациоными особенностями записи функции, которая задействует все возможности для записи промежуточных ординалов, и может получиться что sup(f(n)|n<ω) ≠ f(ω). Поэтому прежде всего надо обращаться к определениям ординала.
С подобными странностями ординальной арифметики мы еще столкнемся. Ну а ω+1Ɛ0, в свою очередь, будет пределом другой последовательности: {ωƐω, ωƐωƐω, ωƐωƐωƐω, ωƐωƐωƐωƐω, ...}, и, как вы наверное заметили, именно в промежутке между ωƐ1 и ω+1Ɛ0 как раз и отыщется ωƐωƐ0+1. Называться ω+1Ɛ0 будет первая (ω+1)-неподвижная точка α↦ωα. Дальше, в принципе, все должно быть понятно, нам просто надо снова наращивать трансфинитные ординалы, но уже в правом индексе, обозначающем n-неподвижность неподвижных точек α↦ωα. В общем, если хотите пропустить все промежуточные этапы, то сразу переходим к ...Ɛ0Ɛ0Ɛ0Ɛ0Ɛ0 или, как мы уже умеем правильно определять, это будет первая неподвижная точка α↦αƐ0, а еще ее называют Ординалом Фефермана-Шутте (Feferman–Schütte ordinal) и записывают так: Г0 (гамма-нуль)[169]. По отношению к α↦ωα это будет первая неподвижная точка на n↦(n-неподвижности неподвижных точек α↦ωα) или ее можно назвать первая гипер-неподвижная точка. Но рекурсиям как всегда не бывает конца и мы можем определить вторую, третью, n-ную, трансфинитно-ординальную неподвижные точки α↦αƐ0, но пока остановимся на этом ординале, и еще раз оглянемся на проделанные рекурсии.
Сперва давайте еще раз перечислим определения неподвижных точек по отношению к α↦ωα, чтобы они лучше уложились у вас в голове, если после прочитанного вы все еще сумбурно понимаете эту иерархию, так же параллельно будем использовать расширенную нами нотацию Кантора, которая и занимается учетом этих неподвижных точек (хотя стоит признаться, это всего лишь прообраз другой общепринятой нотации, с которой мы тоже познакомимся в дальнейшем). Для краткости я буду записывать "неподвижная точка функции α↦ωα" вот таким образом: "НТ".
ε0 = ωωωω... = 1Ɛ0 = 1-ая НТ
ε1 = ε0ε0ε0ε0...= ωωω...ε0+1 = 1Ɛ1 = 2-ая НТ
ε2 = ε1ε1ε1ε1...= ωωω...ε1+1= 1Ɛ2 = 3-ья НТ
εω = 1Ɛω = ω-ая НТ
εω+1 = εωεωεωεω...= ωωω...εω+1 = 1Ɛω+1 = (ω+1)-ая НТ
εε0 = εωωωω... = 1Ɛ1Ɛ0 = (1-ая НТ)-ая НТ
εεε0 = 1Ɛ1Ɛ1Ɛ0 = ((1-ая НТ)-ая НТ)-ая НТ
εεεε0 = 1Ɛ1Ɛ1Ɛ1Ɛ0 = (((1-ая НТ)-ая НТ)-ая НТ)-ая НТ
ζ0 = εεεε... = 2Ɛ0 = 1Ɛ1Ɛ1Ɛ1Ɛ... = 1-ая 2-НТ
εζ0+1 = ζ0ζ0ζ0ζ0... = ωωω...ζ0+1= 1Ɛ2Ɛ0+1 = 1-ая НТ после 1-ой 2-НТ
εζ0+2 = εζ0+1εζ0+1εζ0+1εζ0+1... = ωωω...εζ0+1+1= 1Ɛ2Ɛ0+2 = 2-ая НТ после 1-ой 2-НТ
εζ0+ε0 = 1Ɛ2Ɛ0+1Ɛ0 = (1-ая НТ)-ая НТ после 1-ой 2-НТ
εζ0+ε1 = 1Ɛ2Ɛ0+1Ɛ1 = (2-ая НТ)-ая НТ после 1-ой 2-НТ
εζ0+εε0 = 1Ɛ2Ɛ0+1Ɛ1Ɛ0 = ((1-ая НТ)-ая НТ)-ая НТ после 1-ой 2-НТ
εζ0+ζ0 = εζ0×2 = 1Ɛ2Ɛ0×2 = (1-ая 2-НТ)-ая НТ после 1-ой 2-НТ
εζ0+ζ0×2 = εζ0×3 = 1Ɛ2Ɛ0×3 = ((1-ая 2-НТ)×2)-ая НТ после 1-ой 2-НТ
εζ0×ω = 1Ɛ2Ɛ0×ω = ((1-ая 2-НТ)×ω)-ая НТ после 1-ой 2-НТ
εεζ0+1 = εζ0ζ0ζ0ζ0...= 1Ɛ1Ɛ2Ɛ0+1 = (1-ая НТ после 1-ой 2-НТ)-ая НТ после 1-ой 2-НТ
εεεζ0+1 = 1Ɛ1Ɛ1Ɛ2Ɛ0+1 = ((1-ая НТ после 1-ой 2-НТ)-ая НТ после 1-ой 2-НТ)-ая НТ после 1-ой 2-НТ
ζ1 = εεε...ζ0+1= 2Ɛ1 = 2-ая 2-НТ
ζ2 = εεε...ζ1+1= 2Ɛ2 = 3-ья 2-НТ
ζω = 2Ɛω = ω-ая 2-НТ
ζε0 = 2Ɛ1Ɛ0 = (1-ая НТ)-ая 2-НТ
ζζ0 = 2Ɛ2Ɛ0 = (1-ая 2-НТ)-ая 2-НТ
ζζζ0= 2Ɛ2Ɛ2Ɛ0 = ((1-ая 2-НТ)-ая 2-НТ)-ая 2-НТ
η0 = ζζζζ... = 3Ɛ0 = 1-ая 3-НТ
εη0+1 = η0η0η0η0... = ωωω...η0+1= 1Ɛ3Ɛ0+1 = 1-ая НТ после 1-ой 3-НТ
εη0+2 = εη0+1εη0+1εη0+1εη0+1... = ωωω...εη0+1= 1Ɛ3Ɛ0+2 = 2-ая НТ после 1-ой 3-НТ
εη0+ε0 = 1Ɛ3Ɛ0+1Ɛ0 = (1-ая НТ)-ая НТ после 1-ой 3-НТ
εη0+η0 = εη0×2 = 1Ɛ3Ɛ0×2 = (1-ая 3-НТ)-ая НТ после 1-ой 3-НТ
εεη0+1 = εη0η0η0η0...= 1Ɛ1Ɛ3Ɛ0+1 = (1-ая НТ после 1-ой 3-НТ)-ая НТ после 1-ой 3-НТ
εεεη0+1 = 1Ɛ1Ɛ1Ɛ3Ɛ0+1 = ((1-ая НТ после 1-ой 3-НТ)-ая НТ после 1-ой 3-НТ)-ая НТ после 1-ой 3-НТ
ζη0+1 = εεε...η0+1= 2Ɛ3Ɛ0+1 = 1-ая 2-НТ после 1-ой 3-НТ
εζη0+1+1 = ζη0+1ζη0+1ζη0+1ζη0+1...= ωωω...ζη0+1+1= 1Ɛ2Ɛ3Ɛ0+1+1 = 1-ая НТ после 1-ой 2-НТ после 1-ой 3-НТ
ζη0+2 = εεε...ζη0+1+1= 2Ɛ3Ɛ0+2 = 2-ая 2-НТ после 1-ой 3-НТ
ζη0+η0 = 2Ɛ3Ɛ0×2 = (1-ая 3-НТ)-ая 2-НТ после 1-ой 3-НТ
ζεη0+1 = ζη0η0η0η0...= 2Ɛ1Ɛ3Ɛ0+1 = (1-ая НТ после 1-ой 3-НТ)-ая 2-НТ после 1-ой 3-НТ
ζζη0+1 = ζζζ...ζη0+1 = 2Ɛ2Ɛ3Ɛ0+1 = (1-ая 2-НТ после 1-ой 3-НТ)-ая 2-НТ после 1-ой 3-НТ
ζζζη0+1 = 2Ɛ2Ɛ2Ɛ3Ɛ0+1 = ((1-ая 2-НТ после 1-ой 3-НТ)-ая 2-НТ после 1-ой 3-НТ)-ая 2-НТ после 1-ой 3-НТ
η1 = ζζζ...η0+1= 3Ɛ1 = 2-ая 3-НТ
η2 = ζζζ...η1+1 = 3Ɛ2 = 3-ья 3-НТ
ηω = 3Ɛω = ω-ая 3-НТ
ηε0 = 3Ɛ1Ɛ0 = (1-ая НТ)-ая 3-НТ
ηζ0 = 3Ɛ2Ɛ0 = (1-ая 2-НТ)-ая 3-НТ
ηη0 = 3Ɛ3Ɛ0 = (1-ая 3-НТ)-ая 3-НТ
ηηη0 = 3Ɛ3Ɛ3Ɛ0 = ((1-ая 3-НТ)-ая 3-НТ)-ая 3-НТ
ηηηη... = 4Ɛ0 = 1-ая 4-НТ
5Ɛ0 = 4Ɛ4Ɛ4Ɛ4Ɛ... = 1-ая 5-НТ
ωƐ0 = 1-ая ω-НТ
1ƐωƐ0+1 = 1-ая НТ после ω-НТ
2ƐωƐ0+1 = 1-ая 2-НТ после ω-НТ
3ƐωƐ0+1 = 1-ая 3-НТ после ω-НТ
ωƐ1 = 2-ая ω-НТ
ωƐω = ω-ая ω-НТ
ωƐ1Ɛ0 = (1-ая НТ)-ая ω-НТ
ωƐ2Ɛ0 = (1-ая 2-НТ)-ая ω-НТ
ωƐ3Ɛ0 = (1-ая 3-НТ)-ая ω-НТ
ωƐωƐ0 = (1-ая ω-НТ)-ая ω-НТ
ωƐωƐ0+1 = ((1-ая ω-НТ)+1)-ая ω-НТ
ωƐ1ƐωƐ0+1 = (1-ая НТ после 1-ая ω-НТ)-ая ω-НТ
ωƐωƐ1 = (2-ая ω-НТ)-ая ω-НТ
ωƐωƐωƐ0 = ((1-ая ω-НТ)-ая ω-НТ)-ая ω-НТ
ω+1Ɛ0 = ωƐωƐωƐωƐ... = 1-ая (ω+1)-НТ
1Ɛ0Ɛ0 = 1-ая (1-ая НТ)-НТ
2Ɛ0Ɛ0 = 1-ая (1-ая 2-НТ)-НТ
3Ɛ0Ɛ0 = 1-ая (1-ая 3-НТ)-НТ
ωƐ0Ɛ0 = 1-ая (1-ая ω-НТ)-НТ
ωƐ0Ɛ0Ɛ0 = 1-ая (1-ая (1-ая ω-НТ)-НТ)-НТ
ωƐ0Ɛ0Ɛ0Ɛ0 = 1-ая (1-ая (1-ая (1-ая ω-НТ)-НТ)-НТ)-НТ
ωƐ0Ɛ0Ɛ0Ɛ0Ɛ0 = 1-ая (1-ая (1-ая (1-ая (1-ая ω-НТ)-НТ)-НТ)-НТ)-НТ
Г0 = ...Ɛ0Ɛ0Ɛ0Ɛ0Ɛ0 = 1-ая гипер-НТ
Ну а чтобы еще лучше понимать все эти рекурсии над ординалами, что мы тут нагородили, давайте попробуем сравнить их с рекурсиями, которые мы создавали на конечных числах. Попытаемся как-то соотнести рекурсивные иерархии неподвижных точек α↦ωα с более привычными для нас арифметическими рекурсиями. Как я уже не раз говорил, и еще раз повторюсь, тетрация с трансфинитным показателем не продвинет нас дальше ωα, потому что ω+1ω = ω+nω = ωε0 = ε0 - для любых n. Однако мы можем изменить правила для ординалов, но сделать это можно только аксиоматически. Итак я ввожу аксиому ω+1ω = ωε0+1, она сдвинет тетрацию с мертвой точки. Как я уже говорил, в разных аксиоматических системах нет ничего страшного, просто у них разные области применимости. Созданная нами аксиома ω+1ω = ωε0+1, лишь переопределяет функцию тетрации, и ее область применения ограничена лишь сравнением рекурсий, поэтому нет ничего страшного в том, что мы применим эту хитрость (хочу отметить, что есть и другие способы сравнить рекурсии над ординалами с высшими арфиметическими действиями). Легко показать, что данная аксиома позволит нам продвинуть высшие арифметические операции над ординалами дальше: ω+2ω = ω(ω+1ω) = ωωε0+1. Так же для наглядности сравнений предлагаю использовать гипероператор для записи высших арифметических действий, а чтобы показать, что рекусии не совсем равны, а скорее, эквивалентны, я буду записывать соотношения так: ωε0+1 ≅ ω[4](ω+1). Напоследок хочу отметить, что арифметические действия, начиная с третьего уровня (степени), считаются с конца, если они идут по порядку и в выражении не расставлены скобки. Ну и не забываем, что уровень арифметического действия так же показывает его приоритет при вычислении.
1 = 0Ɛ0
ω = 0Ɛ1
ω2 = 0Ɛ2 = ω[3]2
ω3 = 0Ɛ3 = ω[3]3
ωω = 0Ɛ0Ɛ0 = ω[3]ω = ω[4]2
ωωω = 0Ɛ0Ɛ0Ɛ0 = ω[3]ω[3]ω = ω[4]3
ωωωω = 0Ɛ0Ɛ0Ɛ0Ɛ0 = ω[3]ω[3]ω[3]ω = ω[4]4
ε0 = ωωωω... = 1Ɛ0 = ω[4]ω
ωε0+1 = 0Ɛ1Ɛ0+1 = ω[4]ω×ω ≅ ω[4](ω+1)
ωε0×2 = 0Ɛ1Ɛ0×2 = ω[4]ω×ω[4]ω
ωωε0+1 = 0Ɛ0Ɛ1Ɛ0+1 = ω[4]ω[3]ω ≅ ω[4](ω+2)
ωωε0×2 = 0Ɛ0Ɛ1Ɛ0×2 = ω[4]ω[3]ω[4]ω
ωωωε0+1 = 0Ɛ0Ɛ0Ɛ1Ɛ0+1 = ω[4]ω[3]ω[4]ω[3]ω ≅ ω[4](ω+3)
ε1 = ε0ε0ε0ε0...= ωωω...ε0+1 = 1Ɛ1 ≅ ω[4](ω×2)
ε2 = ε1ε1ε1ε1...= ωωω...ε1+1= 1Ɛ2 ≅ ω[4](ω×3)
εω = 1Ɛω ≅ ω[4](ω[3]2)
εω+1 = ωωω...εω+1 = 1Ɛω+1 ≅ ω[4](ω[3]2+ω)
εω×2 = 1Ɛω×2 ≅ ω[4](ω[3]2×2)
εω2 = 1Ɛω2 ≅ ω[4](ω[3]3)
εωω = 1Ɛωω ≅ ω[4](ω[3]ω)
εε0 = 1Ɛ1Ɛ0 ≅ ω[4]ω[4]ω = ω[5]2
εεε0 = 1Ɛ1Ɛ1Ɛ0 ≅ ω[4]ω[4]ω[4]ω = ω[5]3
εεεε0 = 1Ɛ1Ɛ1Ɛ1Ɛ0 ≅ ω[4]ω[4]ω[4]ω[4]ω = ω[5]4
ζ0 = εεεε... = 2Ɛ0 ≅ ω[5]ω
ωζ0+1 = 0Ɛ2Ɛ0+1 ≅ ω[5]ω[2]ω
ωωζ0+1 = 0Ɛ0Ɛ2Ɛ0+1 = ω[5]ω[3]ω
εζ0+1 = ζ0ζ0ζ0ζ0...= ωωω...ζ0+1= 1Ɛ2Ɛ0+1 ≅ ω[5]ω[4]ω
ωεζ0+1+1 = 0Ɛ1Ɛ2Ɛ0+1+1 ≅ ω[5]ω[4]ω×ω
ωωεζ0+1+1 = 0Ɛ0Ɛ1Ɛ2Ɛ0+1+1 ≅ ω[5]ω[4]ω[3]ω
εζ0+2 = εζ0+1εζ0+1εζ0+1εζ0+1... = ωωω...εζ0+1+1 = 1Ɛ2Ɛ0+2 ≅ ω[5]ω[4](ω×2)
εζ0+ω = 1Ɛ2Ɛ0+1Ɛ0 ≅ ω[5]ω[4](ω[3]2)
εζ0+ωω = 1Ɛ2Ɛ0+1Ɛ0 ≅ ω[5]ω[4](ω[3]ω)
εζ0+ε0 = 1Ɛ2Ɛ0+1Ɛ0 ≅ ω[5]ω[4]ω[4]ω
εζ0+ε1 = 1Ɛ2Ɛ0+1Ɛ1 ≅ ω[5]ω[4]ω[4](ω×2)
εζ0+εε0 = 1Ɛ2Ɛ0+1Ɛ1Ɛ0 ≅ ω[5]ω[4]ω[5]2
εζ0×2 = 1Ɛ2Ɛ0×2 ≅ ω[5]ω[4]ω[5]ω
εζ0×3 = 1Ɛ2Ɛ0×3 ≅ ω[5]ω[4](ω[5]ω×2)
εζ0×ω = 1Ɛ2Ɛ0×ω ≅ ω[5]ω[4](ω[5]ω×ω)
εεζ0+1 = εζ0ζ0ζ0ζ0...= 1Ɛ1Ɛ2Ɛ0+1 ≅ ω[5]ω[4]ω[5]ω[4]ω
εεεζ0+1 = 1Ɛ1Ɛ1Ɛ2Ɛ0+1 ≅ ω[5]ω[4]ω[5]ω[4]ω[5]ω[4]ω
ζ1 = εεε...ζ0+1= 2Ɛ1 ≅ ω[5](ω×2)
ζ2 = εεε...ζ1+1= 2Ɛ2 ≅ ω[5](ω×3)
ζω = 2Ɛω ≅ ω[5](ω[3]2)
ζωω = 2Ɛωω ≅ ω[5](ω[3]ω)
ζε0 = 2Ɛ1Ɛ0 ≅ ω[5](ω[4]ω)
ζζ0 = 2Ɛ2Ɛ0 ≅ ω[5]ω[5]ω = ω[6]2
ζζζ0= 2Ɛ2Ɛ2Ɛ0 ≅ ω[5]ω[5]ω[5]ω = ω[6]3
η0 = ζζζζ... = 3Ɛ0 ≅ ω[6]ω
ωη0+1 = 0Ɛ3Ɛ0+1 ≅ ω[6]ω[2]ω
εη0+1 = η0η0η0η0... = ωωω...η0+1 = 1Ɛ3Ɛ0+1 ≅ ω[6]ω[4]ω
εη0+2 = εη0+1εη0+1εη0+1εη0+1... = ωωω...εη0+1= 1Ɛ3Ɛ0+2 ≅ ω[6]ω[4](ω×2)
εη0+ε0 = 1Ɛ3Ɛ0+1Ɛ0 ≅ ω[6]ω[4]ω[4]ω
εη0+ζ0 = 1Ɛ3Ɛ0+2Ɛ0 ≅ ω[6]ω[4]ω[5]ω
εη0×2 = 1Ɛ3Ɛ0×2 ≅ ω[6]ω[4]ω[6]ω
εεη0+1 = εη0η0η0η0...= 1Ɛ1Ɛ3Ɛ0+1 ≅ ω[6]ω[4]ω[6]ω[4]ω
εεεη0+1 = 1Ɛ1Ɛ1Ɛ3Ɛ0+1 ≅ ω[6]ω[4]ω[6]ω[4]ω[6]ω[4]ω
ζη0+1 = εεε...η0+1 = 2Ɛ3Ɛ0+1 ≅ ω[6]ω[5]ω
εζη0+1+1 = ζη0+1ζη0+1ζη0+1ζη0+1...= ωωω...ζη0+1+1= 1Ɛ2Ɛ3Ɛ0+1+1 ≅ ω[6]ω[5]ω[4]ω
ζη0+2 = εεε...ζη0+1+1 = 2Ɛ3Ɛ0+2 ≅ ω[6]ω[5](ω×2)
ζη0+ε0 = εεε...ζη0+1+1 = 2Ɛ3Ɛ0+1Ɛ0 ≅ω[6]ω[5](ω[4]ω)
ζη0+ζ0 = εεε...ζη0+1+1 = 2Ɛ3Ɛ0+2Ɛ0 ≅ ω[6]ω[5]ω[5]ω
ζη0×2 = 2Ɛ3Ɛ0×2 ≅ ω[6]ω[5]ω[6]ω
ζεη0+1 = ζη0η0η0η0...= 2Ɛ1Ɛ3Ɛ0+1 ≅ ω[6]ω[5]ω[6](ω[4]ω)
ζζη0+1 = ζεε...η0+1 = 2Ɛ2Ɛ3Ɛ0+1≅ ω[6]ω[5]ω[6]ω[5]ω
ζζζη0+1 = 2Ɛ2Ɛ2Ɛ3Ɛ0+1 ≅ ω[6]ω[5]ω[6]ω[5]ω[6]ω[5]ω
η1 = ζζζ...η0+1= 3Ɛ1 ≅ ω[6](ω×2)
η2 = ζζζ...η1+1 = 3Ɛ2 ≅ ω[6](ω×3)
ηω = 3Ɛω ≅ ω[6](ω[3]2)
ηωω = 3Ɛωω ≅ ω[6](ω[3]ω)
ηε0 = 3Ɛ1Ɛ0 ≅ ω[6](ω[4]ω)
ηζ0 = 3Ɛ2Ɛ0 ≅ ω[6](ω[5]ω)
ηη0 = 3Ɛ3Ɛ0 ≅ ω[6]ω[6]ω = ω[7]2
ηηη0 = 3Ɛ3Ɛ3Ɛ0 ≅ ω[6]ω[6]ω[6]ω = ω[7]3
ηηηη... = 4Ɛ0 ≅ ω[7]ω
5Ɛ0 = 4Ɛ4Ɛ4Ɛ4Ɛ... ≅ ω[8]ω
ωƐ0 ≅ ω[ω]ω
0ƐωƐ0+1 ≅ ω[ω]ω×ω
1ƐωƐ0+1 ≅ ω[ω]ω[4]ω
2ƐωƐ0+1 ≅ ω[ω]ω[5]ω
3ƐωƐ0+1 ≅ ω[ω]ω[6]ω
ωƐ1 ≅ ω[ω](ω×2)
ωƐω ≅ ω[ω](ω[3]2)
ωƐωω ≅ ω[ω](ω[3]ω)
ωƐ1Ɛ0 ≅ ω[ω](ω[4]ω)
ωƐ2Ɛ0 ≅ ω[ω](ω[5]ω)
ωƐ3Ɛ0 ≅ ω[ω](ω[6]ω)
ωƐωƐ0 ≅ ω[ω]ω[ω]ω
ωƐωƐ0+1 ≅ ω[ω](ω[ω]ω+ω)
ωƐ1ƐωƐ0+1 ≅ ω[ω](ω[ω]ω[4]ω)
ωƐωƐ1 ≅ ω[ω]ω[ω](ω×2)
ωƐωƐω ≅ ω[ω]ω[ω](ω[3]2)
ωƐωƐ1Ɛ0 ≅ ω[ω]ω[ω](ω[4]ω)
ωƐωƐωƐ0 ≅ ω[ω]ω[ω]ω[ω]ω
ω+1Ɛ0 = ωƐωƐωƐωƐ... ≅ ω[ω+1]ω
ω×2Ɛ0 ≅ ω[ω×2]ω
ω2Ɛ0 ≅ ω[ω[3]2]ω
ωωƐ0 ≅ ω[ω[3]ω]ω
1Ɛ0Ɛ0 ≅ ω[ω[4]ω]ω
2Ɛ0Ɛ0 ≅ ω[ω[5]ω]ω
3Ɛ0Ɛ0 ≅ ω[ω[6]ω]ω
ωƐ0Ɛ0 ≅ ω[ω[ω]ω]ω
ωƐ0Ɛ0Ɛ0 ≅ ω[ω[ω[ω]ω]ω]ω
ωƐ0Ɛ0Ɛ0Ɛ0 ≅ ω[ω[ω[ω[ω]ω]ω]ω]ω
ωƐ0Ɛ0Ɛ0Ɛ0Ɛ0 ≅ ω[ω[ω[ω[ω[ω]ω]ω]ω]ω]ω
Г0 = ...Ɛ0Ɛ0Ɛ0Ɛ0Ɛ0 ≅ ω[...[ω[ω[ω[ω[ω]ω]ω]ω]ω]...]ω - где ω - вложений
Однако однозначные аналогии возможны только до отметки Г0, которая эквивалентна бесконечному вложению гипероператоров с ω. Дальше рекурсивные процедуры, которые приведены в рассмотренных нами нотациях для конечных чисел (будь то расширенный гипероператор, цепная нотация, или массивная нотация, становятся неопределенным для трансфинитных ординалов), в частности из-за того что в основе большинства рекурсий используется n-1, что не работает с ординалами: ω-1 = ω. Это приводит к тому, что фундаментальные последовательности для ординалов могут определяться по разному, даже если мы так же аксиоматически переопределим правила этих нотаций. Значит, в зависимости от того какую нотацию мы взяли для конечных чисел и какую нотацию используем для записи ординалов, результаты сравнений будут отличаться, поэтому начиная с этого момента сопоставление нотаций для чисел и нотаций для ординалов лишено всякого смысла.
Вообще ординал Г0 не просто так имеет собственное имя (Ординал Фефермана-Шутте), да и все именные ординалы - это какие-то важные рубежи в ординальном анализе. Чтобы объяснить чем важен Г0, давайте в начале разберемся в какой системе аксиом мы вообще выстраиваем все эти рекурсии.
Ну логично предположить, что раз ε0 является пределом для Арифметики первого порядка, то рекурсии бо́льшего уровня должны определяться в Арифметике второго порядка[170]. Давайте же разберем, что это значит. Арифметика первого порядка так называлась, потому что она оперировала в качестве переменных только натуральными числами. Если мы позволим в качестве переменных использовать не только числа, но и множества состоящие из натуральных чисел, то такие множества будут переменными второго порядка. Все аксиомы из Арифметики Пеано, кроме аксиомы индукции, мы без изменений перенесем в нашу новую систему аксиом. Аксиому индукции изменим так, чтобы она работала не только с натуральными числами, но и с множествами натуральных чисел. Еще нам необходимо добавить то, что называют Аксиомой свертывания второго порядка (Second-order comprehension axiom), которая гласит, что всякое выделение подмножества в множестве натуральных чисел равносильно некой формуле заданной на этом подмножестве. Эта аксиома похожа на аксиомы выделения и преобразования из теории множеств, она так же определяет принципы работы с множествами, и так же, по сути, является схемой для создания других аксиом или теорем. Ее отличительной особенностью в арифметике второго порядка является то, что она применима исключительно к множествам натуральных чисел. Другая важная функция этой аксиомы в том, что она четко разграничивает переменные первого порядка (натуральные числа) и переменные второго порядка (множества натуральных чисел), утверждая что формулы с натуральными числами могут быть равносильны множествам натуральных чисел, но не являются ими. Возможно звучит немного запутанно, но без этой аксиомы, возникает парадокс, когда натуральное число может принадлежать и не принадлежать некому множеству одновременно. Если призадуматься, то в этой аксиоме можно даже увидеть глубокий философский смысл, действительно способ описания или восприятия объекта не является самим объектом, и как бы подробно не воспринималась или описывалась бы нами действительность, мы всегда воспринимаем и описываем лишь проекции объектов. А еще, что будет для нас очень важно в дальнейшем, согласно аксиоме свертывания получается, что любой формуле заданной на натуральных числах можно сопоставить множество. Так же хочу подчеркнуть, что такая система аксиом не будет теорией множеств, потому что оперировать мы можем только множествами из натуральных чисел, и поскольку в систему аксиом не будет включена аксиома множества всех подмножеств, то все множества Арифметики второго порядка будут счетными (имеющие кардинальность ℵ0).
приложение 13 (аксиомы арифметики второго порядка)
Арифметика второго порядка (условно обозначается так: Z2) получается очень сильной аксиоматической системой. Уровень рекурсий, который она допускает и может доказуемо описать, намного намного намного больше тех рекурсий, которыми мы сейчас оперируем. Более того в рамках этой книги я не смогу (да и никто наверное не сможет) вот так же детально расписать предел Арифметики второго порядка, как я это сделал с пределом Арифметики первого порядка, мы сможем лишь приблизительно к нему подобраться, уже не разбирая всю суть рекурсий, которые создаются вблизи него (хочу заметить, что аксиомы теории множеств ZFC - будут еще сильнее). Однако арифметику второго порядка так же как и арифметику первого порядка тоже можно разбить на подсистемы, и чаще всего так и делают, потому что полностью охватить ее возможности невероятно сложно, да и в принципе то не нужно, поскольку большинство теорем, для которых необходимы множества натуральных чисел, можно сформулировать и доказать в рамках более слабых подсистем арифметики второго порядка. Мы же помним основной принцип, которого теперь придерживаются математики, после того как Гедель совершил переворот в философии математики своей теоремой о неполноте: "Не существует абсолютной системы аксиом и у каждой системы своя область применимости".
Так вот в Арифметике второго порядка можно выделить подсистему, которая будет эквивалента Примитивно-рекурсивной арифметике (PRA), такая система будет называться Аксиомами рекурсивного свертывания, по-английски: Recursive Comprehension Axioms (RCA0)[171], создается она очень просто, путем ограничения аксиомы индукции и аксиомы свертывания только для примитивно-рекурсивных функций, по-сути мы так же поступали, создавая Примитивно-рекурсивную арифметику (PRA) из арифметики Пеано (PA). Только в ней не было аксиомы свертывания, потому что там не было множеств натуральных чисел. Здесь и далее, так же хочу пояснить, что ноль в аббревиатуре подсистемы означает, что аксиома индукции сформулирована так, как она звучала в арифметике первого порядка, то есть множества натуральных чисел в ее определении не фигурируют. Ну и получается, что RCA0 в отношении доказательно-рекурсивной силы эквивалентна PRA, за тем лишь исключением, что в ней есть множества натуральных чисел, хоть аксиома индукции на них и не распространяется. Соответственно рекурсивным пределом для RCA0 так же как для PRA будет являться ωω, он и будет PTO этой подсистемы.
Кроме того мы можем выделить подсистему, которая будет эквивалента Арифметике первого порядка, ограничив аксиомы индукции и аксиомы свертывания только для арифметических функций и формул, тогда такая подсистема будет называться Аксиомами арифметического свертывания, по-английски: Arithmetical comprehension axioms (ACA0)[171] и будет иметь тот же рекурсивный предел: PTO ACA0 = ε0, что и Арифметика первого порядка.
И вот теперь мы добрались до подсистемы, PTO которой будет равен Г0. Выделим такую подсистему, в которой аксиома индукции (по-прежнему ограниченная тем, что сформулирована на языке первого порядка) может повторяться трансфинтное число раз. Это будет значить что ее формулировка: "утверждение верное для n и для n+1, будет верно для всех натуральных чисел" будет расширенна тем, что "n может быть не только натуральным числом, но и трансфинитным ординалом, а значит инудкция распространяется и на них". Грубо говоря это будет первая арифметическая система аксиом, которая сможет оперировать ординалами и трансфинитной индукцией. То есть, можно сказать, что мы в какой-то степени объявляем о существовании бесконечности, но поскольку аксиома индукции в этом случае не распространяется на множества, то в нашей системе аксиом существуют только ординалы, и никаких других бесконечных множеств. Называться эта подсистема будет Арифметической трансфинитной рекурсией, по-английски: Arithmetical Transfinite Recursion (ATR0)[171]. То есть в более слабых системах, например в Арифметике первого порядка, невозможно было показать даже существование ω - первого трансфинитного ординала, ведь, как я говорил во второй части, бесконечность в арифметике подразумевается, но не существует как объект, которым можно оперировать. То как мы измеряли ординалами рекурсивную способность более слабых систем, например установив, что PTO PA = ε0, не считается, потому что, на самом деле, мы производили эти измерения в более сильных аксиоматических системах, например мы могли бы это делать в ATR0 (ведь это подсистема Арифметики второго порядка, в которой заявлено о существовании ординалов). Однако уровень рекурсий над ординалами в ATR0 будет ограничен арифметическими рекурсивными формулами. Так, например, рекурсию ординалов уровня Г0 уже невозможно описать средствами ATR0, следовательно это и будет PTO для этой подсистемы[169], ну а Г0 подставленный в функцию быстрорастущей иерархии или в функцию иерархии Харди создаст максимально возможную рекурсию на натуральных числах в рамках ATR0.
Именно поэтому кстати рекурсии над ординалами и рекурсии над конечными числами однозначно можно сопоставить только до уровня Г0. Это можно показать еще одним интересным способом. Давайте переопределим функцию быстрорастущей иерархии так, чтобы она работала с ординалами. Формально это будет записываться так: fα(β) = ∪γ<αfγ(β), где α - предельный ординал. Давайте разберем на примерах как будет работать такая функция:
f0(ω) = ω+1
f1(ω) = ω×2
f2(ω) = ω×2ω = ω×ω = ω2
f3(ω) = ω×ω×ω×... = ωω
f4(ω) = ε0
f5(ω) = ζ0
f6(ω) = η0
fω(ω) = ωƐ0
ff0(ω)(ω) = ω+1Ɛ0
ff1(ω)(ω) = ω×2Ɛ0
ff2(ω)(ω) = ω2Ɛ0
ff3(ω)(ω) = ωωƐ0
ff4(ω)(ω) = 1Ɛ0Ɛ0
ffω(ω)(ω) = ωƐ0Ɛ0
fffω(ω)(ω)(ω) = ωƐ0Ɛ0Ɛ0
ffffω(ω)(ω)(ω)(ω) = ωƐ0Ɛ0Ɛ0Ɛ0
fffffω(ω)(ω)(ω)(ω)(ω) = ωƐ0Ɛ0Ɛ0Ɛ0Ɛ0
α↦fα(ω) = fffff...(ω)(ω)(ω)(ω)(ω) = ...Ɛ0Ɛ0Ɛ0Ɛ0Ɛ0 = Г0
Такое схождение рекурсий приводит к интересному выводу: любая иерархия представляющая собой семейство функций, нумерацию которых можно продолжить трансфинитными ординалами, так чтобы в рекурсиях функции были задействованы их фундаментальные последовательности, не превзойдет по силе fГ0(n). На этом этапе большинство семейств иерархических функций, какие бы правила мы не придумывали (не привлекая в эти правила ординалы, а используя их только в фундаментальных последовательностях) испытают примерное схождение в своей рекурсивной силе. Поэтому если вы вдруг захотите создать свою собственную иерархию, которая по вашему мнению будет сильнее быстрорастущей иерархии, помните это следствие.
Ну а мы отправляемся за пределы подсистемы ATR0. Как следует из определения, раз Г0 - это первая неподвижная точка для функции α↦αƐ0, то должна существовать и вторая неподвижная точка Г1, но учитывая уровень рекурсий, сдвинуться с неподвижной точки Г0 и добраться до Г1 будет непросто, ведь Г0 будет неподвижной точкой и для более слабых рекурсивных функций, таких как ωn, εn, ωƐn, nƐ0, значит теперь уже ωГ0 = εГ0 = ωƐГ0 = Г0Ɛ0 = Г0. Но мы попытаемся... Начнем так, как мы это делали с предыдущими неподвижными точками, которые встречались на нашем пути, будем постепенно наращивать меньшие рекурсии на бо́льшем ординале, попутно давая названия ординалам относительно функции α↦ωα, пользуясь принятым ранее сокращением ("НТ" - "неподвижная точка функции α↦ωα"), и посмотрим куда нас это приведет.
Г0+1
ωГ0+1 = 0ƐГ0+1 = Г0×ω
εГ0+1 = 1ƐГ0+1 = ωωω...Г0+1 = Г0Г0Г0Г0... = 1-ая НТ после 1-ой гипер-НТ
ζГ0+1 = 2ƐГ0+1 = εεε...Г0+1 = 1-ая 2-НТ после 1-ой гипер-НТ
ηГ0+1 = 3ƐГ0+1 = ζζζ...Г0+1 = 1-ая 3-НТ после 1-ой гипер-НТ
ωƐГ0+1 = 1-ая ω-НТ после 1-ой гипер-НТ
ωƐ0ƐГ0+1 = 1-ая (1-ая ω-НТ)-НТ после 1-ой гипер-НТ
ωƐ0Ɛ0ƐГ0+1 = 1-ая (1-ая (1-ая ω-НТ)-НТ)-НТ после 1-ой гипер-НТ
ωƐ0Ɛ0Ɛ0ƐГ0+1 = 1-ая (1-ая (1-ая (1-ая ω-НТ)-НТ)-НТ)-НТ после 1-ой гипер-НТ
...Ɛ0Ɛ0Ɛ0Ɛ0ƐГ0+1 = 1-ая (1-ая (1-ая (1-ая (...)-НТ)-НТ)-НТ)-НТ после 1-ой гипер-НТ
Казалось бы вот она заветная Г1, но нет ...Ɛ0Ɛ0Ɛ0Ɛ0ƐГ0+1 ≠ Г1. И даже ...Ɛ0Ɛ0Ɛ0Ɛ0ƐГ0+1 ≠ Г0ƐГ0+1, хотя казалось бы (...Ɛ0Ɛ0Ɛ0Ɛ0)ƐГ0+1 - в скобках явно находится Г0, но ординальная арифметика не позволяет нам поставить скобки таким образом, и то что находится в скобках нельзя рассматривать отдельно от всего выражения. Вспомните как мы уже сталкивались с чем-то подобным ωƐ1 = sup(nƐωƐ0+1|n<ω) ≠ ωƐωƐ0+1. Здесь работает тот же принцип, предел последовательности натуральных чисел нельзя рассматривать отдельно от всего выражения: sup(f(n)|n<ω) ≠ f(ω) при условии наличия меньших рекурсий на бо́льшем ординале. Ординальные неподвижные точки тоже достигаются как пределы последовательностей, где натуральными числами можно обозначить уровень самовложенности, поэтому их так же нельзя рассматривать отдельно от выражения при условии наличия меньших рекурсий на бо́льшем ординале. Соответственно, ...Ɛ0Ɛ0Ɛ0Ɛ0ƐГ0+1 < Г0ƐГ0+1 < Г1 и равно это выражение будет лишь: ...Ɛ0Ɛ0Ɛ0Ɛ0ƐГ0+1 = Г0Ɛ1. Правильно записать его необходимо следующим образом: sup(nƐГ0+1|n<Г0) = Г0Ɛ1. С названием этого ординала тоже, кажется на первый взляд, не все в порядке. Он будет называться "1ая (1ая гипер-НТ)-НТ после 1ой гипер-НТ" или "2ая (1ая гипер-НТ)-НТ". Здесь хочет спросить, а разве "1ая (1ая гипер-НТ)-НТ" по определению не должна быть равна просто "1ой гипер-НТ". Все верно, но мы вырвали эту часть определения из конекста, а в контексте всего определения было слово "... после ...", что явно намекает на наличие меньших рекурсий на бо́льшем ординале, так что с определением все в порядке. К тому же кажестя логичным что если "1ая (1ая гипер-НТ)-НТ = 1ая гипер-НТ", следовательно "1ая (1ая гипер-НТ)-НТ после 1ой гипер-НТ = 1ая (1ая гипер-НТ)-НТ после 1ой (1ая гипер-НТ)-НТ = 2-ая (1ая гипер-НТ)-НТ > 1ая (1ая гипер-НТ)-НТ". Да, и если вы внимательно следили за сокращенными определениями, которые я приводил ранее в списке, вы уже могли встретить нечто подобное, например: εζ0+ζ0 = εζ0×2 = "(1-ая 2-НТ)-ая НТ после 1-ой 2-НТ", где вот эта часть "(1-ая 2-НТ)-ая НТ" без конекста так же по определению равна просто "1-ой 2-НТ". Возвращаясь к нашему Г0Ɛ1, можно уверждать, что этот ординал не является неподвижной точкой для α↦αƐ0, потому что Г0Ɛ1Ɛ0 ≠ Г0Ɛ1 (ординал Г0Ɛ1Ɛ0 намного больше, чем Г0Ɛ1, но все же меньше чем Г1). Ну а до настоящей Г1 - второй неподвижной точки α↦αƐ0 нам еще очень далеко. Так что давайте продолжать свое восхождение к ней.
Г0 = ...Ɛ0Ɛ0Ɛ0Ɛ0Ɛ0 = 1-ая гипер-НТ = 1ая (1-ая гипер-НТ)-НТ
Г0Ɛ1 = ...Ɛ0Ɛ0Ɛ0Ɛ0ƐГ0+1 = 1ая (1-ая гипер-НТ)-НТ после 1ой гипер-НТ = 2ая (1-ая гипер-НТ)-НТ
εГ0Ɛ1+1 = 1ƐГ0Ɛ1+1 = ωωω...Г0Ɛ1+1 = 1-ая НТ после 2ой (1-ая гипер-НТ)-НТ
ζГ0Ɛ1+1 = 2ƐГ0Ɛ1+1 = εεε...Г0Ɛ1+1 = 1-ая 2-НТ после 2ой (1-ая гипер-НТ)-НТ
ηГ0Ɛ1+1 = 3ƐГ0Ɛ1+1 = ζζζ...Г0Ɛ1+1 = 1-ая 3-НТ после 2ой (1-ая гипер-НТ)-НТ
ωƐГ0Ɛ1+1 = 1-ая ω-НТ после 2ой (1-ая гипер-НТ)-НТ
ωƐ0ƐГ0Ɛ1+1 = 1-ая (1-ая ω-НТ)-НТ после 2ой (1-ая гипер-НТ)-НТ
ωƐ0Ɛ0ƐГ0Ɛ1+1 = 1-ая (1-ая (1-ая ω-НТ)-НТ)-НТ после 2ой (1-ая гипер-НТ)-НТ
ωƐ0Ɛ0Ɛ0ƐГ0Ɛ1+1 = 1-ая (1-ая (1-ая (1-ая ω-НТ)-НТ)-НТ)-НТ после 2ой (1-ая гипер-НТ)-НТ
...Ɛ0Ɛ0Ɛ0Ɛ0ƐГ0Ɛ1+1 = Г0Ɛ2 = 1-ая (1-ая (1-ая (1-ая (...)-НТ)-НТ)-НТ)-НТ после 2ой (1-ая гипер-НТ)-НТ
Дальше продолжаем наращивать рекурсии уже на этих промежуточных пределах, никакой из которых все так же не является второй неподвижной точкой α↦αƐ0, они по-прежнему по отношению к этой функции будут лишь n-ными пределами α↦αƐ0, меньшими чем вторая неподвижная точка α↦αƐ0. На этом пути нам, как раз, и встретится Г0ƐГ0+1, который, как мы помним, должен, быть намного больше чем ...Ɛ0Ɛ0Ɛ0Ɛ0ƐГ0+1 = Г0Ɛ1.
Г0Ɛ1 = 1ая (1-ая гипер-НТ)-НТ после 1ой гипер-НТ = 2ая (1-ая гипер-НТ)-НТ
Г0Ɛ2 = 2ая (1-ая гипер-НТ)-НТ после 1ой гипер-НТ = 3ья (1-ая гипер-НТ)-НТ
Г0Ɛω = Г0Ɛ0Ɛ0 = ω-ая (1-ая гипер-НТ)-НТ
Г0Ɛε0 = Г0Ɛ1Ɛ0 = (1-ая НТ)-ая (1-ая гипер-НТ)-НТ
Г0Ɛζ0 = Г0Ɛ2Ɛ0 = (1-ая 2-НТ)-ая (1-ая гипер-НТ)-НТ
Г0Ɛη0 = Г0Ɛ3Ɛ0 = (1-ая 3-НТ)-ая (1-ая гипер-НТ)-НТ
Г0ƐωƐ0 = (1-ая ω-НТ)-ая (1-ая гипер-НТ)-НТ
Г0ƐωƐ0Ɛ0 = (1-ая (1-ая ω-НТ)-НТ)-ая (1-ая гипер-НТ)-НТ
Г0ƐωƐ0Ɛ0Ɛ0 = (1-ая (1-ая (1-ая ω-НТ)-НТ)-НТ)-ая (1-ая гипер-НТ)-НТ
Г0Ɛ...Ɛ0Ɛ0Ɛ0Ɛ0 = Г0ƐГ0 = (1-ая гипер-НТ)-ая (1-ая гипер-НТ)-НТ
Г0Ɛ...Ɛ0Ɛ0Ɛ0Ɛ0+1 = Г0ƐГ0+1 = (1-ая гипер-НТ + 1)-ая (1-ая гипер-НТ)-НТ
Г0ƐГ0+ω = (1-ая гипер-НТ + ω)-ая (1-ая гипер-НТ)-НТ
Г0ƐωГ0+1 = Г0Ɛ0ƐГ0+1 = (1-ая гипер-НТ × ω)-ая (1-ая гипер-НТ)-НТ
Г0ƐεГ0+1 = Г0Ɛ1ƐГ0+1 = (1-ая НТ после 1-ой гипер-НТ)-ая (1-ая гипер-НТ)-НТ
Г0ƐГ0Ɛ1 = Г0Ɛ...Ɛ0Ɛ0Ɛ0ƐГ0+1 = (2-ая (1-ая гипер-НТ)-НТ)-ая (1-ая гипер-НТ)-НТ
Г0ƐГ0ƐГ0= ((1-ая гипер-НТ)-ая (1-ая гипер-НТ)-НТ)-ая (1-ая гипер-НТ)-НТ
Г0ƐГ0ƐГ0ƐГ0= (((1-ая гипер-НТ)-ая (1-ая гипер-НТ)-НТ)-ая (1-ая гипер-НТ)-НТ)-ая (1-ая гипер-НТ)-НТ
Г0+1Ɛ0 = Г0ƐГ0ƐГ0Ɛ... = (((...)-ая (1-ая гипер-НТ)-НТ)-ая (1-ая гипер-НТ)-НТ)-ая (1-ая гипер-НТ)-НТ
А сейчас на нашем пути встретился еще один вид промежуточных ординалов, которые еще по-прежнему не являются последующими неподвижными точками α↦αƐ0, а значит до Г1 все еще далеко, но нам остался уже последний рывок. Давайте пока разберемся чем является Г0ƐГ0ƐГ0Ɛ..., и с чем-то подобным мы уже многократно сталкивались. Так например, ωωωω... = 0Ɛ0Ɛ0Ɛ0Ɛ... - это первая 1-неподвижная точка α↦ωα, εεεε... = 1Ɛ1Ɛ1Ɛ1Ɛ... - это первая 2-неподвижная точка α↦ωα, ζζζζ... = 2Ɛ2Ɛ2Ɛ2Ɛ... - это первая 3-неподвижная точка α↦ωα. Получается, что Г0ƐГ0ƐГ0Ɛ... = Г0+1Ɛ0 - это следующая n-неподвижная точка α↦ωα после 1-ой неподвижной точки α↦αƐ0, или ее можно назвать 1-ая (Г0+1)-неподвижная точка α↦ωα. И действительно, если 1-ая (Г0)-неподвижная точка α↦ωα - это просто Г0, как следует из ее определения: Г0Ɛ0 = Г0, то это же самое нельзя сказать про Г0+1Ɛ0 (потому что Г0+1Ɛ0 > Г0+1), значит этот ординал не является неподвижной точкой для α↦αƐ0, и меньше чем Г1 - вторая неподвижная точка этой функции, поскольку до нее мы еще не добрались. Но, как я и сказал, нам остался последний рывок.
Г0+1Ɛ1 = Г0ƐГ0Ɛ...Г0+1Ɛ0+1 = 1-ая (1-ая гипер-НТ + 1)-НТ
Г0+2Ɛ0 = Г0+1ƐГ0+1ƐГ0+1Ɛ... = 1-ая (1-ая гипер-НТ + 2)-НТ
ωГ0+1Ɛ0 = 0ƐГ0+1Ɛ0 = 1-ая (1-ая гипер-НТ × ω)-НТ
εГ0+1Ɛ0 = 1ƐГ0+1Ɛ0 = 1-ая (1-ая НТ после 1-ой гипер-НТ)-НТ
ζГ0+1Ɛ0 = 2ƐГ0+1Ɛ0 = 1-ая (1-ая 2-НТ после 1-ой гипер-НТ)-НТ
ηГ0+1Ɛ0 = 3ƐГ0+1Ɛ0 = 1-ая (1-ая 3-НТ после 1-ой гипер-НТ)-НТ
ωƐГ0+1Ɛ0 = 1-ая (1-ая ω-НТ после 1-ой гипер-НТ)-НТ
...Ɛ0Ɛ0Ɛ0ƐГ0+1Ɛ0 = Г0Ɛ1Ɛ0 = 1-ая (2-ая (1-ая гипер-НТ)-НТ)-НТ
Г0+1Ɛ0Ɛ0 = Г0ƐГ0ƐГ0ƐГ...Ɛ0 = 1-ая (1-ая (1-ая гипер-НТ + 1)-НТ)-НТ
...Ɛ0Ɛ0ƐГ0+1Ɛ0Ɛ0 = Г0Ɛ1Ɛ0Ɛ0 = 1-ая (1-ая (2-ая (1-ая гипер-НТ)-НТ)-НТ)-НТ
Г0+1Ɛ0Ɛ0Ɛ0 = Г0ƐГ0ƐГ...Ɛ0Ɛ0 = 1-ая (1-ая (1-ая (1-ая гипер-НТ + 1)-НТ)-НТ)-НТ
Г0+1...Ɛ0Ɛ0Ɛ0 = Г1 = 1-ая (1-ая (1-ая (1-ая ...(1-ая гипер-НТ + 1)... -НТ)-НТ)-НТ)-НТ
Наконец-то добрались до второй неподвижной точки α↦αƐ0 или второй гипер-неподвижной точки α↦ωα. Несложно проверить, что Г0+1...Ɛ0Ɛ0Ɛ0 = Г1, ведь если мы подставим ординал Г0+1...Ɛ0Ɛ0Ɛ0 в функцию α↦αƐ0, то получим Г0+1...Ɛ0Ɛ0Ɛ0Ɛ0 - что в общем-то тоже самое. Ну а за ней сразу перейдем к третьей неподвижной точке Г2 = Г1+1...Ɛ0Ɛ0Ɛ0, а там и пошло и поехало, продолжим нумерацию неподвижных точек α↦αƐ0 всеми известными нам ординалами: Г0; Г1; Г2; Гω; Гε0; ГГ0; ГГГ0; ГГГГ... . И вот на нашем пути новая фисированная точка уровня α↦Гα, ну а по отношению к функции α↦ωα можно сказать что это 1-ая 2-гипер-неподвижная точка. Для нумерации таких неподвижных точек можно придумать новую букву или поступить так как мы делали с заглавной эпсилон (1Ɛn = εn; 2Ɛn = ζn; 3Ɛn = ηn и т.д.), добавить нашей заглавной букве гамма еще один индекс, и нумерация неподвижных точек α↦Гα будет выглядеть так 1Г0, 1Г1, 1Гω , ... 1Г1Г1Г1Г.... По отношению к функции α↦ωα это будут n-ые 2-гипер-неподвижные точки. И здесь вновь возникают фисированные точки бо́льшего уровня: α↦1Гα, которые будем нумеровать уже так 2Гn. Думаю основную схему все уже поняли: n+1Г0 = nГnГnГnГ.... По отношению к функции α↦ωα такие построения соответствуют n-гипер-неподвижным точкам. Ну а дальше можем уже встраивать иерархию их ординалов на этих боковых индексах: Г0Г0 = ...Ɛ0Ɛ0Ɛ0Ɛ0Г0; Г0Г0Г0 = ...Ɛ0Ɛ0Ɛ0Г0Г0; Г0Г0Г0Г0 = ...Ɛ0Ɛ0Г0Г0Г0; создавая тем самым трансфинитную рекурсию на n-гипер-неподвижности функции α↦ωα; пока не дойдем до ...Г0Г0Г0Г0, которая будет первой неподвижной точкой α↦αГ0.
Дальше мы можем придумать новую заглавную греческую букву, например, P0 (Ро-ноль), чтобы сделать для α↦αГ0 иерархию аналогичную той, которую мы так долго выше выстраивали для α↦αƐ0. Так чтобы ...Г0Г0Г0Г0 = P0; P0+1...Г0Г0Г0 = P1; 1P0 = PPPP... и в конечном счете получим ординал: ...P0P0P0P0. Для нумерации неподвижных точек, которого нам опять понадобиться новая заглавная греческая буква, пусть будет B0 (Бета-ноль), но поскольку общая схема создания таких ординалов уже ясна, то тут опять может возникнуть дефицит греческих букв, как это было с εn, ζn, ηn, ..., но нам уже тогда не хватит заглавных букв. Конечно мы так же можем придумать для их нумерации новый вид индексов, например писать его сверху. По отношению к функции α↦ωα нам так же потребуется минимум три характеристики для именования неподвижных точек. Смотрите сами: mƐn - m-ная n-неподвижная точка α↦ωα, mГn - m-ная n-гипер-неподвижная точка α↦ωα, mPn - m-ная n-гипер2-неподвижная точка α↦ωα, mBn - m-ная n-гипер3-неподвижная точка α↦ωα, и так далее, выстраивая иерархию из m-ных n-гиперk-неподвижных точек α↦ωα. Но и в направлении третьего индекса можно создавать еще более высокоуровневые неподвижные точки, первая из которых будет называться Ординалом Аккермана (Ackermann ordinal)[172], но тогда запись ординалов станет невероятно громоздкой. Рано или поздно мы запутаемся во всех этих буквах и индексах исходящих во всех направлениях, поэтому давайте будем считать, что на этом Расширенная ординальная нотация Кантора себя исчерпала, и нам нужен другой способ для записи ординалов.
Никто не спорит, что Расширенная нотация Катора очень наглядная, но из-за обилия всех этих греческих букв и индексов, торчащих в разные стороны, сложно написать для нее единые лаконичные правила, которые отражали бы что она вполне упорядочена. А значит и создание таких же кратких и лаконичных фундаментальных последовательностей (для их последующего использования в функциях быстрорастущей иерархи) на основе этой нотации будет сопряжено с теми же трудностями. Фундаментальные последовательности для стандартной ординальной нотации Кантора выше мы записали всего в пяти строчках, для расширенной же ординальной нотации Кантора фундаментальные последовательности придется дописывать каждый раз, как только мы вводим новую греческую букву или новый индекс к ней, что очень неудобно. Нам нужна новая, более универсальная ординальная нотация, в которой бы заранее были учтены ее расширения, что позволит лаконично определить все ее фундаментальные последовательности, чтобы рекурсии заложенные в ординалах с легкостью переносились на рекурсии над конечными числами.
Если бы мы с вами создавали более мощную нотацию, соответствующую вышеописанным требованиям, нашей главной целью стало бы правильное учитывание всех неподвижных точек. Благо изобретать такую нотацию нам с вами не придется, это сделал еще в 1908 году американский математик Освальд Веблен[173]. Работает эта нотация на основе его функции, которая так и называется Функцией Веблена. Функция представляет собой массив из аргументов - φ(a,b,c,...), где каждый аргумент в сущности являет собой номер некой неподвижной точки, при этом сами аргументы тоже могут быть трансфинитными ординалами. Такой способ учета ординалов в виде массива называют Иерархией Веблена, позже он будет использоваться нами и в других более мощных нотациях.
Очень сложно в двух словах описать как работает Функция Веблена, лучше показать это на примерах. Но готовьтесь к тому, что перечень примеров будет очень большой, ведь мы будем сопоставлять все уже рассмотренные нами ординалы с их записью в виде Функции Веблена. Внимательно изучите этот список, понимание Функции Веблена будет необходимо для осознания рекурсий, которые я буду давать в дальнейшем. Перед примерами я приведу законченное формальное определение Функции Веблена. Там же будут приведены фундаментальные последовательности, определенные для всех видов предельных счетных ординалов, которые могут возникать в нотации (напомню что фундаментальные последовательности, как раз, и являются способом переложения ординальных рекурсий на конечные числа). Однако ни для этой ни для других ординальных функций далее, я не буду разбирать их подробно, вам достаточно знать, что они существуют и базируются на законченном формальном определении функции, которое гарантирует, что ординальная нотация является вполне упорядоченной, то есть учитывает каждый ординал от нуля и до своего предела, а значит и корректно определенный вычислительный процесс, использующий фундаментальные последовательности будет гарантировано работать без прерываний и зацикливаний. Вместо детального изучения фундаментальных последовательностей мы лучше будем изучать поэтапное построение ординалов в сравнении с их выражением в предыдущей нотации, это даст намного более наглядное понимание того как будут работать заложенные в них рекурсии.
Так же стоит упомянуть очень важную вещь, Функция Веблена, которая формально будет описана ниже, на самом деле еще не является полноценной ординальной нотацией, так же как не будет являться полноценной ординальной нотацией ни одна ординальная функция описанная ниже. Поскольку другим важным требованием к ординальной нотации, помимо наличия упорядоченности и нормальной формы, является законченное описание отношений принадлежности между ординалами[174]. По определению ординалы это такие упорядоченные множества, которые включают в себя все предыдущие ординалы как элементы. Следовательно, если взять два разных ординала, то один из них обязательно должен быть элементом другого, или как говорят математики, должен принадлежать ему. Получается, что тот ординал, который принадлежит будет меньше, а тот к которому он принадлежит будет больше. Поэтому, грубо говоря, алгоритм описывающий отношение принадлежности между ординалами выражаемыми ординальной функцией это просто формальный способ определить какой из двух ординалов больше. Значит для ординалов отношения "∈" и "<" являются эквивалентными. Но имейте ввиду, что для множеств не являющихся ординалами отношение "<" может быть бессмысленным. Например, попробуйте определить, какое из двух множеств больше A = {ω×2, ω×4, ω9} или B = {ω×6, ω2, ω3, ω4}, и вы поймете, что понятие "больше" тут не вполне определено. Даже поиск максимального элемента в множестве может не иметь смысла, ведь элементы неординальных множеств тоже могут быть не ординалами. У множеств не являющихся ординалами можно измерить только их кардинальность, то есть количество элементов и сравнить ее между собой, например |B| > |A|. Поэтому для любых произвольных множеств алгоритм отношения принадлежности не существует.
Однако для любой системы работающей только с ординалами (ординальной нотации), в которой есть нормальная форма, с помощью которой можно записать каждый ординал до предела нотации, алгоритм отношения принадлежности должен существовать. Написание такого алгоритма под нормальные формы ординальных функций это пожалуй самая сложная часть при создании ординальной нотации. Строгое формальное определение алгоритма отношения принадлежности нужно прежде всего для компьютеров, которые будут работать с фундаментальными последовательностями, при вычислении рекурсий для создания сверхбольших чисел. Дело в том, что компьютеры не понимают, что такое ординалы, и не могут работать с актуальными бесконечностями, для них необходимо переписать фундаментальные последовательности как некие строковые переменные связанные между собой рекурсивными правилами. То есть компьютер при вычислении будет работать не с ординалами, а со строками, которые представляют собой нормальную форму записи ординала, и значит он должен уметь их как-то сравнивать между собой, здесь ему на помощь и придет формальный алгоритм отношения принадлежности, без него вычисление числа невозможно.
В формальном определении функции я не привожу этот алгоритм, однако его можно найти в трудах авторов изначально определивших данные ординальные функции, и это уже удел профессинальной математики и серьезной теории доказательств, который нам по правде и не нужен. Тем не менее, если вы подробно изучите примеры ординалов, приведенные ниже, то вы получите достаточное интуитивное понимание, того как должен работать алгоритм описывающий отношение принадлежности между ординалами. Ведь, по сути, этот алгоритм должен учитывать два основных важных момента[174]. Первый: если перед нами очередной ординал, то мы должны понять как записывается предшествующий ему, и эта процедура очень простая, особенно если в нотации присутствует операция сложения – любому ординалу α+n, предшествует α+(n-1) , где n - натуральное число, больше нуля. Второй: если перед нами предельный ординал, то мы должны понять предел какой бесконечной фундаментальной последовательности из ординалов может его создавать, вот эта задача намного сложнее, и как раз ее решение для некоторых частных случаев я и демонстрирую в таблице, поняв которые вы уловите основной принцип ординальной нотации.
Обычно после создания такого алгоритма, определение фундаментальных последовательностей сводится лишь к тому, чтобы привязать их нему, что весьма тривиальная задача. Мы же с вами поступим наоборот, сразу определим фундаментальные последовательности, так что с небольшими изменениями на их основе можно будет определить алгоритм отношения принадлежности. Следовательно наше определение ординальной функции гарантирует, что такой алгоритм может быть эффективно создан. Нам достататочно того, что ординальная функция генерирует вполне упорядоченные ординалы, которые можно выразить конечным способом в виде нормальной формы, и на нее основе мы можем определить фундаментальные последовательности необходимые чтобы создавать большие зарекурсированные конечные числа.
Функция Веблена (Veblen function)
Определение:
z - это пустая строка, либо строка содержащая один или несколько нулей 0,0,0,...0
s - это пустая строка, либо строка содержащая один или несколько ординалов α
1,α
2,...,α
n
Z - это пустая строка, либо строка содержащая один или несколько нулей
0β10β20β3 ...
0βn
S - это пустая строка, либо строка содержащая один или несколько ординалов
α1β1α2β2...
αnβn
где α
1 > 0; β
n - обратно упорядоченные, неповторяющиеся ординалы
Функция:
φ(γ) = ωγ
φ(z,s,γ) = φ(s,γ)
φ(ZS
γ0) = φ(S
γ0)
Если
αn+1 > 0, где
n ≥ 0, тогда:
φ(s,αn+1,z,γ) обозначает (1+γ)-ую неподвижную точку функции
ξ↦φ(s,β,ξ,z) для каждого
β < αn+1
φ(S
αn+1γ0) обозначает (1+γ)-ую неподвижную точку функции ξ↦φ(S
βn+1ξn) для каждого β < α
n+1
Если α
> 0, n - предельный ординал, тогда:
φ(S
αnγ0) обозначает (1+γ)-ый предел
sup(φ(S
αkγ0)|k<n)
Нормальная форма:
0 - записан в нормальной форме.
Ненулевой ординал (меньший Малого ординала Вебелна) должен быть записан в нормальной форме функции Веблена с конечным порядковым числом аргументов:
α = φ(s1)+φ(s2)+...+φ(sk), где:
1.
φ(s1) ≥ φ(s2) ≥ ... ≥ φ(sk)
2. s
m - произвольная строка ординалов
αm,1 , αm,2 , ... , αm,nm где m∈{1,...,k}
3.
αm,1 > 0 и αm,i < φ(sm) для
m∈{1,...,k} и i∈{1,..,nm}
4.
k, n1, ... , nk - натуральные числа
Ненулевой ординал (меньший Большого ординала Вебелна) так же должен быть записан в нормальной форме функции Веблена с трансфинитным порядковым числом аргументов:
α = φ(α1,1β1,1 ...... α1,n1β1,n1)+φ(α2,1β2,1 ...... α2,n2β2,n2)+...+φ(αk,1βk,1 ...... αk,nkβk,nk), где:
1. k-ный ординал второй строки
βk ≥ 0 определяет позицию k-ного ординала первой строки
αk > 0 в строке аргуменов функции Веблена.
2.
φ(α1,1β1,1 ...... α1,n1β1,n1) ≥ φ(α2,1β2,1 ...... α2,n2β2,n2) ≥ ... ≥ φ(αk,1βk,1 ...... αk,nkβk,nk)
3.
αm,i < φ(αm,1βm,1 ...... αm,nmβm,nm) для всех m∈{1,...,k} и i∈{1,..,nm}
4.
βm,i < φ(αm,1βm,1 ...... αm,nmβm,nm) для всех m∈{1,...,k} и i∈{1,..,nm}
5.
φ(αk,1βk,1 ...... αk,nkβk,nk) - предельный ординал
6.
k, n1, ... , nk - натуральные числа
Свойства:
Если n - натуральное число:
φ(1,n) - (n+1)-ная неподвижная точка α↦φ(α) или ωωωω... = εn
φ(2,n) - (n+1)-ная неподвижная точка α↦φ(1,α) или εεεε... = ζn
φ(3,n) - (n+1)-ная неподвижная точка α↦φ(2,α) или ζζζζ... = ηn
φ(m+1,n) - (n+1)-ная неподвижная точка α↦φ(m,α) или mƐmƐmƐmƐ... = m+1Ɛn
φ(1,0,n) - (n+1)-ная неподвижная точка α↦φ(α,0) или ...Ɛ0Ɛ0Ɛ0Ɛ0Ɛ0 = Гn
φ(1,m+1,n) - (n+1)-ная неподвижная точка α↦φ(1,m,α) или mГmГmГmГ... = m+1Гn
φ(2,0,n) - (n+1)-ная неподвижная точка α↦φ(1,α,0) или ...Г0Г0Г0Г0Г0 = Pn
φ(3,0,n) - (n+1)-ная неподвижная точка α↦φ(2,α,0) или ...P0P0P0P0P0 = Bn
φ(m+1,0,n) - (n+1)-ная неподвижная точка α↦φ(m,α,0)
φ(1,0,0,n) - (n+1)-ная неподвижная точка α↦φ(α,0,0)
и т.д.
Если n - трансфинитный ординал:
φ(1,n) - n-ная неподвижная точка α↦φ(α) или ω
ωωω... = ε
n
φ(2,n) - n-ная неподвижная точка α↦φ(1,α) или ε
εεε... = ζ
n
φ(3,n) - n-ная неподвижная точка α↦φ(2,α) или ζ
ζζζ... = η
n
φ(m+1,n) - n-ная неподвижная точка α↦φ(m,α) или
mƐ
mƐmƐmƐ... =
m+1Ɛ
n
φ(1,0,n) - n-ная неподвижная точка α↦φ(α,0) или
...Ɛ0Ɛ0Ɛ0Ɛ0Ɛ
0 = Г
n
φ(1,m+1,n) - n-ная неподвижная точка α↦φ(1,m,α) или
mГ
mГmГmГ... =
m+1Г
n
φ(2,0,n) - n-ная неподвижная точка α↦φ(1,α,0) или
...Г0Г0Г0Г0Г
0 = P
n
φ(3,0,n) - n-ная неподвижная точка α↦φ(2,α,0) или
...P0P0P0P0P
0 = B
n
φ(m+1,0,n) - n-ная неподвижная точка α↦φ(m,α,0)
φ(1,0,0,n) - n-ная неподвижная точка α↦φ(α,0,0)
и т.д.
Фундаментальные последовательности[175]:
для функции с конечным порядковым числом аргументов:
1. (φ(s1)+φ(s2)+...+φ(sk))[n] = φ(s1)+φ(s2)+...+φ(sk)[n]
2. φ(γ)[n] = n, если γ = 1
3. φ(γ)[n] = φ(γ-1)×n, если γ - очередной ординал
4. φ(γ)[n] = φ(γ[n]), если γ - предельный ординал
5. φ(s,α,z,γ)[0] = 0, если γ = 0 и α - очередной ординал
6. φ(s,α,z,γ)[n+1] = φ(s,α-1,φ(s,α,z,γ)[n],z), если γ = 0 и α - очередной ординал
7. φ(s,α,z,γ)[0] = φ(s,α,z,γ-1)+1, если γ и α - очередные ординалы
8. φ(s,α,z,γ)[n+1] = φ(s,α-1,φ(s,α,z,γ)[n],z), если γ и α - очередные ординалы
9. φ(s,α,z,γ)[n] = φ(s,α,z,γ[n]), если γ - предельный ординал
10. φ(s,α,z,γ)[n] = φ(s,α[n],z,γ), если γ = 0, α - предельный ординал
11. φ(s,α,z,γ)[n] = φ(s,α[n],φ(s,α,z,γ-1)+1,z), если γ - очередной ординал и α - предельный ординал
для функции с трансфинитным порядковым числом аргументов:
1. (φ(α1,1β1,1 ...... α1,n1β1,n1)+φ(α2,1β2,1 ...... α2,n2β2,n2)+...+φ(αk,1βk,1 ...... αk,nkβk,nk))[n] =
φ(α1,1β1,1 ...... α1,n1β1,n1)+φ(α2,1β2,1 ...... α2,n2β2,n2)+...+φ(αk,1βk,1 ...... αk,nkβk,nk)[n]
2. φ(γ0)[n] = n, если γ = 1
3. φ(γ0)[n] = φ(γ-10)×n, если γ - очередной ординал
4. φ(γβ)[n] = φ(γ[n]β), если γ - предельный ординал
5. φ(γβ)[n] = φ(γ-1βφ(γ-1β)+1β[n]), если γ - очередной ординал и β - предельный ординал
6. φ(γβ)[n+1] = φ(γ-1βφ(γβ)[n]β-1), если γ и β - очередные ординалы
7. φ(Sαβγ0)[0] = 0, если γ = 0 и α - очередной ординал
8. φ(Sαβγ0)[n+1] = φ(Sα-1βφ(Sαβγ-10)+1β[n]), если γ = 0 и α - очередной ординал и β - предельный ординал
9. φ(Sαβγ0)[n+1] = φ(Sα-1βφ(Sαβγ0)[n]β-1), если γ = 0 и α и β - очередные ординалы
10. φ(Sαβγ0)[0] = φ(Sαβγ-10)+1, если γ и α - очередные ординалы
11. φ(Sαβγ0)[n+1] = φ(Sα-1βφ(Sαβγ-10)+1β[n]), если γ и α - очередные ординалы и β - предельный ординал
12. φ(Sαβγ0)[n+1] = φ(Sα-1βφ(Sαβγ0)[n]β-1), если γ и α и β - очередные ординалы
13. φ(Sαβγ0)[n] = φ(Sαβγ[n]0), если γ - предельный ординал
14. φ(Sαβγ0)[n] = φ(Sα[n]βγ0), если γ = 0, α - предельный ординал
15. φ(Sαβγ0)[n] = φ(Sα[n]βφ(Sαβγ-10)+1β[n]), если γ - очередной ординал, α и β - предельные ординалы
16. φ(Sαβγ0)[n] = φ(Sα[n]βφ(Sαβγ-10)+1β-1), если γ и β - очередные ординалы и α - предельный ординал
17. α[0] = 0 и α[n+1] = φ(1α[n]), если α = min{β|φ(1β) = β}
Первоначальное авторство: Освальд Веблен, 1908 год
[173].
Последующая модификация: Курт Шутте, 1954 год
[176].
приложение 14 (Функция Веблена)
| 1 = ω0 = 0Ɛ0 |
φ(0) |
| 2 |
φ(0)+φ(0) |
| 3 |
φ(0)+φ(0)+φ(0) |
| ω = ω1 = 0Ɛ1 |
φ(0)+φ(0)+φ(0)+... = φ(1) = φ(φ(0)) |
| ω+1 |
φ(1)+φ(0) |
| ω+2 |
φ(1)+φ(0)+φ(0) |
| ω+3 |
φ(1)+φ(0)+φ(0)+φ(0) |
| ω+ω = ω×2 |
φ(1)+φ(0)+φ(0)+φ(0)+... = φ(1)+φ(1) |
| ω×2+1 |
φ(1)+φ(1)+φ(0) |
| ω×2+2 |
φ(1)+φ(1)+φ(0)+φ(0) |
| ω×2+3 |
φ(1)+φ(1)+φ(0)+φ(0)+φ(0) |
| ω×2+ω = ω×3 |
φ(1)+φ(1)+φ(0)+φ(0)+φ(0)+... = φ(1)+φ(1)+φ(1) |
| ω×3+1 |
φ(1)+φ(1)+φ(1)+φ(0) |
| ω×3+2 |
φ(1)+φ(1)+φ(1)+φ(0)+φ(0) |
| ω×3+3 |
φ(1)+φ(1)+φ(1)+φ(0)+φ(0)+φ(0) |
| ω×3+ω = ω×4 |
φ(1)+φ(1)+φ(1)+φ(0)+φ(0)+φ(0)+... = φ(1)+φ(1)+φ(1)+φ(1) |
| ω×5 |
φ(1)+φ(1)+φ(1)+φ(1)+φ(1) |
| ω×6 |
φ(1)+φ(1)+φ(1)+φ(1)+φ(1)+φ(1) |
| ω2 = ω×ω = 0Ɛ2 |
φ(2) = φ(1)+φ(1)+φ(1)+φ(1)+φ(1)+φ(1)+... |
| ω2+1 |
φ(2)+φ(0) |
| ω2+2 |
φ(2)+φ(0)+φ(0) |
| ω2+3 |
φ(2)+φ(0)+φ(0)+φ(0) |
| ω2+ω |
φ(2)+φ(1) |
| ω2+ω+1 |
φ(2)+φ(1)+φ(0) |
| ω2+ω+2 |
φ(2)+φ(1)+φ(0)+φ(0) |
| ω2+ω×2 |
φ(2)+φ(1)+φ(1) |
| ω2+ω×3 |
φ(2)+φ(1)+φ(1)+φ(1) |
| ω2×2 |
φ(2)+φ(2) |
| ω2×2+1 |
φ(2)+φ(2)+φ(0) |
| ω2×2+2 |
φ(2)+φ(2)+φ(0)+φ(0) |
| ω2×2+ω |
φ(2)+φ(2)+φ(1) |
| ω2×2+ω+1 |
φ(2)+φ(2)+φ(1)+φ(0) |
| ω2×2+ω×2 |
φ(2)+φ(2)+φ(1)+φ(1) |
| ω2×3 |
φ(2)+φ(2)+φ(2) |
| ω2×4 |
φ(2)+φ(2)+φ(2)+φ(2) |
| ω3 = ω2×ω = 0Ɛ3 |
φ(3) = φ(2)+φ(2)+φ(2)+φ(2)+... |
| ω3+1 |
φ(3)+φ(0) |
| ω3+ω |
φ(3)+φ(1) |
| ω3+ω2 |
φ(3)+φ(2) |
| ω3×2 |
φ(3)+φ(3) |
| ω3×3 |
φ(3)+φ(3)+φ(3) |
| ω4 = ω3×ω = 0Ɛ4 |
φ(4) = φ(3)+φ(3)+φ(3)+... |
| ω5 = ω4×ω = 0Ɛ5 |
φ(5) = φ(4)+φ(4)+φ(4)+... |
| ωω = 0Ɛω |
φ(ω) = φ(φ(1)) = φ(φ(0)+φ(0)+φ(0)+...) |
| ωω+1 |
φ(φ(1))+φ(0) |
| ωω+2 |
φ(φ(1))+φ(0)+φ(0) |
| ωω+ω |
φ(φ(1))+φ(1) |
| ωω+ω+1 |
φ(φ(1))+φ(1)+φ(0) |
| ωω+ω×2 |
φ(φ(1))+φ(1)+φ(1) |
| ωω+ω×2+1 |
φ(φ(1))+φ(1)+φ(1)+φ(0) |
| ωω+ω×3 |
φ(φ(1))+φ(1)+φ(1)+φ(1) |
| ωω+ω2 |
φ(φ(1))+φ(2) |
| ωω+ω2+1 |
φ(φ(1))+φ(2)+φ(0) |
| ωω+ω2+ω |
φ(φ(1))+φ(2)+φ(1) |
| ωω+ω2×2 |
φ(φ(1))+φ(2)+φ(2) |
| ωω+ω3 |
φ(φ(1))+φ(3) |
| ωω×2 |
φ(φ(1))+φ(φ(1)) |
| ωω×2+1 |
φ(φ(1))+φ(φ(1))+φ(0) |
| ωω×2+ω |
φ(φ(1))+φ(φ(1))+φ(1) |
| ωω×2+ω2 |
φ(φ(1))+φ(φ(1))+φ(2) |
| ωω×2+ω3 |
φ(φ(1))+φ(φ(1))+φ(3) |
| ωω×3 |
φ(φ(1))+φ(φ(1))+φ(φ(1)) |
| ωω+1 = ωω×ω |
φ(φ(1)+φ(0)) = φ(φ(1))+φ(φ(1))+φ(φ(1))+... |
| ωω+1+1 |
φ(φ(1)+φ(0))+φ(0) |
| ωω+1+ω |
φ(φ(1)+φ(0))+φ(1) |
| ωω+1+ω2 |
φ(φ(1)+φ(0))+φ(2) |
| ωω+1+ω3 |
φ(φ(1)+φ(0))+φ(3) |
| ωω+1+ωω |
φ(φ(1)+φ(0))+φ(φ(1)) |
| ωω+1+ωω×2 |
φ(φ(1)+φ(0))+φ(φ(1))+φ(φ(1)) |
| ωω+1×2 |
φ(φ(1)+φ(0))+φ(φ(1)+φ(0)) |
| ωω+1×3 |
φ(φ(1)+φ(0))+φ(φ(1)+φ(0))+φ(φ(1)+φ(0)) |
| ωω+2 = ωω+1×ω |
φ(φ(1)+φ(0)+φ(0)) |
| ωω+2+ωω |
φ(φ(1)+φ(0)+φ(0))+φ(φ(1)) |
| ωω+2+ωω+1 |
φ(φ(1)+φ(0)+φ(0))+φ(φ(1)+φ(0)) |
| ωω+2×2 |
φ(φ(1)+φ(0)+φ(0))+φ(φ(1)+φ(0)+φ(0)) |
| ωω+3 |
φ(φ(1)+φ(0)+φ(0)+φ(0)) |
| ωω×2 |
φ(φ(1)+φ(1)) |
| ωω×2+1 |
φ(φ(1)+φ(1))+φ(0) |
| ωω×2+ωω |
φ(φ(1)+φ(1))+φ(φ(1)) |
| ωω×2+ωω+1 |
φ(φ(1)+φ(1))+φ(φ(1))+φ(0) |
| ωω×2+ωω×2 |
φ(φ(1)+φ(1))+φ(φ(1))+φ(φ(1)) |
| ωω×2+ωω+1 |
φ(φ(1)+φ(1))+φ(φ(1)+φ(0)) |
| ωω×2+ωω+1+1 |
φ(φ(1)+φ(1))+φ(φ(1)+φ(0))+φ(0) |
| ωω×2+ωω+1+ωω |
φ(φ(1)+φ(1))+φ(φ(1)+φ(0))+φ(φ(1)) |
| ωω×2+ωω+1×2 |
φ(φ(1)+φ(1))+φ(φ(1)+φ(0))+φ(φ(1)+φ(0)) |
| ωω×2+ωω+2 |
φ(φ(1)+φ(1))+φ(φ(1)+φ(0)+φ(0)) |
| ωω×2×2 |
φ(φ(1)+φ(1))+φ(φ(1)+φ(1)) |
| ωω×2+1 = ωω×2×ω |
φ(φ(1)+φ(1)+φ(0)) = φ(φ(1)+φ(1))+φ(φ(1)+φ(1))+φ(φ(1)+φ(1))+... |
| ωω×2+1+1 |
φ(φ(1)+φ(1)+φ(0))+φ(0) |
| ωω×2+1+ωω |
φ(φ(1)+φ(1)+φ(0))+φ(φ(1)) |
| ωω×2+1+ωω×2 |
φ(φ(1)+φ(1)+φ(0))+φ(φ(1)+φ(1)) |
| ωω×2+1×2 |
φ(φ(1)+φ(1)+φ(0))+φ(φ(1)+φ(1)+φ(0)) |
| ωω×2+2 = ωω×2+1×ω |
φ(φ(1)+φ(1)+φ(0)+φ(0)) |
| ωω×3 |
φ(φ(1)+φ(1)+φ(1)) |
| ωω×4 |
φ(φ(1)+φ(1)+φ(1)+φ(1)) |
| ωω2 = ωω×ωω×ωω×... |
φ(φ(2)) = φ(φ(1)+φ(1)+φ(1)+...) |
| ωω2+1 |
φ(φ(2))+φ(0) |
| ωω2+ωω |
φ(φ(2))+φ(φ(1)) |
| ωω2+ωω+1 |
φ(φ(2))+φ(φ(1)+φ(0)) |
| ωω2+ωω×2 |
φ(φ(2))+φ(φ(1)+φ(1)) |
| ωω2+ωω×2+1 |
φ(φ(2))+φ(φ(1)+φ(1)+φ(0)) |
| ωω2+ωω×3 |
φ(φ(2))+φ(φ(1)+φ(1)+φ(1)) |
| ωω2×2 |
φ(φ(2))+φ(φ(2)) |
| ωω2+1 = ωω2×ω |
φ(φ(2)+φ(0)) = φ(φ(2))+φ(φ(2))+φ(φ(2))+... |
| ωω2+ω |
φ(φ(2)+φ(1)) |
| ωω2+ω×2 |
φ(φ(2)+φ(1)+φ(1)) |
| ωω2×2 |
φ(φ(2)+φ(2)) |
| ωω2×3 |
φ(φ(2)+φ(2)+φ(2)) |
| ωω2×4 |
φ(φ(2)+φ(2)+φ(2)+φ(2)) |
| ωω3 = ωω2×ωω2×ωω2×... |
φ(φ(3)) = φ(φ(2)+φ(2)+φ(2)+...) |
| ωω4 = ωω3×ωω3×ωω3×... |
φ(φ(4)) = φ(φ(3)+φ(3)+φ(3)+...) |
| ωωω |
φ(φ(ω)) = φ(φ(φ(1))) |
| ωωω+1 |
φ(φ(φ(1)))+φ(0) |
| ωωω+ω |
φ(φ(φ(1)))+φ(1) |
| ωωω+ωω |
φ(φ(φ(1)))+φ(φ(1)) |
| ωωω+ωω2 |
φ(φ(φ(1)))+φ(φ(2)) |
| ωωω×2 |
φ(φ(φ(1)))+φ(φ(φ(1))) |
| ωωω+1 = ωωω×ω |
φ(φ(φ(1))+φ(0)) = φ(φ(φ(1)))+φ(φ(φ(1)))+φ(φ(φ(1)))+... |
| ωωω+ω |
φ(φ(φ(1))+φ(1)) |
| ωωω+ω2 |
φ(φ(φ(1))+φ(2)) |
| ωωω×2 |
φ(φ(φ(1))+φ(φ(1))) |
| ωωω×3 |
φ(φ(φ(1))+φ(φ(1))+φ(φ(1))) |
| ωωω+1 = ωωω×ω |
φ(φ(φ(1)+φ(0))) = φ(φ(φ(1))+φ(φ(1))+φ(φ(1))+...) |
| ωωω+1+1 |
φ(φ(φ(1)+φ(0)))+φ(0) |
| ωωω+1+ωω |
φ(φ(φ(1)+φ(0)))+φ(φ(1)) |
| ωωω+1+ωωω |
φ(φ(φ(1)+φ(0)))+φ(φ(φ(1))) |
| ωωω+1×2 |
φ(φ(φ(1)+φ(0)))+φ(φ(φ(1)+φ(0))) |
| ωωω+1+1 |
φ(φ(φ(1)+φ(0))+φ(0)) |
| ωωω+1+ω |
φ(φ(φ(1)+φ(0))+φ(1)) |
| ωωω+1+ωω |
φ(φ(φ(1)+φ(0))+φ(φ(1))) |
| ωωω+1×2 |
φ(φ(φ(1)+φ(0))+φ(φ(1)+φ(0))) |
| ωωω+1×3 |
φ(φ(φ(1)+φ(0))+φ(φ(1)+φ(0))+φ(φ(1)+φ(0))) |
| ωωω+2 |
φ(φ(φ(1)+φ(0)+φ(0))) |
| ωωω+3 |
φ(φ(φ(1)+φ(0)+φ(0)+φ(0))) |
| ωωω×2 |
φ(φ(φ(1)+φ(1))) |
| ωωω×2+1 |
φ(φ(φ(1)+φ(1)))+φ(0) |
| ωωω×2+ωωω |
φ(φ(φ(1)+φ(1)))+φ(φ(φ(1))) |
| ωωω×2×2 |
φ(φ(φ(1)+φ(1)))+φ(φ(φ(1)+φ(1))) |
| ωωω×2+1 |
φ(φ(φ(1)+φ(1))+φ(0)) |
| ωωω×2+1 |
φ(φ(φ(1)+φ(1)+φ(0))) |
| ωωω×2+2 |
φ(φ(φ(1)+φ(1)+φ(0)+φ(0))) |
| ωωω×3 |
φ(φ(φ(1)+φ(1)+φ(1))) |
| ωωω2 = ωωω×ωω×ωω×... |
φ(φ(φ(2))) = φ(φ(φ(1)+φ(1)+φ(1)+...)) |
| ωωω2+1 |
φ(φ(φ(2)))+φ(0) |
| ωωω2×2 |
φ(φ(φ(2)))+φ(φ(φ(2))) |
| ωωω2+1 |
φ(φ(φ(2))+φ(0)) |
| ωωω2+ωω |
φ(φ(φ(2))+φ(φ(1))) |
| ωωω2×2 |
φ(φ(φ(2))+φ(φ(2))) |
| ωωω2+1 |
φ(φ(φ(2)+φ(0))) |
| ωωω2+2 |
φ(φ(φ(2)+φ(0)+φ(0))) |
| ωωω2+ω |
φ(φ(φ(2)+φ(1))) |
| ωωω2+ω+1 |
φ(φ(φ(2)+φ(1)+φ(0))) |
| ωωω2+ω×2 |
φ(φ(φ(2)+φ(1)+φ(1))) |
| ωωω2×2 |
φ(φ(φ(2)+φ(2))) |
| ωωω3= ωωω2×ωω2×ωω2×... |
φ(φ(φ(3))) = φ(φ(φ(2)+φ(2)+φ(2)+...)) |
| ωωω4= ωωω3×ωω3×ωω3×... |
φ(φ(φ(4))) = φ(φ(φ(3)+φ(3)+φ(3)+...)) |
| ωωωω |
φ(φ(φ(ω))) = φ(φ(φ(φ(1)))) |
| ωωωω+1 |
φ(φ(φ(φ(1))))+φ(0) |
| ωωωω×2 |
φ(φ(φ(φ(1))))+φ(φ(φ(φ(1)))) |
| ωωωω+1 |
φ(φ(φ(φ(1)))+φ(0)) |
| ωωωω×2 |
φ(φ(φ(φ(1)))+φ(φ(φ(1)))) |
| ωωωω+1 |
φ(φ(φ(φ(1))+φ(0))) |
| ωωωω×2 |
φ(φ(φ(φ(1))+φ(φ(1)))) |
| ωωωω+1 |
φ(φ(φ(φ(1)+φ(0)))) |
| ωωωω×2 |
φ(φ(φ(φ(1)+φ(1)))) |
| ωωωω2 |
φ(φ(φ(φ(2)))) = φ(φ(φ(φ(1)+φ(1)+φ(1)+...))) |
| ωωωω3 |
φ(φ(φ(φ(3)))) = φ(φ(φ(φ(2)+φ(2)+φ(2)+...))) |
| 5ω = ωωωωω |
φ(φ(φ(φ(ω)))) = φ(φ(φ(φ(φ(1))))) |
| 6ω = ωωωωωω |
φ(φ(φ(φ(φ(ω))))) = φ(φ(φ(φ(φ(φ(1)))))) |
| ωω = ωωωωωω... = ε0 = 1Ɛ0 |
φ(1,0) = φ(φ(φ(φ(φ(φ(φ(φ(...)))))))) |
| ε0+1 |
φ(1,0)+φ(0) |
| ε0+2 |
φ(1,0)+φ(0)+φ(0) |
| ε0+3 |
φ(1,0)+φ(0)+φ(0)+φ(0) |
| ε0+ω |
φ(1,0)+φ(1) |
| ε0+ω+1 |
φ(1,0)+φ(1)+φ(0) |
| ε0+ω×2 |
φ(1,0)+φ(1)+φ(1) |
| ε0+ω2 |
φ(1,0)+φ(2) |
| ε0+ω2+1 |
φ(1,0)+φ(2)+φ(0) |
| ε0+ω2+ω |
φ(1,0)+φ(2)+φ(1) |
| ε0+ω2×2 |
φ(1,0)+φ(2)+φ(2) |
| ε0+ω3 |
φ(1,0)+φ(3) |
| ε0+ωω |
φ(1,0)+φ(φ(1)) |
| ε0+ωω+1 |
φ(1,0)+φ(φ(1))+φ(0) |
| ε0+ωω+ω |
φ(1,0)+φ(φ(1))+φ(1) |
| ε0+ωω+ω2 |
φ(1,0)+φ(φ(1))+φ(2) |
| ε0+ωω×2 |
φ(1,0)+φ(φ(1))+φ(φ(1)) |
| ε0+ωω+1 |
φ(1,0)+φ(φ(1)+φ(0)) |
| ε0+ωω+1+1 |
φ(1,0)+φ(φ(1)+φ(0))+φ(0) |
| ε0+ωω+1+ωω |
φ(1,0)+φ(φ(1)+φ(0))+φ(φ(1)) |
| ε0+ωω+1×2 |
φ(1,0)+φ(φ(1)+φ(0))+φ(φ(1)+φ(0)) |
| ε0+ωω+2 |
φ(1,0)+φ(φ(1)+φ(0)+φ(0)) |
| ε0+ωω×2 |
φ(1,0)+φ(φ(1)+φ(1)) |
| ε0+ωω×3 |
φ(1,0)+φ(φ(1)+φ(1)+φ(1)) |
| ε0+ωω2 |
φ(1,0)+φ(φ(2)) |
| ε0+ωω3 |
φ(1,0)+φ(φ(3)) |
| ε0+ωωω |
φ(1,0)+φ(φ(φ(1))) |
| ε0+ωωω+1 |
φ(1,0)+φ(φ(φ(1)))+φ(0) |
| ε0+ωωω+1 |
φ(1,0)+φ(φ(φ(1))+φ(0)) |
| ε0+ωωω+1 |
φ(1,0)+φ(φ(φ(1)+φ(0))) |
| ε0+ωωω×2 |
φ(1,0)+φ(φ(φ(1)+φ(1))) |
| ε0+ωωω2 |
φ(1,0)+φ(φ(φ(2))) |
| ε0+ωωω3 |
φ(1,0)+φ(φ(φ(3))) |
| ε0+ωωωω |
φ(1,0)+φ(φ(φ(φ(1)))) |
| ε0+ωωωω+1 |
φ(1,0)+φ(φ(φ(φ(1))))+φ(0) |
| ε0+ωωωω+1 |
φ(1,0)+φ(φ(φ(φ(1)))+φ(0)) |
| ε0+ωωωω+1 |
φ(1,0)+φ(φ(φ(φ(1))+φ(0))) |
| ε0+ωωωω+ω |
φ(1,0)+φ(φ(φ(φ(1))+φ(1))) |
| ε0+ωωωω×2 |
φ(1,0)+φ(φ(φ(φ(1))+φ(φ(1)))) |
| ε0+ωωωω+1 |
φ(1,0)+φ(φ(φ(φ(1)+φ(0)))) |
| ε0+ωωωω×2 |
φ(1,0)+φ(φ(φ(φ(1)+φ(1)))) |
| ε0+ωωωω2 |
φ(1,0)+φ(φ(φ(φ(2)))) |
| ε0+ωωωωω |
φ(1,0)+φ(φ(φ(φ(φ(1))))) |
| ε0+ωωωωωω |
φ(1,0)+φ(φ(φ(φ(φ(φ(1)))))) |
| ε0+ωωωωωω... = ε0×2 |
φ(1,0)+φ(φ(φ(φ(φ(φ(...)))))) = φ(1,0)+φ(1,0) |
| ε0×2+1 |
φ(1,0)+φ(1,0)+φ(0) |
| ε0×2+ω |
φ(1,0)+φ(1,0)+φ(1) |
| ε0×2+ωω |
φ(1,0)+φ(1,0)+φ(φ(1)) |
| ε0×2+ωωω |
φ(1,0)+φ(1,0)+φ(φ(φ(1))) |
| ε0×2+ωωωω |
φ(1,0)+φ(1,0)+φ(φ(φ(φ(1)))) |
| ε0×3 |
φ(1,0)+φ(1,0)+φ(1,0) |
| ε0×4 |
φ(1,0)+φ(1,0)+φ(1,0)+φ(1,0) |
| ε0×ω = ωε0+1 |
φ(φ(1,0)+1) = φ(φ(1,0)+φ(0)) = φ(1,0)+φ(1,0)+φ(1,0)+... |
| ε0×(ω+1) = ωε0+1+ε0 |
φ(φ(1,0)+1)+φ(1,0) |
| ε0×(ω×2) = ωε0+1×2 |
φ(φ(1,0)+1)+φ(φ(1,0)+1) |
| ε0×ω2 = ωε0+2 |
φ(φ(1,0)+2) = φ(φ(1,0)+1)+φ(φ(1,0)+1)+... |
| ε0×ω3 = ωε0+3 |
φ(φ(1,0)+3) = φ(φ(1,0)+2)+φ(φ(1,0)+2)+... |
| ε0×ωω = ωε0+ω |
φ(φ(1,0)+φ(1)) |
| ε0×(ωω+1) = ωε0+ω+ε0 |
φ(φ(1,0)+φ(1))+φ(1,0) |
| ε0×(ωω+ω) = ωε0+ω+ωε0+1 |
φ(φ(1,0)+φ(1))+φ(φ(1,0)+1) |
| ε0×(ωω×2) = ωε0+ω×2 |
φ(φ(1,0)+φ(1))+φ(φ(1,0)+φ(1)) |
| ε0×ωω+1 = ωε0+ω+1 |
φ(φ(1,0)+φ(1)+1) |
| ε0×ωω×2 = ωε0+ω×2 |
φ(φ(1,0)+φ(1)+φ(1)) |
| ε0×ωω2 = ωε0+ω2 |
φ(φ(1,0)+φ(2)) |
| ε0×ωωω = ωε0+ωω |
φ(φ(1,0)+φ(φ(1))) |
| ε0×ωωωω = ωε0+ωωω |
φ(φ(1,0)+φ(φ(φ(1)))) |
| ε0×ωωωωω = ωε0+ωωωω |
φ(φ(1,0)+φ(φ(φ(φ(1))))) |
| ε02 = ωε0×2 |
φ(φ(1,0)+φ(1,0)) |
| ε02×2 = ωε0×2×2 |
φ(φ(1,0)+φ(1,0))+φ(φ(1,0)+φ(1,0)) |
| ε02×ω = ωε0×2+1 |
φ(φ(1,0)+φ(1,0)+1) |
| ε02×ωω = ωε0×2+ω |
φ(φ(1,0)+φ(1,0)+φ(1)) |
| ε02×ωωω = ωε0×2+ωω |
φ(φ(1,0)+φ(1,0)+φ(φ(1))) |
| ε02×ωωωω = ωε0×2+ωωω |
φ(φ(1,0)+φ(1,0)+φ(φ(φ(1)))) |
| ε03 = ωε0×3 |
φ(φ(1,0)+φ(1,0)+φ(1,0)) |
| ε0ω = ωωε0+1 |
φ(φ(φ(1,0)+1)) |
| ε0ω+1 = ωωε0+1+1 |
φ(φ(φ(1,0)+1))+1 |
| ε0ω+ω = ωωε0+1+ω |
φ(φ(φ(1,0)+1))+φ(1) |
| ε0ω+ωω = ωωε0+1+ωω |
φ(φ(φ(1,0)+1))+φ(φ(1)) |
| ε0ω+ε0 = ωωε0+1+ε0 |
φ(φ(φ(1,0)+1))+φ(1,0) |
| ε0ω+ε0×2 = ωωε0+1+ε0×2 |
φ(φ(φ(1,0)+1))+φ(1,0)+φ(1,0) |
| ε0ω+ε0×ω = ωωε0+1+ωε0+1 |
φ(φ(φ(1,0)+1))+φ(φ(1,0)+1) |
| ε0ω+ε0×ωω = ωωε0+1+ωε0+ω |
φ(φ(φ(1,0)+1))+φ(φ(1,0)+φ(1)) |
| ε0ω+ε02 = ωωε0+1+ωε0×2 |
φ(φ(φ(1,0)+1))+φ(φ(1,0)+φ(1,0)) |
| ε0ω×2 = ωωε0+1×2 |
φ(φ(φ(1,0)+1))+φ(φ(φ(1,0)+1)) |
| ε0ω×ω = ωωε0+1+1 |
φ(φ(φ(1,0)+1)+1) |
| ε0ω×ωω = ωωε0+1+ω |
φ(φ(φ(1,0)+1)+φ(1)) |
| ε0ω+1 = ωωε0+1+ε0 |
φ(φ(φ(1,0)+1)+φ(1,0)) |
| ε0ω+1×ω = ωωε0+1+ε0+1 |
φ(φ(φ(1,0)+1)+φ(1,0)+1) |
| ε0ω+2 = ωωε0+1+ε0+ε0 |
φ(φ(φ(1,0)+1)+φ(1,0)+φ(1,0)) |
| ε0ω×2 = ωωε0+1×2 |
φ(φ(φ(1,0)+1)+φ(φ(1,0)+1)) |
| ε0ω×3 = ωωε0+1×3 |
φ(φ(φ(1,0)+1)+φ(φ(1,0)+1)+φ(φ(1,0)+1)) |
| ε0ω2 = ωωε0+2 |
φ(φ(φ(1,0)+2)) |
| ε0ωω = ωωε0+ω |
φ(φ(φ(1,0)+φ(1))) |
| ε0ωω+1 = ωωε0+ω+1 |
φ(φ(φ(1,0)+φ(1)+1)) |
| ε0ωω×2 = ωωε0+ω×2 |
φ(φ(φ(1,0)+φ(1)+φ(1))) |
| ε0ωω2 = ωωε0+ω2 |
φ(φ(φ(1,0)+φ(2))) |
| ε0ωω2+1 = ωωε0+ω2+1 |
φ(φ(φ(1,0)+φ(2)+1)) |
| ε0ωω2+ω = ωωε0+ω2+ω |
φ(φ(φ(1,0)+φ(2)+φ(1))) |
| ε0ωω2×2 = ωωε0+ω2×2 |
φ(φ(φ(1,0)+φ(2)+φ(2))) |
| ε0ωω3 = ωωε0+ω3 |
φ(φ(φ(1,0)+φ(3))) |
| ε0ωωω = ωωε0+ωω |
φ(φ(φ(1,0)+φ(φ(1)))) |
| ε0ωωω+1 = ωωε0+ωω+1 |
φ(φ(φ(1,0)+φ(φ(1))+1)) |
| ε0ωωω+ω = ωωε0+ωω+ω |
φ(φ(φ(1,0)+φ(φ(1))+φ(1))) |
| ε0ωωω+ω2 = ωωε0+ωω+ω2 |
φ(φ(φ(1,0)+φ(φ(1))+φ(2))) |
| ε0ωωω×2 = ωωε0+ωω×2 |
φ(φ(φ(1,0)+φ(φ(1))+φ(φ(1)))) |
| ε0ωωω+1 = ωωε0+ωω+1 |
φ(φ(φ(1,0)+φ(φ(1)+1))) |
| ε0ωωω+1+1 = ωωε0+ωω+1+1 |
φ(φ(φ(1,0)+φ(φ(1)+1)+1)) |
| ε0ωωω+1+ωω = ωωε0+ωω+1+ωω |
φ(φ(φ(1,0)+φ(φ(1)+1)+φ(φ(1)))) |
| ε0ωωω+1×2 = ωωε0+ωω+1×2 |
φ(φ(φ(1,0)+φ(φ(1)+1)+φ(φ(1)+1))) |
| ε0ωωω+2 = ωωε0+ωω+2 |
φ(φ(φ(1,0)+φ(φ(1)+2))) |
| ε0ωωω×2 = ωωε0+ωω×2 |
φ(φ(φ(1,0)+φ(φ(1)+φ(1)))) |
| ε0ωωω×3 = ωωε0+ωω×3 |
φ(φ(φ(1,0)+φ(φ(1)+φ(1)+φ(1)))) |
| ε0ωωω2 = ωωε0+ωω2 |
φ(φ(φ(1,0)+φ(φ(2)))) |
| ε0ωωω3 = ωωε0+ωω3 |
φ(φ(φ(1,0)+φ(φ(3)))) |
| ε0ωωωω = ωωε0+ωωω |
φ(φ(φ(1,0)+φ(φ(φ(1))))) |
| ε0ωωωω+1 = ωωε0+ωωω+1 |
φ(φ(φ(1,0)+φ(φ(φ(1)+1)))) |
| ε0ωωωω×2 = ωωε0+ωωω×2 |
φ(φ(φ(1,0)+φ(φ(φ(1)+φ(1))))) |
| ε0ωωωω2 = ωωε0+ωωω2 |
φ(φ(φ(1,0)+φ(φ(φ(2))))) |
| ε0ωωωω3 = ωωε0+ωωω3 |
φ(φ(φ(1,0)+φ(φ(φ(3))))) |
| ε0ωωωωω = ωωε0+ωωωω |
φ(φ(φ(1,0)+φ(φ(φ(φ(1)))))) |
| ε0ε0 = ωωε0×2 |
φ(φ(φ(1,0)+φ(1,0))) |
| ε0ε0+1 = ωωε0×2+1 |
φ(φ(φ(1,0)+φ(1,0)))+1 |
| ε0ε0+ε0 = ωωε0×2+ε0 |
φ(φ(φ(1,0)+φ(1,0)))+φ(1,0) |
| ε0ε0+ε0ω = ωωε0×2+ωωε0+1 |
φ(φ(φ(1,0)+φ(1,0)))+φ(φ(φ(1,0)+1)) |
| ε0ε0×2 = ωωε0×2×2 |
φ(φ(φ(1,0)+φ(1,0)))+φ(φ(φ(1,0)+φ(1,0))) |
| ε0ε0×ω = ωωε0×2+1 |
φ(φ(φ(1,0)+φ(1,0))+1) |
| ε0ε0+1 = ωωε0×2+ε0 |
φ(φ(φ(1,0)+φ(1,0))+φ(1,0)) |
| ε0ε0+ω = ωωε0×2+ωε0+1 |
φ(φ(φ(1,0)+φ(1,0))+φ(φ(1,0)+1)) |
| ε0ε0×2 = ωωε0×2×2 |
φ(φ(φ(1,0)+φ(1,0))+φ(φ(1,0)+φ(1,0))) |
| ε0ε0×3 = ωωε0×2×3 |
φ(φ(φ(1,0)+φ(1,0))+φ(φ(1,0)+φ(1,0))+φ(φ(1,0)+φ(1,0))) |
| ε0ε0×ω = ωωε0×2+1 |
φ(φ(φ(1,0)+φ(1,0)+1)) |
| ε0ε0×ωω = ωωε0×2+ω |
φ(φ(φ(1,0)+φ(1,0)+φ(1))) |
| ε0ε0×ωωω = ωωε0×2+ωω |
φ(φ(φ(1,0)+φ(1,0)+φ(φ(1)))) |
| ε0ε02 = ωωε0×3 |
φ(φ(φ(1,0)+φ(1,0)+φ(1,0))) |
| ε0ε03 = ωωε0×4 |
φ(φ(φ(1,0)+φ(1,0)+φ(1,0)+φ(1,0))) |
| ε0ε0ω = ωωωε0+1 |
φ(φ(φ(φ(1,0)+1))) |
| ε0ε0ω+1 = ωωωε0+1+ε0 |
φ(φ(φ(φ(1,0)+1)+φ(1,0))) |
| ε0ε0ω×2 = ωωωε0+1×2 |
φ(φ(φ(φ(1,0)+1)+φ(φ(1,0)+1))) |
| ε0ε0ω2 = ωωωε0+2 |
φ(φ(φ(φ(1,0)+2))) |
| ε0ε0ωω = ωωωε0+ω |
φ(φ(φ(φ(1,0)+φ(1)))) |
| ε0ε0ωω+1 = ωωωε0+ω+ε0 |
φ(φ(φ(φ(1,0)+φ(1))+φ(1,0))) |
| ε0ε0ωω×2 = ωωωε0+ω×2 |
φ(φ(φ(φ(1,0)+φ(1))+φ(φ(1,0)+φ(1)))) |
| ε0ε0ωω+1 = ωωωε0+ω+1 |
φ(φ(φ(φ(1,0)+φ(1)+1))) |
| ε0ε0ωω×2 = ωωωε0+ω×2 |
φ(φ(φ(φ(1,0)+φ(1)+φ(1)))) |
| ε0ε0ωω2 = ωωωε0+ω2 |
φ(φ(φ(φ(1,0)+φ(2)))) |
| ε0ε0ωωω = ωωωε0+ωω |
φ(φ(φ(φ(1,0)+φ(φ(1))))) |
| ε0ε0ε0 = ωωωε0×2 |
φ(φ(φ(φ(1,0)+φ(1,0)))) |
| ε0ε0ε0×2 = ωωωε0×2×2 |
φ(φ(φ(φ(1,0)+φ(1,0))+φ(φ(1,0)+φ(1,0)))) |
| ε0ε0ε0×ω = ωωωε0×2+1 |
φ(φ(φ(φ(1,0)+φ(1,0)+1))) |
| ε0ε0ε0×ωω = ωωωε0×2+ω |
φ(φ(φ(φ(1,0)+φ(1,0)+φ(1)))) |
| ε0ε0ε0×ωωω = ωωωε0×2+ωω |
φ(φ(φ(φ(1,0)+φ(1,0)+φ(φ(1))))) |
| ε0ε0ε02 = ωωωε0×3 |
φ(φ(φ(φ(1,0)+φ(1,0)+φ(1,0)))) |
| ε0ε0ε0ω = ωωωωε0+1 |
φ(φ(φ(φ(φ(1,0)+1)))) |
| ε0ε0ε0ω+1 = ωωωωε0+1+ε0 |
φ(φ(φ(φ(φ(1,0)+1))+φ(1,0))) |
| ε0ε0ε0ω+2 = ωωωωε0+1+ε0×2 |
φ(φ(φ(φ(φ(1,0)+1))+φ(1,0)+φ(1,0))) |
| ε0ε0ε0ω+ω = ωωωωε0+1+ωε0+1 |
φ(φ(φ(φ(φ(1,0)+1))+φ(φ(1,0)+1))) |
| ε0ε0ε0ω+ε0 = ωωωωε0+1+ωε0×2 |
φ(φ(φ(φ(φ(1,0)+1))+φ(φ(1,0)+φ(1,0)))) |
| ε0ε0ε0ω×2 = ωωωωε0+1×2 |
φ(φ(φ(φ(φ(1,0)+1))+φ(φ(φ(1,0)+1)))) |
| ε0ε0ε0ω×ω = ωωωωε0+1+1 |
φ(φ(φ(φ(φ(1,0)+1)+1))) |
| ε0ε0ε0ω+1 = ωωωωε0+1+ε0 |
φ(φ(φ(φ(φ(1,0)+1)+φ(1,0)))) |
| ε0ε0ε0ω+1×2 = ωωωωε0+1+ε0×2 |
φ(φ(φ(φ(φ(1,0)+1)+φ(1,0))+φ(φ(φ(1,0)+1)+φ(1,0)))) |
| ε0ε0ε0ω+1×ω = ωωωωε0+1+ε0+1 |
φ(φ(φ(φ(φ(1,0)+1)+φ(1,0)+1))) |
| ε0ε0ε0ω+2 = ωωωωε0+1+ε0×2 |
φ(φ(φ(φ(φ(1,0)+1)+φ(1,0)+φ(1,0)))) |
| ε0ε0ε0ω×2 = ωωωωε0+1×2 |
φ(φ(φ(φ(φ(1,0)+1)+φ(φ(1,0)+1)))) |
| ε0ε0ε0ω2 = ωωωωε0+2 |
φ(φ(φ(φ(φ(1,0)+2)))) |
| ε0ε0ε0ω3 = ωωωωε0+3 |
φ(φ(φ(φ(φ(1,0)+3)))) |
| ε0ε0ε0ωω = ωωωωε0+ω |
φ(φ(φ(φ(φ(1,0)+φ(1))))) |
| ε0ε0ε0ωωω = ωωωωε0+ωω |
φ(φ(φ(φ(φ(1,0)+φ(φ(1)))))) |
| ε0ε0ε0ε0 = ωωωωε0×2 |
φ(φ(φ(φ(φ(1,0)+φ(1,0))))) |
| ε0ε0ε0ε0×ω = ωωωωε0×2+1 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)))+1)) |
| ε0ε0ε0ε0+1 = ωωωωε0×2+ε0 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)))+φ(1,0))) |
| ε0ε0ε0ε0+ω = ωωωωε0×2+ωε0+1 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)))+φ(φ(1,0)+1))) |
| ε0ε0ε0ε0+ε0 = ωωωωε0×2+ωε0×2 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)))+φ(φ(1,0)+φ(1,0)))) |
| ε0ε0ε0ε0+ε0ω = ωωωωε0×2+ωωε0+1 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)))+φ(φ(φ(1,0)+1)))) |
| ε0ε0ε0ε0×2 = ωωωωε0×2×2 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)))+φ(φ(φ(1,0)+φ(1,0))))) |
| ε0ε0ε0ε0×ω = ωωωωε0×2+1 |
φ(φ(φ(φ(φ(1,0)+φ(1,0))+1))) |
| ε0ε0ε0ε0+1 = ωωωωε0×2+ε0 |
φ(φ(φ(φ(φ(1,0)+φ(1,0))+φ(1,0)))) |
| ε0ε0ε0ε0×2 = ωωωωε0×2×2 |
φ(φ(φ(φ(φ(1,0)+φ(1,0))+φ(φ(1,0)+φ(1,0))))) |
| ε0ε0ε0ε0×ω = ωωωωε0×2+1 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)+1)))) |
| ε0ε0ε0ε0×ωω = ωωωωε0×2+ω |
φ(φ(φ(φ(φ(1,0)+φ(1,0)+φ(1))))) |
| ε0ε0ε0ε02 = ωωωωε0×3 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)+φ(1,0))))) |
| ε0ε0ε0ε0ω = ωωωωωε0+1 |
φ(φ(φ(φ(φ(φ(1,0)+1))))) |
| ε0ε0ε0ε0ε0 = ωωωωωε0×2 |
φ(φ(φ(φ(φ(φ(1,0)+φ(1,0)))))) |
| ε0ε0ε0ε0ε0ω = ωωωωωωε0+1 |
φ(φ(φ(φ(φ(φ(φ(1,0)+1)))))) |
| ε1 = ε0ε0ε0ε0...= ωωω...ε0+1 = 1Ɛ1 |
φ(1,1) = φ(φ(φ(φ(φ(φ(...φ(1,0)+1...)))))) |
| ε1+1 |
φ(1,1)+1 |
| ε1+ω |
φ(1,1)+φ(1) |
| ε1+ωω |
φ(1,1)+φ(φ(1)) |
| ε1+ε0 |
φ(1,1)+φ(1,0) |
| ε1×2 |
φ(1,1)+φ(1,1) |
| ε1×ω = ωε1+1 |
φ(φ(1,1)+1) |
| ε1ω = ωωε1+1 |
φ(φ(φ(1,1)+1)) |
| ε1ωω = ωωε1+ω |
φ(φ(φ(1,1)+φ(1))) |
| ε1ε0 = ωωε1+ε0 |
φ(φ(φ(1,1)+φ(1,0))) |
| ε1ε1 = ωωε1×2 |
φ(φ(φ(1,1)+φ(1,1))) |
| ε1ε12 = ωωε1×3 |
φ(φ(φ(1,1)+φ(1,1)+φ(1,1))) |
| ε1ε1ω = ωωωε1+1 |
φ(φ(φ(φ(1,1)+1))) |
| ε1ε1ω+1 = ωωωε1+1+ε1 |
φ(φ(φ(φ(1,1)+1)+φ(1,1))) |
| ε1ε1ω×2 = ωωωε1+1×2 |
φ(φ(φ(φ(1,1)+1)+φ(φ(1,1)+1))) |
| ε1ε1ω2 = ωωωε1+2 |
φ(φ(φ(φ(1,1)+2))) |
| ε1ε1ωω = ωωωε1+ω |
φ(φ(φ(φ(1,1)+φ(1)))) |
| ε1ε1ε0 = ωωωε1+ε0 |
φ(φ(φ(φ(1,1)+φ(1,0)))) |
| ε1ε1ε0ω = ωωωε1+ωε0+1 |
φ(φ(φ(φ(1,1)+φ(φ(1,0)+1)))) |
| ε1ε1ε1 = ωωωε1×2 |
φ(φ(φ(φ(1,1)+φ(1,1)))) |
| ε1ε1ε1ω = ωωωωε1+1 |
φ(φ(φ(φ(φ(1,1)+1)))) |
| ε1ε1ε1ω×2 = ωωωωε1+1×2 |
φ(φ(φ(φ(φ(1,1)+1))+φ(φ(φ(1,1)+1)))) |
| ε1ε1ε1ω×ω = ωωωωε1+1+1 |
φ(φ(φ(φ(φ(1,1)+1)+1))) |
| ε1ε1ε1ω+1 = ωωωωε1+1+ε1 |
φ(φ(φ(φ(φ(1,1)+1)+φ(1,1)))) |
| ε1ε1ε1ω×2 = ωωωωε1+1×2 |
φ(φ(φ(φ(φ(1,1)+1)+φ(φ(1,1)+1)))) |
| ε1ε1ε1ω2 = ωωωωε1+2 |
φ(φ(φ(φ(φ(1,1)+2)))) |
| ε1ε1ε1ωω = ωωωωε1+ω |
φ(φ(φ(φ(φ(1,1)+φ(1))))) |
| ε1ε1ε1ε1 = ωωωωε1×2 |
φ(φ(φ(φ(φ(1,1)+φ(1,1))))) |
| ε1ε1ε1ε1ω = ωωωωωε1+1 |
φ(φ(φ(φ(φ(φ(1,1)+1))))) |
| ε1ε1ε1ε1ε1 = ωωωωωε1×2 |
φ(φ(φ(φ(φ(φ(1,1)+φ(1,1)))))) |
| ε1ε1ε1ε1ε1ω = ωωωωωωε1+1 |
φ(φ(φ(φ(φ(φ(φ(1,1)+1)))))) |
| ε2 = ε1ε1ε1ε1...= ωωω...ε1+1= 1Ɛ2 |
φ(1,2) = φ(φ(φ(φ(φ(φ(...φ(1,1)+1...)))))) |
| ε2×ω = ωε2+1 |
φ(φ(1,2)+1) |
| ε2ω = ωωε2+1 |
φ(φ(φ(1,2)+1)) |
| ε2ε2 = ωωε2×2 |
φ(φ(φ(1,2)+φ(1,2))) |
| ε2ε2ω = ωωωε2+1 |
φ(φ(φ(φ(1,2)+1))) |
| ε2ε2ε2 = ωωωε2×2 |
φ(φ(φ(φ(1,2)+φ(1,2)))) |
| ε2ε2ε2ω = ωωωωε2+1 |
φ(φ(φ(φ(φ(1,2)+1)))) |
| ε2ε2ε2ε2 = ωωωωε2×2 |
φ(φ(φ(φ(φ(1,2)+φ(1,2))))) |
| ε2ε2ε2ε2ω = ωωωωωε2+1 |
φ(φ(φ(φ(φ(φ(1,2)+1))))) |
| ε2ε2ε2ε2ε2 = ωωωωωε2×2 |
φ(φ(φ(φ(φ(φ(1,2)+φ(1,2)))))) |
| ε2ε2ε2ε2ε2ω = ωωωωωωε2+1 |
φ(φ(φ(φ(φ(φ(φ(1,2)+1)))))) |
| ε3 = ε2ε2ε2ε2...= ωωω...ε2+1= 1Ɛ3 |
φ(1,3) = φ(φ(φ(φ(φ(φ(...φ(1,2)+1...)))))) |
| ε4 = ε3ε3ε3ε3... = ωωωω...ε3+1 = 1Ɛ4 |
φ(1,4) = φ(φ(φ(φ(φ(φ(...φ(1,3)+1...)))))) |
| εω = 1Ɛω |
φ(1,ω) = φ(1,φ(1)) |
| εω+1 |
φ(1,φ(1))+1 |
| εω+ω |
φ(1,φ(1))+φ(1) |
| εω+ωω |
φ(1,φ(1))+φ(φ(1)) |
| εω+ε0 |
φ(1,φ(1))+φ(1,0) |
| εω+ε1 |
φ(1,φ(1))+φ(1,1) |
| εω×2 |
φ(1,φ(1))+φ(1,φ(1)) |
| εω×2+1 |
φ(1,φ(1))+φ(1,φ(1))+1 |
| εω×2+ε0 |
φ(1,φ(1))+φ(1,φ(1))+φ(1,0) |
| εω×3 |
φ(1,φ(1))+φ(1,φ(1))+φ(1,φ(1)) |
| εω×ω = ωεω+1 |
φ(φ(1,φ(1))+1) = φ(1,φ(1))+φ(1,φ(1))+φ(1,φ(1))+... |
| εω×ωω = ωεω+ω |
φ(φ(1,φ(1))+φ(1)) |
| εω×ωωω = ωεω+ωω |
φ(φ(1,φ(1))+φ(φ(1))) |
| εω×ε0 = ωεω+ε0 |
φ(φ(1,φ(1))+φ(1,0)) |
| εω2 = ωεω×2 |
φ(φ(1,φ(1))+φ(1,φ(1))) |
| εωω = ωωεω+1 |
φ(φ(φ(1,φ(1))+1)) |
| εωωω = ωωεω+ω |
φ(φ(φ(1,φ(1))+φ(1))) |
| εωε0 = ωωεω+ε0 |
φ(φ(φ(1,φ(1))+φ(1,0))) |
| εωε1 = ωωεω+ε1 |
φ(φ(φ(1,φ(1))+φ(1,1))) |
| εωεω = ωωεω×2 |
φ(φ(φ(1,φ(1))+φ(1,φ(1)))) |
| εωεω×ω = ωωεω×2+1 |
φ(φ(φ(1,φ(1))+φ(1,φ(1))+1)) |
| εωεω×ε0 = ωωεω×2+ε0 |
φ(φ(φ(1,φ(1))+φ(1,φ(1))+φ(1,0))) |
| εωεω2 = ωωεω×3 |
φ(φ(φ(1,φ(1))+φ(1,φ(1))+φ(1,φ(1)))) |
| εωεωω = ωωωεω+1 |
φ(φ(φ(φ(1,φ(1))+1))) |
| εωεωωω = ωωωεω+ω |
φ(φ(φ(φ(1,φ(1))+φ(1)))) |
| εωεωωωω = ωωωεω+ωω |
φ(φ(φ(φ(1,φ(1))+φ(φ(1))))) |
| εωεωε0 = ωωωεω+ε0 |
φ(φ(φ(φ(1,φ(1))+φ(1,0)))) |
| εωεωεω = ωωωεω×2 |
φ(φ(φ(φ(1,φ(1))+φ(1,φ(1))))) |
| εωεωεωω = ωωωωεω+1 |
φ(φ(φ(φ(φ(1,φ(1))+1)))) |
| εωεωεωωω = ωωωωεω+ω |
φ(φ(φ(φ(φ(1,φ(1))+φ(1))))) |
| εωεωεωεω = ωωωωεω×2 |
φ(φ(φ(φ(φ(1,φ(1))+φ(1,φ(1)))))) |
| εωεωεωεωω = ωωωωωεω+1 |
φ(φ(φ(φ(φ(φ(1,φ(1))+1))))) |
| εωεωεωεωωω = ωωωωωεω+ω |
φ(φ(φ(φ(φ(φ(1,φ(1))+φ(1)))))) |
| εωεωεωεωεω = ωωωωωεω×2 |
φ(φ(φ(φ(φ(φ(1,φ(1))+φ(1,φ(1))))))) |
| εωεωεωεωεωω = ωωωωωωεω+1 |
φ(φ(φ(φ(φ(φ(φ(1,φ(1))+1)))))) |
| εωεωεωεωεωωω = ωωωωωωεω+ω |
φ(φ(φ(φ(φ(φ(φ(1,φ(1))+φ(1))))))) |
| εωεωεωεωεωεω = ωωωωωωεω×2 |
φ(φ(φ(φ(φ(φ(φ(1,φ(1))+φ(1,φ(1)))))))) |
| εω+1 = εωεωεωεω...= ωωω...εω+1 |
φ(1,φ(1)+1) = φ(φ(φ(φ(...φ(1,φ(1))+1...)))) |
| εω+2 = εω+1εω+1εω+1εω+1...= ωωω...εω+1+1 |
φ(1,φ(1)+2) = φ(φ(φ(φ(...φ(1,φ(1)+1)+1...)))) |
| εω×2 |
φ(1,φ(1)+φ(1)) |
| εω2 |
φ(1,φ(2)) |
| εωω |
φ(1,φ(φ(1))) |
| εωωω |
φ(1,φ(φ(φ(1)))) |
| εωωωω |
φ(1,φ(φ(φ(φ(1))))) |
| εε0 = εωωωω... |
φ(1,ε0) = φ(1,φ(1,0)) = φ(1,φ(φ(φ(φ(φ(...)))))) |
| εε0+1 |
φ(1,φ(1,0))+1 |
| εε0×2 |
φ(1,φ(1,0))+φ(1,φ(1,0)) |
| εε0×ω = ωεε0+1 |
φ(φ(1,φ(1,0))+1) |
| εε02 = ωεε0×2 |
φ(φ(1,φ(1,0))+φ(1,φ(1,0))) |
| εε0ω = ωωεε0+1 |
φ(φ(φ(1,φ(1,0))+1)) |
| εε0εε0 = ωωεε0×2 |
φ(φ(φ(1,φ(1,0))+φ(1,φ(1,0)))) |
| εε0+1 = ωωω...εε0+1 |
φ(1,φ(1,0)+1) |
| εε0+ω |
φ(1,φ(1,0)+φ(1)) |
| εε0+ωω |
φ(1,φ(1,0)+φ(φ(1))) |
| εε0+ωωω |
φ(1,φ(1,0)+φ(φ(φ(1)))) |
| εε0×2 |
φ(1,φ(1,0)+φ(1,0)) |
| εε0×3 |
φ(1,φ(1,0)+φ(1,0)+φ(1,0)) |
| εε0×ω = εωε0+1 |
φ(1,φ(φ(1,0)+1)) |
| εε0×ω+εε0 |
φ(1,φ(φ(1,0)+1))+φ(1,φ(1,0)+1) |
| εε0×ω×2 |
φ(1,φ(φ(1,0)+1))+φ(1,φ(φ(1,0)+1)) |
| εε0×ω×ω = ωεε0×ω+1 |
φ(φ(1,φ(φ(1,0)+1))+1) |
| εε0×ω+1 = εωε0+1+1 = ωωω...εε0×ω+1 |
φ(1,φ(φ(1,0)+1)+1) |
| εε0×ω×2 = εωε0+1×2 |
φ(1,φ(φ(1,0)+1)+φ(φ(1,0)+1)) |
| εε0×ω2 = εωε0+2 |
φ(1,φ(φ(1,0)+2)) |
| εε0×ωω = εωε0+ω |
φ(1,φ(φ(1,0)+φ(1))) |
| εε02 = εωε0×2 |
φ(1,φ(φ(1,0)+φ(1,0))) |
| εε0ω = εωωε0+1 |
φ(1,φ(φ(φ(1,0)+1))) |
| εε0ω2 = εωωε0+2 |
φ(1,φ(φ(φ(1,0)+2))) |
| εε0ωω = εωωε0+ω |
φ(1,φ(φ(φ(1,0)+φ(1)))) |
| εε0ε0 = εωωε0×2 |
φ(1,φ(φ(φ(1,0)+φ(1,0)))) |
| εε0ε0ω = εωωωε0+1 |
φ(1,φ(φ(φ(φ(1,0)+1)))) |
| εε0ε0ωω = εωωωε0+ω |
φ(1,φ(φ(φ(φ(1,0)+φ(1))))) |
| εε0ε0ε0 = εωωωε0×2 |
φ(1,φ(φ(φ(φ(1,0)+φ(1,0))))) |
| εε0ε0ε0ω = εωωωωε0+1 |
φ(1,φ(φ(φ(φ(1,0)+1)))) |
| εε0ε0ε0ωω = εωωωωε0+ω |
φ(1,φ(φ(φ(φ(1,0)+φ(1))))) |
| εε0ε0ε0ε0 = εωωωωε0×2 |
φ(1,φ(φ(φ(φ(1,0)+φ(1,0))))) |
| εε1 = εε0ε0ε0ε0... = εωωω...ε0+1 |
φ(1,φ(1,1)) = φ(1,φ(φ(φ(φ(...φ(1,0)+1...))))) |
| εε1+1 |
φ(1,φ(1,1))+1 |
| εε1×2 |
φ(1,φ(1,1))+φ(1,φ(1,1)) |
| εε1×ω = ωεε1+1 |
φ(φ(1,φ(1,1))+1) |
| εε12 = ωεε1×2 |
φ(φ(1,φ(1,1))+φ(1,φ(1,1))) |
| εε1ω = ωωεε1+1 |
φ(φ(φ(1,φ(1,1))+1)) |
| εε1+1 = ωωω...εε1+1 |
φ(1,φ(1,1)+1) |
| εε1+ε0 |
φ(1,φ(1,1)+φ(1,0)) |
| εε1×2 |
φ(1,φ(1,1)+φ(1,1)) |
| εε1×ω = εωε1+1 |
φ(1,φ(φ(1,1)+1)) |
| εε1×ωω = εωε1+ω |
φ(1,φ(φ(1,1)+φ(1))) |
| εε12 = εωε1×2 |
φ(1,φ(φ(1,1)+φ(1,1))) |
| εε1ω = εωωε1+1 |
φ(1,φ(φ(φ(1,1)+1))) |
| εε1ωω = εωωε1+ω |
φ(1,φ(φ(φ(1,1)+φ(1)))) |
| εε1ε1 = εωωε1×2 |
φ(1,φ(φ(φ(1,1)+φ(1,1)))) |
| εε2 = εε1ε1ε1ε1... = εωωω...ε1+1 |
φ(1,φ(1,2)) = φ(1,φ(φ(φ(φ(...φ(1,1)+1...))))) |
| εε3 = εε2ε2ε2ε2... = εωωω...ε2+1 |
φ(1,φ(1,3)) = φ(1,φ(φ(φ(φ(...φ(1,2)+1...))))) |
| εεω |
φ(1,φ(1,φ(1))) |
| εεω+1 |
φ(1,φ(1,φ(1))+1) |
| εεω×2 |
φ(1,φ(1,φ(1))+φ(1,φ(1))) |
| εεω+1 |
φ(1,φ(1,φ(1)+1)) |
| εεω+2 |
φ(1,φ(1,φ(1)+2)) |
| εεω×2 |
φ(1,φ(1,φ(1)+φ(1))) |
| εεω2 |
φ(1,φ(1,φ(2))) |
| εεωω |
φ(1,φ(1,φ(φ(1)))) |
| εεε0 |
φ(1,φ(1,φ(1,0))) |
| εεε0+1 |
φ(1,φ(1,φ(1,0))+1) |
| εεε0+ε0 |
φ(1,φ(1,φ(1,0))+φ(1,0)) |
| εεε0×2 |
φ(1,φ(1,φ(1,0))+φ(1,φ(1,0))) |
| ε(εε0)ω |
φ(1,φ(φ(1,φ(1,0))+1)) |
| εεε0+1 |
φ(1,φ(1,φ(1,0)+1)) |
| εεε0×2 |
φ(1,φ(1,φ(1,0)+φ(1,0))) |
| εεε1 |
φ(1,φ(1,φ(1,1))) |
| εεεω |
φ(1,φ(1,φ(1,φ(1)))) |
| εεεε0 |
φ(1,φ(1,φ(1,φ(1,0)))) |
| εεεεω |
φ(1,φ(1,φ(1,φ(1,φ(1))))) |
| εεεεε0 |
φ(1,φ(1,φ(1,φ(1,φ(1,0))))) |
| ζ0 = εεεε... = 2Ɛ0 |
φ(2,0) = φ(1,φ(1,φ(1,φ(1,φ(1,...)))) |
| ζ0+1 |
φ(2,0)+1 = φ(2,0)+φ(0) |
| ζ0+ω |
φ(2,0)+φ(1) |
| ζ0+ε0 |
φ(2,0)+φ(1,0) |
| ζ0×2 |
φ(2,0)+φ(2,0) |
| ζ0×ω = ωζ0+1 |
φ(φ(2,0)+1) |
| ζ0×ωω = ωζ0+ω |
φ(φ(2,0)+φ(1)) |
| ζ0×ε0 = ωζ0+ε0 |
φ(φ(2,0)+φ(1,0)) |
| ζ02 = ωζ0×2 |
φ(φ(2,0)+φ(2,0)) |
| ζ0ω = ωωζ0+1 |
φ(φ(φ(2,0)+1)) |
| ζ0ωω = ωωζ0+ω |
φ(φ(φ(2,0)+φ(1))) |
| ζ0ε0 = ωωζ0+ε0 |
φ(φ(φ(2,0)+φ(1,0))) |
| ζ0ζ0 = ωωζ0×2 |
φ(φ(φ(2,0)+φ(2,0))) |
| ζ0ζ0ω = ωωωζ0+1 |
φ(φ(φ(φ(2,0)+1))) |
| ζ0ζ0ζ0 = ωωωζ0×2 |
φ(φ(φ(φ(2,0)+φ(2,0)))) |
| ζ0ζ0ζ0ω = ωωωωζ0+1 |
φ(φ(φ(φ(φ(2,0)+1)))) |
| ζ0ζ0ζ0ζ0 = ωωωωζ0×2 |
φ(φ(φ(φ(φ(2,0)+φ(2,0))))) |
| ζ0ζ0ζ0ζ0ω = ωωωωωζ0+1 |
φ(φ(φ(φ(φ(φ(2,0)+1))))) |
| ζ0ζ0ζ0ζ0ζ0 = ωωωωωζ0×2 |
φ(φ(φ(φ(φ(φ(2,0)+φ(2,0)))))) |
| ζ0ζ0ζ0ζ0ζ0ω = ωωωωωωζ0+1 |
φ(φ(φ(φ(φ(φ(φ(2,0)+1)))))) |
| εζ0+1 = ζ0ζ0ζ0ζ0...= ωωω...ζ0+1 |
φ(1,φ(2,0)+1) = φ(φ(φ(φ(φ(φ(...φ(2,0)+1...)))))) |
| εζ0+1+1 |
φ(1,φ(2,0)+1)+1 |
| εζ0+1+ζ0 |
φ(1,φ(2,0)+1)+φ(2,0) |
| εζ0+1×2 |
φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1) |
| εζ0+1×2+1 |
φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)+1 |
| εζ0+1×2+ζ0 |
φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)+φ(2,0) |
| εζ0+1×3 |
φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1) |
| εζ0+1×ω = ωεζ0+1+1 |
φ(φ(1,φ(2,0)+1)+1) |
| εζ0+1×ζ0 = ωεζ0+1+ζ0 |
φ(φ(1,φ(2,0)+1)+φ(2,0)) |
| εζ0+12 = ωεζ0+1×2 |
φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)) |
| εζ0+1ω = ωωεζ0+1+1 |
φ(φ(φ(1,φ(2,0)+1)+1)) |
| εζ0+1ζ0 = ωωεζ0+1+ζ0 |
φ(φ(φ(1,φ(2,0)+1)+φ(2,0))) |
| εζ0+1εζ0+1 = ωωεζ0+1×2 |
φ(φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1))) |
| εζ0+1εζ0+1×ω = ωωεζ0+1×2+1 |
φ(φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)+1)) |
| εζ0+1εζ0+1×ζ0 = ωωεζ0+1×2+ζ0 |
φ(φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)+φ(2,0))) |
| εζ0+1εζ0+12 = ωωεζ0+1×3 |
φ(φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1))) |
| εζ0+1εζ0+1ω = ωωωεζ0+1+1 |
φ(φ(φ(φ(1,φ(2,0)+1)+1))) |
| εζ0+1εζ0+1εζ0+1 = ωωωεζ0+1×2 |
φ(φ(φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)))) |
| εζ0+1εζ0+1εζ0+1ω = ωωωωεζ0+1+1 |
φ(φ(φ(φ(φ(1,φ(2,0)+1)+1)))) |
| εζ0+2 = εζ0+1εζ0+1εζ0+1... = ωωω...εζ0+1+1 |
φ(1,φ(2,0)+2) = φ(φ(φ(φ(...φ(1,φ(2,0)+1)+1...)))) |
| εζ0+ω |
φ(1,φ(2,0)+φ(1)) |
| εζ0+ωω |
φ(1,φ(2,0)+φ(φ(1))) |
| εζ0+ε0 |
φ(1,φ(2,0)+φ(1,0)) |
| εζ0+ε1 |
φ(1,φ(2,0)+φ(1,1)) |
| εζ0+εε0 |
φ(1,φ(2,0)+φ(1,φ(1,0))) |
| εζ0×2 |
φ(1,φ(2,0)+φ(2,0)) |
| εζ0×2+1 = εζ0×2εζ0×2εζ0×2... = ωωω...εζ0×2+1 |
φ(1,φ(2,0)+φ(2,0)+1) = φ(φ(φ(φ(...φ(1,φ(2,0)+φ(2,0))+1...)))) |
| εζ0×3 |
φ(1,φ(2,0)+φ(2,0)+φ(2,0)) |
| εζ0×ω = εωζ0+1 |
φ(1,φ(φ(2,0)+1)) |
| εζ02 = εωζ0×2 |
φ(1,φ(φ(2,0)+φ(2,0))) |
| εζ0ω = εωωζ0+1 |
φ(1,φ(φ(φ(2,0)+1))) |
| εζ0ζ0 = εωωζ0×2 |
φ(1,φ(φ(φ(2,0)+φ(2,0)))) |
| εζ0ζ0ω = εωωωζ0+1 |
φ(1,φ(φ(φ(φ(2,0)+1)))) |
| εζ0ζ0ζ0 = εωωωζ0×2 |
φ(1,φ(φ(φ(φ(2,0)+φ(2,0))))) |
| εζ0ζ0ζ0ω = εωωωωζ0+1 |
φ(1,φ(φ(φ(φ(φ(2,0)+1))))) |
| εζ0ζ0ζ0ζ0 = εωωωωζ0×2 |
φ(1,φ(φ(φ(φ(φ(2,0)+φ(2,0)))))) |
| εεζ0+1 = εζ0ζ0ζ0ζ0... = εωωω...ζ0+1 |
φ(1,φ(1,φ(2,0)+1)) = φ(1,φ(φ(φ(φ(φ(...φ(2,0)+1...)))))) |
| εεζ0+1+1 = εεζ0+1εεζ0+1... |
φ(1,φ(1,φ(2,0)+1)+1) = φ(φ(φ(φ(...φ(1,φ(1,φ(2,0)+1))+1...)))) |
| εεζ0+1×2 |
φ(1,φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)) |
| εεζ0+1×ω = εωεζ0+1+1 |
φ(1,φ(φ(1,φ(2,0)+1)+1)) |
| ε(εζ0+1)2 = εωεζ0+1×2 |
φ(1,φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1))) |
| ε(εζ0+1)ω = εωωεζ0+1+1 |
φ(1,φ(φ(φ(1,φ(2,0)+1)+1))) |
| εεζ0+2 = ε(εζ0+1εζ0+1εζ0+1...) = εωωω...εζ0+1+1 |
φ(1,φ(1,φ(2,0)+2)) = φ(1,φ(φ(φ(φ(...φ(1,φ(2,0)+1)+1...))))) |
| εεζ0+ω |
φ(1,φ(1,φ(2,0)+φ(1))) |
| εεζ0+ε0 |
φ(1,φ(1,φ(2,0)+φ(1,0))) |
| εεζ0×2 |
φ(1,φ(1,φ(2,0)+φ(2,0))) |
| εεζ0×3 |
φ(1,φ(1,φ(2,0)+φ(2,0)+φ(2,0))) |
| εεζ0×ω = εεωζ0+1 |
φ(1,φ(1,φ(φ(2,0)+1))) |
| εεζ02 = εεωζ0×2 |
φ(1,φ(1,φ(φ(2,0)+φ(2,0)))) |
| εεζ0ω = εεωωζ0+1 |
φ(1,φ(1,φ(φ(φ(2,0)+1)))) |
| εεζ0ζ0 = εεωωζ0×2 |
φ(1,φ(1,φ(φ(φ(2,0)+φ(2,0))))) |
| εεεζ0+1 = εεζ0ζ0ζ0ζ0... = εεωωω...ζ0+1 |
φ(1,φ(1,φ(1,φ(2,0)+1))) = φ(1,φ(1,φ(φ(φ(φ(...φ(2,0)+1...)))))) |
| εεεζ0+2 = εε(εζ0+1εζ0+1εζ0+1...) = εεωωω...εζ0+1+1 |
φ(1,φ(1,φ(1,φ(2,0)+2))) = φ(1,φ(1,φ(φ(φ(φ(...φ(1,φ(2,0)+1)+1...)))))) |
| εεεζ0+ω |
φ(1,φ(1,φ(1,φ(2,0)+φ(1)))) |
| εεεζ0×2 |
φ(1,φ(1,φ(1,φ(2,0)+φ(2,0)))) |
| ζ1 = εεε...ζ0+1 = 2Ɛ1 |
φ(2,1) = φ(1,φ(1,φ(1,φ(1,...φ(2,0)+1...)))) |
| εζ1+1= ζ1ζ1ζ1ζ1...= ωωω...ζ1+1 |
φ(1,φ(2,1)+1) = φ(φ(φ(φ(φ(φ(...φ(2,1)+1...)))))) |
| εζ1+ω |
φ(1,φ(2,1)+φ(1)) |
| εζ1+ζ0 |
φ(1,φ(2,1)+φ(2,0)) |
| εζ1×2 |
φ(1,φ(2,1)+φ(2,1)) |
| εζ1×ω = εωζ1+1 |
φ(1,φ(φ(2,1)+1)) |
| εζ12 = εωζ1×2 |
φ(1,φ(φ(2,1)+φ(2,1))) |
| εζ1ω = εωωζ1+1 |
φ(1,φ(φ(φ(2,1)+1))) |
| εζ1ζ1 = εωωζ1×2 |
φ(1,φ(φ(φ(2,1)+φ(2,1)))) |
| εεζ1+1 = εζ1ζ1ζ1ζ1... = εωωω...ζ1+1 |
φ(1,φ(1,φ(2,1)+1)) = φ(1,φ(φ(φ(φ(φ(...φ(2,1)+1...)))))) |
| εεζ1+ω |
φ(1,φ(1,φ(2,1)+φ(1))) |
| εεζ1×2 |
φ(1,φ(1,φ(2,1)+φ(2,1))) |
| εεεζ1+1 = εεζ1ζ1ζ1ζ1... = εεωωω...ζ1+1 |
φ(1,φ(1,φ(1,φ(2,1)+1))) = φ(1,φ(1,φ(φ(φ(φ(...φ(2,1)+1...)))))) |
| εεεζ1×2 |
φ(1,φ(1,φ(1,φ(2,1)+(2,1)))) |
| ζ2 = εεε...ζ1+1= 2Ɛ2 |
φ(2,2) = φ(1,φ(1,φ(1,φ(1,...φ(2,1)+1...)))) |
| ζ3 = εεε...ζ2+1= 2Ɛ3 |
φ(2,3) = φ(1,φ(1,φ(1,φ(1,...φ(2,2)+1...)))) |
| ζω = 2Ɛω |
φ(2,ω) = φ(2,φ(1)) |
| ζωω |
φ(2,φ(φ(1))) |
| ζε0 = ζωωωω... |
φ(2,φ(1,0)) = φ(2,φ(φ(φ(φ(...))))) |
| ζζ0 = ζεεε... |
φ(2,φ(2,0)) = φ(2,φ(1,φ(1,φ(1,φ(1,...))))) |
| εζζ0+1 = ζζ0ζζ0ζζ0... = ωωω...ζζ0+1 |
φ(1,φ(2,φ(2,0))+1) = φ(φ(φ(φ(...φ(2,φ(2,0))+1...)))) |
| ζζ0+1 = εε...ζζ0+1 |
φ(2,φ(2,0)+1) = φ(1,φ(1,φ(1,φ(1,...φ(2,φ(2,0))+1...)))) |
| ζζ0×2 |
φ(2,φ(2,0)+φ(2,0)) |
| ζζ0×ω = ζωζ0+1 |
φ(2,φ(φ(2,0)+1)) |
| ζζ02 = ζωζ0×2 |
φ(2,φ(φ(2,0)+φ(2,0))) |
| ζζ0ω = ζωωζ0+1 |
φ(2,φ(φ(φ(2,0)+1))) |
| ζζ0ζ0 = ζωωζ0×2 |
φ(2,φ(φ(φ(2,0)+φ(2,0)))) |
| ζεζ0+1 = ζζ0ζ0ζ0ζ0... = ζωωω...ζ0+1 |
φ(2,φ(1,φ(2,0)+1)) = φ(2,φ(φ(φ(φ(...φ(2,0)+1...))))) |
| ζεζ0+2 = ζ(εζ0+1εζ0+1εζ0+1...) = ζωωω...εζ0+1+1 |
φ(2,φ(1,φ(2,0)+2)) = φ(2,φ(φ(φ(φ(...φ(1,φ(2,0)+1)+1...))))) |
| ζεζ0×2 |
φ(2,φ(1,φ(2,0)+φ(2,0))) |
| ζεεζ0+1 = ζεζ0ζ0ζ0ζ0... = ζεωωω...ζ0+1 |
φ(2,φ(1,φ(1,φ(2,0)+1))) = φ(2,φ(1,φ(φ(φ(φ(...φ(2,0)+1...)))))) |
| ζεεζ0×2 |
φ(2,φ(1,φ(1,φ(2,0)+φ(2,0)))) |
| ζζ1 = ζεε...ζ0+1 |
φ(2,φ(2,1)) = φ(2,φ(1,φ(1,φ(1,φ(1,...φ(2,0)+1...))))) |
| ζζ2 = ζεε...ζ1+1 |
φ(2,φ(2,2)) = φ(2,φ(1,φ(1,φ(1,φ(1,...φ(2,1)+1...))))) |
| ζζω |
φ(2,φ(2,φ(1))) |
| ζζε0 = ζζωωωω... |
φ(2,φ(2,φ(1,0))) = φ(2,φ(2,φ(φ(φ(φ(...)))))) |
| ζζζ0 = ζζεεε... |
φ(2,φ(2,φ(2,0))) = φ(2,φ(2,φ(1,φ(1,φ(1,φ(1,...)))))) |
| ζζζ0+1 = εε...ζζζ0+1 |
φ(2,φ(2,φ(2,0))+1) = φ(1,φ(1,φ(1,φ(1,...φ(2,φ(2,φ(2,0)))+1...)))) |
| ζζζ0×2 |
φ(2,φ(2,φ(2,0))+φ(2,φ(2,0))) |
| ζζζ0+1 = ζεε...ζζ0+1 |
φ(2,φ(2,φ(2,0)+1)) = φ(2,φ(1,φ(1,φ(1,φ(1,...φ(2,φ(2,0))+1...))))) |
| ζζζ0×2 |
φ(2,φ(2,φ(2,0)+φ(2,0))) |
| ζζζ1 = ζζεε...ζ0+1 |
φ(2,φ(2,φ(2,1))) = φ(2,φ(2,φ(1,φ(1,φ(1,φ(1,...φ(2,0)+1...)))))) |
| ζζζω |
φ(2,φ(2,φ(2,φ(1)))) |
| ζζζζ0 = ζζζεεε... |
φ(2,φ(2,φ(2,φ(2,0)))) = φ(2,φ(2,φ(2,φ(1,φ(1,φ(1,φ(1,...))))))) |
| ζζζζω |
φ(2,φ(2,φ(2,φ(2,φ(1))))) |
| η0 = ζζζζ... = 3Ɛ0 |
φ(3,0) = φ(2,φ(2,φ(2,φ(2,φ(2,...)))) |
| η0+1 |
φ(3,0)+1 = φ(3,0)+φ(0) |
| η0+ω |
φ(3,0)+φ(1) |
| η0×2 |
φ(3,0)+φ(3,0) |
| η0×ω = ωη0+1 |
φ(φ(3,0)+1) |
| η02 = ωη0×2 |
φ(φ(3,0)+φ(3,0)) |
| η0ω = ωωη0+1 |
φ(φ(φ(3,0)+1)) |
| η0η0 = ωωη0×2 |
φ(φ(φ(3,0)+φ(3,0))) |
| η0η0ω = ωωωη0+1 |
φ(φ(φ(φ(3,0)+1))) |
| η0η0η0 = ωωωη0×2 |
φ(φ(φ(φ(3,0)+φ(3,0)))) |
| η0η0η0ω = ωωωωη0+1 |
φ(φ(φ(φ(φ(3,0)+1)))) |
| η0η0η0η0 = ωωωωη0×2 |
φ(φ(φ(φ(φ(3,0)+φ(3,0))))) |
| η0η0η0η0ω = ωωωωωη0+1 |
φ(φ(φ(φ(φ(φ(3,0)+1))))) |
| εη0+1 = η0η0η0η0... = ωωω...η0+1 |
φ(1,φ(3,0)+1) = φ(φ(φ(φ(φ(φ(...φ(3,0)+1...)))))) |
| εη0+2 = εη0+1εη0+1εη0+1... = ωωω...εη0+1+1 |
φ(1,φ(3,0)+2) = φ(φ(φ(φ(φ(φ(...φ(1,φ(3,0)+1)+1...)))))) |
| εη0+ω |
φ(1,φ(3,0)+φ(1)) |
| εη0+ε0 |
φ(1,φ(3,0)+φ(1,0)) |
| εη0+ζ0 |
φ(1,φ(3,0)+φ(2,0)) |
| εη0×2 |
φ(1,φ(3,0)+φ(3,0)) |
| εεη0+1 = εη0η0η0η0... = εωωω...η0+1 |
φ(1,φ(1,φ(3,0)+1)) = φ(1,φ(φ(φ(φ(φ(...φ(3,0)+1...)))))) |
| εεη0×2 |
φ(1,φ(1,φ(3,0)+φ(3,0))) |
| εεεη0+1 = εεη0η0η0η0... = εεωωω...η0+1 |
φ(1,φ(1,φ(1,φ(3,0)+1))) = φ(1,φ(1,φ(φ(φ(φ(...φ(3,0)+1...)))))) |
| ζη0+1 = εεε...η0+1 |
φ(2,φ(3,0)+1) = φ(1,φ(1,φ(1,φ(1,...φ(3,0)+1...)))) |
| εζη0+1+1 = ζη0+1ζη0+1ζη0+1... = ωωω...ζη0+1+1 |
φ(1,φ(2,φ(3,0)+1)+1) = φ(φ(φ(φ(φ(...φ(2,φ(3,0)+1)+1...)))))) |
| ζη0+2 = εεε...εη0+1 |
φ(2,φ(3,0)+2) = φ(1,φ(1,φ(1,φ(1,...φ(2,φ(3,0)+1)+1...)))) |
| ζη0+ω |
φ(2,φ(3,0)+φ(1)) |
| ζη0+ε0 |
φ(2,φ(3,0)+φ(1,0)) |
| ζη0+ζ0 |
φ(2,φ(3,0)+φ(2,0)) |
| ζη0×2 |
φ(2,φ(3,0)+φ(3,0)) |
| ζεη0+1= ζη0η0η0η0... = ζωωω...η0+1 |
φ(2,φ(1,φ(3,0)+1)) = φ(2,φ(φ(φ(φ(...φ(3,0)+1...))))) |
| ζζη0+1 = ζεε...η0+1 |
φ(2,φ(2,φ(3,0)+1)) = φ(2,φ(1,φ(1,φ(1,φ(1,...φ(3,0)+1...))))) |
| ζζη0×2 |
φ(2,φ(2,φ(3,0)+φ(3,0))) |
| ζζζη0+1 = ζζεε...η0+1 |
φ(2,φ(2,φ(2,φ(3,0)+1))) = φ(2,φ(2,φ(1,φ(1,φ(1,φ(1,...φ(3,0)+1...)))))) |
| η1 = ζζζ...η0+1= 3Ɛ1 |
φ(3,1) = φ(2,φ(2,φ(2,φ(2,...φ(3,0)+1...)))) |
| η2 = ζζζ...η1+1 = 3Ɛ2 |
φ(3,2) = φ(2,φ(2,φ(2,φ(2,...φ(3,1)+1...)))) |
| ηω = 3Ɛω |
φ(3,ω) = φ(3,φ(1)) |
| ηωω |
φ(3,φ(φ(1))) |
| ηε0 = ηωωωω... |
φ(3,φ(1,0)) = φ(3,φ(φ(φ(φ(...))))) |
| ηζ0 = ηεεε... |
φ(3,φ(2,0)) = φ(3,φ(1,φ(1,φ(1,φ(1,...))))) |
| ηη0 = ηζζζ... |
φ(3,φ(3,0)) = φ(3,φ(2,φ(2,φ(2,φ(2,...))))) |
| ηη1 = ηζζ...η0+1 |
φ(3,φ(3,1)) = φ(3,φ(2,φ(2,φ(2,φ(2,...φ(3,0)+1...))))) |
| ηηη0 = ηηζζζ... |
φ(3,φ(3,φ(3,0))) = φ(3,φ(3,φ(2,φ(2,φ(2,φ(2,...)))))) |
| ηηηη0 = ηηηζζζ... |
φ(3,φ(3,φ(3,φ(3,0)))) = φ(3,φ(3,φ(3,φ(2,φ(2,φ(2,φ(2,...))))))) |
| 4Ɛ0 = ηηηη... |
φ(4,0) = φ(3,φ(3,φ(3,φ(3,φ(3,...)))) |
| 5Ɛ0 = 4Ɛ4Ɛ4Ɛ4Ɛ... |
φ(5,0) = φ(4,φ(4,φ(4,φ(4,φ(4,...)))) |
| ωƐ0 |
φ(ω,0) = φ(φ(1),0) |
| ωƐ0+1 |
φ(ω,0)+1 |
| ωƐ0+ω |
φ(ω,0)+φ(1) |
| ωƐ0+ε0 |
φ(ω,0)+φ(1,0) |
| ωƐ0+ζ0 |
φ(ω,0)+φ(2,0) |
| ωƐ0+η0 |
φ(ω,0)+φ(3,0) |
| ωƐ0×2 |
φ(ω,0)+φ(ω,0) |
| 0ƐωƐ0+1 = ωωƐ0+1 = ωƐ0×ω |
φ(φ(ω,0)+1) = ωφ(ω,0)+1 |
| 0Ɛ0ƐωƐ0+1 = ωωωƐ0+1 = ωƐ0ω |
φ(φ(φ(ω,0)+1)) = ωωφ(ω,0)+1 |
| 1ƐωƐ0+1 = εωƐ0+1 |
φ(1,φ(ω,0)+1) = εφ(ω,0)+1 |
| 1Ɛ1ƐωƐ0+1 = εεωƐ0+1 |
φ(1,φ(1,φ(ω,0)+1)) = εεφ(ω,0)+1 |
| 2ƐωƐ0+1 = ζωƐ0+1 |
φ(2,φ(ω,0)+1) = ζφ(ω,0)+1 |
| 2Ɛ2ƐωƐ0+1 = ζζωƐ0+1 |
φ(2,φ(2,φ(ω,0)+1)) = ζζφ(ω,0)+1 |
| 3ƐωƐ0+1 = ηωƐ0+1 |
φ(3,φ(ω,0)+1) = ηφ(ω,0)+1 |
| ωƐ1 = sup(nƐωƐ0+1|n<ω) |
φ(ω,1) = φ(φ(1),1) = sup(φ(n,φ(ω,0)+1)|n<ω) |
| ωƐ2 = sup(nƐωƐ1+1|n<ω) |
φ(ω,2) = φ(φ(1),2) = sup(φ(n,φ(ω,1)+1)|n<ω) |
| ωƐω |
φ(ω,ω) = φ(φ(1),φ(1)) |
| ωƐω+1 |
φ(ω,ω+1) = φ(φ(1),φ(1)+1) |
| ωƐωω |
φ(ω,ωω) = φ(φ(1),φ(φ(1))) |
| ωƐε0 = ωƐ1Ɛ0 |
φ(ω,ε0) = φ(φ(1),φ(1,0)) |
| ωƐζ0 = ωƐ2Ɛ0 |
φ(ω,ζ0) = φ(φ(1),φ(2,0)) |
| ωƐη0 = ωƐ3Ɛ0 |
φ(ω,η0) = φ(φ(1),φ(3,0)) |
| ωƐωƐ0 |
φ(ω,φ(ω,0)) = φ(φ(1),φ(φ(1),0)) |
| ωƐωƐ0+1 |
φ(ω,φ(ω,0)+1) |
| ωƐωƐ0+ω |
φ(ω,φ(ω,0)+ω) = φ(ω,φ(ω,0)+φ(1)) |
| ωƐωƐ0+ε0 |
φ(ω,φ(ω,0)+ε0) = φ(ω,φ(ω,0)+φ(1,0)) |
| ωƐωƐ0×2 |
φ(ω,φ(ω,0)×2) = φ(ω,φ(ω,0)+φ(ω,0)) |
| ωƐωƐ0×ω |
φ(ω,ωφ(ω,0)+1) = φ(ω,φ(φ(ω,0)+1)) |
| ωƐωƐ02 |
φ(ω,ωφ(ω,0)×2) = φ(ω,φ(φ(ω,0)+φ(ω,0))) |
| ωƐωƐ0ω |
φ(ω,ωωφ(ω,0)+1) = φ(ω,φ(φ(φ(ω,0)+1))) |
| ωƐ1ƐωƐ0+1 = ωƐεωƐ0+1 |
φ(ω,εφ(ω,0)+1) = φ(ω,φ(1,φ(ω,0)+1)) |
| ωƐ2ƐωƐ0+1 = ωƐζωƐ0+1 |
φ(ω,ζφ(ω,0)+1) = φ(ω,φ(2,φ(ω,0)+1)) |
| ωƐ3ƐωƐ0+1 = ωƐηωƐ0+1 |
φ(ω,ηφ(ω,0)+1) = φ(ω,φ(3,φ(ω,0)+1)) |
| ωƐωƐ1 = sup(ωƐnƐωƐ0+1|n<ω) |
φ(ω,φ(ω,1)) = sup(φ(ω,φ(n,φ(ω,0)+1))|n<ω) |
| ωƐωƐω |
φ(ω,φ(ω,ω)) = φ(φ(1),φ(φ(1),φ(1))) |
| ωƐωƐωƐ0 |
φ(ω,φ(ω,φ(ω,0))) = φ(φ(1),φ(φ(1),φ(φ(1),0))) |
| ωƐωƐωƐ1 |
φ(ω,φ(ω,φ(ω,1))) = φ(φ(1),φ(φ(1),φ(φ(1),1))) |
| ωƐωƐωƐω |
φ(ω,φ(ω,φ(ω,ω))) = φ(φ(1),φ(φ(1),φ(φ(1),φ(1)))) |
| ωƐωƐωƐωƐ0 |
φ(ω,φ(ω,φ(ω,φ(ω,0)))) = φ(φ(1),φ(φ(1),φ(φ(1),φ(φ(1),0)))) |
| ω+1Ɛ0 = ωƐωƐωƐωƐ... |
φ(ω+1,0) = φ(ω,φ(ω,φ(ω,...))) = φ(φ(1),φ(φ(1),φ(φ(1),...))) |
| 1Ɛω+1Ɛ0+1 = εωƐ0+1 |
φ(1,φ(ω+1,0)+1) = εφ(ω+1,0)+1 |
| 2Ɛω+1Ɛ0+1 = ζωƐ0+1 |
φ(2,φ(ω+1,0)+1) = ζφ(ω+1,0)+1 |
| ωƐω+1Ɛ0+1 = sup(nƐω+1Ɛ0+1|n<ω) |
φ(ω,φ(ω+1,0)+1) = sup(φ(n,φ(ω+1,0)+1)|n<ω) |
| ω+1Ɛ1 = ωƐωƐω...ω+1Ɛ0+1 |
φ(ω+1,1) = φ(ω,φ(ω,φ(ω,φ(ω,... φ(ω+1,0)+1 ...)))) |
| ω+1Ɛω |
φ(ω+1,ω) |
| ω+1ƐωƐ0 |
φ(ω+1,φ(ω,0)) |
| ω+1Ɛω+1Ɛ0 |
φ(ω+1,φ(ω+1,0)) |
| ω+1Ɛω+1Ɛ1 |
φ(ω+1,φ(ω+1,1)) |
| ω+1Ɛω+1Ɛω |
φ(ω+1,φ(ω+1,ω)) |
| ω+1Ɛω+1ƐωƐ0 |
φ(ω+1,φ(ω+1,φ(ω,0))) |
| ω+1Ɛω+1Ɛω+1Ɛ0 |
φ(ω+1,φ(ω+1,φ(ω+1,0))) |
| ω+2Ɛ0 = ω+1Ɛω+1Ɛω+1Ɛω+1Ɛ... |
φ(ω+2,0) = φ(ω+1,φ(ω+1,φ(ω+1,...))) |
| ω+3Ɛ0 = ω+2Ɛω+2Ɛω+2Ɛω+2Ɛ... |
φ(ω+3,0) = φ(ω+2,φ(ω+2,φ(ω+2,...))) |
| ω×2Ɛ0 |
φ(ω×2,0) |
| ω×2Ɛ1 = sup(ω+nƐω×2Ɛ0+1|n<ω) |
φ(ω×2,1) = sup(φ(ω+n,φ(ω×2,0)+1)|n<ω) |
| ω×2Ɛ2 = sup(ω+nƐω×2Ɛ1+1|n<ω) |
φ(ω×2,2) = sup(φ(ω+n,φ(ω×2,1)+1)|n<ω) |
| ω×2Ɛω |
φ(ω×2,ω) |
| ω×2+1Ɛ0 |
φ(ω×2+1,0) = φ(ω×2,φ(ω×2,φ(ω×2,...))) |
| ω×3Ɛ0 |
φ(ω×3,0) |
| ω×4Ɛ0 |
φ(ω×4,0) |
| ω2Ɛ0 |
φ(ω2,0) = φ(φ(2),0) |
| ω3Ɛ0 |
φ(ω3,0) = φ(φ(3),0) |
| ωωƐ0 |
φ(ωω,0) = φ(φ(φ(1)),0) |
| ωωωƐ0 |
φ(ωωω,0) = φ(φ(φ(φ(1))),0) |
| ωωωωƐ0 |
φ(ωωωω,0) = φ(φ(φ(φ(φ(1)))),0) |
| ωωωωωƐ0 |
φ(ωωωωω,0) = φ(φ(φ(φ(φ(φ(1))))),0) |
| 1Ɛ0Ɛ0 |
φ(ε0,0) = φ(φ(1,0),0) = φ(φ(φ(0),0),0) |
| 1Ɛ1Ɛ0 |
φ(ε1,0) = φ(φ(1,1),0) |
| 2Ɛ0Ɛ0 |
φ(ζ0,0) = φ(φ(2,0),0) |
| 3Ɛ0Ɛ0 |
φ(η0,0) = φ(φ(3,0),0) |
| 4Ɛ0Ɛ0 |
φ(φ(4,0),0) |
| ωƐ0Ɛ0 |
φ(φ(ω,0),0) = φ(φ(φ(1),0),0) |
| ω+1Ɛ0Ɛ0 |
φ(φ(ω+1,0),0) |
| ω×2Ɛ0Ɛ0 |
φ(φ(ω×2,0),0) |
| ω2Ɛ0Ɛ0 |
φ(φ(ω2,0),0) |
| ωωƐ0Ɛ0 |
φ(φ(ωω,0),0) |
| 1Ɛ0Ɛ0Ɛ0 |
φ(φ(ε0,0),0) = φ(φ(φ(1,0),0),0) = φ(φ(φ(φ(0),0),0),0) |
| 2Ɛ0Ɛ0Ɛ0 |
φ(φ(ζ0,0),0) = φ(φ(φ(2,0),0),0) |
| 3Ɛ0Ɛ0Ɛ0 |
φ(φ(η0,0),0) = φ(φ(φ(3,0),0),0) |
| ωƐ0Ɛ0Ɛ0 |
φ(φ(φ(ω,0),0),0) = φ(φ(φ(φ(1),0),0),0) |
| 1Ɛ0Ɛ0Ɛ0Ɛ0 |
φ(φ(φ(ε0,0),0),0) = φ(φ(φ(φ(φ(0),0),0),0),0) |
| ωƐ0Ɛ0Ɛ0Ɛ0 |
φ(φ(φ(φ(ω,0),0),0),0) = φ(φ(φ(φ(φ(1),0),0),0),0) |
| 1Ɛ0Ɛ0Ɛ0Ɛ0Ɛ0 |
φ(φ(φ(φ(ε0,0),0),0),0) = φ(φ(φ(φ(φ(φ(0),0),0),0),0),0) |
| Г0 = ...Ɛ0Ɛ0Ɛ0Ɛ0Ɛ0 |
φ(1,0,0) = φ(φ(φ(φ(φ(φ(...,0),0),0),0),0),0) |
| Г0+1 |
φ(1,0,0)+1 = φ(1,0,0)+φ(0) |
| Г0+ω |
φ(1,0,0)+φ(1) |
| Г0+ε0 |
φ(1,0,0)+φ(1,0) |
| Г0×2 |
φ(1,0,0)+φ(1,0,0) |
| ωГ0+1 = 0ƐГ0+1 = Г0×ω |
φ(Г0+1) = φ(φ(1,0,0)+1) |
| ωГ0×2 = 0ƐГ0×2 = Г02 |
φ(Г0+Г0) = φ(φ(1,0,0)+φ(1,0,0)) |
| ωωГ0+1 = 0Ɛ0ƐГ0+1 = Г0ω |
φ(φ(Г0+1)) = φ(φ(φ(1,0,0)+1)) |
| ωωГ0×2 = 0Ɛ0ƐГ0×2 = Г0Г0 |
φ(φ(Г0×2)) = φ(φ(φ(1,0,0)+φ(1,0,0))) |
| ωωωГ0+1 = 0Ɛ0Ɛ0ƐГ0+1 = Г0Г0ω |
φ(φ(φ(Г0+1))) = φ(φ(φ(φ(1,0,0)+1))) |
| ωωωГ0×2 = 0Ɛ0Ɛ0ƐГ0×2 = Г0Г0Г0 |
φ(φ(φ(Г0×2))) = φ(φ(φ(φ(1,0,0)+φ(1,0,0)))) |
| ωωωωГ0+1 = 0Ɛ0Ɛ0Ɛ0ƐГ0+1 = Г0Г0Г0ω |
φ(φ(φ(φ(Г0+1)))) = φ(φ(φ(φ(φ(1,0,0)+1)))) |
| εГ0+1 = 1ƐГ0+1 = ωωω...Г0+1 = Г0Г0Г0Г0... |
φ(1,Г0+1) = φ(φ(φ(φ(...φ(1,0,0)+1...)))) |
| ζГ0+1 = 2ƐГ0+1 = εεε...Г0+1 |
φ(2,Г0+1) = φ(1,φ(1,φ(1,φ(1,...φ(1,0,0)+1...)))) |
| ηГ0+1 = 3ƐГ0+1 = ζζζ...Г0+1 |
φ(3,Г0+1) = φ(2,φ(2,φ(2,φ(2,...φ(1,0,0)+1...)))) |
| ωƐГ0+1 |
φ(ω,Г0+1) = φ(φ(1),φ(1,0,0)+1) |
| ωƐ0ƐГ0+1 |
φ(φ(ω,0),Г0+1) = φ(φ(φ(1),0),φ(1,0,0)+1) |
| ωωƐ0ƐГ0+1 |
φ(φ(ωω,0),Г0+1) = φ(φ(φ(φ(1)),0),φ(1,0,0)+1) |
| 1Ɛ0Ɛ0ƐГ0+1 |
φ(φ(ε0,0),Г0+1) = φ(φ(φ(1,0),0),φ(1,0,0)+1) |
| 2Ɛ0Ɛ0ƐГ0+1 |
φ(φ(ζ0,0),Г0+1) = φ(φ(φ(2,0),0),φ(1,0,0)+1) |
| ωƐ0Ɛ0ƐГ0+1 |
φ(φ(φ(ω,0),0),Г0+1) = φ(φ(φ(φ(1),0),0),φ(1,0,0)+1) |
| ωƐ0Ɛ0Ɛ0ƐГ0+1 |
φ(φ(φ(φ(ω,0),0),0),Г0+1) = φ(φ(φ(φ(φ(1,0),0),0),0),φ(1,0,0)+1) |
| Г0Ɛ1 = ...Ɛ0Ɛ0Ɛ0Ɛ0ƐГ0+1 |
φ(Г0,1) = φ(φ(1,0,0),1) = φ(φ(φ(φ(...,0),0),0),φ(1,0,0)+1) |
| ωГ0Ɛ1+1 = 0ƐГ0Ɛ1+1 |
φ(φ(Г0,1)+1) = φ(φ(φ(1,0,0),1)+1) |
| εГ0Ɛ1+1 = 1ƐГ0Ɛ1+1 = ωωω...Г0Ɛ1+1 |
φ(1,φ(Г0,1)+1) = φ(φ(φ(φ(...φ(φ(1,0,0),1)+1...)))) |
| ζГ0Ɛ1+1 = 2ƐГ0Ɛ1+1 = εεε...Г0Ɛ1+1 |
φ(2,φ(Г0,1)+1) = φ(1,φ(1,φ(1,φ(1,...φ(φ(1,0,0),1)+1...)))) |
| ηГ0Ɛ1+1 = 3ƐГ0Ɛ1+1 = ζζζ...Г0Ɛ1+1 |
φ(3,φ(Г0,1)+1) = φ(2,φ(2,φ(2,φ(2,...φ(φ(1,0,0),1)+1...)))) |
| ωƐГ0Ɛ1+1 |
φ(ω,φ(Г0,1)+1) = φ(φ(1,0),φ(φ(1,0,0),1)+1) |
| ωƐ0ƐГ0Ɛ1+1 |
φ(φ(ω,0),φ(Г0,1)+1) = φ(φ(φ(1,0),0),φ(φ(1,0,0),1)+1) |
| ωƐ0Ɛ0ƐГ0Ɛ1+1 |
φ(φ(φ(ω,0),0),φ(Г0,1)+1) = φ(φ(φ(φ(1,0),0),0),φ(φ(1,0,0),1)+1) |
| ωƐ0Ɛ0Ɛ0ƐГ0Ɛ1+1 |
φ(φ(φ(φ(ω,0),0),0),φ(Г0,1)+1) = φ(φ(φ(φ(φ(1,0),0),0),0),φ(φ(1,0,0),1)+1) |
| Г0Ɛ2 = ...Ɛ0Ɛ0Ɛ0Ɛ0ƐГ0Ɛ1+1 |
φ(Г0,2) = φ(φ(1,0,0),2) = φ(φ(φ(φ(...,0),0),0),φ(φ(1,0,0),1)+1) |
| Г0Ɛ3 = ...Ɛ0Ɛ0Ɛ0Ɛ0ƐГ0Ɛ2+1 |
φ(Г0,3) = φ(φ(1,0,0),3) = φ(φ(φ(φ(...,0),0),0),φ(φ(1,0,0),2)+1) |
| Г0Ɛω = Г0Ɛ0Ɛ0 |
φ(Г0,ω) = φ(φ(1,0,0),φ(0)) |
| Г0Ɛε0 = Г0Ɛ1Ɛ0 |
φ(Г0,ε0) = φ(φ(1,0,0),φ(1,0)) |
| Г0Ɛζ0 = Г0Ɛ2Ɛ0 |
φ(Г0,ζ0) = φ(φ(1,0,0),φ(2,0)) |
| Г0Ɛη0 = Г0Ɛ3Ɛ0 |
φ(Г0,η0) = φ(φ(1,0,0),φ(3,0)) |
| Г0ƐωƐ0 |
φ(Г0,φ(ω,0)) = φ(φ(1,0,0),φ(φ(0),0)) |
| Г0ƐωƐ0Ɛ0 |
φ(Г0,φ(φ(ω,0),0)) = φ(φ(1,0,0),φ(φ(φ(0),0),0)) |
| Г0ƐωƐ0Ɛ0Ɛ0 |
φ(Г0,φ(φ(φ(ω,0),0),0)) = φ(φ(1,0,0),φ(φ(φ(φ(0),0),0),0)) |
| Г0ƐωƐ0Ɛ0Ɛ0Ɛ0 |
φ(Г0,φ(φ(φ(φ(ω,0),0),0),0)) = φ(φ(1,0,0),φ(φ(φ(φ(φ(0),0),0),0),0)) |
| Г0ƐГ0 = Г0Ɛ...Ɛ0Ɛ0Ɛ0Ɛ0 |
φ(Г0,Г0) = φ(φ(1,0,0),φ(1,0,0)) = φ(φ(1,0,0),φ(φ(φ(φ(φ(...,0),0),0),0),0)) |
| Г0ƐГ0+1 |
φ(Г0,Г0+1) = φ(φ(1,0,0),φ(1,0,0)+1) |
| Г0ƐГ0×2 |
φ(Г0,Г0+Г0) = φ(φ(1,0,0),φ(1,0,0)+φ(1,0,0)) |
| Г0ƐωГ0+1 = Г0Ɛ0ƐГ0+1 |
φ(Г0,φ(Г0+1)) = φ(φ(1,0,0),φ(φ(1,0,0)+1)) |
| Г0ƐωГ0×2 = Г0Ɛ0ƐГ0×2 |
φ(Г0,φ(Г0+Г0)) = φ(φ(1,0,0),φ(φ(1,0,0)+φ(1,0,0))) |
| Г0ƐωωГ0+1 = Г0Ɛ0Ɛ0ƐГ0+1 |
φ(Г0,φ(φ(Г0+1))) = φ(φ(1,0,0),φ(φ(φ(1,0,0)+1))) |
| Г0ƐεГ0+1 = Г0Ɛ1ƐГ0+1 |
φ(Г0,φ(1,Г0+1)) = φ(φ(1,0,0),φ(1,φ(1,0,0)+1)) |
| Г0ƐГ0Ɛ1 = Г0Ɛ...Ɛ0Ɛ0Ɛ0ƐГ0+1 |
φ(Г0,φ(Г0,1)) = φ(φ(1,0,0),φ(φ(1,0,0),1) = φ(φ(1,0,0),φ(φ(φ(...,0),0),φ(1,0,0)+1)) |
| Г0ƐГ0ƐГ0 |
φ(Г0,φ(Г0,Г0)) = φ(φ(1,0,0),φ(φ(1,0,0),φ(1,0,0))) |
| Г0ƐГ0ƐГ0ƐГ0 |
φ(Г0,φ(Г0,φ(Г0,Г0))) = φ(φ(1,0,0),φ(φ(1,0,0),φ(φ(1,0,0),φ(1,0,0)))) |
| Г0+1Ɛ0 = Г0ƐГ0ƐГ0Ɛ... |
φ(Г0+1,0) = φ(φ(1,0,0)+1,0) = φ(Г0,φ(Г0,φ(Г0,φ(Г0,...)))) |
| ωГ0+1Ɛ0+1 = 0ƐГ0+1Ɛ0+1 |
φ(φ(Г0+1,0)+1) = φ(φ(φ(1,0,0)+1,0)+1) = ωφ(Г0+1,0) |
| εГ0+1Ɛ0+1 = 1ƐГ0+1Ɛ0+1 = ωωω...Г0+1Ɛ0+1 |
φ(1,φ(Г0+1,0)+1) = φ(φ(φ(φ(...φ(φ(1,0,0)+1,0)+1...)))) = εφ(Г0+1,0)+1 |
| Г0ƐГ0+1Ɛ0+1 . |
φ(Г0,φ(Г0+1,0)+1) = φ(φ(1,0,0),φ(φ(1,0,0)+1,0)+1) |
| Г0+1Ɛ1 = Г0ƐГ0Ɛ...Г0+1Ɛ0+1 |
φ(Г0+1,1) = φ(φ(1,0,0)+1,1) = φ(Г0,φ(Г0,φ(Г0,φ(Г0,...φ(Г0+1,0)+1...)))) |
| Г0+1ƐГ0 = Г0+1Ɛ...Ɛ0Ɛ0Ɛ0Ɛ0 |
φ(Г0+1,Г0) = φ(φ(1,0,0)+1,φ(1,0,0)) = φ(φ(1,0,0)+1,φ(φ(φ(...,0),0),0)) |
| Г0+2Ɛ0 = Г0+1ƐГ0+1ƐГ0+1Ɛ... |
φ(Г0+2,0) = φ(φ(1,0,0)+1,0) = φ(Г0+1,φ(Г0+1,φ(Г0+1,φ(Г0+1,...)))) |
| Г0+ωƐ0 |
φ(Г0+ω,0) = φ(φ(1,0,0)+φ(1),0) |
| Г0+ε0Ɛ0 = Г0+1Ɛ0Ɛ0 |
φ(Г0+ε0,0) = φ(φ(1,0,0)+φ(1,0),0) |
| Г0+ωƐ0Ɛ0 |
φ(Г0+φ(ω,0),0) = φ(φ(1,0,0)+φ(φ(1),0),0) |
| Г0+Г0Ɛ0 = (Г0+...Ɛ0Ɛ0Ɛ0Ɛ0)Ɛ0 |
φ(Г0×2,0) = φ(φ(1,0,0)+φ(1,0,0),0) |
| ωГ0+1Ɛ0 = 0ƐГ0+1Ɛ0 |
φ(φ(Г0+1),0) = φ(φ(φ(1,0,0)+1),0) = φ(ωГ0+1,0) |
| ωωГ0+1Ɛ0 = 0Ɛ0ƐГ0+1Ɛ0 |
φ(φ(φ(Г0+1)),0) = φ(φ(φ(φ(1,0,0)+1)),0) = φ(ωωГ0+1,0) |
| εГ0+1Ɛ0 = 1ƐГ0+1Ɛ0 |
φ(φ(1,Г0+1),0) = φ(φ(1,φ(1,0,0)+1),0) = φ(εГ0+1,0) |
| ζГ0+1Ɛ0 = 2ƐГ0+1Ɛ0 |
φ(φ(2,Г0+1),0) = φ(φ(2,φ(1,0,0)+1),0) = φ(ζГ0+1,0) |
| ηГ0+1Ɛ0 = 3ƐГ0+1Ɛ0 |
φ(φ(3,Г0+1),0) = φ(φ(3,φ(1,0,0)+1),0) = φ(ηГ0+1,0) |
| ωƐГ0+1Ɛ0 |
φ(φ(ω,Г0+1),0) = φ(φ(φ(1),φ(1,0,0)+1),0) |
| ωƐ0ƐГ0+1Ɛ0 |
φ(φ(φ(ω,0),Г0+1),0) = φ(φ(φ(φ(1),0),φ(1,0,0)+1),0) |
| Г0Ɛ1Ɛ0 = ...Ɛ0Ɛ0Ɛ0ƐГ0+1Ɛ0 |
φ(φ(Г0,1),0) = φ(φ(φ(1,0,0),1),0) = φ(φ(φ(φ(φ(...,0),0),0),φ(1,0,0)+1),0) |
| Г0Ɛ1Ɛ1 = ...Ɛ0Ɛ0Ɛ0Ɛ0ƐГ0Ɛ1Ɛ0+1 |
φ(φ(Г0,1),1) = φ(φ(φ(1,0,0),1),1) = φ(φ(φ(φ(...,0),0),0),φ(φ(φ(1,0,0),1),0)) |
| Г0Ɛ1Ɛω |
φ(φ(Г0,1),ω) = φ(φ(φ(1,0,0),1),φ(1)) |
| Г0Ɛ1+1Ɛ0 = Г0Ɛ1ƐГ0Ɛ1Ɛ... |
φ(φ(Г0,1)+1,0) = φ(φ(φ(1,0,0),1)+1,0) = φ(φ(Г0,1),φ(φ(Г0,1),φ(φ(Г0,1),...))) |
| Г0Ɛ1+Г0Ɛ1Ɛ0 |
φ(φ(Г0,1)×2,0) = φ(φ(φ(1,0,0),1)+φ(φ(1,0,0),1),0) |
| 0ƐГ0Ɛ1+1Ɛ0 |
φ(φ(φ(Г0,1)+1),0) = φ(ωφ(Г0,1)+1,0) |
| 1ƐГ0Ɛ1+1Ɛ0 |
φ(φ(1,φ(Г0,1)+1),0) = φ(εφ(Г0,1)+1,0) |
| ωƐГ0Ɛ1+1Ɛ0 |
φ(φ(ω,φ(Г0,1)+1),0) = φ(φ(φ(1),φ(φ(1,0,0),1)+1),0) |
| Г0Ɛ2Ɛ0 = ...Ɛ0Ɛ0Ɛ0ƐГ0Ɛ1+1Ɛ0 |
φ(φ(Г0,2),0) = φ(φ(φ(1,0,0),2),0) = φ(φ(φ(φ(...,0),0),φ(φ(1,0,0),1)+1),0) |
| Г0ƐωƐ0 |
φ(φ(Г0,ω),0) = φ(φ(φ(1,0,0),φ(1)),0) |
| Г0+1Ɛ0Ɛ0 = Г0ƐГ0ƐГ0Ɛ...Ɛ0 |
φ(φ(Г0+1,0),0) = φ(φ(φ(1,0,0)+1,0),0) = φ(φ(Г0,φ(Г0,φ(Г0,φ(Г0,...)))),0) |
| 0ƐГ0+1Ɛ0Ɛ0 |
φ(φ(φ(Г0+1,0)),0) = φ(φ(ωГ0+1,0),0) |
| 1ƐГ0+1Ɛ0Ɛ0 |
φ(φ(φ(1,Г0+1),0),0) = φ(φ(εГ0+1,0),0) |
| ωƐГ0+1Ɛ0Ɛ0 |
φ(φ(φ(ω,Г0+1),0),0) = φ(φ(φ(φ(1),φ(1,0,0)+1),0),0) |
| ωƐ0ƐГ0+1Ɛ0Ɛ0 |
φ(φ(φ(φ(ω,0),Г0+1),0),0) = φ(φ(φ(φ(φ(1),0),φ(1,0,0)+1),0),0) |
| Г0Ɛ1Ɛ0Ɛ0 = ...Ɛ0Ɛ0ƐГ0+1Ɛ0Ɛ0 |
φ(φ(φ(Г0,1),0),0) = φ(φ(φ(φ(1,0,0),1),0),0) = φ(φ(φ(φ(φ(...,0),0),φ(1,0,0)+1),0),0) |
| Г0+1Ɛ0Ɛ0Ɛ0 = Г0ƐГ0ƐГ...Ɛ0Ɛ0 |
φ(φ(φ(Г0+1,0),0),0) = φ(φ(φ(φ(1,0,0)+1,0),0),0) = φ(φ(φ(Г0,φ(Г0,φ(Г0,φ(Г0,...)))),0),0) |
| Г1 = Г0+1...Ɛ0Ɛ0Ɛ0 |
φ(1,0,1) = φ(φ(φ(φ(...φ(1,0,0)+1...,0),0),0),0) |
| εГ1+1 = 1ƐГ1+1 = ωωω...Г1+1 |
φ(1,Г1+1) = φ(φ(φ(φ(...φ(1,0,1)+1...)))) |
| ωƐГ1+1 |
φ(ω,Г1+1) = φ(φ(1),φ(1,0,1)+1) |
| Г0ƐГ1+1 = ...Ɛ0Ɛ0Ɛ0Ɛ0ƐГ1+1 |
φ(Г0,Г1+1) = φ(φ(1,0,0),φ(1,0,1)+1) |
| Г1Ɛ1 = Г0+1...Ɛ0Ɛ0ƐГ1+1 |
φ(Г1,1) = φ(φ(φ(φ(φ(...φ(1,0,0)+1...,0),0),0),0),φ(1,0,1)+1) |
| Г1Ɛ2 = Г0+1...Ɛ0Ɛ0ƐГ1Ɛ1+1 |
φ(Г1,2) = φ(φ(φ(φ(φ(...φ(1,0,0)+1...,0),0),0),0),φ(φ(1,0,1),1)+1) |
| Г1ƐГ0 = Г1Ɛ...Ɛ0Ɛ0Ɛ0Ɛ0 |
φ(Г1,Г0) = φ(φ(1,0,1),φ(1,0,0)) = φ(φ(1,0,1),φ(φ(φ(φ(...,0),0),0),0)) |
| Г1ƐГ1 = Г1ƐГ0+1...Ɛ0Ɛ0 |
φ(Г1,Г1) = φ(φ(1,0,1),φ(1,0,1)) = φ(φ(1,0,1),φ(φ(φ(φ(...φ(1,0,0)+1...,0),0),0),0)) |
| Г1+1Ɛ0 = Г1ƐГ1ƐГ1Ɛ... |
φ(Г1+1,0) = φ(φ(1,0,1)+1,0) = φ(Г1,φ(Г1,φ(Г1,φ(Г1,...)))) |
| Г1+Г0Ɛ0 = (Г1+...Ɛ0Ɛ0Ɛ0Ɛ0)Ɛ0 |
φ(Г1+Г0,0) = φ(φ(1,0,1)+φ(1,0,0),0) |
| Г1+Г1Ɛ0 = (Г1+Г0+1...Ɛ0Ɛ0)Ɛ0 |
φ(Г1×2,0) = φ(φ(1,0,1)+φ(1,0,1),0) |
| ωГ1+1Ɛ0 = 0ƐГ1+1Ɛ0 |
φ(φ(Г1+1),0) = φ(φ(φ(1,0,1)+1),0) = φ(ωГ1+1,0) |
| ωωГ1+1Ɛ0 = 0Ɛ0ƐГ1+1Ɛ0 |
φ(φ(φ(Г1+1)),0) = φ(φ(φ(φ(1,0,1)+1)),0) = φ(ωωГ1+1,0) |
| εГ1+1Ɛ0 = 1ƐГ1+1Ɛ0 |
φ(φ(1,Г1+1),0) = φ(φ(1,φ(1,0,1)+1),0) = φ(εГ1+1,0) |
| Г0ƐГ1+1Ɛ0 = ...Ɛ0Ɛ0Ɛ0ƐГ1+1Ɛ0 |
φ(φ(Г0,Г1+1),0) = φ(φ(φ(1,0,0),φ(1,0,1)+1),0) |
| Г1Ɛ1Ɛ0 = Г0+1...Ɛ0ƐГ1+1Ɛ0 |
φ(φ(Г1,1),0) = φ(φ(φ(φ(φ(...φ(1,0,0)+1...,0),0),0),φ(1,0,1)+1),0) |
| Г1Ɛ1Ɛ0Ɛ0 = Г0+1...Ɛ0ƐГ1+1Ɛ0Ɛ0 |
φ(φ(φ(Г1,1),0),0) = φ(φ(φ(φ(φ(φ(...φ(1,0,0)+1...,0),0),0),φ(1,0,1)+1),0) ,0) |
| Г2 = Г1+1...Ɛ0Ɛ0Ɛ0 |
φ(1,0,2) = φ(φ(φ(φ(...φ(1,0,1)+1...,0),0),0),0) |
| Гω |
φ(1,0,φ(1)) |
| Гε0 = Г1Ɛ0 |
φ(1,0,φ(1,0)) |
| ГωƐ0 |
φ(1,0,φ(φ(1),0)) |
| Гε0Ɛ0 = Г1Ɛ0Ɛ0 |
φ(1,0,φ(φ(1,0),0)) |
| ГωƐ0Ɛ0 |
φ(1,0,φ(φ(φ(1),0),0)) |
| ГГ0 = Г...Ɛ0Ɛ0Ɛ0Ɛ0 |
φ(1,0,φ(1,0,0)) = φ(1,0,φ(φ(φ(φ(...,0),0),0),0)) |
| ГГ1 = Г Г0+1...Ɛ0Ɛ0Ɛ0 |
φ(1,0,φ(1,0,1)) = φ(1,0,φ(φ(φ(...φ(1,0,0)+1...,0),0),0)) |
| ГГГ0 |
φ(1,0,φ(1,0,φ(1,0,0))) |
| ГГГГ0 |
φ(1,0,φ(1,0,φ(1,0,φ(1,0,0)))) |
| 1Г0 = ГГГГ... |
φ(1,1,0) = φ(1,0,φ(1,0,φ(1,0,φ(1,0,...)))) |
| 0Ɛ1Г0+1 = ω1Г0+1 = 1Г0×ω |
φ(φ(1,1,0)+1) |
| 1Ɛ1Г0+1 = ε1Г0+1 |
φ(1,φ(1,1,0)+1) |
| Г0Ɛ1Г0+1 = ...Ɛ0Ɛ0Ɛ0Ɛ0Ɛ1Г0+1 |
φ(φ(1,0,0),φ(1,1,0)+1) = φ(φ(1,φ(1,φ(1,...))),φ(1,1,0)+1) |
| Г1Ɛ1Г0+1 = Г0+1...Ɛ0Ɛ0Ɛ1Г0+1 |
φ(φ(1,0,1),φ(1,1,0)+1) = φ(φ(φ(φ(...φ(1,0,0)+1...,0),0),0),φ(1,1,0)+1) |
| 1Г0Ɛ1 = ГГГ... Ɛ1Г0+1 |
φ(φ(1,1,0),1) = φ(φ(1,0,φ(1,0,φ(1,0,...))),φ(1,1,0)+1) |
| 1Г0+1Ɛ0 = 1Г0Ɛ1Г0Ɛ1Г0ƐГ... |
φ(φ(1,1,0)+1,0) = φ(φ(1,1,0),φ(φ(1,1,0),φ(φ(1,1,0),...))) |
| Г1Г0+1 = 0Г1Г0+1 = 1Г0+1...Ɛ0Ɛ0Ɛ0 |
φ(1,0,φ(1,1,0)+1) = φ(φ(φ(φ(...φ(1,1,0)+1...,0),0),0),0) |
| Г1Г0+2 = 0Г1Г0+2 = Г1Г0+1+1...Ɛ0Ɛ0Ɛ0 |
φ(1,0,φ(1,1,0)+2) = φ(φ(φ(φ(...φ(1,0,φ(1,1,0)+1)+1...,0),0),0),0) |
| Г1Г0×2 = 0Г1Г0×2 |
φ(1,0,φ(1,1,0)+φ(1,1,0)) |
| Гω1Г0+1 = 0Г1Г0×ω = Г0Ɛ1Г0+1 |
φ(1,0,φ(φ(1,1,0)+1)) |
| ГεГ1+1 = 0Г1Ɛ1Г0+1 |
φ(1,0,φ(1,φ(1,1,0)+1)) |
| ГГ1Г0+1 = 0Г0Г1Г0+1 |
φ(1,0,φ(1,0,φ(1,1,0)+1)) |
| 1Г1 = ГГГ...1Г0+1 |
φ(1,1,1) = φ(1,0,φ(1,0,φ(1,0,φ(1,0,...φ(1,1,0)+1...)))) |
| 2Г0 = 1Г1Г1Г1Г... |
φ(1,2,0) = φ(1,1,φ(1,1,φ(1,1,φ(1,1,...)))) |
| ωГ0 |
φ(1,ω,0) = φ(1,φ(1),0) |
| ωωГ0 |
φ(1,ωω,0) = φ(1,φ(φ(1)),0) |
| 1Ɛ0Г0 = ε0Г0 |
φ(1,ε0,0) = φ(1,φ(1,0),0) |
| Г0Г0 = ...Ɛ0Ɛ0Ɛ0Ɛ0Г0 |
φ(1,Г0,0) = φ(1,φ(1,0,0),0) = φ(1,φ(φ(φ(φ(...,0),0),0),0),0) |
| Г1Г0 = Г0+1...Ɛ0Ɛ0Ɛ0Г0 |
φ(1,Г1,0) = φ(1,φ(1,0,1),0) = φ(1,φ(φ(φ(φ(...φ(1,0,0)+1...,0),0),0),0),0) |
| 1Г0Г0 = ГГГ...Г0 |
φ(1,φ(1,1,0),0) = φ(1,φ(1,0,φ(1,0,φ(1,0,...))),0) |
| ωГ0Г0 |
φ(1,φ(1,φ(1),0),0) |
| ε0Г0Г0 |
φ(1,φ(1,φ(1,0),0),0) |
| Г0Г0Г0 |
φ(1,φ(1,φ(1,0,0),0),0) |
| Г0Г0Г0Г0 |
φ(1,φ(1,φ(1,φ(1,0,0),0),0),0) |
| P0 = ...Г0Г0Г0Г0 |
φ(2,0,0) = φ(1,φ(1,φ(1,φ(1,φ(1,...,0),0),0),0),0) |
| ωP0+1 = 0ƐP0+1 |
φ(φ(2,0,0)+1) |
| εP0+1 = 1ƐP0+1 = ωωω...P0+1 |
φ(1,φ(2,0,0)+1) = φ(φ(φ(φ(...φ(2,0,0)+1...)))) |
| Г0ƐP0+1 = ...Ɛ0Ɛ0Ɛ0Ɛ0ƐP0+1 |
φ(φ(1,0,0),φ(2,0,0)+1) = φ(φ(φ(φ(φ(...,0),0),0),0),φ(2,0,0)+1) |
| P0Ɛ1 = ...Г0Г0Г0ƐP0+1 |
φ(φ(2,0,0),1) = φ(φ(1,φ(1,φ(1,φ(1,...,0),0),0),0),φ(2,0,0)+1) |
| P0+1Ɛ0 = P0ƐP0ƐP0Ɛ... |
φ(φ(2,0,0)+1,0) = φ(φ(2,0,0),φ(φ(2,0,0),φ(φ(2,0,0),...))) |
| ГP0+1 = P0+1...Ɛ0Ɛ0Ɛ0 |
φ(1,0,φ(2,0,0)+1) = φ(φ(φ(φ(...φ(2,0,0)+1...0),0),0),0) |
| 1ГP0+1 = ГГГ...P0+1 |
φ(1,1,φ(2,0,0)+1) = φ(1,0,φ(1,0,φ(1,0,φ(1,0,...φ(2,0,0)+1...)))) |
| ωГP0+1 |
φ(1,ω,φ(2,0,0)+1) = φ(1,φ(1),φ(2,0,0)+1) |
| ε0ГP0+1 |
φ(1,ε0,φ(2,0,0)+1) = φ(1,φ(1,0),φ(2,0,0)+1) |
| Г0ГP0+1 = ...Ɛ0Ɛ0Ɛ0Ɛ0ГP0+1 |
φ(1,Г0,φ(2,0,0)+1) = φ(1,φ(1,0,0),φ(2,0,0)+1) |
| P0Г1 = ...Г0Г0Г0Г0ГP0+1 |
φ(1,φ(2,0,0),1) = φ(1,φ(1,φ(1,φ(1,...,0),0),0),φ(2,0,0)+1) |
| P0Г2 = ...Г0Г0Г0Г0ГР0Г1+1 |
φ(1,φ(2,0,0),2) = φ(1,φ(1,φ(1,φ(1,...,0),0),0),φ(1,φ(2,0,0),1)+1) |
| P0+1Г0 = P0ГP0ГP0Г... |
φ(1,φ(2,0,0)+1,0) = φ(1,φ(2,0,0),φ(1,φ(2,0,0),φ(1,φ(2,0,0),...))) |
| ωP0+1Г0 = 0ƐP0+1Г0 |
φ(1,φ(φ(2,0,0)+1),0) |
| εP0+1Г0 = 1ƐP0+1Г0 |
φ(1,φ(1,φ(2,0,0)+1),0) |
| ГP0+1Г0 = 0ГP0+1Г0 |
φ(1,φ(1,0,φ(2,0,0)+1),0) |
| 1ГP0+1Г0 = ГГ...P0+1Г0 |
φ(1,φ(1,1,φ(2,0,0)+1),0) = φ(1,φ(1,0,φ(1,0,...φ(2,0,0)+1...)),0) |
| P0Г1Г0 = ...Г0Г0Г0ГP0+1Г0 |
φ(1,φ(1,φ(2,0,0),1),0) = φ(φ(1,φ(1,φ(1,...,0),0),φ(2,0,0)+1),0) |
| P0+1Г0Г0 = P0ГP0Г...Г0 |
φ(1,φ(1,φ(2,0,0)+1,0),0) = φ(1,φ(1,φ(2,0,0),φ(1,φ(2,0,0),φ(1,φ(2,0,0),...))),0) |
| P1 = P0+1...Г0Г0Г0 |
φ(2,0,1) = φ(1,φ(1,φ(1,φ(1,φ(1,...φ(2,0,0)+1...,0),0),0),0),0) |
| 1P0 = PPPP... |
φ(2,1,0) = φ(2,0,φ(2,0,φ(2,0,φ(2,0,...)))) |
| B0 = ...P0P0P0P |
φ(3,0,0) = φ(2,φ(2,φ(2,φ(2,φ(2,...,0),0),0),0),0) |
| Ординал Аккермана |
φ(1,0,0,0) = φ(φ(φ(φ(φ(φ(...,0,0),0,0),0,0),0,0),0,0),0,0) |
таб.18 (Сравнение ординальных нотаций Веблена и Кантора)
Вот такой длинный получился перечень сопоставлений. Если в ходе изучения этой таблицы вы еще не поняли как Функция Веблена учитывает ординалы, то сейчас я расскажу об этом немного подробнее. Нормальная форма функции позволяет записать любой ординал, какой только может создать функция, с использованием "0", собственно функции φ(...), которая принимает в себя любое количество аргументов, и операции сложения. Если мы используем только один аргумент функции, то это в точности повторяет ординальную нотацию Кантора, так что φ(n) = ωn. Формально единица в нотации Кантора записывалась так 1 = ω0, следовательно в нотации Веблена единица будет записываться так 1 = φ(0). Ну а, скажем тройка, формально в нотации Кантора это 3 = ω0+ω0+ω0, тогда в нотации Веблена, она формально будет записана так 3 = φ(0)+φ(0)+φ(0). По сути своей ординальные нотации не слишком заморачиваются с записью натуральных чисел, в большинстве своем для их формальной записи используется самый простейший способ, известный еще первобытным людям, обычный натуралый вид, как зарубки на дереве. Оно и понятно, ведь данные нотации нацелены на запись ординалов, а это куда бо́льший класс чисел, для учета которого потребуются все возможности ординальных функций и нечего их растрачивать на какой-то особый способ записи обычных натуральных чисел. Но поскольку привычнее воспринимать натуральные числа в десятичной нотации, то так мы их и будем записывать внутри нотации Веблена. В общем, получается что до уровня ε0 функция Веблена повторяет путь нотации Кантора, только используя иной вид записи, вместо степенных башен из ω, мы городим вложенные φ(n).
Но начиная с ε0, функция Веблена задействует больше одного аргумента и тут уже начинается учет неподвижных точек. Давайте выделим из всего этого перечня неподвижных точек очень важные ординалы, которые назовем основными неподвижными точками разных разрядов. Основная неподвижная точка первого разряда это φ(1,0) = ε0 - предел последовательности степенных башен из ω (PTO ACA0). Основной неподвижной точкой второго разряда станет φ(1,0,0) = Г0 - предел ограничено квантифицированных рекурсий над ω (PTO ATR0). Ну а Ординал Аккермана φ(1,0,0,0) тогда получается уже является основной неподвижной точкой третьего разряда, пусть для него и нет теории, пределом которой он бы являлся, но все равно это "круглый ординал", если можно так выразиться. Перед тем как двигаться дальше, давайте еще раз проследим как именно поэтапно создаются эти основные неподвижные точки:
φ(1,0) = первая неподвижная точка α↦φ(α)
φ(1,1) = вторая неподвижная точка α↦φ(α)
φ(2,0) = первая неподвижная точка α↦φ(1,α)
φ(2,1) = вторая неподвижная точка α↦φ(1,α)
φ(1,0,0) = первая неподвижная точка α↦φ(α,0)
φ(1,0,1) = вторая неподвижная точка α↦φ(α,0)
φ(1,1,0) = первая неподвижная точка α↦φ(1,0,α)
φ(1,1,1) = вторая неподвижная точка α↦φ(1,0,α)
φ(2,0,0) = первая неподвижная точка α↦φ(1,α,0)
φ(2,0,1) = вторая неподвижная точка α↦φ(1,α,0)
φ(2,1,0) = первая неподвижная точка α↦φ(2,0,α)
φ(2,1,1) = вторая неподвижная точка α↦φ(2,0,α)
φ(3,0,0) = первая неподвижная точка α↦φ(2,α,0)
φ(3,0,1) = вторая неподвижная точка α↦φ(2,α,0)
φ(1,0,0,0) = первая неподвижная точка α↦φ(α,0,0)
Чем-то подобный учет основных неподвижных точек похож на привычную нам позиционную десятичную нотацию натуральных чисел, в которой так же есть разряды. Разница в том как увеличиваются эти разряды. Когда в десятичной нотации мы складываем числа в столбик, и в предыдущем разряде числа девятка увеличивается на единицу, то она превращается в ноль, но зато мы на единицу увеличиваем цифру из следующего разряда: ...xx9(+1)00... = ...xx(+1)000..., например: 1390 + 10 = 1400. Тогда как в нотации Веблена разряд увеличивается на единицу когда в предыдущем разряде происходит бесконечное подставления функции самой в себя φω(...,x,x,n,0,0,...) = φ(...,x,x(+1),0,0,0,...), например: φ(1,3,0) = φ(1,2,φ(1,2,φ(1,2,φ(1,2,...)))). То есть увеличение разядов φ(...,x,x(+1),0,0,0,...) происходит, когда функция по отношению к предыдущему разряду α↦φ(...,x,x,α,0,0,...) становится неподвижной точкой.
Ну а дальше, зная как образуются эти основные неподвижные точки разных разрядов, мы с легкостью доберемся до пределов Функции Веблена:
φ(1,0,0,0,0) = неподвижная точка α↦φ(α,0,0,0) - основная неподвижная точка четветого разряда
φ(1,0,0,0,0,0) = неподвижная точка α↦φ(α,0,0,0,0) - основная неподвижная точка пятого разряда
φ(1,0,0,0,0,0,0) = неподвижная точка α↦φ(α,0,0,0,0,0) - основная неподвижная точка шестого разряда
φ(1,0,0,0,0,0,0,...,0) = неподвижная точка α↦φ(α,0,0,0,0,0,...,0) - основная неподвижная точка n-ого разряда
Но на самом деле это еще не полный предел ординальной Функции Веблена, ведь мы можем создать основную неподвижную точку ω-разряда или любого другого траснфинитно-ордианльного разряда. Правила записи таких ординалов в рамках Функции Веблена придумал немецкий математик Курт Шутте, он предложил преобразовать массиный вид Функции Веблена в матричный вид[176]. Сейчас я объясню, что значит матричный вид записи аргументов. Все нумерации неподвижных точек, которые в массиве Функции Веблена не равны нулю, можно записать с указанием их номера, при этом нумерацию позиции в массиве будем производить с правой стороны, начиная с нуля: φ("n",...,"3","2","1","0"). Так, например: φ(3,0,0,1,0,2) = φ(351220) - двойка записана на позиции номер ноль, единица записана на позиции номер два, тройка записана на позиции номер пять, нули на всех остальных позициях. Используя такой принцип, мы легко сможем переписать все имеющиеся ординалы из массивной записи в матричную, так что каждый ординал будет учтен, а значит нотация останется вполне упорядоченной.
ω = φ(1) = φ(10)
ω2 = φ(2) = φ(20)
ωω = φ(ω) = φ(ω0)
ε0 = φ(1,0) = φ(11)
ε1 = φ(1,1) = φ(1110)
ε2 = φ(1,2) = φ(1120)
εω = φ(1,ω) = φ(11ω0)
ζ0 = φ(2,0) = φ(21)
ζ1 = φ(2,1) = φ(2110)
η0 = φ(3,0) = φ(31)
η1 = φ(3,1) = φ(3110)
ωƐ0 = φ(ω,0) = φ(ω1)
ωƐ1 = φ(ω,1) = φ(ω110)
ωƐω = φ(ω,ω) = φ(ω1ω0)
Г0 = φ(1,0,0) = φ(12)
Г1 = φ(1,0,1) = φ(1210)
Г2 = φ(1,0,2) = φ(1220)
1Г0 = φ(1,1,0) = φ(2111)
1Г2 = φ(1,1,1) = φ(121110)
2Г0 = φ(1,2,0) = φ(1221)
P0 = φ(2,0,0) = φ(22)
P1 = φ(2,0,1) = φ(2201)
1Р0 = φ(2,1,0) = φ(2211)
B0 = φ(3,0,0) = φ(23)
φ(1,0,0,0) = φ(14)
φ(1,0,0,0,0) = φ(15)
φ(1,0,0,0,0,0) = φ(16)
φ(1,0,0,0,0,0,0) = φ(17)
Такие сопоставления можно проделать до ординала φ(1ω), который будет пределом массивного вида Функции Веблена и называться он будет Малым ординалом Веблена (Small Veblen ordinal)[177]. По-другому этот ординал можно назвать основная неподвижная точка ω-разряда. Достигается этот ординал как предел последовательности ординалов: φ(1), φ(1,0), φ(1,0,0), φ(1,0,0), ..., φ(1ω) = sup(1n|n<ω). Интересно то, что для каждой подфункции на любом из основых разрядов: α↦φ(α), α↦φ(α,0), α↦φ(α,0,0), α↦φ(α,0,0,0), ... данный ординал так же будет неподвижной точкой. Ну а матричный вид Функции Веблена позволяет создавать еще бо́льшие ординалы. Вторая основная неподвижная точка ω-разряда будет записана так φ(1ω10), а достигается она как sup(φ(φ(1ω)n10)|n<ω) = sup(φ(φ(1ω),1), φ(φ(1ω),0,1), φ(φ(1ω),0,0,1), ... )n<ω или так sup(φ(1nφ(1ω)+10)|n<ω) = sup(φ(φ(1ω)+1), φ(1,φ(1ω)+1), φ(1,0,φ(1ω)+1), ... )n<ω, поскольку является пределом для обоих последовательностей. Первая основная 2-неподвижная точка ω-разряда будет записана так φ(1ω11), она же первая неподвижная точка для функции α↦φ(1ωα0). Первая основная гипер-неподвижная точка ω-разряда будет записана так φ(1ω12), она же первая неподвижная точка для функции α↦φ(1ωα1). И так далее... Пока мы не получим ординал φ(2ω) = sup(1ω1n|n<ω) = sup(φ(1ω), φ(1ω11), φ(1ω12), φ(1ω13), ... )n<ω, который можно назвать 2-пределом массивного вида Функции Веблена. Тогда первая неподвижная точка α↦α-предела массивного вида Функции Веблена, или α↦φ(αω) будет записываться так φ(1ω+1), и это будет основная неподвижная точка (ω+1)-разряда. Ну а дальше, перечисляя трансфинтиные разряды основных неподвижных точек, в том числе расписывая матрицу рекурсивно: φ(1ω) = φ(1φ(10)), φ(1ε0) = φ(1φ(11)), φ(1Г0) = φ(1φ(12)), φ(1φ(1ω)) = φ(1φ(1φ(10))), φ(1φ(1φ(1ω))) = φ(1φ(1φ(1φ(10)))), мы в конце концов сможем дойти до φ(1φ(1φ(1φ(1...)))) - который и будет полным пределом матричной Функции Веблена, называться он будет Большим ординалом Веблена (Large Veblen ordinal)[177].
Здесь давайте прервем свое восхождение по ординальным нотациям, и снова разберем функцию не имеющую отношения ни к массивным нотациям ни к иерархиям от фундаментальных последовательностей ординалов, поскольку именно где-то здесь она и располагается по своей скорости роста. Функция эта опять же происходит из области теории графов связанной с теорией игр, как и Гидра Кирби-Париса. И перед тем как привести функцию, для начала следует объяснить, что значит термин "древо". А означает он следующее: древо - это такой граф, у которого имеется наличие только одного пути между любой парой узлов и отсутствуют циклы (когда узел связан сам с собой). В соответствии с этим определением, древо из одного узла без веток, тоже допустимо. Кроме того у наших деревьев могут будут разные по типу узлы, например, они могут отличаться по цвету. Теперь давайте определим игру, которая будет называться "лес", наша задача в этой игре создать лес из таких деревьев, при этом зарисовывая разные деревья по очереди, так чтобы каждое из предыдущих деревьев не было бы гомеоморфно вложенным в следующее создаваемое дерево, при этом каждое следующее дерево не может иметь в своем составе больше узлов, чем число соответствующее его порядковому номеру. Дерево называется гомеоморфно вложенным если крайние узлы и их общего предка можно отыскать в другом дереве[178]. Конечно вот так из определения сложно понять как играть в эту игру. Давайте я вначале на рисунке №57 приведу примеры гомеоморфно вложенных и гомеоморфно невложенных деревьев. Примеры нижних последовательностей деревьев с рисунка могут быть в нашем лесу, а примеры верхних последовательностей деревьев не могут входить в состав нашего леса.
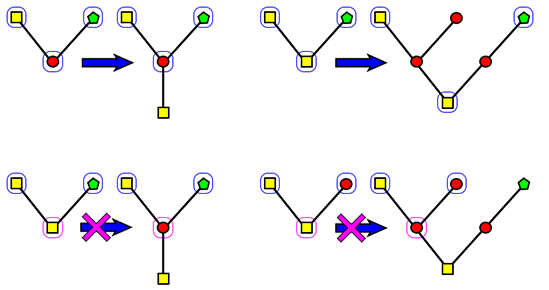
рис.57 (гомеоморфное вложение)
Теорема Краскала утверждает, что такая последовательность из создаваемых деревьев не может быть бесконечной, сколько бы разных видов узлом мы не использовали[179]. Математик Харви Фридман поставил вопрос так, а какое может быть максимальное количество деревьев в последовательности в зависимости от числа видов узлов n, создав тем самым функцию TREE(n)[180]. Давайте проверим сколько максимум деревьев мы можем посадить используя один вид узлов, то есть узнаем чему равно TREE(1). Начинаем сажать дерьевья, и так как по правилам игры, первое древо не может содержать больше одного узла, а второе больше двух узлов, получается что в единственной последовательности первое древо всегда будет вложено во второе.
рис.58
А значит в случае с одним видом узлов, наш лес может состоять только из одного дерева TREE(1) = 1.
рис.59
С двумя узлами не все так очевидно как кажется на первый взгляд. Может показаться, что единственная возможная последовательность - это если мы возьмем по одному дереву из одного узла каждое, но так чтобы узлы у них были разных видов, поскольку их нельзя вложить друг в друга.
рис.60
Ведь дальше продолжать мы не сможем, поскольку в любое возможное дерево из двух узлов, предыдущие два древа можно гомеоморфно вложить.
рис.61
Тем не менее это не самая длинная последовательность из деревьев, которую мы можем создать. Самой длинной будет вот такая:
рис.62
Легко показать, что это допустимая последовательность. Один узел нельзя вложить в древо из двух узлов другого вида, а оно в свою очередь не вкладывается в древо с одним узлом этого же вида.
рис.63
Можем поменять виды узлов в последовательности:
рис.64
Что конечно, ни коим образом, не отразиться на ее длине, поскольку виды узлов равноправны и принципы гомеоморфной вложенности останутся теми же.
рис.65
Поэтому TREE(2) = 3. Ну а дальше функция растет невероятно быстро, поскольку начиная с TREE(3) происходит настоящий взрыв[181]. Никто не сможет привести вам максимально полный лес таких деревьев, которые могут включать в себя три вида узлов. Я могу показать только начальный фрагмент последовательности:
рис.66
Всего же количество деревьев в таком лесу оценивается как TREE(3) > fφ(3ω)(n), в целом скорость роста функции начиная с этого момента становится такой[182]:
TREE(3) > fφ(3ω)(n) = fφ(3,0,0,0,0,0,0,0,...)(3)
TREE(4) > fφ(4ω)(n) = fφ(4,0,0,0,0,0,0,0,...)(4)
TREE(5) > fφ(5ω)(n) = fφ(5,0,0,0,0,0,0,0,...)(5)
TREE(6) > fφ(6ω)(n) = fφ(6,0,0,0,0,0,0,0,...)(6)
TREE(n) > fφ(ωω)(n) = fφ(ω,0,0,0,0,0,0,0,...)(n)
Ну а теперь можно снова вернуться к ординальным нотациям. Мы добрались с вами до таких огромных ординалов, рекурсии в которых столь головокружительные, что не у всех получится вот так с первого раза их осознать. Ну а если подставить их в функцию быстрорастущей иерархии, конечные числа, которые тогда будут создаваться этими функциями станут вероятно столь большими, что мы уже можем сопоставлять их со следующим расширением массивной нотации. Однако это следующее расширение столь сильное, что даже Большой ординал Веблена подставленный в функцию быстрорастущей иерархии не сможет быть сопоставим с пределом этого расширения. Поэтому нам необходима другая ординальная функция, которая будет еще сильнее чем Функция Веблена. Вникнуть в нее будет непросто, поэтому давайте подробнее разберем принципы, на которых она должна быть построена.
Вам не показалось, что Функция Веблена визуально очень похожа на массивную нотацию без расширений. Дальше следите за мыслью, чтобы сравнить рекурсии массивной нотации на конечных числах мы использовали рекурсии заложенные в трансфинитных ординалах, так что {n,n,n,n,n,...} ≈ hωωω(n) = fωω(n), при том, что предел массивной нотации использовал не весь потенциал рекурсий заложенных в ординальной нотации Кантора. При этом сами ординалы не были напрямую связаны с создаваемыми конечными числами, это был лишь хитрый трюк, мы использовали оридналы для диагоналиазции. Как мы уже знаем, правильно называть этот трюк следует словосочетанием: фундаментальная последовательность, и срабатывает она всякий раз когда в функции быстрорастущей иерархии появляется предельный ординал, который утверждает "и так бесконечное число раз", например: 1,2,3,...,ω или ω+1,ω+2,ω+3,...,ω×2 или ω,ω×2,ω×3,...,ω2, вместо этого мы заменяем это утверждение на "и так n-раз", то есть мы выбираем n-ный элемент фундаментальной последовательности ординала. Иными словами трансфинитные ординалы в функциях быстрорастущей иерархии - это диагонализаторы рекурсий на конечных числах. Так вот нам необходимы такие же диагонализаторы только для рекурсий на трансфинитных ординалах, чтобы создать более сильную ординальную нотацию. И такие диагонализаторы у нас имеются, это несчетные ординалы. Давайте вспомним, что такое несчетный ординал. Какие бы рекурсии мы не создавали на счетных одиналах, получаемый ординал все равно будет счетным, то есть это будет бесконечное множество с сильной неоднородностью, но количественно равное просто бесконечности или имеющее кардинальность ℵ0. А как мы помним из второй части, чтобы упорядочить все счетные ординалы, нам потребуется ординал лежащий за пределами этого множества: ω1 - первый несчетный ординал, имеющий кардинальность ℵ1. Этот ординал всегда будет больше любого рекурсивно-созданного счетного ординала, так же как ω - первый трансфинитный ординал больше любого конечного числа. Чуете к чему я клоню, ω1 - можно использовать как диагонализатор для создания рекурсий на счетных трансфинитных ординалах, так же как ω мы использовали как диагонализатор для создания рекурсий на конечных числах. Для создания таких диагонализаций нам тоже нужен специальный метод, аналогичный методу фундаментальных последовательностей, но работать он будет иначе, да и название у него будет другое: Ординальная коллапсирующая функция, по английски: Ordinal collapsing function (OCF).
Перед тем как разбирать эту ординальную нотацию нужно отметить, что вариаций ординальной коллапсирующей функции существует очень много, но первую версию в 1950 году создал немецкий математик Хайнц Бахман[183], в ней и был положен сам принцип, который называют Иерархией Бахмана, этот принцип используется в большинстве одних из самых сильных ординальных нотаций и мы еще не раз будем к нему прибегать. Позже было создано много разных ординальных коллапсирующих функций с увеличенными пределами. Я предлагаю для рассмотрения взять версию сформулированную в 1986 году другим немецким математиком Вильфредом Бухольцем[184], которая так и будет называться Ординальной коллапсирующей функцией Бухольца. Причем я буду разбирать здесь немного модифицированную и упрощенную другими математиками версию функции, чтобы упростить для вас ее понимание (так же я буду поступать со всем другими ординальными коллапсирующими функциями, которые появятся на страницах моей книги). Для начала, как обычно, дадим формальное определение функции.
Напомню, что данное ниже формальное определение еще не является полноценной ординальной нотацией, поскольку в нем нет алгоритма отношений принадлежности между ординалами, который, однако, легко можно найти в оригинальном труде Бухольца. Но там я привожу детально расписанные фундаментальные последовательности, на основе которых данный алгоритм так же гарантировано можно восстановить. И на этом моменте читатель может спросить, а не слишком ли много таких гарантий, которые допускают существование больших чисел, мы с вами принимаем на веру. Увы, но когда мы работаем с большими числами, мы, так или иначе, сталкиваемся с допущениями. Рекурсивный алгоритм сравнения ординалов ассоцированный с ординальной коллапсирующей функцией – это само по себе допущение, того что компьютер мог бы высчитать парсеки строк фундаментальных последовательностей, и далее конечных чисел (хотя какие парсеки, я думаю, что даже видимые вселенные будут мелковаты для этого сравнения) будь у него физические возможности, но наличие алгоритма это гарантирует. Мы вместо изучения алгоритма, предназначенного для компьютерного вычисления, лучше приведем наглядный табличный анализ иерархии ординалов со всеми рекурсивными преобразованиями, который займет у нас почти столько же места как и детальный разбор алгоритма отношений принадлежности, но для читателя анализ будет намного нагляднее.
И чтобы не быть голословным, давайте я продемонстрирую на примере Функции Веблена почему подробное разъяснение этого алгоритма сложная процедура. Если для ординальной нотации Кантора нам у двух ординалов, записанных в нормальной форме (с использованием "ω(...)", "0", "+") достаточно сравнить высоту степенной башни, при равенстве которой бо́льшим считается тот ординал, у которого на верхнем этаже бо́льший ординал, при равенстве которых следует сравнивать ординалы уже на нижних этажах, при этом на каждом этаже ординалы сравниваются по методу разложения в сумму, и если в качестве слагаемых оказываются одинаковые ординалы, то тогда сравнивается их количество на этаже. Например, ωωωω×2+ωω+1 > ωωωω+ωω×2, потому что ωωωωω0+ωωωω0+ωωω0+ω0 > ωωωωω0+ωωω0+ωω0. И если это достаточное словесное описание алгоритма отношений принадлежности, которое позволяет рекурсивно сравнить любые два ординала в нотации Кантора, то для Функции Веблена не все так однозначно. Функция одного аргумета φ(n) работает так же как нотация Кантора и для нее применим тот же алгоритм, но вот для двух и более аргументов функции возникают сложности. Казалось бы ну если, в целом, функция работает по принципу десятичной нотации, то и сравнивать можно по похожему принципу, например 312 > 231 и φ(3,1,2) > φ(2,3,1), который называется методом сравнения разрядов (для матричной записи этот метод будет расширен до сравнения разрядов с трансфинитными значениями). Однако такой алгоритм сравнения будет работать только пока мы не столкнемся с накручиванием меньших рекурсий на бо́льших ординалах, например: φ(1,φ(1,0,0)+1) = εГ0+1, но ведь такие ординалы тоже необходимо учитывать, поскольку именно с их помощью происходит достижение всех следующих неподвижных точек, которые в итоге и учитывает функция. Так что, по-хорошему, для всех видов таких промежуточных ординалов тоже должен быть определен какой-то способ сравнения, который бы изнутри переходил от бо́льших рекурсий к меньшим, попутно сравнивая их между собой. В функции Бухольца при создании алгоритма отношения принадлежности мы столкнемся с еще бо́льшим количеством подобных ситуаций (которые проявят себя уже в следующей части книги), так что детальный разбор алгоритма сравнения ординалов в итоге будет больше и сложнее наглядного анализа в виде сравнительной таблицы, именно поэтому для данной книги я выбрал второй вариант.
приложение 15 (Ординальная коллапсирующая функция Бухольца)
Теперь приступим к объяснению принципов коллапсирования. Пока я не буду подробно описывать как работает функция и разбирать формальные механизмы генерации счетных ординалов. Сам процесс коллапсирования я детально разберу в следующей части, чтобы раньше времени не перегружать читателя. Сейчас мы остановимся только на результатах функции и ее свойствах диагонализации счетных ординалов. И во-первых, обратите внимание, что ω1 - первый несчетный ординал записывается внутри коллапсирующей функции так: Ω - заглавная буква Омега. Это делается, чтобы с одной стороны запись была короче и нагляднее, чтобы счетные и несчетные ординалы явно отличались на письме, но у этого есть еще одна причина, которую я объясню позже. Сама функция записывается так: ψ(a) и в отличие от Функции Веблена принимает всего один аргумент, который может быть как конечным числом, так и счетным ординалом, так и несчетным ординалом. Если подставлять в коллапсирующую функцию конечные числа или счетные ординалы она будет работать в точности как Функция Веблена для одного аргумента φ(a) = ψ(a).
1 = φ(0) = ψ(0)
2 = φ(0)+φ(0) = ψ(0)+ψ(0)
ω = φ(1) = ψ(1)
ω×2 = φ(1)+φ(1) = ψ(1)+ψ(1)
ω2 = φ(2) = ψ(2)
ω3 = φ(3) = ψ(3)
ωω = φ(φ(1)) = ψ(ψ(1))
ωωω = φ(φ(φ(1))) = ψ(ψ(ψ(1)))
ωωωω = φ(φ(φ(φ(1)))) = ψ(ψ(ψ(ψ(1))))
ωωωω... = φ(φ(φ(φ(φ(...))))) = ψ(ψ(ψ(ψ(ψ(...)))))
Ну а дальше так же как и в Функции Веблена для одного аргумента мы сталкиваемся с неподвижной точкой и ординал ε0, подставленый в функцию вернет лишь ε0. Метод Веблена для выхода из таких ситуаций заключается в массивной нумерации неподвижных точек: ε0 = φ(1,0), ну а метод Бухольца - это использование несчетного ординала как диагонализатора ε0 = ψ(Ω). Дальше функция работает по старому принципу, только сохраняя внутри себя диагонализатор. Так же как ψ(0)+ψ(0)+ψ(0)+... = ψ(1) = ω, ψ(1)+ψ(1)+ψ(1)+... = ψ(2) = ω2, ψ(n)+ψ(n)+ψ(n)+... = ψ(n+1) = ωn+1, аналогично: ψ(Ω)+ψ(Ω)+ψ(Ω)+... = ψ(Ω+1) = ε0+ε0+ε0+... = ε0×ω = ωε0+1, ψ(Ω+1)+ψ(Ω+1)+ψ(Ω+1)+... = ψ(Ω+2) = ε0×ω×ω = ωε0+2, ψ(Ω+n) = ωε0+n. После чего мы можем записать уже такое выражение: ψ(Ω+ψ(Ω)) = ψ(Ω+ε0) = ωε0+ε0 = ωε0×2, затем продолжим в таком же духе: ψ(Ω+ψ(Ω+ψ(Ω))) = ωωε0×2, ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)))) = ωωωε0×2 и в конечном счете доберемся до второй неподвижной точки α↦ωα = ε1 = φ(1,1) = ψ(Ω+ψ(Ω+ψ(Ω+ψ(...)))). А это уже служит поводом для новой диагонализации: ψ(Ω+ψ(Ω+ψ(Ω+ψ(...)))) = ψ(Ω+Ω) = ψ(Ω×2). Заметьте одну важную деталь: Ω+ψ(Ω+ψ(Ω+ψ(...))) ≠ Ω+Ω, мы не можем достать диагонализатор из функции и делать с ним те же преобразования, поскольку Ω мы определили как первый несчетный ординал и сколько не складывай с ним счетные ординалы все равно не получишь Ω+Ω. Подобные преобразования можно делать только внутри функции, соответствия в которой могут быть определены произвольным способом. Соответствия коллапсирующей функции же приводят нас к тому, что количество Ω внутри функции учитывает номера неподвижных точек α↦ωα. Следовательно, мы получаем, что ψ(Ω×n) = εn-1 = φ(1,n-1), если n < ω и ψ(Ω×n) = εn = φ(1,n), если n ≥ ω. И тогда уже ψ(Ω×ψ(Ω)) = ψ(Ω×ε0) = εε0, ну и далее ψ(Ω×ψ(Ω×ψ(Ω))) = εεε0. А значит следующей диагонализацией будет: ζ0 = εεεε... = φ(2,0) = ψ(Ω+ψ(Ω+ψ(Ω+ψ(...)))) = ψ(Ω×Ω) = ψ(Ω2), что будет дважды неподвижной точкой α↦ωα. Здесь работает та же логика, диагонализатор нельзя доставать из функции: Ω×ψ(Ω×ψ(Ω×ψ(...))) ≠ Ω×Ω, потому что аналогично операции сложения, сколько не умножай несчетный ординал со счетными ординалами все равно не получишь Ω×Ω. Однако внутри функции определено, что ψ(Ωn) будет учитывать n-неподвижные точки α↦ωα. Так что в общем случае: ψ(Ωn) = φ(n,0), и мы снова имеем прецедент для новой диагонализации: ψ(ΩΩ) = ψ(Ωψ(Ωψ(Ωψ(Ωψ(...))))) = Г0 = φ(1,0,0), она же первая гипер-неподвижная точка α↦ωα.
Здесь давайте остановимся и обратим внимание на одну интересную деталь, помните как ωω был PTO для PRA или RCA0, то есть с использованием ωω можно было создать рекурсию, которая была бы сильнее любой примитивно-рекурсивной функции на конечных числах, такие функции еще называют ограничено квантифицированными (далее я объясню, что это значит). Так вот ψ(ΩΩ) = Г0 является PTO для ATR0, то есть с использованием ψ(ΩΩ) можно создать рекурсию, которая будет сильнее рекурсии созданной с помощью ограничено квантифицированной рекурсии на трансфинитных ординалах, и это не просто совпадение, а естественная иерархическая преемственность.
Ну а мы на основе коллапсирования можем продолжать создавать диагонализации и дальше. Поскольку степенные башни могут предоставить нам великое множество операций на несчетном ординале, то и возможностей для диагонализации высших неподвижных точек α↦ωα, так же будет великое множество. Например: ψ(ΩΩ×k+m×n) будет учитывать n-ные m-гиперk-неподвижные точки α↦ωα или, что тоже самое: φ(k,m,n). Ну а ψ(ΩΩn) будет уже учитывать основные неподвижные точки (n+1)-ого разряда, если n < ω; и n-ого разряда, если n ≥ ω; по полной задействуя при сравнении Функцию Веблена. Тогда уже диагонализация на этих разрядах будет соответствовать ψ(ΩΩψ(ΩΩψ(ΩΩ...))) = ψ(ΩΩΩ), что является Большим ординалом Веблена, а значит это доказывает, что Иерархия Бахмана сильнее Иерархии Веблена и для выражения больших ординалов мы теперь будем пользоваться ординальной коллапсирующей функцией. Однако сперва для полного и детального понимания я приведу такую же большую сравнительную таблицу, которую приводил для сравнения нотации Кантора и Функции Вебелна, только теперь мы добавим туда еще Ординальную коллапсирующую функцию Бухольца.
| ε0 |
φ(1,0) = φ(φ(φ(φ(φ(φ(φ(φ(...)))))))) |
ψ(Ω) = ψ(ψ(ψ(ψ(ψ(ψ(ψ(ψ(...)))))))) |
| ε0+1 |
φ(1,0)+φ(0) |
ψ(Ω)+ψ(0) |
| ε0+2 |
φ(1,0)+φ(0)+φ(0) |
ψ(Ω)+ψ(0)+ψ(0) |
| ε0+3 |
φ(1,0)+φ(0)+φ(0)+φ(0) |
ψ(Ω)+ψ(0)+ψ(0)+ψ(0) |
| ε0+ω |
φ(1,0)+φ(1) = φ(1,0)+φ(0)+φ(0)+φ(0)+... |
ψ(Ω)+ψ(1) = ψ(Ω)+ψ(0)+ψ(0)+ψ(0)+... |
| ε0+ω+1 |
φ(1,0)+φ(1)+φ(0) |
ψ(Ω)+ψ(1)+ψ(0) |
| ε0+ω×2 |
φ(1,0)+φ(1)+φ(1) |
ψ(Ω)+ψ(1)+ψ(1) |
| ε0+ω2 |
φ(1,0)+φ(2) |
ψ(Ω)+ψ(2) |
| ε0+ω2+1 |
φ(1,0)+φ(2)+φ(0) |
ψ(Ω)+ψ(2)+ψ(0) |
| ε0+ω2+ω |
φ(1,0)+φ(2)+φ(1) |
ψ(Ω)+ψ(2)+ψ(1) |
| ε0+ω2×2 |
φ(1,0)+φ(2)+φ(2) |
ψ(Ω)+ψ(2)+ψ(2) |
| ε0+ω3 |
φ(1,0)+φ(3) |
ψ(Ω)+ψ(3) |
| ε0+ωω |
φ(1,0)+φ(φ(1)) |
ψ(Ω)+ψ(ψ(1)) |
| ε0+ωω+1 |
φ(1,0)+φ(φ(1))+φ(0) |
ψ(Ω)+ψ(ψ(1))+ψ(0) |
| ε0+ωω+ω |
φ(1,0)+φ(φ(1))+φ(1) |
ψ(Ω)+ψ(ψ(1))+ψ(1) |
| ε0+ωω+ω2 |
φ(1,0)+φ(φ(1))+φ(2) |
ψ(Ω)+ψ(ψ(1))+ψ(2) |
| ε0+ωω×2 |
φ(1,0)+φ(φ(1))+φ(φ(1)) |
ψ(Ω)+ψ(ψ(1))+ψ(ψ(1)) |
| ε0+ωω+1 |
φ(1,0)+φ(φ(1)+φ(0)) |
ψ(Ω)+ψ(ψ(1)+ψ(0)) |
| ε0+ωω+1+1 |
φ(1,0)+φ(φ(1)+φ(0))+φ(0) |
ψ(Ω)+ψ(ψ(1)+ψ(0))+ψ(0) |
| ε0+ωω+1+ωω |
φ(1,0)+φ(φ(1)+φ(0))+φ(φ(1)) |
ψ(Ω)+ψ(ψ(1)+ψ(0))+ψ(ψ(1)) |
| ε0+ωω+1×2 |
φ(1,0)+φ(φ(1)+φ(0))+φ(φ(1)+φ(0)) |
ψ(Ω)+ψ(ψ(1)+ψ(0))+ψ(ψ(1)+ψ(0)) |
| ε0+ωω+2 |
φ(1,0)+φ(φ(1)+φ(0)+φ(0)) |
ψ(Ω)+ψ(ψ(1)+ψ(0)+ψ(0)) |
| ε0+ωω×2 |
φ(1,0)+φ(φ(1)+φ(1)) |
ψ(Ω)+ψ(ψ(1)+ψ(1)) |
| ε0+ωω×3 |
φ(1,0)+φ(φ(1)+φ(1)+φ(1)) |
ψ(Ω)+ψ(ψ(1)+ψ(1)+ψ(1)) |
| ε0+ωω2 |
φ(1,0)+φ(φ(2)) |
ψ(Ω)+ψ(ψ(2)) |
| ε0+ωω3 |
φ(1,0)+φ(φ(3)) |
ψ(Ω)+ψ(ψ(3)) |
| ε0+ωωω |
φ(1,0)+φ(φ(φ(1))) |
ψ(Ω)+ψ(ψ(ψ(1))) |
| ε0+ωωω+1 |
φ(1,0)+φ(φ(φ(1)))+φ(0) |
ψ(Ω)+ψ(ψ(ψ(1)))+ψ(0) |
| ε0+ωωω+1 |
φ(1,0)+φ(φ(φ(1))+φ(0)) |
ψ(Ω)+ψ(ψ(ψ(1))+ψ(0)) |
| ε0+ωωω+1 |
φ(1,0)+φ(φ(φ(1)+φ(0))) |
ψ(Ω)+ψ(ψ(ψ(1)+ψ(0))) |
| ε0+ωωω×2 |
φ(1,0)+φ(φ(φ(1)+φ(1))) |
ψ(Ω)+ψ(ψ(ψ(1)+ψ(1))) |
| ε0+ωωω2 |
φ(1,0)+φ(φ(φ(2))) |
ψ(Ω)+ψ(ψ(ψ(2))) |
| ε0+ωωω3 |
φ(1,0)+φ(φ(φ(3))) |
ψ(Ω)+ψ(ψ(ψ(3))) |
| ε0+ωωωω |
φ(1,0)+φ(φ(φ(φ(1)))) |
ψ(Ω)+ψ(ψ(ψ(ψ(1)))) |
| ε0+ωωωω+1 |
φ(1,0)+φ(φ(φ(φ(1))))+φ(0) |
ψ(Ω)+ψ(ψ(ψ(ψ(1))))+ψ(0) |
| ε0+ωωωω+1 |
φ(1,0)+φ(φ(φ(φ(1)))+φ(0)) |
ψ(Ω)+ψ(ψ(ψ(ψ(1)))+ψ(0)) |
| ε0+ωωωω+1 |
φ(1,0)+φ(φ(φ(φ(1))+φ(0))) |
ψ(Ω)+ψ(ψ(ψ(ψ(1))+ψ(0))) |
| ε0+ωωωω+ω |
φ(1,0)+φ(φ(φ(φ(1))+φ(1))) |
ψ(Ω)+ψ(ψ(ψ(ψ(1))+ψ(1))) |
| ε0+ωωωω×2 |
φ(1,0)+φ(φ(φ(φ(1))+φ(φ(1)))) |
ψ(Ω)+ψ(ψ(ψ(ψ(1))+ψ(ψ(1)))) |
| ε0+ωωωω+1 |
φ(1,0)+φ(φ(φ(φ(1)+φ(0)))) |
ψ(Ω)+ψ(ψ(ψ(ψ(1)+ψ(0)))) |
| ε0+ωωωω×2 |
φ(1,0)+φ(φ(φ(φ(1)+φ(1)))) |
ψ(Ω)+ψ(ψ(ψ(ψ(1)+ψ(1)))) |
| ε0+ωωωω2 |
φ(1,0)+φ(φ(φ(φ(2)))) |
ψ(Ω)+ψ(ψ(ψ(ψ(2)))) |
| ε0+ωωωωω |
φ(1,0)+φ(φ(φ(φ(φ(1))))) |
ψ(Ω)+ψ(ψ(ψ(ψ(ψ(1))))) |
| ε0+ωωωωωω |
φ(1,0)+φ(φ(φ(φ(φ(φ(1)))))) |
ψ(Ω)+ψ(ψ(ψ(ψ(ψ(ψ(1)))))) |
| ε0×2 |
φ(1,0)+φ(φ(φ(...))) = φ(1,0)+φ(1,0) |
ψ(Ω)+ψ(ψ(ψ(...))) = ψ(Ω)+ψ(Ω) |
| ε0×2+1 |
φ(1,0)+φ(1,0)+φ(0) |
ψ(Ω)+ψ(Ω)+ψ(0) |
| ε0×2+ω |
φ(1,0)+φ(1,0)+φ(1) |
ψ(Ω)+ψ(Ω)+ψ(1) |
| ε0×2+ωω |
φ(1,0)+φ(1,0)+φ(φ(1)) |
ψ(Ω)+ψ(Ω)+ψ(ψ(1)) |
| ε0×2+ωωω |
φ(1,0)+φ(1,0)+φ(φ(φ(1))) |
ψ(Ω)+ψ(Ω)+ψ(ψ(ψ(1))) |
| ε0×2+ωωωω |
φ(1,0)+φ(1,0)+φ(φ(φ(φ(1)))) |
ψ(Ω)+ψ(Ω)+ψ(ψ(ψ(ψ(1)))) |
| ε0×3 |
φ(1,0)+φ(1,0)+φ(1,0) |
ψ(Ω)+ψ(Ω)+ψ(Ω) |
| ε0×4 |
φ(1,0)+φ(1,0)+φ(1,0)+φ(1,0) |
ψ(Ω)+ψ(Ω)+ψ(Ω)+ψ(Ω) |
| ωε0+1 |
φ(φ(1,0)+1) = φ(1,0)+φ(1,0)+φ(1,0)+... |
ψ(Ω+ψ(0)) = ψ(Ω+1) = ψ(Ω)+ψ(Ω)+ψ(Ω)+... |
| ωε0+1+ε0 |
φ(φ(1,0)+1)+φ(1,0) |
ψ(Ω+1)+ψ(Ω) |
| ωε0+1×2 |
φ(φ(1,0)+1)+φ(φ(1,0)+1) |
ψ(Ω+1)+ψ(Ω+1) |
| ωε0+2 |
φ(φ(1,0)+2) = φ(φ(1,0)+1)+φ(φ(1,0)+1)+... |
ψ(Ω+ψ(0)+ψ(0)) = ψ(Ω+2) = ψ(Ω+1)+ψ(Ω+1)+... |
| ωε0+3 |
φ(φ(1,0)+3) = φ(φ(1,0)+2)+φ(φ(1,0)+2)+... |
ψ(Ω+ψ(0)+ψ(0)+ψ(0)) = ψ(Ω+3) = ψ(Ω+2)+ψ(Ω+2)+... |
| ωε0+ω |
φ(φ(1,0)+φ(1)) |
ψ(Ω+ψ(1)) = ψ(Ω+ω) |
| ωε0+ω+ε0 |
φ(φ(1,0)+φ(1))+φ(1,0) |
ψ(Ω+ω)+ψ(Ω) |
| ωε0+ω+ωε0+1 |
φ(φ(1,0)+φ(1))+φ(φ(1,0)+1) |
ψ(Ω+ω)+ψ(Ω+1) |
| ωε0+ω×2 |
φ(φ(1,0)+φ(1))+φ(φ(1,0)+φ(1)) |
ψ(Ω+ω)+ψ(Ω+ω) |
| ωε0+ω+1 |
φ(φ(1,0)+φ(1)+1) |
ψ(Ω+ψ(1)+ψ(0)) = ψ(Ω+ω+1) |
| ωε0+ω×2 |
φ(φ(1,0)+φ(1)+φ(1)) |
ψ(Ω+ψ(1)+ψ(1)) = ψ(Ω+ω+ω) |
| ωε0+ω2 |
φ(φ(1,0)+φ(2)) |
ψ(Ω+ψ(2)) = ψ(Ω+ω2) |
| ωε0+ωω |
φ(φ(1,0)+φ(φ(1))) |
ψ(Ω+ψ(ψ(1))) = ψ(Ω+ωω) |
| ωε0+ωωω |
φ(φ(1,0)+φ(φ(φ(1)))) |
ψ(Ω+ψ(ψ(ψ(1)))) = ψ(Ω+ωωω) |
| ωε0+ωωωω |
φ(φ(1,0)+φ(φ(φ(φ(1))))) |
ψ(Ω+ψ(ψ(ψ(ψ(1))))) = ψ(Ω+ωωωω) |
| ωε0×2 |
φ(φ(1,0)+φ(1,0)) |
ψ(Ω+ψ(Ω)) |
| ωε0×2×2 |
φ(φ(1,0)+φ(1,0))+φ(φ(1,0)+φ(1,0)) |
ψ(Ω+ψ(Ω))+ψ(Ω+ψ(Ω)) |
| ωε0×2+1 |
φ(φ(1,0)+φ(1,0)+1) |
ψ(Ω+ψ(Ω)+1) |
| ωε0×2+ω |
φ(φ(1,0)+φ(1,0)+φ(1)) |
ψ(Ω+ψ(Ω)+ψ(1)) |
| ωε0×2+ωω |
φ(φ(1,0)+φ(1,0)+φ(φ(1))) |
ψ(Ω+ψ(Ω)+ψ(ψ(1))) |
| ωε0×2+ωωω |
φ(φ(1,0)+φ(1,0)+φ(φ(φ(1)))) |
ψ(Ω+ψ(Ω)+ψ(ψ(ψ(1)))) |
| ωε0×3 |
φ(φ(1,0)+φ(1,0)+φ(1,0)) |
ψ(Ω+ψ(Ω)+ψ(Ω)) |
| ωωε0+1 |
φ(φ(φ(1,0)+1)) = φ(φ(1,0)+φ(1,0)+φ(1,0)+...) |
ψ(Ω+ψ(Ω+1)) = ψ(Ω+ψ(Ω)+ψ(Ω)+ψ(Ω)+...) |
| ωωε0+1+1 |
φ(φ(φ(1,0)+1))+1 |
ψ(Ω+ψ(Ω+1))+1 |
| ωωε0+1+ω |
φ(φ(φ(1,0)+1))+φ(1) |
ψ(Ω+ψ(Ω+1))+ψ(1) |
| ωωε0+1+ωω |
φ(φ(φ(1,0)+1))+φ(φ(1)) |
ψ(Ω+ψ(Ω+1))+ψ(ψ(1)) |
| ωωε0+1+ε0 |
φ(φ(φ(1,0)+1))+φ(1,0) |
ψ(Ω+ψ(Ω+1))+ψ(Ω) |
| ωωε0+1+ε0×2 |
φ(φ(φ(1,0)+1))+φ(1,0)+φ(1,0) |
ψ(Ω+ψ(Ω+1))+ψ(Ω)+ψ(Ω) |
| ωωε0+1+ωε0+1 |
φ(φ(φ(1,0)+1))+φ(φ(1,0)+1) |
ψ(Ω+ψ(Ω+1))+ψ(Ω+1) |
| ωωε0+1+ωε0+ω |
φ(φ(φ(1,0)+1))+φ(φ(1,0)+φ(1)) |
ψ(Ω+ψ(Ω+1))+ψ(Ω+ψ(1)) |
| ωωε0+1+ωε0×2 |
φ(φ(φ(1,0)+1))+φ(φ(1,0)+φ(1,0)) |
ψ(Ω+ψ(Ω+1))+ψ(Ω+ψ(Ω)) |
| ωωε0+1×2 |
φ(φ(φ(1,0)+1))+φ(φ(φ(1,0)+1)) |
ψ(Ω+ψ(Ω+1))+ψ(Ω+ψ(Ω+1)) |
| ωωε0+1+1 |
φ(φ(φ(1,0)+1)+1) |
ψ(Ω+ψ(Ω+1)+1) |
| ωωε0+1+ω |
φ(φ(φ(1,0)+1)+φ(1)) |
ψ(Ω+ψ(Ω+1)+ψ(1)) |
| ωωε0+1+ε0 |
φ(φ(φ(1,0)+1)+φ(1,0)) |
ψ(Ω+ψ(Ω+1)+ψ(Ω)) |
| ωωε0+1+ε0+1 |
φ(φ(φ(1,0)+1)+φ(1,0)+1) |
ψ(Ω+ψ(Ω+1)+ψ(Ω)+1) |
| ωωε0+1+ε0+ε0 |
φ(φ(φ(1,0)+1)+φ(1,0)+φ(1,0)) |
ψ(Ω+ψ(Ω+1)+ψ(Ω)+ψ(Ω)) |
| ωωε0+1×2 |
φ(φ(φ(1,0)+1)+φ(φ(1,0)+1)) |
ψ(Ω+ψ(Ω+1)+ψ(Ω+1)) |
| ωωε0+1×3 |
φ(φ(φ(1,0)+1)+φ(φ(1,0)+1)+φ(φ(1,0)+1)) |
ψ(Ω+ψ(Ω+1)+ψ(Ω+1)+ψ(Ω+1)) |
| ωωε0+2 |
φ(φ(φ(1,0)+2)) |
ψ(Ω+ψ(Ω+2)) |
| ωωε0+ω |
φ(φ(φ(1,0)+φ(1))) |
ψ(Ω+ψ(Ω+ψ(1))) |
| ωωε0+ω+1 |
φ(φ(φ(1,0)+φ(1)+1)) |
ψ(Ω+ψ(Ω+ψ(1)+1)) |
| ωωε0+ω×2 |
φ(φ(φ(1,0)+φ(1)+φ(1))) |
ψ(Ω+ψ(Ω+ψ(1)+ψ(1))) |
| ωωε0+ω2 |
φ(φ(φ(1,0)+φ(2))) |
ψ(Ω+ψ(Ω+ψ(2))) |
| ωωε0+ω2+1 |
φ(φ(φ(1,0)+φ(2)+1)) |
ψ(Ω+ψ(Ω+ψ(2)+1)) |
| ωωε0+ω2+ω |
φ(φ(φ(1,0)+φ(2)+φ(1))) |
ψ(Ω+ψ(Ω+ψ(2)+ψ(1))) |
| ωωε0+ω2×2 |
φ(φ(φ(1,0)+φ(2)+φ(2))) |
ψ(Ω+ψ(Ω+ψ(2)+ψ(2))) |
| ωωε0+ω3 |
φ(φ(φ(1,0)+φ(3))) |
ψ(Ω+ψ(Ω+ψ(3))) |
| ωωε0+ωω |
φ(φ(φ(1,0)+φ(φ(1)))) |
ψ(Ω+ψ(Ω+ψ(ψ(1)))) |
| ωωε0+ωω+1 |
φ(φ(φ(1,0)+φ(φ(1))+1)) |
ψ(Ω+ψ(Ω+ψ(ψ(1))+1)) |
| ωωε0+ωω+ω |
φ(φ(φ(1,0)+φ(φ(1))+φ(1))) |
ψ(Ω+ψ(Ω+ψ(ψ(1))+ψ(1))) |
| ωωε0+ωω+ω2 |
φ(φ(φ(1,0)+φ(φ(1))+φ(2))) |
ψ(Ω+ψ(Ω+ψ(ψ(1))+ψ(2))) |
| ωωε0+ωω×2 |
φ(φ(φ(1,0)+φ(φ(1))+φ(φ(1)))) |
ψ(Ω+ψ(Ω+ψ(ψ(1))+ψ(ψ(1)))) |
| ωωε0+ωω+1 |
φ(φ(φ(1,0)+φ(φ(1)+1))) |
ψ(Ω+ψ(Ω+ψ(ψ(1)+1))) |
| ωωε0+ωω+1+1 |
φ(φ(φ(1,0)+φ(φ(1)+1)+1)) |
ψ(Ω+ψ(Ω+ψ(ψ(1)+1)+1)) |
| ωωε0+ωω+1+ωω |
φ(φ(φ(1,0)+φ(φ(1)+1)+φ(φ(1)))) |
ψ(Ω+ψ(Ω+ψ(ψ(1)+1)+ψ(ψ(1)))) |
| ωωε0+ωω+1×2 |
φ(φ(φ(1,0)+φ(φ(1)+1)+φ(φ(1)+1))) |
ψ(Ω+ψ(Ω+ψ(ψ(1)+1)+ψ(ψ(1)+1))) |
| ωωε0+ωω+2 |
φ(φ(φ(1,0)+φ(φ(1)+2))) |
ψ(Ω+ψ(Ω+ψ(ψ(1)+2))) |
| ωωε0+ωω×2 |
φ(φ(φ(1,0)+φ(φ(1)+φ(1)))) |
ψ(Ω+ψ(Ω+ψ(ψ(1)+ψ(1)))) |
| ωωε0+ωω×3 |
φ(φ(φ(1,0)+φ(φ(1)+φ(1)+φ(1)))) |
ψ(Ω+ψ(Ω+ψ(ψ(1)+ψ(1)+ψ(1)))) |
| ωωε0+ωω2 |
φ(φ(φ(1,0)+φ(φ(2)))) |
ψ(Ω+ψ(Ω+ψ(ψ(2)))) |
| ωωε0+ωω3 |
φ(φ(φ(1,0)+φ(φ(3)))) |
ψ(Ω+ψ(Ω+ψ(ψ(3)))) |
| ωωε0+ωωω |
φ(φ(φ(1,0)+φ(φ(φ(1))))) |
ψ(Ω+ψ(Ω+ψ(ψ(ψ(1))))) |
| ωωε0+ωωω+1 |
φ(φ(φ(1,0)+φ(φ(φ(1)+1)))) |
ψ(Ω+ψ(Ω+ψ(ψ(ψ(1)+1)))) |
| ωωε0+ωωω×2 |
φ(φ(φ(1,0)+φ(φ(φ(1)+φ(1))))) |
ψ(Ω+ψ(Ω+ψ(ψ(ψ(1)+ψ(1))))) |
| ωωε0+ωωω2 |
φ(φ(φ(1,0)+φ(φ(φ(2))))) |
ψ(Ω+ψ(Ω+ψ(ψ(ψ(2))))) |
| ωωε0+ωωω3 |
φ(φ(φ(1,0)+φ(φ(φ(3))))) |
ψ(Ω+ψ(Ω+ψ(ψ(ψ(3))))) |
| ωωε0+ωωωω |
φ(φ(φ(1,0)+φ(φ(φ(φ(1)))))) |
ψ(Ω+ψ(Ω+ψ(ψ(ψ(ψ(1)))))) |
| ωωε0×2 |
φ(φ(φ(1,0)+φ(1,0))) |
ψ(Ω+ψ(Ω+ψ(Ω))) |
| ωωε0×2+1 |
φ(φ(φ(1,0)+φ(1,0)))+1 |
ψ(Ω+ψ(Ω+ψ(Ω)))+1 |
| ωωε0×2+ε0 |
φ(φ(φ(1,0)+φ(1,0)))+φ(1,0) |
ψ(Ω+ψ(Ω+ψ(Ω)))+ψ(Ω) |
| ωωε0×2+ωωε0+1 |
φ(φ(φ(1,0)+φ(1,0)))+φ(φ(φ(1,0)+1)) |
ψ(Ω+ψ(Ω+ψ(Ω)))+ψ(Ω+ψ(Ω+1)) |
| ωωε0×2×2 |
φ(φ(φ(1,0)+φ(1,0)))+φ(φ(φ(1,0)+φ(1,0))) |
ψ(Ω+ψ(Ω+ψ(Ω)))+ψ(Ω+ψ(Ω+ψ(Ω))) |
| ωωε0×2+1 |
φ(φ(φ(1,0)+φ(1,0))+1) |
ψ(Ω+ψ(Ω+ψ(Ω))+1) |
| ωωε0×2+ε0 |
φ(φ(φ(1,0)+φ(1,0))+φ(1,0)) |
ψ(Ω+ψ(Ω+ψ(Ω))+ψ(Ω)) |
| ωωε0×2+ωε0+1 |
φ(φ(φ(1,0)+φ(1,0))+φ(φ(1,0)+1)) |
ψ(Ω+ψ(Ω+ψ(Ω))+ψ(Ω+1)) |
| ωωε0×2×2 |
φ(φ(φ(1,0)+φ(1,0))+φ(φ(1,0)+φ(1,0))) |
ψ(Ω+ψ(Ω+ψ(Ω))+ψ(Ω+ψ(Ω))) |
| ωωε0×2+1 |
φ(φ(φ(1,0)+φ(1,0)+1)) |
ψ(Ω+ψ(Ω+ψ(Ω)+1)) |
| ωωε0×2+ω |
φ(φ(φ(1,0)+φ(1,0)+φ(1))) |
ψ(Ω+ψ(Ω+ψ(Ω)+ψ(1))) |
| ωωε0×2+ωω |
φ(φ(φ(1,0)+φ(1,0)+φ(φ(1)))) |
ψ(Ω+ψ(Ω+ψ(Ω)+ψ(ψ(1)))) |
| ωωε0×3 |
φ(φ(φ(1,0)+φ(1,0)+φ(1,0))) |
ψ(Ω+ψ(Ω+ψ(Ω)+ψ(Ω))) |
| ωωε0×4 |
φ(φ(φ(1,0)+φ(1,0)+φ(1,0)+φ(1,0))) |
ψ(Ω+ψ(Ω+ψ(Ω)+ψ(Ω)+ψ(Ω))) |
| ωωωε0+1 |
φ(φ(φ(φ(1,0)+1))) |
ψ(Ω+ψ(Ω+ψ(Ω+1))) |
| ωωωε0+1+ε0 |
φ(φ(φ(φ(1,0)+1)+φ(1,0))) |
ψ(Ω+ψ(Ω+ψ(Ω+1)+ψ(Ω))) |
| ωωωε0+1×2 |
φ(φ(φ(φ(1,0)+1)+φ(φ(1,0)+1))) |
ψ(Ω+ψ(Ω+ψ(Ω+1)+ψ(Ω+1))) |
| ωωωε0+2 |
φ(φ(φ(φ(1,0)+2))) |
ψ(Ω+ψ(Ω+ψ(Ω+2))) |
| ωωωε0+ω |
φ(φ(φ(φ(1,0)+φ(1)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(1)))) |
| ωωωε0+ω+ε0 |
φ(φ(φ(φ(1,0)+φ(1))+φ(1,0))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(1))+ψ(Ω))) |
| ωωωε0+ω×2 |
φ(φ(φ(φ(1,0)+φ(1))+φ(φ(1,0)+φ(1)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(1))+ψ(Ω+ψ(1)))) |
| ωωωε0+ω+1 |
φ(φ(φ(φ(1,0)+φ(1)+1))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(1)+1))) |
| ωωωε0+ω×2 |
φ(φ(φ(φ(1,0)+φ(1)+φ(1)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(1)+ψ(1)))) |
| ωωωε0+ω2 |
φ(φ(φ(φ(1,0)+φ(2)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(2)))) |
| ωωωε0+ωω |
φ(φ(φ(φ(1,0)+φ(φ(1))))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(ψ(1))))) |
| ωωωε0×2 |
φ(φ(φ(φ(1,0)+φ(1,0)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)))) |
| ωωωε0×2×2 |
φ(φ(φ(φ(1,0)+φ(1,0))+φ(φ(1,0)+φ(1,0)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω))+ψ(Ω+ψ(Ω)))) |
| ωωωε0×2+1 |
φ(φ(φ(φ(1,0)+φ(1,0)+1))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)+1))) |
| ωωωε0×2+ω |
φ(φ(φ(φ(1,0)+φ(1,0)+φ(1)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)+ψ(1)))) |
| ωωωε0×2+ωω |
φ(φ(φ(φ(1,0)+φ(1,0)+φ(φ(1))))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)+ψ(ψ(1))))) |
| ωωωε0×3 |
φ(φ(φ(φ(1,0)+φ(1,0)+φ(1,0)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)+ψ(Ω)))) |
| ωωωωε0+1 |
φ(φ(φ(φ(φ(1,0)+1)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1)))) |
| ωωωωε0+1+ε0 |
φ(φ(φ(φ(φ(1,0)+1))+φ(1,0))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1))+ψ(Ω))) |
| ωωωωε0+1+ε0×2 |
φ(φ(φ(φ(φ(1,0)+1))+φ(1,0)+φ(1,0))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1))+ψ(Ω)+ψ(Ω))) |
| ωωωωε0+1+ωε0+1 |
φ(φ(φ(φ(φ(1,0)+1))+φ(φ(1,0)+1))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1))+ψ(Ω+1))) |
| ωωωωε0+1+ωε0×2 |
φ(φ(φ(φ(φ(1,0)+1))+φ(φ(1,0)+φ(1,0)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1))+ψ(Ω+ψ(Ω)))) |
| ωωωωε0+1×2 |
φ(φ(φ(φ(φ(1,0)+1))+φ(φ(φ(1,0)+1)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1))+ψ(Ω+ψ(Ω+1)))) |
| ωωωωε0+1+1 |
φ(φ(φ(φ(φ(1,0)+1)+1))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1)+1))) |
| ωωωωε0+1+ε0 |
φ(φ(φ(φ(φ(1,0)+1)+φ(1,0)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1)+ψ(Ω)))) |
| ωωωωε0+1+ε0+1 |
φ(φ(φ(φ(φ(1,0)+1)+φ(1,0)+1))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1)+ψ(Ω)+1))) |
| ωωωωε0+1+ε0×2 |
φ(φ(φ(φ(φ(1,0)+1)+φ(1,0)+φ(1,0)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1)+ψ(Ω)+ψ(Ω)))) |
| ωωωωε0+1×2 |
φ(φ(φ(φ(φ(1,0)+1)+φ(φ(1,0)+1)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1)+ψ(Ω+1)))) |
| ωωωωε0+2 |
φ(φ(φ(φ(φ(1,0)+2)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+2)))) |
| ωωωωε0+3 |
φ(φ(φ(φ(φ(1,0)+3)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+3)))) |
| ωωωωε0+ω |
φ(φ(φ(φ(φ(1,0)+φ(1))))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(1))))) |
| ωωωωε0+ωω |
φ(φ(φ(φ(φ(1,0)+φ(φ(1)))))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(ψ(1)))))) |
| ωωωωε0×2 |
φ(φ(φ(φ(φ(1,0)+φ(1,0))))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω))))) |
| ωωωωε0×2+1 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)))+1)) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)))+1)) |
| ωωωωε0×2+ε0 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)))+φ(1,0))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)))+ψ(Ω))) |
| ωωωωε0×2+ωε0+1 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)))+φ(φ(1,0)+1))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)))+ψ(Ω+1))) |
| ωωωωε0×2+ωε0×2 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)))+φ(φ(1,0)+φ(1,0)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)))+ψ(Ω+ψ(Ω)))) |
| ωωωωε0×2+ωωε0+1 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)))+φ(φ(φ(1,0)+1)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)))+ψ(Ω+ψ(Ω+1)))) |
| ωωωωε0×2×2 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)))+φ(φ(φ(1,0)+φ(1,0))))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)))+ψ(Ω+ψ(Ω+ψ(Ω))))) |
| ωωωωε0×2+1 |
φ(φ(φ(φ(φ(1,0)+φ(1,0))+1))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω))+1))) |
| ωωωωε0×2+ε0 |
φ(φ(φ(φ(φ(1,0)+φ(1,0))+φ(1,0)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω))+ψ(Ω)))) |
| ωωωωε0×2×2 |
φ(φ(φ(φ(φ(1,0)+φ(1,0))+φ(φ(1,0)+φ(1,0))))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω))+ψ(Ω+ψ(Ω))))) |
| ωωωωε0×2+1 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)+1)))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)+1)))) |
| ωωωωε0×2+ω |
φ(φ(φ(φ(φ(1,0)+φ(1,0)+φ(1))))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)+ψ(1))))) |
| ωωωωε0×3 |
φ(φ(φ(φ(φ(1,0)+φ(1,0)+φ(1,0))))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)+ψ(Ω))))) |
| ωωωωωε0+1 |
φ(φ(φ(φ(φ(φ(1,0)+1))))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1))))) |
| ωωωωωε0×2 |
φ(φ(φ(φ(φ(φ(1,0)+φ(1,0)))))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)))))) |
| ωωωωωωε0+1 |
φ(φ(φ(φ(φ(φ(φ(1,0)+1)))))) |
ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1)))))) |
| ε1 |
φ(1,1) = φ(φ(φ(φ(...φ(1,0)+1...)))) |
ψ(Ω×2) = ψ(Ω+Ω) = ψ(Ω+ψ(Ω+ψ(Ω+ψ(...)))) |
| ε1+1 |
φ(1,1)+1 |
ψ(Ω×2)+1 |
| ε1+ω |
φ(1,1)+φ(1) |
ψ(Ω×2)+ψ(1) |
| ε1+ωω |
φ(1,1)+φ(φ(1)) |
ψ(Ω×2)+ψ(ψ(1)) |
| ε1+ε0 |
φ(1,1)+φ(1,0) |
ψ(Ω×2)+ψ(Ω) |
| ε1×2 |
φ(1,1)+φ(1,1) |
ψ(Ω×2)+ψ(Ω×2)) |
| ωε1+1 |
φ(φ(1,1)+1) |
ψ(Ω×2+1) |
| ωε1+ε0 |
φ(φ(1,1)+φ(1,0)) |
ψ(Ω×2+ψ(Ω)) |
| ωε1×2 |
φ(φ(1,1)+φ(1,1)) |
ψ(Ω×2+ψ(Ω×2)) |
| ωωε1+1 |
φ(φ(φ(1,1)+1)) |
ψ(Ω×2+ψ(Ω×2+1)) |
| ωωε1+ω |
φ(φ(φ(1,1)+φ(1))) |
ψ(Ω×2+ψ(Ω×2+ψ(1))) |
| ωωε1+ε0 |
φ(φ(φ(1,1)+φ(1,0))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω))) |
| ωωε1×2 |
φ(φ(φ(1,1)+φ(1,1))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2))) |
| ωωε1×3 |
φ(φ(φ(1,1)+φ(1,1)+φ(1,1))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2)+ψ(Ω×2))) |
| ωωωε1+1 |
φ(φ(φ(φ(1,1)+1))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+1))) |
| ωωωε1+1+ε1 |
φ(φ(φ(φ(1,1)+1)+φ(1,1))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+1)+ψ(Ω×2))) |
| ωωωε1+1×2 |
φ(φ(φ(φ(1,1)+1)+φ(φ(1,1)+1))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+1)+ψ(Ω×2+1))) |
| ωωωε1+2 |
φ(φ(φ(φ(1,1)+2))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+2))) |
| ωωωε1+ω |
φ(φ(φ(φ(1,1)+φ(1)))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(1)))) |
| ωωωε1+ε0 |
φ(φ(φ(φ(1,1)+φ(1,0)))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω)))) |
| ωωωε1+ωε0+1 |
φ(φ(φ(φ(1,1)+φ(φ(1,0)+1)))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω+1)))) |
| ωωωε1×2 |
φ(φ(φ(φ(1,1)+φ(1,1)))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2)))) |
| ωωωωε1+1 |
φ(φ(φ(φ(φ(1,1)+1)))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+1)))) |
| ωωωωε1+1+1 |
φ(φ(φ(φ(φ(1,1)+1)+1))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+1)+1))) |
| ωωωωε1+1+ε1 |
φ(φ(φ(φ(φ(1,1)+1)+φ(1,1)))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+1)+ψ(Ω×2)))) |
| ωωωωε1+1×2 |
φ(φ(φ(φ(φ(1,1)+1)+φ(φ(1,1)+1)))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+1)+ψ(Ω×2+1)))) |
| ωωωωε1+2 |
φ(φ(φ(φ(φ(1,1)+2)))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+2)))) |
| ωωωωε1+ω |
φ(φ(φ(φ(φ(1,1)+φ(1))))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(1))))) |
| ωωωωε1×2 |
φ(φ(φ(φ(φ(1,1)+φ(1,1))))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2))))) |
| ωωωωωε1+1 |
φ(φ(φ(φ(φ(φ(1,1)+1))))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+1))))) |
| ωωωωωε1×2 |
φ(φ(φ(φ(φ(φ(1,1)+φ(1,1)))))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2)))))) |
| ωωωωωωε1+1 |
φ(φ(φ(φ(φ(φ(φ(1,1)+1)))))) |
ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+1)))))) |
| ε2 |
φ(1,2) = φ(φ(φ(φ(...φ(1,1)+1...)))) |
ψ(Ω×3) = ψ(Ω×2+Ω) = ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+ψ(...)))) |
| ωε2+1 |
φ(φ(1,2)+1) |
ψ(Ω×3+1) |
| ωε2×2 |
φ(φ(1,2)+φ(1,2)) |
ψ(Ω×3+ψ(Ω×3)) |
| ωωε2+1 |
φ(φ(φ(1,2)+1)) |
ψ(Ω×3+ψ(Ω×3+1)) |
| ωωε2×2 |
φ(φ(φ(1,2)+φ(1,2))) |
ψ(Ω×3+ψ(Ω×3+ψ(Ω×3))) |
| ωωωε2+1 |
φ(φ(φ(φ(1,2)+1))) |
ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+1))) |
| ωωωε2×2 |
φ(φ(φ(φ(1,2)+φ(1,2)))) |
ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+ψ(Ω×3)))) |
| ωωωωε2+1 |
φ(φ(φ(φ(φ(1,2)+1)))) |
ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+1)))) |
| ωωωωε2×2 |
φ(φ(φ(φ(φ(1,2)+φ(1,2))))) |
ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+ψ(Ω×3))))) |
| ωωωωωε2+1 |
φ(φ(φ(φ(φ(φ(1,2)+1))))) |
ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+1))))) |
| ωωωωωε2×2 |
φ(φ(φ(φ(φ(φ(1,2)+φ(1,2)))))) |
ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+ψ(Ω×3)))))) |
| ωωωωωωε2+1 |
φ(φ(φ(φ(φ(φ(φ(1,2)+1)))))) |
ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+1)))))) |
| ε3 |
φ(1,3) = φ(φ(φ(φ(...φ(1,2)+1...)))) |
ψ(Ω×4) = ψ(Ω×3+Ω) = ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+ψ(...)))) |
| ε4 |
φ(1,4) = φ(φ(φ(φ(...φ(1,3)+1...)))) |
ψ(Ω×5) = ψ(Ω×4+Ω) = ψ(Ω×4+ψ(Ω×4+ψ(Ω×4+ψ(...)))) |
| εω |
φ(1,ω) = φ(1,φ(1)) |
ψ(Ω×ω) = ψ(Ω×ψ(1)) |
| εω+1 |
φ(1,φ(1))+1 |
ψ(Ω×ω)+1 |
| εω+ω |
φ(1,φ(1))+φ(1) |
ψ(Ω×ω)+ψ(1) |
| εω+ωω |
φ(1,φ(1))+φ(φ(1)) |
ψ(Ω×ω)+ψ(ψ(1)) |
| εω+ε0 |
φ(1,φ(1))+φ(1,0) |
ψ(Ω×ω)+ψ(Ω) |
| εω+ε1 |
φ(1,φ(1))+φ(1,1) |
ψ(Ω×ω)+ψ(Ω×2) |
| εω×2 |
φ(1,φ(1))+φ(1,φ(1)) |
ψ(Ω×ω)+ψ(Ω×ω) |
| εω×2+1 |
φ(1,φ(1))+φ(1,φ(1))+1 |
ψ(Ω×ω)+ψ(Ω×ω)+1 |
| εω×2+ε0 |
φ(1,φ(1))+φ(1,φ(1))+φ(1,0) |
ψ(Ω×ω)+ψ(Ω×ω)+ψ(Ω) |
| εω×3 |
φ(1,φ(1))+φ(1,φ(1))+φ(1,φ(1)) |
ψ(Ω×ω)+ψ(Ω×ω)+ψ(Ω×ω) |
| ωεω+1 |
φ(φ(1,φ(1))+1) |
ψ(Ω×ω+1) |
| ωεω+ω |
φ(φ(1,φ(1))+φ(1)) |
ψ(Ω×ω+ψ(1)) |
| ωεω+ωω |
φ(φ(1,φ(1))+φ(φ(1))) |
ψ(Ω×ω+ψ(ψ(1))) |
| ωεω+ε0 |
φ(φ(1,φ(1))+φ(1,0)) |
ψ(Ω×ω+ψ(Ω)) |
| ωεω×2 |
φ(φ(1,φ(1))+φ(1,φ(1))) |
ψ(Ω×ω+ψ(Ω×ω)) |
| ωωεω+1 |
φ(φ(φ(1,φ(1))+1)) |
ψ(Ω×ω+ψ(Ω×ω+1)) |
| ωωεω+ω |
φ(φ(φ(1,φ(1))+φ(1))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(1))) |
| ωωεω+ε0 |
φ(φ(φ(1,φ(1))+φ(1,0))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω))) |
| ωωεω+ε1 |
φ(φ(φ(1,φ(1))+φ(1,1))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×2))) |
| ωωεω×2 |
φ(φ(φ(1,φ(1))+φ(1,φ(1)))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω))) |
| ωωεω×2+1 |
φ(φ(φ(1,φ(1))+φ(1,φ(1))+1)) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω)+1)) |
| ωωεω×2+ε0 |
φ(φ(φ(1,φ(1))+φ(1,φ(1))+φ(1,0))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω)+ψ(Ω))) |
| ωωεω×3 |
φ(φ(φ(1,φ(1))+φ(1,φ(1))+φ(1,φ(1)))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω)+ψ(Ω×ω))) |
| ωωωεω+1 |
φ(φ(φ(φ(1,φ(1))+1))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+1))) |
| ωωωεω+ω |
φ(φ(φ(φ(1,φ(1))+φ(1)))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(1)))) |
| ωωωεω+ωω |
φ(φ(φ(φ(1,φ(1))+φ(φ(1))))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(ψ(1))))) |
| ωωωεω+ε0 |
φ(φ(φ(φ(1,φ(1))+φ(1,0)))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω)))) |
| ωωωεω×2 |
φ(φ(φ(φ(1,φ(1))+φ(1,φ(1))))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω)))) |
| ωωωωεω+1 |
φ(φ(φ(φ(φ(1,φ(1))+1)))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+1)))) |
| ωωωωεω+ω |
φ(φ(φ(φ(φ(1,φ(1))+φ(1))))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(1))))) |
| ωωωωεω×2 |
φ(φ(φ(φ(φ(1,φ(1))+φ(1,φ(1)))))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω))))) |
| ωωωωωεω+1 |
φ(φ(φ(φ(φ(φ(1,φ(1))+1))))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+1))))) |
| ωωωωωεω+ω |
φ(φ(φ(φ(φ(φ(1,φ(1))+φ(1)))))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(1)))))) |
| ωωωωωεω×2 |
φ(φ(φ(φ(φ(φ(1,φ(1))+φ(1,φ(1))))))) |
ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω+ψ(Ω×ω)))))) |
| εω+1 |
φ(1,φ(1)+1) = φ(φ(φ(φ(...φ(1,φ(1))+1...)))) |
ψ(Ω×ω+Ω) = ψ(Ω×(ω+1)) |
| εω+2 |
φ(1,φ(1)+2) = φ(φ(φ(φ(...φ(1,φ(1)+1)+1...)))) |
ψ(Ω×ω+Ω+Ω) = ψ(Ω×(ω+2)) |
| εω×2 |
φ(1,φ(1)+φ(1)) |
ψ(Ω×ω+Ω×ω) = ψ(Ω×ω×2) |
| εω2 |
φ(1,φ(2)) |
ψ(Ω×ω×ω) = ψ(Ω×ω2) = ψ(Ω×ψ(2)) |
| εωω |
φ(1,φ(φ(1))) |
ψ(Ω×ωω) = ψ(Ω×ψ(ψ(1))) |
| εωωω |
φ(1,φ(φ(φ(1)))) |
ψ(Ω×ωωω) = ψ(Ω×ψ(ψ(ψ(1)))) |
| εωωωω |
φ(1,φ(φ(φ(φ(1))))) |
ψ(Ω×ωωωω) = ψ(Ω×ψ(ψ(ψ(ψ(1))))) |
| εε0 |
φ(1,ε0) = φ(1,φ(1,0)) |
ψ(Ω×ψ(Ω)) = ψ(Ω×ωωω...) = ψ(Ω×ψ(ψ(ψ(ψ(...))))) |
| εε0+1 |
φ(1,φ(1,0))+1 |
ψ(Ω×ψ(Ω))+1 |
| εε0×2 |
φ(1,φ(1,0))+φ(1,φ(1,0)) |
ψ(Ω×ψ(Ω))+ψ(Ω×ψ(Ω)) |
| ωεε0+1 |
φ(φ(1,φ(1,0))+1) |
ψ(Ω×ψ(Ω)+1) |
| ωεε0×2 |
φ(φ(1,φ(1,0))+φ(1,φ(1,0))) |
ψ(Ω×ψ(Ω)+ψ(Ω×ψ(Ω))) |
| ωωεε0+1 |
φ(φ(φ(1,φ(1,0))+1)) |
ψ(Ω×ψ(Ω)+ψ(Ω×ψ(Ω)+1)) |
| ωωεε0×2 |
φ(φ(φ(1,φ(1,0))+φ(1,φ(1,0)))) |
ψ(Ω×ψ(Ω)+ψ(Ω×ψ(Ω)+ψ(Ω×ψ(Ω)))) |
| εε0+1 |
φ(1,φ(1,0)+1) |
ψ(Ω×ψ(Ω)+Ω) = ψ(Ω×ψ(Ω)+ψ(Ω×ψ(Ω)+...)) |
| εε0+ω |
φ(1,φ(1,0)+φ(1)) |
ψ(Ω×ψ(Ω)+Ω×ψ(1)) |
| εε0+ωω |
φ(1,φ(1,0)+φ(φ(1))) |
ψ(Ω×ψ(Ω)+Ω×ψ(ψ(1))) |
| εε0+ωωω |
φ(1,φ(1,0)+φ(φ(φ(1)))) |
ψ(Ω×ψ(Ω)+Ω×ψ(ψ(ψ(1)))) |
| εε0×2 |
φ(1,φ(1,0)+φ(1,0)) |
ψ(Ω×ψ(Ω)+Ω×ψ(Ω)) |
| εε0×2+1 |
φ(1,φ(1,0)+φ(1,0)+1) |
ψ(Ω×ψ(Ω)+Ω×ψ(Ω)+Ω) |
| εε0×3 |
φ(1,φ(1,0)+φ(1,0)+φ(1,0)) |
ψ(Ω×ψ(Ω)+Ω×ψ(Ω)+Ω×ψ(Ω)) |
| εωε0+1 |
φ(1,φ(φ(1,0)+1)) |
ψ(Ω×ψ(Ω+1)) = ψ(Ω×ψ(Ω)+Ω×ψ(Ω)+Ω×ψ(Ω)+...) |
| εε0×ω+εε0 |
φ(1,φ(φ(1,0)+1))+φ(1,φ(1,0)+1) |
ψ(Ω×ψ(Ω+1))+ψ(Ω×ψ(Ω)) |
| εε0×ω×2 |
φ(1,φ(φ(1,0)+1))+φ(1,φ(φ(1,0)+1)) |
ψ(Ω×ψ(Ω+1))+ψ(Ω×ψ(Ω+1)) |
| ωεε0×ω+1 |
φ(φ(1,φ(φ(1,0)+1))+1) |
ψ(Ω×ψ(Ω+1)+1) |
| εωε0+1+1 |
φ(1,φ(φ(1,0)+1)+1) |
ψ(Ω×ψ(Ω+1)+Ω) |
| εωε0+1×2 |
φ(1,φ(φ(1,0)+1)+φ(φ(1,0)+1)) |
ψ(Ω×ψ(Ω+1)+Ω×ψ(Ω+1)) |
| εωε0+2 |
φ(1,φ(φ(1,0)+2)) |
ψ(Ω×ψ(Ω+2)) |
| εωε0+ω |
φ(1,φ(φ(1,0)+φ(1))) |
ψ(Ω×ψ(Ω+ψ(1))) |
| εωε0×2 |
φ(1,φ(φ(1,0)+φ(1,0))) |
ψ(Ω×ψ(Ω+ψ(Ω))) |
| εωωε0+1 |
φ(1,φ(φ(φ(1,0)+1))) |
ψ(Ω×ψ(Ω+ψ(Ω+1))) |
| εωωε0+2 |
φ(1,φ(φ(φ(1,0)+2))) |
ψ(Ω×ψ(Ω+ψ(Ω+2))) |
| εωωε0+ω |
φ(1,φ(φ(φ(1,0)+φ(1)))) |
ψ(Ω×ψ(Ω+ψ(Ω+ψ(1)))) |
| εωωε0×2 |
φ(1,φ(φ(φ(1,0)+φ(1,0)))) |
ψ(Ω×ψ(Ω+ψ(Ω+ψ(Ω)))) |
| εωωωε0+1 |
φ(1,φ(φ(φ(φ(1,0)+1)))) |
ψ(Ω×ψ(Ω+ψ(Ω+ψ(Ω+1)))) |
| εωωωε0+ω |
φ(1,φ(φ(φ(φ(1,0)+φ(1))))) |
ψ(Ω×ψ(Ω+ψ(Ω+ψ(Ω+ψ(1))))) |
| εωωωε0×2 |
φ(1,φ(φ(φ(φ(1,0)+φ(1,0))))) |
ψ(Ω×ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω))))) |
| εωωωωε0+1 |
φ(1,φ(φ(φ(φ(1,0)+1)))) |
ψ(Ω×ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+1))))) |
| εωωωωε0+ω |
φ(1,φ(φ(φ(φ(1,0)+φ(1))))) |
ψ(Ω×ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(1)))))) |
| εωωωωε0×2 |
φ(1,φ(φ(φ(φ(1,0)+φ(1,0))))) |
ψ(Ω×ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω+ψ(Ω)))))) |
| εε1 |
φ(1,ε1) = φ(1,φ(1,1)) = φ(1,φ(φ(φ(...φ(1,0)+1...)))) |
ψ(Ω×ψ(Ω×2)) = ψ(Ω×ψ(Ω+ψ(Ω+ψ(Ω+...)))) |
| εε1+1 |
φ(1,φ(1,1))+1 |
ψ(Ω×ψ(Ω×2))+1 |
| εε1×2 |
φ(1,φ(1,1))+φ(1,φ(1,1)) |
ψ(Ω×ψ(Ω×2))+ψ(Ω×ψ(Ω×2)) |
| ωεε1+1 |
φ(φ(1,φ(1,1))+1) |
ψ(Ω×ψ(Ω×2)+1) |
| ωεε1×2 |
φ(φ(1,φ(1,1))+φ(1,φ(1,1))) |
ψ(Ω×ψ(Ω×2)+ψ(Ω×ψ(Ω×2))) |
| ωωεε1+1 |
φ(φ(φ(1,φ(1,1))+1)) |
ψ(Ω×ψ(Ω×2)+ψ(Ω×ψ(Ω×2)+1)) |
| εε1+1 |
φ(1,φ(1,1)+1) |
ψ(Ω×ψ(Ω×2)+Ω) |
| εε1+ε0 |
φ(1,φ(1,1)+φ(1,0)) |
ψ(Ω×ψ(Ω×2)+Ω×ψ(Ω)) |
| εε1×2 |
φ(1,φ(1,1)+φ(1,1)) |
ψ(Ω×ψ(Ω×2)+Ω×ψ(Ω×2)) |
| εωε1+1 |
φ(1,φ(φ(1,1)+1)) |
ψ(Ω×ψ(Ω×2+1)) = ψ(Ω×ψ(Ω×2)+Ω×ψ(Ω×2)+...) |
| εωε1+ω |
φ(1,φ(φ(1,1)+φ(1))) |
ψ(Ω×ψ(Ω×2+ψ(1))) |
| εωε1×2 |
φ(1,φ(φ(1,1)+φ(1,1))) |
ψ(Ω×ψ(Ω×2+ψ(Ω×2))) |
| εωωε1+1 |
φ(1,φ(φ(φ(1,1)+1))) |
ψ(Ω×ψ(Ω×2+ψ(Ω×2+1))) |
| εωωε1+ω |
φ(1,φ(φ(φ(1,1)+φ(1)))) |
ψ(Ω×ψ(Ω×2+ψ(Ω×2+ψ(1)))) |
| εωωε1×2 |
φ(1,φ(φ(φ(1,1)+φ(1,1)))) |
ψ(Ω×ψ(Ω×2+ψ(Ω×2+ψ(Ω×2)))) |
| εε2 |
φ(1,φ(1,2)) = φ(1,φ(φ(φ(φ(...φ(1,1)+1...))))) |
ψ(Ω×ψ(Ω×3)) = ψ(Ω×ψ(Ω×2+ψ(Ω×2+ψ(Ω×2+...)))) |
| εε3 |
φ(1,φ(1,3)) = φ(1,φ(φ(φ(φ(...φ(1,2)+1...))))) |
ψ(Ω×ψ(Ω×4)) = ψ(Ω×ψ(Ω×3+ψ(Ω×3+ψ(Ω×3+...)))) |
| εεω |
φ(1,εω) = φ(1,φ(1,φ(1))) |
ψ(Ω×ψ(Ω×ω)) = ψ(Ω×ψ(Ω×ψ(1))) |
| εεω+1 |
φ(1,φ(1,φ(1))+1) |
ψ(Ω×ψ(Ω×ω)+Ω) |
| εεω×2 |
φ(1,φ(1,φ(1))+φ(1,φ(1))) |
ψ(Ω×ψ(Ω×ω)+Ω×ψ(Ω×ω)) |
| εεω×ω |
φ(1,φ(φ(1,φ(1))+1)) |
ψ(Ω×ψ(Ω×ω+1) |
| εεω+1 |
φ(1,φ(1,φ(1)+1)) |
ψ(Ω×ψ(Ω×ω+Ω)) |
| εεω+2 |
φ(1,φ(1,φ(1)+2)) |
ψ(Ω×ψ(Ω×ω+Ω+Ω)) |
| εεω×2 |
φ(1,φ(1,φ(1)+φ(1))) |
ψ(Ω×ψ(Ω×ω×2)) |
| εεω2 |
φ(1,φ(1,φ(2))) |
ψ(Ω×ψ(Ω×ω2)) = ψ(Ω×ψ(Ω×ψ(2))) |
| εεωω |
φ(1,φ(1,φ(φ(1)))) |
ψ(Ω×ψ(Ω×ωω)) = ψ(Ω×ψ(Ω×ψ(ψ(1)))) |
| εεε0 |
φ(1,εε0) = φ(1,φ(1,φ(1,0))) |
ψ(Ω×ψ(Ω×ψ(Ω))) |
| εεε0+1 |
φ(1,φ(1,φ(1,0))+1) |
ψ(Ω×ψ(Ω×ψ(Ω))+Ω) |
| εεε0+ε0 |
φ(1,φ(1,φ(1,0))+φ(1,0)) |
ψ(Ω×ψ(Ω×ψ(Ω))+Ω×ψ(Ω)) |
| εεε0×2 |
φ(1,φ(1,φ(1,0))+φ(1,φ(1,0))) |
ψ(Ω×ψ(Ω×ψ(Ω))+Ω×ψ(Ω×ψ(Ω))) |
| ε(εε0)ω |
φ(1,φ(φ(1,φ(1,0))+1)) |
ψ(Ω×ψ(Ω×ψ(Ω)+1)) |
| εεε0+1 |
φ(1,φ(1,φ(1,0)+1)) |
ψ(Ω×ψ(Ω×ψ(Ω)+Ω)) |
| εεε0×2 |
φ(1,φ(1,φ(1,0)+φ(1,0))) |
ψ(Ω×ψ(Ω×ψ(Ω)+Ω×ψ(Ω))) |
| εεε0×ω |
φ(1,φ(1,φ(φ(1,0)+1))) |
ψ(Ω×ψ(Ω×ψ(Ω+1))) |
| εεε1 |
φ(1,φ(1,φ(1,1))) |
ψ(Ω×ψ(Ω×ψ(Ω×2))) |
| εεεω |
φ(1,φ(1,φ(1,φ(1)))) |
ψ(Ω×ψ(Ω×ψ(Ω×ψ(1)))) |
| εεεε0 |
φ(1,εεε0) = φ(1,φ(1,φ(1,φ(1,0)))) |
ψ(Ω×ψ(Ω×ψ(Ω×ψ(Ω)))) |
| εεεεω |
φ(1,φ(1,φ(1,φ(1,φ(1))))) |
ψ(Ω×ψ(Ω×ψ(Ω×ψ(Ω×ψ(1))))) |
| εεεεε0 |
φ(1,εεεε0) = φ(1,φ(1,φ(1,φ(1,φ(1,0))))) |
ψ(Ω×ψ(Ω×ψ(Ω×ψ(Ω×ψ(Ω))))) |
| ζ0 |
φ(2,0) = φ(1,φ(1,φ(1,φ(1,...))) |
ψ(Ω2) = ψ(Ω×Ω) = ψ(Ω×ψ(Ω×ψ(Ω×ψ(...)))) |
| ζ0+1 |
φ(2,0)+1 |
ψ(Ω2)+1 |
| ζ0+ω |
φ(2,0)+φ(1) |
ψ(Ω2)+ψ(1) |
| ζ0+ε0 |
φ(2,0)+φ(1,0) |
ψ(Ω2)+ψ(Ω) |
| ζ0×2 |
φ(2,0)+φ(2,0) |
ψ(Ω2)+ψ(Ω2) |
| ωζ0+1 |
φ(φ(2,0)+1) |
ψ(Ω2+1) |
| ωζ0+ω |
φ(φ(2,0)+φ(1)) |
ψ(Ω2+ψ(1)) |
| ωζ0+ε0 |
φ(φ(2,0)+φ(1,0)) |
ψ(Ω2+ψ(Ω)) |
| ωζ0×2 |
φ(φ(2,0)+φ(2,0)) |
ψ(Ω2+ψ(Ω2)) |
| ωωζ0+1 |
φ(φ(φ(2,0)+1)) |
ψ(Ω2+ψ(Ω2+1)) |
| ωωζ0+ω |
φ(φ(φ(2,0)+φ(1))) |
ψ(Ω2+ψ(Ω2+ψ(1))) |
| ωωζ0+ε0 |
φ(φ(φ(2,0)+φ(1,0))) |
ψ(Ω2+ψ(Ω2+ψ(Ω))) |
| ωωζ0×2 |
φ(φ(φ(2,0)+φ(2,0))) |
ψ(Ω2+ψ(Ω2+ψ(Ω2))) |
| ωωωζ0+1 |
φ(φ(φ(φ(2,0)+1))) |
ψ(Ω2+ψ(Ω2+ψ(Ω2+1))) |
| ωωωζ0×2 |
φ(φ(φ(φ(2,0)+φ(2,0)))) |
ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2)))) |
| ωωωωζ0+1 |
φ(φ(φ(φ(φ(2,0)+1)))) |
ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+1)))) |
| ωωωωζ0×2 |
φ(φ(φ(φ(φ(2,0)+φ(2,0))))) |
ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2))))) |
| ωωωωωζ0+1 |
φ(φ(φ(φ(φ(φ(2,0)+1))))) |
ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+1))))) |
| ωωωωωζ0×2 |
φ(φ(φ(φ(φ(φ(2,0)+φ(2,0)))))) |
ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2)))))) |
| ωωωωωωζ0+1 |
φ(φ(φ(φ(φ(φ(φ(2,0)+1)))))) |
ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+1)))))) |
| εζ0+1 |
φ(1,φ(2,0)+1) = φ(φ(φ(φ(φ(φ(...φ(2,0)+1...)))))) |
ψ(Ω2+Ω) = ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+...)))) |
| εζ0+1+1 |
φ(1,φ(2,0)+1)+1 |
ψ(Ω2+Ω)+1 |
| εζ0+1+ζ0 |
φ(1,φ(2,0)+1)+φ(2,0) |
ψ(Ω2+Ω)+ψ(Ω2) |
| εζ0+1×2 |
φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1) |
ψ(Ω2+Ω)+ψ(Ω2+Ω) |
| εζ0+1×2+1 |
φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)+1 |
ψ(Ω2+Ω)+ψ(Ω2+Ω)+1 |
| εζ0+1×2+ζ0 |
φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)+φ(2,0) |
ψ(Ω2+Ω)+ψ(Ω2+Ω)+ψ(Ω2) |
| ζ0+1×3 |
φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1) |
ψ(Ω2+Ω)+ψ(Ω2+Ω)+ψ(Ω2+Ω) |
| ωεζ0+1+1 |
φ(φ(1,φ(2,0)+1)+1) |
ψ(Ω2+Ω+1) |
| ωεζ0+1+ζ0 |
φ(φ(1,φ(2,0)+1)+φ(2,0)) |
ψ(Ω2+Ω+ψ(Ω2)) |
| ωεζ0+1×2 |
φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)) |
ψ(Ω2+Ω+ψ(Ω2+Ω)) |
| ωωεζ0+1+1 |
φ(φ(φ(1,φ(2,0)+1)+1)) |
ψ(Ω2+Ω+ψ(Ω2+Ω+1)) |
| ωωεζ0+1+ζ0 |
φ(φ(φ(1,φ(2,0)+1)+φ(2,0))) |
ψ(Ω2+Ω+ψ(Ω2+Ω+ψ(Ω2))) |
| ωωεζ0+1×2 |
φ(φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1))) |
ψ(Ω2+Ω+ψ(Ω2+Ω+ψ(Ω2+Ω))) |
| ωωεζ0+1×2+1 |
φ(φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)+1)) |
ψ(Ω2+Ω+ψ(Ω2+Ω+ψ(Ω2+Ω)+1)) |
| ωωεζ0+1×2+ζ0 |
φ(φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)+φ(2,0))) |
ψ(Ω2+Ω+ψ(Ω2+Ω+ψ(Ω2+Ω)+ψ(Ω2))) |
| ωωεζ0+1×3 |
φ(φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1))) |
ψ(Ω2+Ω+ψ(Ω2+Ω+ψ(Ω2+Ω)+ψ(Ω2+Ω))) |
| ωωωεζ0+1+1 |
φ(φ(φ(φ(1,φ(2,0)+1)+1))) |
ψ(Ω2+Ω+ψ(Ω2+Ω+ψ(Ω2+Ω+1))) |
| ωωωεζ0+1×2 |
φ(φ(φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)))) |
ψ(Ω2+Ω+ψ(Ω2+Ω+ψ(Ω2+Ω+ψ(Ω2+Ω)))) |
| ωωωωεζ0+1+1 |
φ(φ(φ(φ(φ(1,φ(2,0)+1)+1)))) |
ψ(Ω2+Ω+ψ(Ω2+Ω+ψ(Ω2+Ω+ψ(Ω2+Ω+1)))) |
| εζ0+2 |
φ(1,φ(2,0)+2) = φ(φ(φ(φ(...φ(1,φ(2,0)+1)+1...)))) |
ψ(Ω2+Ω+Ω) |
| εζ0+ω |
φ(1,φ(2,0)+φ(1)) |
ψ(Ω2+Ω×ω) = ψ(Ω2+Ω×ψ(1)) |
| εζ0+ωω |
φ(1,φ(2,0)+φ(φ(1))) |
ψ(Ω2+Ω×ψ(ψ(1))) |
| εζ0+ε0 |
φ(1,φ(2,0)+φ(1,0)) |
ψ(Ω2+Ω×ψ(Ω)) |
| εζ0+ε1 |
φ(1,φ(2,0)+φ(1,1)) |
ψ(Ω2+Ω×ψ(Ω×2)) |
| εζ0+εε0 |
φ(1,φ(2,0)+φ(1,φ(1,0))) |
ψ(Ω2+Ω×ψ(Ω×ψ(Ω))) |
| εζ0×2 |
φ(1,φ(2,0)+φ(2,0)) |
ψ(Ω2+Ω×ψ(Ω2)) |
| εζ0×2+1 |
φ(1,φ(2,0)+φ(2,0)+1) |
ψ(Ω2+Ω×ψ(Ω2)+Ω) |
| εζ0×3 |
φ(1,φ(2,0)+φ(2,0)+φ(2,0)) |
ψ(Ω2+Ω×ψ(Ω2)+Ω×ψ(Ω2)) |
| εωζ0+1 |
φ(1,φ(φ(2,0)+1)) |
ψ(Ω2+Ω×ψ(Ω2+1)) |
| εωζ0×2 |
φ(1,φ(φ(2,0)+φ(2,0))) |
ψ(Ω2+Ω×ψ(Ω2+ψ(Ω2))) |
| εωωζ0+1 |
φ(1,φ(φ(φ(2,0)+1))) |
ψ(Ω2+Ω×ψ(Ω2+ψ(Ω2+1))) |
| εωωζ0×2 |
φ(1,φ(φ(φ(2,0)+φ(2,0)))) |
ψ(Ω2+Ω×ψ(Ω2+ψ(Ω2+ψ(Ω2)))) |
| εωωωζ0+1 |
φ(1,φ(φ(φ(φ(2,0)+1)))) |
ψ(Ω2+Ω×ψ(Ω2+ψ(Ω2+ψ(Ω2+1)))) |
| εωωωζ0×2 |
φ(1,φ(φ(φ(φ(2,0)+φ(2,0))))) |
ψ(Ω2+Ω×ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2))))) |
| εωωωωζ0+1 |
φ(1,φ(φ(φ(φ(φ(2,0)+1))))) |
ψ(Ω2+Ω×ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+1))))) |
| εωωωωζ0×2 |
φ(1,φ(φ(φ(φ(φ(2,0)+φ(2,0)))))) |
ψ(Ω2+Ω×ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2+ψ(Ω2)))))) |
| εεζ0+1 |
φ(1,φ(1,φ(2,0)+1)) |
ψ(Ω2+Ω×ψ(Ω2+Ω)) |
| εεζ0+1+1 |
φ(1,φ(1,φ(2,0)+1)+1) |
ψ(Ω2+Ω×ψ(Ω2+Ω)+Ω) |
| εεζ0+1×2 |
φ(1,φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1)) |
ψ(Ω2+Ω×ψ(Ω2+Ω)+Ω×ψ(Ω2+Ω)) |
| εωεζ0+1+1 |
φ(1,φ(φ(1,φ(2,0)+1)+1)) |
ψ(Ω2+Ω×ψ(Ω2+Ω+1)) |
| εωεζ0+1×2 |
φ(1,φ(φ(1,φ(2,0)+1)+φ(1,φ(2,0)+1))) |
ψ(Ω2+Ω×ψ(Ω2+Ω+ψ(Ω2+Ω))) |
| εωωεζ0+1+1 |
φ(1,φ(φ(φ(1,φ(2,0)+1)+1))) |
ψ(Ω2+Ω×ψ(Ω2+Ω+ψ(Ω2+Ω+1))) |
| εεζ0+2 |
φ(1,φ(1,φ(2,0)+2)) |
ψ(Ω2+Ω×ψ(Ω2+Ω×2)) |
| εεζ0+ω |
φ(1,φ(1,φ(2,0)+φ(1))) |
ψ(Ω2+Ω×ψ(Ω2+Ω×ω)) |
| εεζ0+ε0 |
φ(1,φ(1,φ(2,0)+φ(1,0))) |
ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω))) |
| εεζ0×2 |
φ(1,φ(1,φ(2,0)+φ(2,0))) |
ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2))) |
| εεζ0×3 |
φ(1,φ(1,φ(2,0)+φ(2,0)+φ(2,0))) |
ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2)+Ω×ψ(Ω2))) |
| εεωζ0+1 |
φ(1,φ(1,φ(φ(2,0)+1))) |
ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2+1))) |
| εεωζ0×2 |
φ(1,φ(1,φ(φ(2,0)+φ(2,0)))) |
ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2+ψ(Ω2)))) |
| εεωωζ0+1 |
φ(1,φ(1,φ(φ(φ(2,0)+1)))) |
ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2+ψ(Ω2+1)))) |
| εεωωζ0×2 |
φ(1,φ(1,φ(φ(φ(2,0)+φ(2,0))))) |
ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2+ψ(Ω2+ψ(Ω2))))) |
| εεεζ0+1 |
φ(1,φ(1,φ(1,φ(2,0)+1))) |
ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2+Ω))) |
| εεεζ0+2 |
φ(1,φ(1,φ(1,φ(2,0)+2))) |
ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2+Ω×2))) |
| εεεζ0+ω |
φ(1,φ(1,φ(1,φ(2,0)+φ(1)))) |
ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2+Ω×ω))) |
| εεεζ0×2 |
φ(1,φ(1,φ(1,φ(2,0)+φ(2,0)))) |
ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2)))) |
| ζ1 |
φ(2,1) = φ(1,φ(1,φ(1,φ(1,...φ(2,0)+1...)))) |
ψ(Ω2×2) = ψ(Ω2+Ω×Ω) =
ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2+Ω×...))) |
| εζ1+1 |
φ(1,φ(2,1)+1) = φ(φ(φ(φ(φ(φ(...φ(2,1)+1...)))))) |
ψ(Ω2×2+Ω) = ψ(Ω2×2+ψ(Ω2×2+ψ(Ω2×2+...))) |
| εζ1+ω |
φ(1,φ(2,1)+φ(1)) |
ψ(Ω2×2+Ω×ω) |
| εζ1+ζ0 |
φ(1,φ(2,1)+φ(2,0)) |
ψ(Ω2×2+Ω×ψ(Ω2)) |
| εζ1×2 |
φ(1,φ(2,1)+φ(2,1)) |
ψ(Ω2×2+Ω×ψ(Ω2×2)) |
| εωζ1+1 |
φ(1,φ(φ(2,1)+1)) |
ψ(Ω2×2+Ω×ψ(Ω2×2+1)) |
| εωζ1×2 |
φ(1,φ(φ(2,1)+φ(2,1))) |
ψ(Ω2×2+Ω×ψ(Ω2×2+ψ(Ω2×2))) |
| εωωζ1+1 |
φ(1,φ(φ(φ(2,1)+1))) |
ψ(Ω2×2+Ω×ψ(Ω2×2+ψ(Ω2×2+1))) |
| εωωζ1×2 |
φ(1,φ(φ(φ(2,1)+φ(2,1)))) |
ψ(Ω2×2+Ω×ψ(Ω2×2+ψ(Ω2×2+ψ(Ω2×2)))) |
| εεζ1+1 |
φ(1,φ(1,φ(2,1)+1)) |
ψ(Ω2×2+Ω×ψ(Ω2×2+Ω)) |
| εεζ1+ω |
φ(1,φ(1,φ(2,1)+φ(1))) |
ψ(Ω2×2+Ω×ψ(Ω2×2+Ω×ω)) |
| εεζ1×2 |
φ(1,φ(1,φ(2,1)+φ(2,1))) |
ψ(Ω2×2+Ω×ψ(Ω2×2+Ω×ψ(Ω2×2))) |
| εεεζ1+1 |
φ(1,φ(1,φ(1,φ(2,1)+1))) |
ψ(Ω2×2+Ω×ψ(Ω2×2+Ω×ψ(Ω2×2+Ω))) |
| εεεζ1×2 |
φ(1,φ(1,φ(1,φ(2,1)+(2,1)))) |
ψ(Ω2×2+Ω×ψ(Ω2×2+Ω×ψ(Ω2×2+Ω×ψ(Ω2×2)))) |
| ζ2 |
φ(2,2) |
ψ(Ω2×3) = ψ(Ω2×2+Ω×Ω) |
| ζ3 |
φ(2,3) |
ψ(Ω2×4) |
| ζω |
φ(2,ω) = φ(2,φ(1)) |
ψ(Ω2×ω) = ψ(Ω2×ψ(1)) |
| ζωω |
φ(2,φ(φ(1))) |
ψ(Ω2×ψ(ψ(1))) |
| ζε0 |
φ(2,φ(1,0)) |
ψ(Ω2×ψ(Ω)) |
| ζζ0 |
φ(2,φ(2,0)) |
ψ(Ω2×ψ(Ω2)) |
| εζζ0+1 |
φ(1,φ(2,φ(2,0))+1) |
ψ(Ω2×ψ(Ω2)+Ω) |
| ζζ0+1 |
φ(2,φ(2,0)+1) |
ψ(Ω2×ψ(Ω2)+Ω2) |
| ζζ0×2 |
φ(2,φ(2,0)+φ(2,0)) |
ψ(Ω2×ψ(Ω2)+Ω2×ψ(Ω2)) |
| ζωζ0+1 |
φ(2,φ(φ(2,0)+1)) |
ψ(Ω2×ψ(Ω2+1)) = ψ(Ω2×ψ(Ω2)+Ω2×ψ(Ω2)+...) |
| ζωζ0×2 |
φ(2,φ(φ(2,0)+φ(2,0))) |
ψ(Ω2×ψ(Ω2+ψ(Ω2))) |
| ζωωζ0+1 |
φ(2,φ(φ(φ(2,0)+1))) |
ψ(Ω2×ψ(Ω2+ψ(Ω2+1))) |
| ζωωζ0×2 |
φ(2,φ(φ(φ(2,0)+φ(2,0)))) |
ψ(Ω2×ψ(Ω2+ψ(Ω2+ψ(Ω2)))) |
| ζεζ0+1 |
φ(2,φ(1,φ(2,0)+1)) |
ψ(Ω2×ψ(Ω2+Ω)) |
| ζεζ0+2 |
φ(2,φ(1,φ(2,0)+2)) |
ψ(Ω2×ψ(Ω2+Ω×2)) |
| ζεζ0×2 |
φ(2,φ(1,φ(2,0)+φ(2,0))) |
ψ(Ω2×ψ(Ω2+Ω×ψ(Ω2))) |
| ζεεζ0+1 |
φ(2,φ(1,φ(1,φ(2,0)+1))) |
ψ(Ω2×ψ(Ω2+Ω×ψ(Ω2+Ω))) |
| ζεεζ0×2 |
φ(2,φ(1,φ(1,φ(2,0)+φ(2,0)))) |
ψ(Ω2×ψ(Ω2+Ω×ψ(Ω2+Ω×ψ(Ω2)))) |
| ζζ1 |
φ(2,φ(2,1)) |
ψ(Ω2×ψ(Ω2×2)) |
| ζζ2 |
φ(2,φ(2,2)) |
ψ(Ω2×ψ(Ω2×3)) |
| ζζω |
φ(2,φ(2,φ(1))) |
ψ(Ω2×ψ(Ω2×ω)) |
| ζζε0 |
φ(2,φ(2,φ(1,0))) |
ψ(Ω2×ψ(Ω2×ψ(Ω))) |
| ζζζ0 |
φ(2,φ(2,φ(2,0))) |
ψ(Ω2×ψ(Ω2×ψ(Ω2))) |
| ζζζ0+1 |
φ(2,φ(2,φ(2,0))+1) |
ψ(Ω2×ψ(Ω2×ψ(Ω2))+Ω2) |
| ζζζ0×2 |
φ(2,φ(2,φ(2,0))+φ(2,φ(2,0))) |
ψ(Ω2×ψ(Ω2×ψ(Ω2))+Ω2×ψ(Ω2×ψ(Ω2))) |
| ζζζ0×ω |
φ(2,φ(φ(2,φ(2,0))+1)) |
ψ(Ω2×ψ(Ω2×ψ(Ω2)+1)) |
| ζζζ0+1 |
φ(2,φ(2,φ(2,0)+1)) |
ψ(Ω2×ψ(Ω2×ψ(Ω2)+Ω2)) |
| ζζζ0×2 |
φ(2,φ(2,φ(2,0)+φ(2,0))) |
ψ(Ω2×ψ(Ω2×ψ(Ω2)+Ω2×ψ(Ω2))) |
| ζζζ0×ω |
φ(2,φ(2,φ(φ(2,0)+1))) |
ψ(Ω2×ψ(Ω2×ψ(Ω2+1))) |
| ζζζ1 |
φ(2,φ(2,φ(2,1))) |
ψ(Ω2×ψ(Ω2×ψ(Ω2×2))) |
| ζζζω |
φ(2,φ(2,φ(2,φ(1)))) |
ψ(Ω2×ψ(Ω2×ψ(Ω2×ψ(1)))) |
| ζζζζ0 |
φ(2,φ(2,φ(2,φ(2,0)))) |
ψ(Ω2×ψ(Ω2×ψ(Ω2×ψ(Ω2)))) |
| ζζζζω |
φ(2,φ(2,φ(2,φ(2,φ(1))))) |
ψ(Ω2×ψ(Ω2×ψ(Ω2×ψ(Ω2×ψ(1))))) |
| ζζζζζ0 |
φ(2,φ(2,φ(2,φ(2,φ(2,0))))) |
ψ(Ω2×ψ(Ω2×ψ(Ω2×ψ(Ω2×ψ(Ω2))))) |
| η0 |
φ(3,0) = φ(2,φ(2,φ(2,φ(2,...))) |
ψ(Ω3) = ψ(Ω2×Ω)= ψ(Ω2×ψ(Ω2×ψ(Ω2×ψ(...)))) |
| η0+1 |
φ(3,0)+1 |
ψ(Ω3)+ψ(0) |
| η0+ω |
φ(3,0)+φ(1) |
ψ(Ω3)+ψ(1) |
| η0×2 |
φ(3,0)+φ(3,0) |
ψ(Ω3)+ψ(Ω3) |
| ωη0+1 |
φ(φ(3,0)+1) |
ψ(Ω3+ψ(0)) |
| ωη0×2 |
φ(φ(3,0)+φ(3,0)) |
ψ(Ω3+ψ(Ω3)) |
| ωωη0+1 |
φ(φ(φ(3,0)+1)) |
ψ(Ω3+ψ(Ω3+1)) |
| ωωη0×2 |
φ(φ(φ(3,0)+φ(3,0))) |
ψ(Ω3+ψ(Ω3+ψ(Ω3))) |
| ωωωη0+1 |
φ(φ(φ(φ(3,0)+1))) |
ψ(Ω3+ψ(Ω3+ψ(Ω3+1))) |
| ωωωη0×2 |
φ(φ(φ(φ(3,0)+φ(3,0)))) |
ψ(Ω3+ψ(Ω3+ψ(Ω3+ψ(Ω3)))) |
| ωωωωη0+1 |
φ(φ(φ(φ(φ(3,0)+1)))) |
ψ(Ω3+ψ(Ω3+ψ(Ω3+ψ(Ω3+1)))) |
| ωωωωη0×2 |
φ(φ(φ(φ(φ(3,0)+φ(3,0))))) |
ψ(Ω3+ψ(Ω3+ψ(Ω3+ψ(Ω3+ψ(Ω3))))) |
| ωωωωωη0+1 |
φ(φ(φ(φ(φ(φ(3,0)+1))))) |
ψ(Ω3+ψ(Ω3+ψ(Ω3+ψ(Ω3+ψ(Ω3+1))))) |
| εη0+1 |
φ(1,φ(3,0)+1) = φ(φ(φ(φ(φ(φ(...φ(3,0)+1...)))))) |
ψ(Ω3+Ω) = ψ(Ω3+ψ(Ω3+ψ(Ω3+...))) |
| εη0+2 |
φ(1,φ(3,0)+2) |
ψ(Ω3+Ω+Ω) |
| εη0+ω |
φ(1,φ(3,0)+φ(1)) |
ψ(Ω3+Ω×ω) |
| εη0+ε0 |
φ(1,φ(3,0)+φ(1,0)) |
ψ(Ω3+Ω×ψ(Ω)) |
| εη0+ζ0 |
φ(1,φ(3,0)+φ(2,0)) |
ψ(Ω3+Ω×ψ(Ω2)) |
| εη0×2 |
φ(1,φ(3,0)+φ(3,0)) |
ψ(Ω3+Ω×ψ(Ω3)) |
| εεη0+1 |
φ(1,φ(1,φ(3,0)+1)) |
ψ(Ω3+Ω×ψ(Ω3+Ω)) |
| εεη0×2 |
φ(1,φ(1,φ(3,0)+1)) |
ψ(Ω3+Ω×ψ(Ω3+Ω×ψ(Ω3))) |
| εεεη0+1 |
φ(1,φ(1,φ(3,0)+φ(3,0))) |
ψ(Ω3+Ω×ψ(Ω3+Ω×ψ(Ω3+Ω))) |
| ζη0+1 |
φ(2,φ(3,0)+1) |
ψ(Ω3+Ω2) = ψ(Ω3+Ω×Ω) |
| εζη0+1+1 |
φ(1,φ(2,φ(3,0)+1)+1) |
ψ(Ω3+Ω2+Ω) |
| ζη0+2 |
φ(2,φ(3,0)+2) |
ψ(Ω3+Ω2+Ω2) |
| ζη0+ω |
φ(2,φ(3,0)+φ(1)) |
ψ(Ω3+Ω2×ω) |
| ζη0+ε0 |
φ(2,φ(3,0)+φ(1,0)) |
ψ(Ω3+Ω2×ψ(Ω)) |
| ζη0+ζ0 |
φ(2,φ(3,0)+φ(2,0)) |
ψ(Ω3+Ω2×ψ(Ω2)) |
| ζη0×2 |
φ(2,φ(3,0)+φ(3,0)) |
ψ(Ω3+Ω2×ψ(Ω3)) |
| ζεη0+1 |
φ(2,φ(1,φ(3,0)+1)) |
ψ(Ω3+Ω2×ψ(Ω3+Ω)) |
| ζζη0+1 |
φ(2,φ(2,φ(3,0)+1)) |
ψ(Ω3+Ω2×ψ(Ω3+Ω2)) |
| ζζη0×2 |
φ(2,φ(2,φ(3,0)+φ(3,0))) |
ψ(Ω3+Ω2×ψ(Ω3+Ω2×ψ(Ω3))) |
| ζζζη0+1 |
φ(2,φ(2,φ(2,φ(3,0)+1))) |
ψ(Ω3+Ω2×ψ(Ω3+Ω2×ψ(Ω3+Ω2))) |
| η1 |
φ(3,1) = φ(2,φ(2,φ(2,φ(2,...φ(3,0)+1...)))) |
ψ(Ω3×2) = ψ(Ω3+Ω2×Ω) =
ψ(Ω3+Ω2×ψ(Ω3+Ω2×ψ(Ω3+Ω2×...))) |
| η2 |
φ(3,2) |
ψ(Ω3×3) |
| ηω |
φ(3,ω) |
ψ(Ω3×ψ(1)) |
| ηωω |
φ(3,φ(φ(1))) |
ψ(Ω3×ψ(ψ(1))) |
| ηε0 |
φ(3,φ(1,0)) |
ψ(Ω3×ψ(Ω)) |
| ηζ0 |
φ(3,φ(2,0)) |
ψ(Ω3×ψ(Ω2)) |
| ηη0 |
φ(3,φ(3,0)) |
ψ(Ω3×ψ(Ω3)) |
| ηη1 |
φ(3,φ(3,1)) |
ψ(Ω3×ψ(Ω3×2)) |
| ηηη0 |
φ(3,φ(3,φ(3,0))) |
ψ(Ω3×ψ(Ω3×ψ(Ω3))) |
| ηηηη0 |
φ(3,φ(3,φ(3,φ(3,0)))) |
ψ(Ω3×ψ(Ω3×ψ(Ω3×ψ(Ω3)))) |
| 4Ɛ0 |
φ(4,0) = φ(3,φ(3,φ(3,φ(3,...))) |
ψ(Ω4) = ψ(Ω3×ψ(Ω3×ψ(Ω3×ψ(...)))) |
| 5Ɛ0 |
φ(5,0) = φ(4,φ(4,φ(4,φ(4,...))) |
ψ(Ω5) = ψ(Ω4×ψ(Ω4×ψ(Ω4×ψ(...)))) |
| ωƐ0 |
φ(ω,0) |
ψ(Ωω) |
| 0ƐωƐ0+1 |
φ(φ(ω,0)+1) = ωφ(ω,0)+1 |
ψ(Ωω+1) |
| 0Ɛ0ƐωƐ0+1 |
φ(φ(φ(ω,0)+1)) = ωωφ(ω,0)+1 |
ψ(Ωω+ψ(Ωω+1)) |
| 1ƐωƐ0+1 |
φ(1,φ(ω,0)+1) = εφ(ω,0)+1 |
ψ(Ωω+Ω) |
| 1Ɛ1ƐωƐ0+1 |
φ(1,φ(1,φ(ω,0)+1)) = εεφ(ω,0)+1 |
ψ(Ωω+Ω×ψ(Ωω+Ω)) |
| 2ƐωƐ0+1 |
φ(2,φ(ω,0)+1) = ζφ(ω,0)+1 |
ψ(Ωω+Ω2) |
| 2Ɛ2ƐωƐ0+1 |
φ(2,φ(2,φ(ω,0)+1)) = ζζφ(ω,0)+1 |
ψ(Ωω+Ω2×ψ(Ωω+Ω2)) |
| 3ƐωƐ0+1 |
φ(3,φ(ω,0)+1) = ηφ(ω,0)+1 |
ψ(Ωω+Ω3) |
| ωƐ1 |
φ(ω,1) |
ψ(Ωω×2) = ψ(Ωω+Ωω) |
| ωƐ2 |
φ(ω,2) |
ψ(Ωω×3) |
| ωƐω |
φ(ω,ω) = φ(φ(1),φ(1)) |
ψ(Ωω×ω) = ψ(Ωω×ψ(1)) |
| ωƐω+1 |
φ(ω,ω+1) = φ(φ(1),φ(1)+1) |
ψ(Ωω×(ω+1)) = ψ(Ωω×(ψ(1)+1)) = ψ(Ωω×ω+Ωω) |
| ωƐωω |
φ(ω,ωω) = φ(φ(1),φ(φ(1))) |
ψ(Ωω×(ωω)) = ψ(Ωω×ψ(ψ(1))) |
| ωƐε0 |
φ(ω,ε0) = φ(φ(1),φ(1,0)) |
ψ(Ωω×ε0) = ψ(Ωω×ψ(Ω)) |
| ωƐζ0 |
φ(ω,ζ0) = φ(φ(1),φ(2,0)) |
ψ(Ωω×ζ0) = ψ(Ωω×ψ(Ω2)) |
| ωƐη0 |
φ(ω,η0) = φ(φ(1),φ(3,0)) |
ψ(Ωω×η0) = ψ(Ωω×ψ(Ω3)) |
| ωƐωƐ0 |
φ(ω,φ(ω,0)) |
ψ(Ωω×ψ(Ωω)) |
| ωƐωƐ0+1 |
φ(ω,φ(ω,0)+1) |
ψ(Ωω×ψ(Ωω)+Ωω) |
| ωƐωƐ0+ω |
φ(ω,φ(ω,0)+ω) |
ψ(Ωω×ψ(Ωω)+Ωω×ω) |
| ωƐωƐ0+ε0 |
φ(ω,φ(ω,0)+φ(1,0)) |
ψ(Ωω×ψ(Ωω)+Ωω×ψ(Ω)) |
| ωƐωƐ0×2 |
φ(ω,φ(ω,0)+φ(ω,0)) |
ψ(Ωω×ψ(Ωω)+Ωω×ψ(Ωω)) |
| ωƐωƐ0×ω |
φ(ω,φ(φ(ω,0)+1)) |
ψ(Ωω×ψ(Ωω+1)) |
| ωƐωƐ02 |
φ(ω,φ(φ(ω,0)+φ(ω,0))) |
ψ(Ωω×ψ(Ωω+ψ(Ωω×ψ(Ωω)))) |
| ƐωƐ0ω |
φ(ω,φ(φ(φ(ω,0)+1))) |
ψ(Ωω×ψ(Ωω+ψ(Ωω×ψ(Ωω+1)))) |
| ωƐ1ƐωƐ0+1 |
φ(ω,φ(1,φ(ω,0)+1)) |
ψ(Ωω×ψ(Ωω+Ω)) |
| ωƐ2ƐωƐ0+1 |
φ(ω,φ(2,φ(ω,0)+1)) |
ψ(Ωω×ψ(Ωω+Ω2)) |
| ωƐ3ƐωƐ0+1 |
φ(ω,φ(3,φ(ω,0)+1)) |
ψ(Ωω×ψ(Ωω+Ω3)) |
| ωƐωƐ1 |
φ(ω,φ(ω,1)) |
ψ(Ωω×ψ(Ωω+Ωω)) |
| ωƐωƐω |
φ(ω,φ(ω,ω)) |
ψ(Ωω×ψ(Ωω×ω)) |
| ωƐωƐωƐ0 |
φ(ω,φ(ω,φ(ω,0))) |
ψ(Ωω×ψ(Ωω×ψ(Ωω))) |
| ωƐωƐωƐ1 |
φ(ω,φ(ω,φ(ω,1))) |
ψ(Ωω×ψ(Ωω×ψ(Ωω+Ωω))) |
| ωƐωƐωƐω |
φ(ω,φ(ω,φ(ω,ω))) |
ψ(Ωω×ψ(Ωω×ψ(Ωω×ω))) |
| ωƐωƐωƐωƐ0 |
φ(ω,φ(ω,φ(ω,φ(ω,0)))) |
ψ(Ωω×ψ(Ωω×ψ(Ωω×ψ(Ωω)))) |
| ω+1Ɛ0 |
φ(ω+1,0) = φ(ω,φ(ω,φ(ω,...))) |
ψ(Ωω+1) = ψ(Ωω×Ω) = ψ(Ωω×ψ(Ωω×ψ(...))) |
| 1Ɛω+1Ɛ0+1 |
φ(1,φ(ω+1,0)+1) |
ψ(Ωω+1+Ω) |
| 2Ɛω+1Ɛ0+1 |
φ(2,φ(ω+1,0)+1) |
ψ(Ωω+1+Ω2) |
| ωƐω+1Ɛ0+1 |
φ(ω,φ(ω+1,0)+1) |
ψ(Ωω+1+Ωω) |
| ω+1Ɛ1 |
φ(ω+1,1) = φ(ω,φ(ω,φ(ω,...φ(ω+1,0)+1...))) |
ψ(Ωω+1×2) = ψ(Ωω+1+Ωω+1) = ψ(Ωω+1+Ωω×Ω) =
ψ(Ωω+1+Ωω×ψ(Ωω+1+Ωω×ψ(Ωω+1+Ωω×...))) |
| ω+1Ɛω |
φ(ω+1,ω) |
ψ(Ωω+1×ω) = ψ(Ωω+1×ψ(1)) |
| ω+1ƐωƐ0 |
φ(ω+1,φ(ω,0)) |
ψ(Ωω+1×ψ(Ωω)) |
| ω+1Ɛω+1Ɛ0 |
φ(ω+1,φ(ω+1,0)) |
ψ(Ωω+1×ψ(Ωω+1)) |
| ω+1Ɛω+1Ɛ1 |
φ(ω+1,φ(ω+1,1)) |
ψ(Ωω+1×ψ(Ωω+1×2)) |
| ω+1Ɛω+1Ɛω |
φ(ω+1,φ(ω+1,ω)) |
ψ(Ωω+1×ψ(Ωω+1×ω)) |
| ω+1Ɛω+1ƐωƐ0 |
φ(ω+1,φ(ω+1,φ(ω,0))) |
ψ(Ωω+1×ψ(Ωω+1×ψ(Ωω))) |
| ω+1Ɛω+1Ɛω+1Ɛ0 |
φ(ω+1,φ(ω+1,φ(ω+1,0))) |
ψ(Ωω+1×ψ(Ωω+1×ψ(Ωω+1))) |
| ω+2Ɛ0 |
φ(ω+2,0) = φ(ω+1,φ(ω+1,φ(ω+1,...))) |
ψ(Ωω+2) = ψ(Ωω+1×ψ(Ωω+1×ψ(...))) |
| ω+3Ɛ0 |
φ(ω+3,0) = φ(ω+2,φ(ω+2,φ(ω+2,...))) |
ψ(Ωω+3) = ψ(Ωω+2×ψ(Ωω+2×ψ(...))) |
| ω×2Ɛ0 |
φ(ω×2,0) |
ψ(Ωω×2) |
| ω×2Ɛ1 |
φ(ω×2,1) |
ψ(Ωω×2×2) |
| ω×2Ɛ2 |
φ(ω×2,2) |
ψ(Ωω×2×3) |
| ω×2Ɛω |
φ(ω×2,ω) |
ψ(Ωω×2×ω) |
| ω×2+1Ɛω |
φ(ω×2+1,0) = φ(ω×2,φ(ω×2,φ(ω×2,...))) |
ψ(Ωω×2+1) = ψ(Ωω×2×ψ(Ωω×2×ψ(...))) |
| ω×3Ɛ0 |
φ(ω×3,0) |
ψ(Ωω×3) |
| ω×4Ɛ0 |
φ(ω×4,0) |
ψ(Ωω×4) |
| ω2Ɛ0 |
φ(ω2,0) |
ψ(Ωω2) |
| ω3Ɛ0 |
φ(ω3,0) |
ψ(Ωω3) |
| ωωƐ0 |
φ(ωω,0) |
ψ(Ωωω) |
| ωωωƐ0 |
φ(ωωω,0) |
ψ(Ωωωω) |
| ωωωωƐ0 |
φ(ωωωω,0) |
ψ(Ωωωωω) |
| ωωωωωƐ0 |
φ(ωωωωω,0) |
ψ(Ωωωωωω) |
| 1Ɛ0Ɛ0 |
φ(ε0,0) = φ(φ(1,0),0) |
ψ(Ωψ(Ω)) |
| 1Ɛ1Ɛ0 |
φ(ε1,0) = φ(φ(1,1),0) |
ψ(Ωψ(Ω×2)) |
| 2Ɛ0Ɛ0 |
φ(ζ0,0) = φ(φ(2,0),0) |
ψ(Ωψ(Ω2)) |
| 3Ɛ0Ɛ0 |
φ(η0,0) = φ(φ(3,0),0) |
ψ(Ωψ(Ω3)) |
| 4Ɛ0Ɛ0 |
φ(φ(4,0),0) |
ψ(Ωψ(Ω4)) |
| ωƐ0Ɛ0 |
φ(φ(ω,0),0) |
ψ(Ωψ(Ωω)) |
| ω+1Ɛ0Ɛ0 |
φ(φ(ω+1,0),0) |
ψ(Ωψ(Ωω+1)) |
| ω×2Ɛ0Ɛ0 |
φ(φ(ω×2,0),0) |
ψ(Ωψ(Ωω×2)) |
| ω2Ɛ0Ɛ0 |
φ(φ(ω2,0),0) |
ψ(Ωψ(Ωω2)) |
| ωωƐ0Ɛ0 |
φ(φ(ωω,0),0) |
ψ(Ωψ(Ωωω)) |
| 1Ɛ0Ɛ0Ɛ0 |
φ(φ(ε0,0),0) |
ψ(Ωψ(Ωψ(Ω))) |
| 2Ɛ0Ɛ0Ɛ0 |
φ(φ(ζ0,0),0) |
ψ(Ωψ(Ωψ(Ω2))) |
| 3Ɛ0Ɛ0Ɛ0 |
φ(φ(η0,0),0) |
ψ(Ωψ(Ωψ(Ω3))) |
| ωƐ0Ɛ0Ɛ0 |
φ(φ(φ(ω,0),0),0) |
ψ(Ωψ(Ωψ(Ωω))) |
| 1Ɛ0Ɛ0Ɛ0Ɛ0 |
φ(φ(φ(ε0,0),0),0) |
ψ(Ωψ(Ωψ(Ωψ(Ω)))) |
| ωƐ0Ɛ0Ɛ0Ɛ0 |
φ(φ(φ(φ(ω,0),0),0),0) |
ψ(Ωψ(Ωψ(Ωψ(Ωω)))) |
| 1Ɛ0Ɛ0Ɛ0Ɛ0Ɛ0 |
φ(φ(φ(φ(ε0,0),0),0),0) |
ψ(Ωψ(Ωψ(Ωψ(Ωψ(Ω))))) |
| Г0 |
φ(1,0,0) = φ(φ(φ(φ(φ(...,0),0),0),0),0) |
ψ(ΩΩ) = ψ(Ωψ(Ωψ(Ωψ(Ωψ(...))))) |
| Г0+1 |
φ(1,0,0)+1 |
ψ(ΩΩ)+1 |
| Г0+ω |
φ(1,0,0)+φ(1) |
ψ(ΩΩ)+ψ(1) |
| Г0+ε0 |
φ(1,0,0)+φ(1,0) |
ψ(ΩΩ)+ψ(Ω) |
| Г0×2 |
φ(1,0,0)+φ(1,0,0) |
ψ(ΩΩ)+ψ(ΩΩ) |
| ωГ0+1 |
φ(Г0+1) = φ(φ(1,0,0)+1) |
ψ(ΩΩ+1) |
| ωГ0×2 |
φ(Г0+Г0) |
ψ(ΩΩ+ψ(ΩΩ)) |
| ωωГ0+1 |
φ(φ(Г0+1)) |
ψ(ΩΩ+ψ(ΩΩ+1)) |
| ωωГ0×2 |
φ(φ(Г0×2)) |
ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ)) |
| ωωωГ0+1 |
φ(φ(φ(Г0+1))) |
ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ+1))) |
| ωωωГ0×2 |
φ(φ(φ(Г0×2))) |
ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ)))) |
| ωωωωГ0+1 |
φ(φ(φ(φ(Г0+1)))) |
ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ+1)))) |
| εГ0+1 |
φ(1,Г0+1) = φ(φ(φ(φ(...φ(1,0,0)+1...)))) |
ψ(ΩΩ+Ω) = ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ+...)))) |
| ζГ0+1 |
φ(2,Г0+1) |
ψ(ΩΩ+Ω2) |
| ηГ0+1 |
φ(3,Г0+1) |
ψ(ΩΩ+Ω3) |
| ωƐГ0+1 |
φ(ω,Г0+1) |
ψ(ΩΩ+Ωω) |
| ωƐ0ƐГ0+1 |
φ(φ(ω,0),Г0+1) |
ψ(ΩΩ+Ωψ(Ωω)) |
| ωωƐ0ƐГ0+1 |
φ(φ(ωω,0),Г0+1) |
ψ(ΩΩ+Ωψ(Ωωω)) |
| 1Ɛ0Ɛ0ƐГ0+1 |
φ(φ(ε0,0),Г0+1) |
ψ(ΩΩ+Ωψ(Ωψ(Ω))) |
| 2Ɛ0Ɛ0ƐГ0+1 |
φ(φ(ζ0,0),Г0+1) |
ψ(ΩΩ+Ωψ(Ωψ(Ω2))) |
| ωƐ0Ɛ0ƐГ0+1 |
φ(φ(φ(ω,0),0),Г0+1) |
ψ(ΩΩ+Ωψ(Ωψ(Ωω))) |
| ωƐ0Ɛ0Ɛ0ƐГ0+1 |
φ(φ(φ(φ(ω,0),0),0),Г0+1) |
ψ(ΩΩ+Ωψ(Ωψ(Ωω))) |
| Г0Ɛ1 |
φ(Г0,1) = φ(φ(φ(...,0),0),Г0+1) |
ψ(ΩΩ+Ωψ(ΩΩ)) = ψ(ΩΩ+Ωψ(Ωψ(Ωψ(Ω...)))) |
| ωГ0Ɛ1+1 |
φ(φ(Г0,1)+1) |
ψ(ΩΩ+Ωψ(ΩΩ)+1) |
| εГ0Ɛ1+1 |
φ(1,φ(Г0,1)+1) |
ψ(ΩΩ+Ωψ(ΩΩ)+Ω) |
| ζГ0Ɛ1+1 |
φ(2,φ(Г0,1)+1) |
ψ(ΩΩ+Ωψ(ΩΩ)+Ω2) |
| ηГ0Ɛ1+1 |
φ(3,φ(Г0,1)+1) |
ψ(ΩΩ+Ωψ(ΩΩ)+Ω3) |
| ωƐГ0Ɛ1+1 |
φ(ω,φ(Г0,1)+1) |
ψ(ΩΩ+Ωψ(ΩΩ)+Ωω) |
| ωƐ0ƐГ0Ɛ1+1 |
φ(φ(ω,0),φ(Г0,1)+1) |
ψ(ΩΩ+Ωψ(ΩΩ)+Ωψ(Ωω)) |
| ωƐ0Ɛ0ƐГ0Ɛ1+1 |
φ(φ(φ(ω,0),0),φ(Г0,1)+1) |
ψ(ΩΩ+Ωψ(ΩΩ)+Ωψ(Ωψ(Ωω))) |
| ωƐ0Ɛ0Ɛ0ƐГ0Ɛ1+1 |
φ(φ(φ(φ(ω,0),0),0),φ(Г0,1)+1) |
ψ(ΩΩ+Ωψ(ΩΩ)+Ωψ(Ωψ(Ωψ(Ωω)))) |
| Г0Ɛ2 |
φ(Г0,2) |
ψ(ΩΩ+Ωψ(ΩΩ)×2) = ψ(ΩΩ+Ωψ(ΩΩ)+Ωψ(Ωψ(Ωψ(Ω...)))) |
| Г0Ɛ3 |
φ(Г0,3) |
ψ(ΩΩ+Ωψ(ΩΩ)×3) |
| Г0Ɛω |
φ(Г0,ω) |
ψ(ΩΩ+Ωψ(ΩΩ)×ω) |
| Г0Ɛε0 |
φ(Г0,ε0) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(Ω)) |
| Г0Ɛζ0 |
φ(Г0,ζ0) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(Ω2)) |
| Г0Ɛη0 |
φ(Г0,η0) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(Ω3)) |
| Г0ƐωƐ0 |
φ(Г0,φ(ω,0)) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(Ωω)) |
| Г0ƐωƐ0Ɛ0 |
φ(Г0,φ(φ(ω,0),0)) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(Ωψ(Ωω))) |
| Г0ƐωƐ0Ɛ0Ɛ0 |
φ(Г0,φ(φ(φ(ω,0),0),0)) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(Ωψ(Ωψ(Ωω)))) |
| Г0ƐωƐ0Ɛ0Ɛ0Ɛ0 |
φ(Г0,φ(φ(φ(φ(ω,0),0),0),0)) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(Ωψ(Ωψ(Ωψ(Ωω))))) |
| Г0ƐГ0 |
φ(Г0,Г0) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ)) |
| Г0ƐГ0+1 |
φ(Г0,Г0+1) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ)+Ωψ(ΩΩ))) |
| Г0ƐГ0×2 |
φ(Г0,Г0+Г0) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ)+Ωψ(ΩΩ)×ψ(ΩΩ))) |
| Г0ƐωГ0+1 |
φ(Г0,φ(Г0+1)) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+1))) |
| Г0ƐωГ0×2 |
φ(Г0,φ(Г0+Г0)) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+ψ(ΩΩ)))) |
| Г0ƐωωГ0+1 |
φ(Г0,φ(φ(Г0+1))) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+ψ(ΩΩ+1)))) |
| Г0ƐεГ0+1 |
φ(Г0,φ(1,Г0+1)) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ω))) |
| Г0ƐГ0Ɛ1 |
φ(Г0,φ(Г0,1)) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ωψ(ΩΩ)))) |
| Г0ƐГ0ƐГ0 |
φ(Г0,φ(Г0,Г0)) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ)) |
| Г0ƐГ0ƐГ0Ɛ1 |
φ(Г0,φ(Г0,φ(Г0,1))) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ωψ(ΩΩ))))) |
| Г0ƐГ0ƐГ0ƐГ0 |
φ(Г0,φ(Г0,φ(Г0,Г0))) |
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ))))) |
| Г0+1Ɛ0 |
φ(Г0+1,0) = φ(Г0,φ(Г0,φ(Г0,φ(Г0,...)))) |
ψ(ΩΩ+Ωψ(ΩΩ)+1) = ψ(ΩΩ+Ωψ(ΩΩ)×Ω) =
ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ωψ(ΩΩ)×ψ(ΩΩ+Ωψ(ΩΩ)×...))) |
| ωГ0+1Ɛ0+1 |
φ(φ(Г0+1,0)+1) |
ψ(ΩΩ+Ωψ(ΩΩ)+1+1) |
| εГ0+1Ɛ0+1 |
φ(1,φ(Г0+1,0)+1) |
ψ(ΩΩ+Ωψ(ΩΩ)+1+Ω) |
| Г0ƐГ0+1Ɛ0+1 |
φ(Г0,φ(Г0+1,0)+1) |
ψ(ΩΩ+Ωψ(ΩΩ)+1+Ωψ(ΩΩ)) |
| Г0+1Ɛ1 |
φ(Г0+1,1) = φ(Г0,φ(Г0,φ(Г0,...φ(Г0+1,0)+1...))) |
ψ(ΩΩ+Ωψ(ΩΩ)+1×2) |
| Г0+1ƐГ0 |
φ(Г0+1,Г0) |
ψ(ΩΩ+Ωψ(ΩΩ)+1×ψ(ΩΩ)) |
| Г0+2Ɛ0 |
φ(Г0+2,0) |
ψ(ΩΩ+Ωψ(ΩΩ)+2) = ψ(ΩΩ+Ωψ(ΩΩ)+1×Ω) =
ψ(ΩΩ+Ωψ(ΩΩ)+1×ψ(ΩΩ+Ωψ(ΩΩ)+1×...)) |
| Г0+ωƐ0 |
φ(Г0+ω,0) |
ψ(ΩΩ+Ωψ(ΩΩ)+ω) |
| Г0+ε0Ɛ0 |
φ(Г0+ε0,0) |
ψ(ΩΩ+Ωψ(ΩΩ)+ψ(Ω)) |
| Г0+ωƐ0Ɛ0 |
φ(Г0+φ(ω,0),0) |
ψ(ΩΩ+Ωψ(ΩΩ)+ψ(Ωω)) |
| Г0+Г0Ɛ0 |
φ(Г0×2,0) |
ψ(ΩΩ+Ωψ(ΩΩ)+ψ(ΩΩ)) |
| ωГ0+1Ɛ0 |
φ(φ(Г0+1),0) |
ψ(ΩΩ+Ωψ(ΩΩ+1)) = ψ(ΩΩ+Ωψ(ΩΩ)×ω) |
| ωωГ0+1Ɛ0 |
φ(φ(Г0+1),0) |
ψ(ΩΩ+Ωψ(ΩΩ+ψ(ΩΩ+1))) |
| εГ0+1Ɛ0 |
φ(φ(1,Г0+1),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ω)) |
| ζГ0+1Ɛ0 |
φ(φ(2,Г0+1),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ω2)) |
| ηГ0+1Ɛ0 |
φ(φ(3,Г0+1),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ω3)) |
| ωƐГ0+1Ɛ0 |
φ(φ(ω,Г0+1),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωω)) |
| ωƐ0ƐГ0+1Ɛ0 |
φ(φ(φ(ω,0),Г0+1),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(Ωω))) |
| Г0Ɛ1Ɛ0 |
φ(φ(Г0,1),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ))) |
| Г0Ɛ1Ɛ1 |
φ(φ(Г0,1),1) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ))×2) |
| Г0Ɛ1Ɛω |
φ(φ(Г0,1),ω) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ))×ω) |
| Г0Ɛ1+1Ɛ0 |
φ(φ(Г0,1)+1,0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ))+1) = ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ))×Ω) |
| Г0Ɛ1+Г0Ɛ1Ɛ0 |
φ(φ(Г0,1)×2,0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ))×2) |
| 0ƐГ0Ɛ1+1Ɛ0 |
φ(φ(φ(Г0,1)+1),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)+1)) = ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ))×ω) |
| 1ƐГ0Ɛ1+1Ɛ0 |
φ(φ(1,φ(Г0,1)+1),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)+Ω)) |
| ωƐГ0Ɛ1+1Ɛ0 |
φ(φ(ω,φ(Г0,1)+1),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)+Ωω)) |
| Г0Ɛ2Ɛ0 |
φ(φ(Г0,2),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)×2)) |
| Г0ƐωƐ0 |
φ(φ(Г0,ω),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)×ω)) |
| Г0+1Ɛ0Ɛ0 |
φ(φ(Г0+1,0),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)+1)) = ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)×Ω)) |
| Г0+Г0Ɛ0Ɛ0 |
φ(φ(Г0+Г0,0),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)+ψ(ΩΩ))) |
| 0ƐГ0+1Ɛ0Ɛ0 |
φ(φ(φ(Г0+1,0)),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ+1))) = ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)×ω)) |
| 1ƐГ0+1Ɛ0Ɛ0 |
φ(φ(φ(1,Г0+1),0),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ+Ω))) |
| ωƐГ0+1Ɛ0Ɛ0 |
φ(φ(φ(ω,Г0+1),0),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ+Ωω))) |
| Г0Ɛ1Ɛ0Ɛ0 |
φ(φ(φ(Г0,1),0),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)))) |
| Г0+1Ɛ0Ɛ0Ɛ0 |
φ(φ(φ(Г0+1,0),0),0) |
ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)+1))) |
| Г1 |
φ(1,0,1) = φ(φ(φ(...φ(Г0+1,0)...,0),0),0) |
ψ(ΩΩ×2) = ψ(ΩΩ+ΩΩ) = ψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ+Ωψ(ΩΩ)+...))) |
| 1ƐГ1+1 |
φ(1,Г1+1) |
ψ(ΩΩ×2+Ω) |
| ωƐГ1+1 |
φ(ω,Г1+1) |
ψ(ΩΩ×2+Ωω) |
| Г0ƐГ1+1 |
φ(Г0,Г1+1) |
ψ(ΩΩ×2+Ωψ(ΩΩ)) |
| Г1Ɛ1 |
φ(Г1,1) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2)) |
| Г1Ɛ2 |
φ(Г1,2) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2)×2) |
| Г1ƐГ0 |
φ(Г1,Г0) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2)×ψ(ΩΩ)) |
| Г1ƐГ1 |
φ(Г1,Г1) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2)×ψ(ΩΩ×2)) |
| Г1+1Ɛ0 |
φ(Г1+1,0) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2)+1) = ψ(ΩΩ×2+Ωψ(ΩΩ×2)×Ω) |
| Г1+Г0Ɛ0 |
φ(Г1+Г0,0) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2)+ψ(ΩΩ)) |
| Г1+Г1Ɛ0 |
φ(Г1×2,0) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2)×2) |
| ωГ1+1Ɛ0 |
φ(φ(Г1+1),0) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2+1)) = ψ(ΩΩ×2+Ωψ(ΩΩ×2)×ω) |
| ωωГ1+1Ɛ0 |
φ(φ(φ(Г1+1)),0) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2+ψ(ΩΩ×2+1))) |
| 1ƐГ1+1Ɛ0 |
φ(φ(1,Г1+1),0) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2+Ω)) |
| 2ƐГ1+1Ɛ0 |
φ(φ(2,Г1+1),0) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2+Ω2)) |
| Г0ƐГ1+1Ɛ0 |
φ(φ(Г0,Г1+1),0) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2+Ωψ(ΩΩ))) |
| Г1Ɛ1Ɛ0 |
φ(φ(Г1,1),0) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2+Ωψ(ΩΩ×2))) |
| Г1Ɛ1Ɛ0Ɛ0 |
φ(φ(φ(Г1,1),0),0) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2+Ωψ(ΩΩ×2+Ωψ(ΩΩ×2)))) |
| Г2 |
φ(1,0,2) |
ψ(ΩΩ×3) = ψ(ΩΩ×2+Ωψ(ΩΩ×2+Ωψ(ΩΩ×2+Ωψ(ΩΩ×2+...)))) |
| Гω |
φ(1,0,φ(1)) |
ψ(ΩΩ×ω) |
| Гε0 |
φ(1,0,φ(1,0)) |
ψ(ΩΩ×ψ(Ω)) |
| ГωƐ0 |
φ(1,0,φ(φ(1),0)) |
ψ(ΩΩ×ψ(Ωω)) |
| Г1Ɛ0Ɛ0 |
φ(1,0,φ(φ(1,0),0)) |
ψ(ΩΩ×ψ(Ωψ(Ω))) |
| ГωƐ0Ɛ0 |
φ(1,0,φ(φ(φ(1),0),0)) |
ψ(ΩΩ×ψ(Ωψ(Ωω))) |
| ГГ0 |
φ(1,0,φ(1,0,0)) |
ψ(ΩΩ×ψ(ΩΩ)) |
| ГГ1 |
φ(1,0,φ(1,0,1)) |
ψ(ΩΩ×ψ(ΩΩ×2)) |
| ГГГ0 |
φ(1,0,φ(1,0,φ(1,0,0))) |
ψ(ΩΩ×ψ(ΩΩ×ψ(ΩΩ)) |
| ГГГГ0 |
φ(1,0,φ(1,0,φ(1,0,φ(1,0,0)))) |
ψ(ΩΩ×ψ(ΩΩ×ψ(ΩΩ×ψ(ΩΩ))) |
| 1Г0 |
φ(1,1,0) = φ(1,0,φ(1,0,φ(1,0,φ(1,0,...)))) |
ψ(ΩΩ×Ω) = ψ(ΩΩ+1) = ψ(ΩΩ×ψ(ΩΩ×ψ(ΩΩ×...)) |
| ω1Г0+1 |
φ(φ(1,1,0)+1) |
ψ(ΩΩ+1+1) |
| 1Ɛ1Г0+1 |
φ(1,φ(1,1,0)+1) |
ψ(ΩΩ+1+Ω) |
| Г0Ɛ1Г0+1 |
φ(φ(1,0,0),φ(1,1,0)+1) |
ψ(ΩΩ+1+Ωψ(ΩΩ)) |
| Г1Ɛ1Г0+1 |
φ(φ(1,0,1),φ(1,1,0)+1) |
ψ(ΩΩ+1+Ωψ(ΩΩ×2)) |
| 1Г0Ɛ1 |
φ(φ(1,1,0),1) |
ψ(ΩΩ+1+Ωψ(ΩΩ+1)) |
| 1Г0+1Ɛ0 |
φ(φ(1,1,0)+1,0) |
ψ(ΩΩ+1+Ωψ(ΩΩ+1)+1) |
| ω1Г0+1Ɛ0 |
φ(φ(φ(1,1,0)+1),0) |
ψ(ΩΩ+1+Ωψ(ΩΩ+1+1)) |
| 1Ɛ1Г0+1Ɛ0 |
φ(φ(1,φ(1,1,0)+1),0) |
ψ(ΩΩ+1+Ωψ(ΩΩ+1+Ω)) |
| Г0Ɛ1Г0+1Ɛ0 |
φ(φ(φ(1,0,0),φ(1,1,0)+1),0) |
ψ(ΩΩ+1+Ωψ(ΩΩ+1+Ωψ(ΩΩ))) |
| 1Г0Ɛ1Ɛ0 |
φ(φ(φ(1,1,0),1),0) |
ψ(ΩΩ+1+Ωψ(ΩΩ+1+Ωψ(ΩΩ+1))) |
| 1Г0+1Ɛ0Ɛ0 |
φ(φ(φ(1,1,0)+1,0),0) |
ψ(ΩΩ+1+Ωψ(ΩΩ+1+Ωψ(ΩΩ+1)+1)) |
| Г1Г0+1 |
φ(1,0,φ(1,1,0)+1) |
ψ(ΩΩ+1+ΩΩ) = ψ(ΩΩ+1+Ωψ(ΩΩ+1+Ωψ(ΩΩ+1+...))) |
| Г1Г0+2 |
φ(1,0,φ(1,1,0)+2) |
ψ(ΩΩ+1+ΩΩ×2) |
| Г1Г0×2 |
φ(1,0,φ(1,1,0)+φ(1,1,0)) |
ψ(ΩΩ+1+ΩΩ×ψ(ΩΩ+1)) |
| Гω1Г0+1 |
φ(1,0,φ(φ(1,1,0)+1)) |
ψ(ΩΩ+1+ΩΩ×ψ(ΩΩ+1+1)) = ψ(ΩΩ+1+ΩΩ×ψ(ΩΩ+1)×ω) |
| 0Г1Ɛ1Г0+1 |
φ(1,0,φ(1,φ(1,1,0)+1)) |
ψ(ΩΩ+1+ΩΩ×ψ(ΩΩ+1+Ω)) |
| 0Г0Г1Г0+1 |
φ(1,0,φ(1,0,φ(1,1,0)+1)) |
ψ(ΩΩ+1+ΩΩ×ψ(ΩΩ+1+ΩΩ)) |
| 1Г1 |
φ(1,1,1) = φ(1,0,φ(1,0,φ(1,0,...φ(1,1,0)+1...))) |
ψ(ΩΩ+1×2) = ψ(ΩΩ+1+ΩΩ×ψ(ΩΩ+1+ΩΩ×...)) |
| 2Г0 |
φ(1,2,0) = φ(1,1,φ(1,1,φ(1,1,φ(1,1,...)))) |
ψ(ΩΩ+2) |
| ωГ0 |
φ(1,ω,0) = φ(1,φ(1),0) |
ψ(ΩΩ+ω) |
| ωωГ0 |
φ(1,ωω,0) = φ(1,φ(φ(1)),0) |
ψ(ΩΩ+ωω) |
| 1Ɛ0Г0 |
φ(1,ε0,0) = φ(1,φ(1,0),0) |
ψ(ΩΩ+ψ(Ω)) |
| Г0Г0 |
φ(1,Г0,0) = φ(1,φ(1,0,0),0) |
ψ(ΩΩ+ψ(ΩΩ)) |
| Г1Г0 |
φ (1,Г1,0) = φ(1,φ(1,0,1),0) |
ψ(ΩΩ+ψ(ΩΩ×2)) |
| 1Г0Г0 |
φ(1,φ(1,1,0),0) = φ(1,φ(1,0,φ(1,0,φ(1,0,...))),0) |
ψ(ΩΩ+ψ(ΩΩ+1)) |
| ωГ0Г0 |
φ(1,φ(1,φ(1),0),0) |
ψ(ΩΩ+ψ(ΩΩ+ω)) |
| ε0Г0Г0 |
φ(1,φ(1,φ(1,0),0),0) |
ψ(ΩΩ+ψ(ΩΩ+ψ(Ω))) |
| Г0Г0Г0 |
φ(1,φ(1,φ(1,0,0),0),0) |
ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ))) |
| Г0Г0Г0Г0 |
φ(1,φ(1,φ(1,φ(1,0,0),0),0),0) |
ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ)))) |
| P0 |
φ(2,0,0) = φ(1,φ(1,φ(1,φ(1,...,0),0),0),0) |
ψ(ΩΩ×2) = ψ(ΩΩ+Ω) = ψ(ΩΩ+ψ(ΩΩ+ψ(ΩΩ+...))) |
| ωP0+1 |
φ(φ(2,0,0)+1) |
ψ(ΩΩ×2+1) |
| 1ƐP0+1 |
φ(1,φ(2,0,0)+1) |
ψ(ΩΩ×2+Ω) |
| Г0ƐP0+1 |
φ(φ(1,0,0),φ(2,0,0)+1) |
ψ(ΩΩ×2+Ωψ(ΩΩ)) |
| P0Ɛ1 |
φ(φ(2,0,0),1) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2)) |
| P0+1Ɛ0 |
φ(φ(2,0,0)+1,0) |
ψ(ΩΩ×2+Ωψ(ΩΩ×2)+1) |
| ГP0+1 |
φ(1,0,φ(2,0,0)+1) |
ψ(ΩΩ×2+ΩΩ) |
| 1ГP0+1 |
φ(1,1,φ(2,0,0)+1) |
ψ(ΩΩ×2+ΩΩ+1) |
| ωГP0+1 |
φ(1,ω,φ(2,0,0)+1) |
ψ(ΩΩ×2+ΩΩ+ω) |
| ε0ГP0+1 |
φ(1,ε0,φ(2,0,0)+1) |
ψ(ΩΩ×2+ΩΩ+ψ(Ω)) |
| Г0ГP0+1 |
φ(1,Г0,φ(2,0,0)+1) |
ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ)) |
| P0Г1 |
φ(1,φ(2,0,0),1) |
ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2)) |
| P0Г2 |
φ(1,φ(2,0,0),2) |
ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2)×2) |
| P0+1Г0 |
φ(1,φ(2,0,0)+1,0) |
ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2)+1) |
| ωP0+1Г0 |
φ(1,φ(φ(2,0,0)+1),0) |
ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2+1)) = ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2)×ω) |
| 1ƐP0+1Г0 |
φ(1,φ(1,φ(2,0,0)+1),0) |
ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2+Ω)) |
| ГP0+1Г0 |
φ(1,φ(1,0,φ(2,0,0)+1),0) |
ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2+ΩΩ)) |
| 1ГP0+1Г0 |
φ(1,φ(1,1,φ(2,0,0)+1),0) |
ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2+ΩΩ+1)) |
| P0Г1Г0 |
φ(1,φ(1,φ(2,0,0),1),0) |
ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2))) |
| P0+1Г0Г0 |
φ(1,φ(1,φ(2,0,0)+1,0),0) |
ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2)+1)) |
| P1 |
φ(2,0,1) |
ψ(ΩΩ×2×2) = ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2+ΩΩ+ψ(ΩΩ×2+...))) |
| 1P0 |
φ(2,1,0) |
ψ(ΩΩ×2×Ω) = ψ(ΩΩ×2+1) |
| B0 |
φ(3,0,0) |
ψ(ΩΩ×3) = ψ(ΩΩ×2+Ω) = ψ(ΩΩ×2+ψ(ΩΩ×2+ψ(ΩΩ×2+...))) |
| - |
φ(ω,0,0) |
ψ(ΩΩ×ω) |
| - |
φ(1,φ(ω,0,0)+1) |
ψ(ΩΩ×ω+Ω) |
| - |
φ(1,0,φ(ω,0,0)+1) |
ψ(ΩΩ×ω+ΩΩ) |
| - |
φ(2,0,φ(ω,0,0)+1) |
ψ(ΩΩ×ω+ΩΩ×2) |
| - |
φ(ω,0,1) |
ψ(ΩΩ×ω×2) |
| - |
φ(ω,1,0) |
ψ(ΩΩ×ω+1) = ψ(ΩΩ×ω×Ω) |
| - |
φ(ω+1,0,0) |
ψ(ΩΩ×ω+Ω) = ψ(ΩΩ×ω+ψ(ΩΩ×ω+ψ(ΩΩ×ω+...))) |
| - |
φ(ω×2,0,0) |
ψ(ΩΩ×ω×2) = ψ(ΩΩ×ω+Ω×ω) |
| - |
φ(ω2,0,0) |
ψ(ΩΩ×ω2) |
| - |
φ(ωω,0,0) |
ψ(ΩΩ×ωω) |
| - |
φ(ε0,0,0) |
ψ(ΩΩ×ψ(Ω)) |
| - |
φ(Г0,0,0) = φ(φ(1,0,0),0,0) |
ψ(ΩΩ×ψ(ΩΩ)) |
| - |
φ(φ(ω,0,0),0,0) |
ψ(ΩΩ×ψ(ΩΩ×ω)) |
| - |
φ(φ(φ(1,0,0),0,0),0,0) |
ψ(ΩΩ×ψ(ΩΩ×ψ(ΩΩ))) |
| - |
φ(φ(φ(ω,0,0),0,0),0,0) |
ψ(ΩΩ×ψ(ΩΩ×ψ(ΩΩ×ω))) |
| - |
φ(φ(φ(φ(1,0,0),0,0),0,0),0,0) |
ψ(ΩΩ×ψ(ΩΩ×ψ(ΩΩ×ψ(ΩΩ)))) |
| - |
φ(1,0,0,0) = φ(φ(φ(...,0,0),0,0),0,0) |
ψ(ΩΩ2) = ψ(ΩΩ×Ω) = ψ(ΩΩ×ψ(ΩΩ×ψ(ΩΩ×...))) |
| - |
φ(1,φ(1,0,0,0)+1) |
ψ(ΩΩ2+Ω) |
| - |
φ(1,0,φ(1,0,0,0)+1) |
ψ(ΩΩ2+ΩΩ) |
| - |
φ(1,0,0,1) |
ψ(ΩΩ2×2) |
| - |
φ(1,0,1,0) |
ψ(ΩΩ2+1) |
| - |
φ(1,1,0,0) |
ψ(ΩΩ2+Ω) |
| - |
φ(2,0,0,0) |
ψ(ΩΩ2×2) |
| - |
φ(ω,0,0,0) |
ψ(ΩΩ2×ω) |
| - |
φ(ωω,0,0,0) |
ψ(ΩΩ2×ωω) |
| - |
φ(φ(1,0,0,0),0,0,0) |
ψ(ΩΩ2×ψ(ΩΩ2)) |
| - |
φ(1,0,0,0,0) = φ(φ(φ(...,0,0,0),0,0,0),0,0,0) |
ψ(ΩΩ3) = ψ(ΩΩ2×Ω) = ψ(ΩΩ2×ψ(ΩΩ2×ψ(ΩΩ2×...))) |
| - |
φ(1,0,0,0,0,0) = φ(φ(φ(...,0,0,0,0),0,0,0,0),0,0,0,0) |
ψ(ΩΩ4) = ψ(ΩΩ3×Ω) = ψ(ΩΩ3×ψ(ΩΩ3×ψ(ΩΩ3×...))) |
| - |
φ(1,0,0,0,0,0,...) = sup(φ(1n)|n<ω) = φ(1ω) |
ψ(ΩΩω) |
| - |
φ(1ω)+1 |
ψ(ΩΩω)+1 |
| - |
φ(1ω)×2 |
ψ(ΩΩω)×2 |
| - |
φ(φ(1ω)+1) = ωφ(1ω)+1 = φ(1ω)×ω |
ψ(ΩΩω+1) |
| - |
φ(φ(1ω)+φ(1ω)) = ωφ(1ω)×2 = φ(1ω)2 |
ψ(ΩΩω+ψ(ΩΩω)) |
| - |
φ(φ(φ(1ω)+1)) = φ(1ω)ω |
ψ(ΩΩω+ψ(ΩΩω+1)) |
| - |
φ(1,φ(1ω)+1) = εφ(1ω)+1 |
ψ(ΩΩω+Ω) |
| - |
φ(2,φ(1ω)+1) = ζφ(1ω)+1 |
ψ(ΩΩω+Ω2) |
| - |
φ(ω,φ(1ω)+1) |
ψ(ΩΩω+Ωω) |
| - |
φ(Г0,φ(1ω)+1) = φ(φ(φ(φ(...,0),0),0),φ(1ω)+1) |
ψ(ΩΩω+Ωψ(ΩΩ)) |
| - |
φ(φ(1ω),1) = φ(φ(1,0,0,0,0,0,...),φ(1ω)+1) |
ψ(ΩΩω+Ωψ(ΩΩω)) |
| - |
φ(φ(1ω)+1,0) = φ(φ(1ω),φ(φ(1ω),φ(φ(1ω),...))) |
ψ(ΩΩω+Ωψ(ΩΩω)+1) = ψ(ΩΩω+Ωψ(ΩΩω)×Ω) |
| - |
φ(φ(φ(1ω)+1),0) = φ(φ(1ω)×ω,0) |
ψ(ΩΩω+Ωψ(ΩΩω+1)) = ψ(ΩΩω+Ωψ(ΩΩω)×ω) |
| - |
φ(φ(φ(1ω)+φ(1ω)),0) = φ(φ(1ω)2,0) |
ψ(ΩΩω+Ωψ(ΩΩω+ψ(ΩΩω))) |
| - |
φ(φ(φ(φ(1ω)+1)),0) = φ(φ(1ω)ω,0) |
ψ(ΩΩω+Ωψ(ΩΩω+ψ(ΩΩω+1))) |
| - |
φ(φ(φ(φ(1ω)+φ(1ω))),0) = φ(φ(1ω)φ(1ω),0) |
ψ(ΩΩω+Ωψ(ΩΩω+ψ(ΩΩω+ψ(ΩΩω)))) |
| - |
φ(φ(φ(φ(φ(1ω)+1))),0) = φ(φ(1ω)φ(1ω)ω,0) |
ψ(ΩΩω+Ωψ(ΩΩω+ψ(ΩΩω+ψ(ΩΩω+1)))) |
| - |
φ(φ(1,φ(1ω)+1),0) = φ(εφ(1ω)+1,0) |
ψ(ΩΩω+Ωψ(ΩΩω+Ω)) |
| - |
φ(φ(Г0,φ(1ω)+1),0) = φ(φ(φ(φ(...,0),0),φ(1ω)+1),0) |
ψ(ΩΩω+Ωψ(ΩΩω+Ωψ(ΩΩ))) |
| - |
φ(φ(φ(1ω),1),0) = φ(φ(φ(1,0,0,0,0,0,...),φ(1ω)+1),0) |
ψ(ΩΩω+Ωψ(ΩΩω+Ωψ(ΩΩω))) |
| - |
φ(1,0,φ(1ω)+1) = φ(φ(φ(...φ(φ(1ω),1)...,0),0),0) |
ψ(ΩΩω+ΩΩ) = ψ(ΩΩω+Ωψ(ΩΩω+Ωψ(ΩΩω+Ω...))) |
| - |
φ(1,1,φ(1ω)+1) = φ(1,0,φ(1,0,...φ(1,0,φ(1ω)+1)...)) |
ψ(ΩΩω+ΩΩ+1) |
| - |
φ(1,Г0,φ(1ω)+1) = φ(1,φ(φ(φ(...,0),0),0),φ(1ω)+1) |
ψ(ΩΩω+ΩΩ+ψ(ΩΩ)) |
| - |
φ(1,φ(1ω),1) = φ(1,φ(1,0,0,0,0,0,...),φ(1ω)+1) |
ψ(ΩΩω+ΩΩ+ψ(ΩΩω)) |
| - |
φ(2,0,φ(1ω)+1) = φ(1,φ(1,...φ(1,φ(1ω),1)...,0),0) |
ψ(ΩΩω+ΩΩ×2) = ψ(ΩΩω+ΩΩ+ψ(ΩΩω+ΩΩ+ψ(ΩΩω+...))) |
| - |
φ(ω,0,φ(1ω)+1) |
ψ(ΩΩω+ΩΩ×ω) |
| - |
φ(Г0,0,φ(1ω)+1) = φ(φ(φ(φ(...,0),0),0),0,φ(1ω)+1) |
ψ(ΩΩω+ΩΩ×ψ(ΩΩ)) |
| - |
φ(φ(1ω),0,1) = φ(φ(1,0,0,0,0,0,...),0,φ(1ω)+1) |
ψ(ΩΩω+ΩΩ×ψ(ΩΩω)) |
| - |
φ(1,0,0,φ(1ω)+1) = φ(φ(...φ(φ(1ω),0,1)...,0,0),0,0) |
ψ(ΩΩω+ΩΩ2) = ψ(ΩΩω+ΩΩ×ψ(ΩΩω+ΩΩ×ψ(ΩΩω+...))) |
| - |
φ(1ω10) = φ(φ(1ω),0,0,0,...,1) |
ψ(ΩΩω×2) = ψ(ΩΩω+ΩΩω) |
| - |
φ(1ω20) = φ(φ(1ω10),0,0,0,...,1) |
ψ(ΩΩω×3) |
| - |
φ(1ωω0) |
ψ(ΩΩω×ω) |
| - |
φ(1ωωω0) |
ψ(ΩΩω×ωω) |
| - |
φ(1ωε00) = φ(1ωφ(11)0) |
ψ(ΩΩω×ψ(Ω)) |
| - |
φ(1ωГ00) = φ(1ωφ(12)0) |
ψ(ΩΩω×ψ(ΩΩ)) |
| - |
φ(1ωφ(1ω)0) |
ψ(ΩΩω×ψ(ΩΩω)) |
| - |
φ(1ω11) = φ(1ωφ(1ωφ(1ω...0)0)0) |
ψ(ΩΩω+1) = ψ(ΩΩω×Ω) |
| - |
φ(1ω21) = φ(1ω11φ(1ω11φ(1ω11...0)0)0) |
ψ(ΩΩω+2) = ψ(ΩΩω+1×Ω) |
| - |
φ(1ωω1) |
ψ(ΩΩω+ω) |
| - |
φ(1ωωω1) |
ψ(ΩΩω+ωω) |
| - |
φ(1ωε01) = φ(1ωφ(11)1) |
ψ(ΩΩω+ψ(Ω)) |
| - |
φ(1ωГ01) = φ(1ωφ(12)1) |
ψ(ΩΩω+ψ(ΩΩ)) |
| - |
φ(1ω12) = φ(1ωφ(1ωφ(1ω...1)1)1) |
ψ(ΩΩω+Ω) = ψ(ΩΩω+ψ(ΩΩω+ψ(ΩΩω+...))) |
| - |
φ(1ω13) = φ(1ωφ(1ωφ(1ω...2)2)2) |
ψ(ΩΩω+Ω2) = ψ(ΩΩω+Ω+ψ(ΩΩω+Ω+ψ(ΩΩω+Ω+...))) |
| - |
φ(2ω) = sup(φ(1ω1n)|n<ω) |
ψ(ΩΩω×2) = ψ(ΩΩω+Ωω) |
| - |
φ(3ω) = sup(φ(2ω1n)|n<ω) |
ψ(ΩΩω×3) |
| - |
φ(ωω) |
ψ(ΩΩω×ω) |
| - |
φ(1ω+1) = φ(φ(φ(...ω)ω)ω) |
ψ(ΩΩω+1) = ψ(ΩΩω×Ω) = ψ(ΩΩω×ψ(ΩΩω×ψ(ΩΩω×...))) |
| - |
φ(1ω+2) = φ(φ(φ(...ω+1)ω+1)ω+1) |
ψ(ΩΩω+2) = ψ(ΩΩω+1×Ω) = ψ(ΩΩω+1×ψ(ΩΩω+1×ψ(ΩΩω+1×...))) |
| - |
φ(1ω×2) |
ψ(ΩΩω×2) |
| - |
φ(1ω2) |
ψ(ΩΩω2) |
| - |
φ(1ωω) |
ψ(ΩΩωω) |
| - |
φ(1ε0) = φ(1φ(11)) |
ψ(ΩΩψ(Ω)) |
| - |
φ(1Г0) = φ(1φ(12)) |
ψ(ΩΩψ(ΩΩ)) |
| - |
φ(1φ(1,0,0,0)) = φ(1φ(13)) |
ψ(ΩΩψ(ΩΩ2)) |
| - |
φ(1φ(1ω)) = φ(1φ(1φ(10))) |
ψ(ΩΩψ(ΩΩω)) |
| - |
φ(1φ(1Г0)) = φ(1φ(1φ(12))) |
ψ(ΩΩψ(ΩΩψ(ΩΩ))) |
| - |
φ(1φ(1φ(1ω))) = φ(1φ(1φ(1φ(10)))) |
ψ(ΩΩψ(ΩΩψ(ΩΩω))) |
| - |
φ(1φ(1φ(1φ(1...)))) |
ψ(ΩΩΩ) = ψ(ΩΩψ(ΩΩψ(ΩΩ...))) |
таб.19 (Сравнение ординальных нотаций Кантора, Веблена и Бухольца)
Надеюсь вы пережили и хорошенько усвоили и этот блок сравнений. Выходя за пределы Большого ординала Веблена уровень рекурсий становится, столь мощный, что заново пройдя через весь круг рекурсий Функции Веблена, где Большой ординал Веблена это первая неподвижная точка α↦φ(1α), второй неподвижной точкой окажется лишь ψ(ΩΩΩ×2).
ψ(ΩΩΩ)×ω = ωψ(ΩΩΩ)+1 = φ(ψ(ΩΩΩ)+1) = ψ(ΩΩΩ+1)
ψ(ΩΩΩ)2 = ωψ(ΩΩΩ)×2 = φ(ψ(ΩΩΩ)×2) = ψ(ΩΩΩ+ψ(ΩΩΩ))
ψ(ΩΩΩ)ω = ωωψ(ΩΩΩ)+1 = φ(φ(ψ(ΩΩΩ)+1)) = ψ(ΩΩΩ+ψ(ΩΩΩ+1))
ψ(ΩΩΩ)ψ(ΩΩΩ) = ωωψ(ΩΩΩ)×2 = φ(φ(ψ(ΩΩΩ)×2)) = ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ)))
ψ(ΩΩΩ)ψ(ΩΩΩ)ω = ωωωψ(ΩΩΩ)+1 = φ(φ(φ(ψ(ΩΩΩ)+1))) = ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ+1)))
ψ(ΩΩΩ)ψ(ΩΩΩ)ψ(ΩΩΩ) = ωωωψ(ΩΩΩ)×2 = φ(φ(φ(ψ(ΩΩΩ)×2))) = ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ))))
φ(1,ψ(ΩΩΩ)+1) = εψ(ΩΩΩ)+1 = ψ(ΩΩΩ+Ω) = ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ+...))))
φ(2,ψ(ΩΩΩ)+1) = ζψ(ΩΩΩ)+1 = ψ(ΩΩΩ+Ω2)
φ(3,ψ(ΩΩΩ)+1) = ηψ(ΩΩΩ)+1 = ψ(ΩΩΩ+Ω3)
φ(1,0,ψ(ΩΩΩ)+1) = Гψ(ΩΩΩ)+1 = ψ(ΩΩΩ+ΩΩ)
φ(2,0,ψ(ΩΩΩ)+1) = Pψ(ΩΩΩ)+1 = ψ(ΩΩΩ+ΩΩ×2)
φ(3,0,ψ(ΩΩΩ)+1) = Bψ(ΩΩΩ)+1 = ψ(ΩΩΩ+ΩΩ×3)
φ(1,0,0,ψ(ΩΩΩ)+1) = ψ(ΩΩΩ+ΩΩ2)
φ(1,0,0,0,ψ(ΩΩΩ)+1) = ψ(ΩΩΩ+ΩΩ3)
φ(1ω,ψ(ΩΩΩ)+10) = ψ(ΩΩΩ+ΩΩω)
φ(1ε0,ψ(ΩΩΩ)+10) = ψ(ΩΩΩ+ΩΩψ(Ω))
φ(1Г0,ψ(ΩΩΩ)+10) = ψ(ΩΩΩ+ΩΩψ(ΩΩ))
φ(1φ(1φ(1ω)),ψ(ΩΩΩ)+10) = ψ(ΩΩΩ+ΩΩψ(ΩΩω))
φ(1ψ(ΩΩΩ)10) = φ(1φ(1φ(1φ(1...))),ψ(ΩΩΩ)+10) = ψ(ΩΩψ(ΩΩψ(ΩΩ...))) = ψ(ΩΩΩ+ΩΩψ(ΩΩΩ))
φ(1φ(1ωψ(ΩΩΩ)+10)) = ψ(ΩΩΩ+ΩΩψ(ΩΩΩ+ΩΩω))
φ(1φ(1ψ(ΩΩΩ)10)) = ψ(ΩΩΩ+ΩΩψ(ΩΩΩ+ΩΩψ(ΩΩΩ)))
φ(1φ(1φ(1ωψ(ΩΩΩ)+10))) = ψ(ΩΩΩ+ΩΩψ(ΩΩΩ+ΩΩψ(ΩΩΩ+ΩΩω)))
φ(1φ(1φ(1...φ(1ψ(ΩΩΩ)10)...))) = ψ(ΩΩΩ+ΩΩψ(ΩΩΩ+ΩΩψ(ΩΩΩ+ΩΩ...))) = ψ(ΩΩΩ+ΩΩΩ) = ψ(ΩΩΩ×2)
Ну а рекурсии Ординальной коллапсирующей функции Бухольца можно с легкостью продолжить дальше. Давайте рассмотрим основные диагонализации на пути от ψ(ΩΩΩ) к ψ(ΩΩΩΩ). В представленных ниже сравнениях можно заметить одну важную деталь, что в целом способ создаваемых рекурсий над ординалами при переходе от ψ(ΩΩΩ) к ψ(ΩΩΩΩ) сопоставим со способом создаваемых рекурсий над конечными числами с использованием Иерархии Харди при переходе от hωωω(n) к hωωωω(n), хотя сопоставление это очень условное, но все же позволяет прочувствовать принципы Иерархии Бахмана. Кстати где-то между рекурсивной способностью ординалов ψ(ΩΩΩ) и ψ(ΩΩΩΩ), найдется рекурсивный предел функции, с помощью которой Джонатану Бауэрсу, создателю изначальной массивной нотации, удалось создать свое самое большое число. Как я говорил, развитие его нотации шло несколько по иному пути, нежели мы сейчас с вами рассматриваем, и его последнее расширение массивной нотации называлось Легионная массивная нотация, для которой, как в своих работах показал Крис Бёрд[187], масштаб рекурсий уровня ψ(ΩΩΩ×ω) являлся пределом, хотя стоит отметить, что многие считают, что последние наработки Бауэрса уже не были вполне упорядоченной нотацией.
ψ(ΩΩΩ+1) = ψ(ΩΩΩ×Ω) = ψ(ΩΩΩ×ψ(ΩΩΩ×ψ(ΩΩΩ×...)))
ψ(ΩΩΩ+2) = ψ(ΩΩΩ+1×Ω) = ψ(ΩΩΩ+1×ψ(ΩΩΩ+1×ψ(ΩΩΩ+1×...)))
ψ(ΩΩΩ+Ω) = ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ+...)))
ψ(ΩΩΩ+Ω+1) = ψ(ΩΩΩ+Ω×Ω) = ψ(ΩΩΩ+Ω×ψ(ΩΩΩ+Ω×ψ(ΩΩΩ+Ω×...)))
ψ(ΩΩΩ+Ω+2) = ψ(ΩΩΩ+Ω+1×Ω) = ψ(ΩΩΩ+Ω+1×ψ(ΩΩΩ+Ω+1×ψ(ΩΩΩ+Ω+1×...)))
ψ(ΩΩΩ+Ω×2) = ψ(ΩΩΩ+Ω+Ω) = ψ(ΩΩΩ+Ω+ψ(ΩΩΩ+Ω+ψ(ΩΩΩ+Ω+...)))
ψ(ΩΩΩ+Ω2) = ψ(ΩΩΩ+Ω×Ω) = ψ(ΩΩΩ+Ω×ψ(ΩΩΩ+Ω×ψ(ΩΩΩ+Ω×...)))
ψ(ΩΩΩ+Ω3) = ψ(ΩΩΩ+Ω2×Ω) = ψ(ΩΩΩ+Ω2×ψ(ΩΩΩ+Ω2×ψ(ΩΩΩ+Ω2×...)))
ψ(ΩΩΩ×2) = ψ(ΩΩΩ+ΩΩ) = ψ(ΩΩΩ+Ωψ(ΩΩΩ+Ωψ(ΩΩΩ+...)))
ψ(ΩΩΩ×2+1) = ψ(ΩΩΩ×2×Ω) = ψ(ΩΩΩ×2×ψ(ΩΩΩ×2×ψ(ΩΩΩ×2×...)))
ψ(ΩΩΩ×2+Ω) = ψ(ΩΩΩ×2+ψ(ΩΩΩ×2+ψ(ΩΩΩ×2+...)))
ψ(ΩΩΩ×3) = ψ(ΩΩΩ×2+ΩΩ) = ψ(ΩΩΩ×2+Ωψ(ΩΩΩ×2+Ωψ(ΩΩΩ×2+...)))
ψ(ΩΩΩ+1) = ψ(ΩΩΩ×Ω) = ψ(ΩΩΩ×ψ(ΩΩΩ×ψ(ΩΩΩ×...)))
ψ(ΩΩΩ+1+1) = ψ(ΩΩΩ+1×Ω) = ψ(ΩΩΩ+1×ψ(ΩΩΩ+1×ψ(ΩΩΩ+1×...)))
ψ(ΩΩΩ+1+ΩΩ) = ψ(ΩΩΩ+1+Ωψ(ΩΩΩ+1+Ωψ(ΩΩΩ+1+...)))
ψ(ΩΩΩ+1×2) = ψ(ΩΩΩ+1+ΩΩ×Ω) = ψ(ΩΩΩ+ΩΩ×ψ(ΩΩΩ+ΩΩ×ψ(ΩΩΩ+ΩΩ×...)))
ψ(ΩΩΩ+2) = ψ(ΩΩΩ+1×Ω) = ψ(ΩΩΩ+1×ψ(ΩΩΩ+1×ψ(ΩΩΩ+1×...)))
ψ(ΩΩΩ×2) = ψ(ΩΩΩ+Ω) = ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ+...)))
ψ(ΩΩΩ×3) = ψ(ΩΩΩ×2+Ω) = ψ(ΩΩΩ×2+ψ(ΩΩΩ×2+ψ(ΩΩΩ×2+...)))
ψ(ΩΩΩ2) = ψ(ΩΩΩ×Ω) = ψ(ΩΩΩ×ψ(ΩΩΩ×ψ(ΩΩΩ+...)))
ψ(ΩΩΩ2+1) = ψ(ΩΩΩ2×Ω) = ψ(ΩΩΩ2×ψ(ΩΩΩ2×ψ(ΩΩΩ2×...)))
ψ(ΩΩΩ2+Ω) = ψ(ΩΩΩ2+ψ(ΩΩΩ2+ψ(ΩΩΩ2+...)))
ψ(ΩΩΩ2+ΩΩ) = ψ(ΩΩΩ2+Ωψ(ΩΩΩ2+Ωψ(ΩΩΩ2+...)))
ψ(ΩΩΩ2+ΩΩ+1) = ψ(ΩΩΩ2+ΩΩ×Ω) = ψ(ΩΩΩ2+ΩΩ×ψ(ΩΩΩ2+ΩΩ×ψ(ΩΩΩ2+ΩΩ×...)))
ψ(ΩΩΩ2+ΩΩ×2) = ψ(ΩΩΩ2+ΩΩ+Ω) = ψ(ΩΩΩ2+ΩΩ+ψ(ΩΩΩ2+ΩΩ+ψ(ΩΩΩ2+ΩΩ+...)))
ψ(ΩΩΩ2×2) = ψ(ΩΩΩ2+ΩΩ×Ω) = ψ(ΩΩΩ2+ΩΩ×ψ(ΩΩΩ2+ΩΩ×ψ(ΩΩΩ2+ΩΩ×...)))
ψ(ΩΩΩ2+1) = ψ(ΩΩΩ2×Ω) = ψ(ΩΩΩ2×ψ(ΩΩΩ2×ψ(ΩΩΩ2×...)))
ψ(ΩΩΩ2+Ω) = ψ(ΩΩΩ2+ψ(ΩΩΩ2+ψ(ΩΩΩ2+...)))
ψ(ΩΩΩ2+Ω×2) = ψ(ΩΩΩ2+Ω+Ω) = ψ(ΩΩΩ2+Ω+ψ(ΩΩΩ2+Ω+ψ(ΩΩΩ2+Ω+...)))
ψ(ΩΩΩ2×2) = ψ(ΩΩΩ2+Ω×Ω) = ψ(ΩΩΩ2+Ω×ψ(ΩΩΩ2+Ω×ψ(ΩΩΩ2+Ω×...)))
ψ(ΩΩΩ3) = ψ(ΩΩΩ2×Ω) = ψ(ΩΩΩ2×ψ(ΩΩΩ2×ψ(ΩΩΩ2×...)))
ψ(ΩΩΩΩ) = ψ(ΩΩΩψ(ΩΩΩψ(...)))
С такими рекурсиями матричный способ нумерации неподвижных точек уже не справится. Однако мы можем попробовать расширить матричный вид Функции Веблена, увеличивая количество уровней матричной записи, так и назовем наш метод Расширенной матричной Функцией Веблена. Не буду давать формальных определений этой функции, поскольку и фундаментальные последовательности для получения больших чисел на основе ординалов, описываемых этой функцией, и нормальную форму этих ординалов, и сам метод их рекурсивного построения пришлось бы прописывать отдельно для каждого расширения. В любом случае у нас уже есть намного более простая и более сильная формально определенная Ординальная коллапсирующая функция Бухольца, поэтому я просто в сравнении с ней покажу как бы работало это расширение Функции Веблена, чтобы вы еще раз убедились, насколько Иерархия Веблена своей доступностью и наглядностью проигрывает Иерархии Бахмана. Скажу только, что все принципы матричной записи в расширенной функции будут сохранены, и если в вертикальном столбце матрицы первый стоит ноль, то такой столбец можно не писать, так же можно не записывать незначащие нули внизу столбцов.
φ(101) = φ(1010) = 1.н.т. α↦φ(1α) = φ(1φ(1φ(1φ(1...)))) = ψ(ΩΩΩ)
φ(101100) = φ(1011) = 2.н.т. α↦φ(1α) = φ(1φ(1φ(1...φ(1φ(101)10)...))) = ψ(ΩΩΩ×2)
φ(101200) = φ(1012) = 3.н.т. α↦φ(1α) = φ(1φ(1φ(1...φ(1φ(101100)10)...))) = ψ(ΩΩΩ×3)
φ(101110) = φ(1011,0) = 1.н.т. α↦φ(101α00) = 1.н.т. α↦φ(101α) = ψ(ΩΩΩ×Ω) = ψ(ΩΩΩ+1)
φ(101110100) = φ(1011,1) = 2.н.т. α↦φ(101α00) = 2.н.т. α↦φ(101α) = ψ(ΩΩΩ+1×2)
φ(101210) = φ(1012,0) = 1.н.т. α↦φ(101110α00) = 2.н.т. α↦φ(1011,α) = ψ(ΩΩΩ+1×Ω) = ψ(ΩΩΩ+2)
φ(101120) = φ(1011,0,0) = 1.н.т. α↦φ(101α10) = 1.н.т. α↦φ(101α,0) = ψ(ΩΩΩ+Ω)
φ(101120100) = φ(1011,0,1) = 2.н.т. α↦φ(101α10) = 2.н.т. α↦φ(101α,0) = ψ(ΩΩΩ+Ω×2)
φ(101120110) = φ(1011,1,0) = 1.н.т. α↦φ(101120α00) = 1.н.т. α↦φ(1011,0,α) = ψ(ΩΩΩ+Ω×Ω) = ψ(ΩΩΩ+Ω+1)
φ(101120210) = φ(1011,2,0) = α↦φ(101120110α00) = 1.н.т. α↦φ(1011,1,α) = ψ(ΩΩΩ+Ω+1×Ω) = ψ(ΩΩΩ+Ω+2)
φ(101220) = φ(1012,0,0) = 1.н.т. α↦φ(101120α10) = 1.н.т. α↦φ(1011,α,0) = ψ(ΩΩΩ+Ω+Ω) = ψ(ΩΩΩ+Ω×2)
φ(101130) = φ(1011,0,0,0) = 1.н.т. α↦φ(101α20) = 1.н.т. α↦φ(101α,0,0) = ψ(ΩΩΩ+Ω×Ω) = ψ(ΩΩΩ+Ω2)
φ(101140) = φ(1011,0,0,0,0) = 1.н.т. α↦φ(101α30) = 1.н.т. α↦φ(101α,0,0,0) = ψ(ΩΩΩ+Ω2×Ω) = ψ(ΩΩΩ+Ω3)
φ(1011ω0) = sup(φ(1011n0)|n<ω) = φ(1011,0,0,0,...) = ψ(ΩΩΩ+Ωω)
φ(201) = 1.н.т. α↦φ(1011α0) = ψ(ΩΩΩ+ΩΩ) = ψ(ΩΩΩ×2)
φ(201100) = 2.н.т. α↦φ(1011α0) = ψ(ΩΩΩ×2×2)
φ(201110) = 1.н.т. α↦φ(201α00) = ψ(ΩΩΩ×2×Ω) = ψ(ΩΩΩ×2+1)
φ(201120) = 1.н.т. α↦φ(201α10) = ψ(ΩΩΩ×2+Ω)
φ(301) = 1.н.т. α↦φ(2011α0) = ψ(ΩΩΩ×2+ΩΩ) = ψ(ΩΩΩ×3)
φ(ω01) = sup(φ(n01)|n<ω) = ψ(ΩΩΩ×ω)
φ(111) = 1.н.т. α↦φ(α01) = ψ(ΩΩΩ×Ω) = ψ(ΩΩΩ+1)
φ(111100) = 2.н.т. α↦φ(α01) = ψ(ΩΩΩ+1×2)
φ(111110) = 1.н.т. α↦φ(111α00) = ψ(ΩΩΩ+1×2)
φ(111101) = 1.н.т. α↦φ(1111α0) = ψ(ΩΩΩ+1×Ω) = ψ(ΩΩΩ+1+1)
φ(111201) = 1.н.т. α↦φ(1111011α0) = ψ(ΩΩΩ+1+ΩΩ)
φ(111301) = 1.н.т. α↦φ(1112011α0) = ψ(ΩΩΩ+1+ΩΩ×2)
φ(211) = 1.н.т. α↦φ(111α01) = ψ(ΩΩΩ+1×2)
φ(121) = 1.н.т. α↦φ(α11) = ψ(ΩΩΩ+1×Ω) = ψ(ΩΩΩ+2)
φ(102) = 1.н.т. α↦φ(1α1) = ψ(ΩΩΩ+Ω) = ψ(ΩΩΩ×2)
φ(103) = 1.н.т. α↦φ(1α2) = ψ(ΩΩΩ×3) = ψ(ΩΩΩ×2+Ω)
φ(1001) = 1.н.т. α↦φ(10α) = ψ(ΩΩΩ×Ω) = ψ(ΩΩΩ2)
φ(10011000) = φ(1001100) = φ(100110) = φ(10011) = 2.н.т. α↦φ(10α) = ψ(ΩΩΩ2×2)
φ(10011100) = φ(1001110) = φ(100111) = φ(10011,0) = 1.н.т. α↦φ(1001α000) = ψ(ΩΩΩ2×Ω) = ψ(ΩΩΩ2+1)
φ(10011200) = φ(1001120) = φ(100112) = φ(10011,0,0) = 1.н.т. α↦φ(1001α000) = ψ(ΩΩΩ2+Ω)
φ(10011ω00) = φ(10011ω0) = φ(10011ω) = φ(10011,0,0,0,...) = ψ(ΩΩΩ2+Ωω)
φ(10011010) = φ(1001101) = 1.н.т. α↦φ(10011α00) = ψ(ΩΩΩ2+ΩΩ)
φ(10011110) = φ(1001111) = 1.н.т. α↦φ(1001α010) = ψ(ΩΩΩ2+ΩΩ+1)
φ(10011020) = φ(1001102) = 1.н.т. α↦φ(10011α10) = ψ(ΩΩΩ2+ΩΩ×2)
φ(2001) = 1.н.т. α↦φ(100110α0) = ψ(ΩΩΩ2+ΩΩ2) = ψ(ΩΩΩ2×2)
φ(1101) = 1.н.т. α↦φ(α001) = ψ(ΩΩΩ2×Ω) = ψ(ΩΩΩ2+1)
φ(1011) = 1.н.т. α↦φ(1α01) = ψ(ΩΩΩ2+Ω)
φ(1021) = 1.н.т. α↦φ(1α21) = ψ(ΩΩΩ2+Ω×2)
φ(1002) = 1.н.т. α↦φ(10α1) = ψ(ΩΩΩ2×2) = ψ(ΩΩΩ2+Ω×Ω)
φ(10001) = 1.н.т. α↦φ(100α) = ψ(ΩΩΩ2×Ω) = ψ(ΩΩΩ3)
φ(100...1) = ψ(ΩΩΩω)
Получается, что пределом Расширенной матричной Функции Веблена будет лишь ординал ψ(ΩΩΩω). Ну что же, не очень то далеко нам удалось продвинуться. Мы даже не дотянули до ψ(ΩΩΩΩ), и чтобы добраться до него нам придется придумать какой-то способ, чтобы записывать высоту матрицы, так же как мы записывали длину, указывая лишь номера значащих позиций. Тогда мы сможем записать трансфинитные значения высоты матрицы и в этом случае при помощи трансфинитной рекурсии сможем добраться до ψ(ΩΩΩΩ), но такой способ записи будет невроятно громоздким. В ординальной коллапсирующей функции, как видите, все проще и нагляднее, нам достаточно городить степенные башни из Ω и вложенности функций ψ(n).
Собственно, увеличивая уровень степенной башни из несчетного ординала внутри коллапсирующей функции и, используя для записи тетрацию, мы доберемся, минуя ε0 = ψ(Ω) = ψ(1Ω), Г0 = ψ(ΩΩ) = ψ(2Ω), ψ(ΩΩΩ) = ψ(3Ω), ψ(ΩΩΩΩ) = ψ(4Ω), ψ(ΩΩΩΩΩ) = ψ(5Ω), ..., до ψ(ΩΩΩΩ...) = ψ(ωΩ). Это значимый ординал, у которого есть свое имя: Ординал Бахмана-Говарда (Bachmann-Howard ordinal)[188], он является предельным ординалом для многих аксиоматических систем[189]. Чтобы не быть голословным, приведу пример хотя бы одной. Для этого давайте определим еще одну подсистему арифметики второго порядка. Так же как в подсистеме арифметической трансфинитной рекурсии (ATR0) аксиома индукции в ней будет распространяться на бесконечные множества натуральных чисел, но это будет индукция несколько иной природы нежели мы с вами привыкли (стандартная индукция первого порядка, гласит что утверждение верное для n и для n+1, верно для всех натуральных чисел, или ординалов в случае с ATR0). Индукция, которую мы с вами определим, называется ограничивающей индукцией (bar induction). В двух словах аксиома ограничивающей индукции утверждает, что то, что верно для бесконечной последовательности натуральных чисел, должно быть верно и для конечного участка этой последовательности. Вроде бы очевидное утверждение, но все же оно недоказуемо и может быть определено только аксиоматически[190]. Интересно то, что изменив индукцию таким образом, мы можем создавать из множеств натуральных чисел намного более сильные рекурсии, чем в подсистеме ATR0. А сама подсистема арифметики второго порядка, включающая такое изменение, будет называться Аксиомами арифметического свертывания с ограничивающей индукцией, по-английски: Arithmetical comprehension axioms with Bar induction (ACA+BI). А как я и говорил, PTO ACA+BI = ψ(ωΩ)[191].
Ну а поскольку Ординал Бахмана-Говарда ψ(ωΩ) является пределом для большинства теорий, то как следствие, на нем так же сходится и большинство рекурсивных систем. Например, все другие способы усиления Функции Веблена обречены столкнуться с этим пределом, если конечно смогут до него добраться. Мы могли бы взять расширенную матричную Функцию Веблена, которая работает с полноценными двухмерными матрицами любого размера и еще расширить ее, чтобы она могла работать с трехмерными матрицами. Как раз в третье измерение отмечалась бы высота матрицы и туда бы расширялись все рекурсии накрученные на неподвижных точках этой высоты, тогда пределом трехмерных матриц стал бы ординал ψ(ΩΩΩΩω). Если бы мы расширили матрицы так чтобы они могли уходить в четвертое измерение, то пределом четырехмерных матриц стал бы ординал ψ(ΩΩΩΩΩω), но в этом случае нормальная форма Функции Веблена не просто стала бы сложна в восприятии, а более того ее наглядность физически бы стала невозможна (хотя тут многие программисты упрекнули бы меня, сказав что для наглядности мы могли бы использовать метод многомерных массивов, который используется во многих языках программирования). В общем получается, что ординал ψ(ωΩ) был бы сопоставим с бесконечномерными матрицами Функции Веблена. Тут можно отметить некую схожесть, ведь как предел Расширенной нотации Кантора с бесконечным количеством измерений индексов был сопоставим с пределом линейной иерархии Веблена, так же предел многомерной иерархии Веблена с бесконечным количеством измерений будет сопоставим с пределом иерархии Бахмана. Но хочу отметить, что хоть ординал ψ(ωΩ) и является пределом иерархии Бахмана, он еще не является пределом ординальной коллапсирующей функции Бухольца, ее дальнейшие рекурсивные возможности столь сильны, что даже если мы придумаем матрицы с трансфинтино-ординальными измерениями, они все равно не идут с ними ни в какое сравнение, но об этом мы поговорим в следующей части.
Следующее расширение массивной нотации, по уровню рекурсий тоже не сможет преодолеть предел иерархии Бахмана ψ(ωΩ), поэтому пока тех знаний об ординальной коллапсирующей функции, которые я вам дал, нам хватит чтобы полностью его измерить и понять масштабы создаваемых рекурсий. Мы очень долго говорили об ординалах и вы могли подзабыть принципы предыдущего расширения, поэтому перед тем как идти дальше вернитесь и еще раз перечитайте все что связано с Примитивно расширяющейся массивной нотацией, потому что следующее расширение начинается, простите за тавтологию, с расширения этих принципов.
В Примитивно расширяющейся массивной нотации мы ввели понятие разделителей разного порядка, где первый порядок:
, = (1) = (1.0)
(2) = (2.0)
(1,2) = (1(1.0)2.0)
(1(2)2) = (1(2.0)2.0)
и т.д.;
второй порядок:
. = (1.) = (1.1)
(2.) = (2.1)
(1,2.) = (1(1.0)2.1)
(1(2.)2.) = (1(2.1)2.1)
и т.д.;
n-ный порядок:
(1.n-1)
(2.n-1)
(1,2.n-1)
(1(2.n-1)2.n-1)
Так же я отметил, что можно было бы расширить эту концепцию, сделав диагонализацию при помощи введения вхождений и разделителей уже в самом порядке, однако такое расширение было бы очень слабым. Английский математик Крис Бёрд придумал иную, более сильную рекурсию, которую он назвал иерархией разделителей[167]. Прежде всего вводится " ' " - который называют разделителем первичного разделения, среди всех известных нам разделителей он имеет наивысший уровень и расширять разделители надо начинать именно с него, переходя к разделителям более низких уровней. Эта иерархическая особенность разделителя первичного разделения отражена в формальном определении функции внутри измененного процесса исключений, там детально расписана процедура расширения. Расширение массива заканчивается когда все разделители будут иметь минимальный уровень (1'1) = "," - после чего мы перейдем к правилам обычной массивной нотации. Я не буду детально расписывать как работает тот пункт процесса исключений, по которому происходит расширение, ибо это достаточно сложный рекурсивный алгоритм, просто давайте посмотрим какую иерархию уровней разделителей можно создать при помощи первичного расширения. Первый порядок в записи первичного расширения будет выглядеть так:
, = (1) = (1.0) = (1'1)
(2) = (2.0) = (2'1)
(1,2) = (1,2.0) = (1,2'1)
(1(2)2) = (1(2.0)2.0) = (1(2'1)2'1)
Однако разделители первого порядка не принято записывать в виде первичного расширения, все равно в этом случае расширение сводится к правилам обычной Расширенной массивной нотации, поэтому употребляемой будет запись без указания порядка. А вот разделители второго порядка уже необходимо записывать по правилам первичного расширения:
. = (1.) = (1.1) = (1'2)
(2.) = (2.1) = (2'2)
(1,2.) = (1,2.1) = (1,2'2)
(1(2.)2.) = (1(2.1)2.1) = (1(2'2)2'2)
Ну и соответственно n-ный порядок разделения будет выглядеть так:
(1.n-1) = (1'n)
(2.n-1) = (2'n)
(1,2.n-1) = (1,2'n)
(1(2.n-1)2.n-1) = (1(2'n)2'n)
Хотя разделитель (1'n) записывается уже так (1'1,2) и это равносильно тому, как если бы мы оставили схему примитивного расширения и внедрили вхождения и разделители для диагонализации порядка (1.1,2). Следующий разделитель это (2'1,2) и чтобы поэтапно расписать как до него добраться от (1'1,2) нужно снова разобрать круг рекурсий, который заложен в основе массивной нотации, и который должен пройти каждый разделитель (с учетом своего масштаба рекурсий). И если {n,n(1'n)2} = {n,n(1'1,2)2}, то {n,n,2(1'1,2)2} = {n,n(1'{n,n(1'...{n,n(1'1,2)2}...)2})2} - где n-1 вложений. Затем {n,n,1,2(1'1,2)2} = {n,n,2(1'1,2)2}, потом {n,n(2)2(1'1,2)2} = {n,n,n,n,n,...(1'1,2)2}, далее {n,n(1'1,2)3} = {n,n(1'n)2(1'1,2)2}, следом {n,n(1'1,2)1,2} = {n,n(1'1,2)n}, и еще {n,n(1'1,2)1(1'1,2)2} = {n,n(1'1,2)1(1'n)2}, ну и наконец {n,n(2'1,2)2} = {n,n(1'1,2)1(1'1,2)1(1'1,2)1(1'1,2)...2}.
И такой путь преобразований проходит каждый разделитель, чтобы стать "следующим" разделителем. Можете еще раз в этом убедиться, посмотрев предыдущие сравнения. Понятно, что всякий раз подобные преобразования являют собой рекурсии все бо́льших масштабов, но принцип остается тем же. Ну а поскольку абсолютно любой новый разделитель, появляющийся в расширенных версиях массивной нотации, при увеличении рекурсий проходит одинаковый путь внутри массива, конечно с учетом все возрастающего масштаба рекурсий, то больше нет смысла разбирать одни и те же преобразования. Поэтому впредь такие преобразования я больше не буду демонстрировать, потому что если всякий раз повторно разбирать уже пройденные методы создания рекурсий, мы так и не сдвинемся с места. Отмечу только, что эта наследственная особенность продиктована базовыми правилами линейной массивной нотации, предел которых достигался рекурсиями уровня fωω(n). Когда были введены разделители разных уровней приемственность этого принципа сохранилась. Поэтому соответствующий уровень рекурсий, на котором появляется "следующий" разделитель в сравнении с рекурсивными преобразованиями ординалов в функциях быстрорастущей иерархии всегда будет соответствовать fωωα(n) > {n,n(...)2}. Например: fωω1(n) = fωω(n) > {n,n(2)2} = {n,n(2'1)2} и fωω2(n) > {n,n(3)2} = {n,n(3'1)2}, и так далее. С введением разделителей разного порядка эта преемственность так же сохраняется: fωωε0(n) = fε0(n) > {n,n(1'2)2}, fωωε0+1(n) > {n,n(2'2)2}, fωωε0+2(n) > {n,n(3'2)2}, и fωωε1(n) = fε1(n) > {n,n(1'3)2}, fωωε1+1(n) > {n,n(2'3)2}, fωωε1+2(n) > {n,n(3'3)2}. Можно заметить, что всякая новая неподвижная точка функции α↦ωα приводит к смене порядка разделителя, и поскольку из ее свойств вытекает что ωωα = α, то тогда мы имеем сравнение fα(n) > {n,n(...)2}. После чего "следующий" уровень разделителя появляется только когда fωωα+1(n) = fαω(n) > {n,n(2...)2}. Чтобы еще раз хорошо усвоить, то что я здесь объяснил, взгляните снова на перечень сравнений примитивно расширяющейся массивной нотации, где наглядно показано как эта особенность сравнений себя проявляет. Думаю больше возвращаться к объяснению этого нам не придется.
Давайте лучше будем наращивать рекурсии в разделителях. Хотя и там все происходит похожим образом. Разделитель (n'1,2) как всегда соответствует диагонализации (1,2'1,2), а рекурсивно увеличивая его, мы можем добраться до (1(1'1,2)2'1,2). Далее так же (n(1'1,2)2'1,2) = (1,2(1'1,2)2'1,2), и (1(1'n)2(1'1,2)2'1,2) = (1,2(1'1,2)3'1,2). После чего рекурсии на (1(1'1,2)n'1,2) в итоге дадут нам выражение (1(1'1,2)1(1'1,2)2'1,2) и так до тех пор пока (1(1'1,2)1(1'1,2)1(1'1,2)...n раз...2'1,2) = (1(2'1,2)2'1,2). Затем рекурсии с (1(n'1,2)2'1,2) приведут к разделителю (1(1(1'1,2)2'1,2)2'1,2) и так далее, до тех пор пока (1'2,2) = (1(1(1(1... , ...2'1,2)2'1,2)2'1,2)2'1,2) - где n-1 вложений. Если бы мы придерживались схемы примитивного расширения с диагонализацией порядка, тогда (1'2,2) соответствовал бы (1.2,2).
Дальше начинаем наращивать рекурсии по другую сторону от " ' " - разделителя первичного разделения, пока рекурсивно не дойдем до уровня (1'1(1'1,2)2) = (1.1(1.1,2)2), после чего рекурсии на (1'1(1'1,n)2) в итоге дадут (1'1(1'1(1'1,2)2)2) = (1.1(1.1(1.1,2)2)2), и так далее до уровня (1'1'2) = (1'1(1'1(1'1(1'1... , ...2)2)2)2) - где n-1 вложений, что было бы равносильно (1.1.1) в примитивном расширении диагонализации порядка над порядком. Опустив подробности, сразу перейдем к (1'1'1'2), что соответствовало бы диагонализации порядка над порядком над порядком (1.1.1.1), затем к (1'1'1'1'2) = (1.1.1.1.1) и так далее к (1'1'1'1'...n раз...2) = (1(2')2). На этом моменте схема диагонализации порядков в примитивном расширении полностью исчерпала бы себя.
Но давайте разберемся, а что же (2') это такое? На самом деле, все просто, мы ввели разделитель первичного расширения второго уровня. Да, у них тоже могут быть уровни, а почему бы и нет, тогда " ' " = (1'). Это может быть плохо видно в типографском шрифте, но в такой записи апостроф ставится чуть выше чем обычно. Все разделители первичного расширения следующих после первого уровней работают по той же схеме что и обычные разделители, так что не только (1(2')2) = (1'1'1'1'...n раз...2), но и (1(3')2) = (1(2')1(2')1(2')1(2')...n раз...2), и (1(1,2')2) = (1(n')2), и так далее. Все подобные преобразования будут продолжаться до тех пор пока не станут одной гигантской чередой разделителей первичного расширения первого уровня " ' " = (1'). Первичное расширение в данном случае работает по тому же принципу: если в неком разделителе есть только вхождения равные единицам отделенным разделителями первичного расширения любого уровня (пусть это будет строка #1), а потом встречается " '2 ", после чего могут следовать любые другие вхождения с обычными или первичными разделителями (пусть это будет строка #2), и нигде не применимо правило сокращения, тогда расширение происходит следующим образом: (#1 '2 #2) = (#1(#1(#1(#1 ...,... 2 #2)2 #2)2 #2)2 #2). Если же после первичного разделителя встречается тройка " '3 ", то тогда расширение будет выглядеть так: (#1 '3 #2) = (#1(#1(#1(#1 ...,... 2'2 #2)2'2 #2)2'2 #2)2'2 #2) и так далее.
И теперь мы сможем наращивать уже этот уровень первичного расширения, начиная от (1(n')2) = (1(1,2')2) = (1(1(1(1')1)2')2), до (1(1(1(1(1(1... , ...2)2)2)2)2')2) = (1(1(1'2)2')2) = (1(1(1(1')2)2')2), и далее к (1(1(1'1'1'1'...2)2')2) = (1(1(1(2')2)2')2). После чего вновь от (1(1(1(n')2)2')2) = (1(1(1(1,2')2)2')2) = (1(1(1(1(1(1')1)2')2)2')2), до (1(1(1(1(1(1(1(1... , ...2)2)2)2)2')2)2')2) = (1(1(1(1(1'2)2')2)2')2) = (1(1(1(1(1(1')2)2')2)2')2), и далее снова переходя к (1(1(1(1(1'1'1'1'...2)2')2)2')2) = (1(1(1(1(1(2')2)2')2)2')2). И вновь продолжая (1(1(1(1(1(n')2)2')2)2')2) = (1(1(1(1(1(1,2')2)2')2)2')2) и так далее, вплоть до (1(1(1(1(1(1... , ...2')2)2')2)2')2) - где n-1 вложений. Что будет соответствовать уровню рекурсий быстрорастущей иерархии от Г0 - ординала Фефермана-Шутте.
Такая система вложений уровней разделителей первичного расширения тоже может быть диагонализирована разделителем (1'2'), давайте рассмотрим его подробнее. Можно сказать что на этом этапе у нас появился разделитель первичного расширения внутри разделителя первичного расширения, и он будет расширять уже уровни внешнего разделителя первичного расширения. Получается что мы вновь пришли к схеме диагонализации уровней разделителей над уровнями разделителей, но первичное расширение, в отличие от диагонализации порядков примитивного расширения, в такой схеме проявит очень мощные рекурсинвые способности, которые детально можно будет посмотреть в сравнительном анализе. Общий принцип расширения таков, что первичный разделитель " ' ", находясь внутри других первичных разделителей, которые он диагонализирует, при расширении должен захватывать все слои являющиеся первичными разделителями и один верхний слой не являющийся первичным разделителем. Так например: (1(1'2')2) = (1(1(1(1(1(1... , ...2')2)2')2)2')2), а (1(1(1'2')2')2) = (1(1(1(1(1(1(1(1(1... , ...2')2')2)2')2')2)2')2')2). В итоге рекурсии создаваемые диагонализацией уровня над уровнем первичного расширения приведут нас к системе вложенных выражений, начиная от (1(1'2')2) и далее к (1(1(1'2')2')2), затем к (1(1(1(1'2')2')2')2) и так далее, вплоть до (1(1(1(1(1(1... , ...2')2')2')2')2')2) - где n-1 вложений. Это будет предел Первично расширяющейся массивной нотации сопоставимый с рекурсиями ψ(ωΩ) - ординала Бахмана-Говарда. Теперь, я думаю, понятно почему было принято решение отказаться от примитивной вложенной иерархии порядков разделителей в пользу первичного расширения, с помощью которого создаваемая вложенная иерархия уровней будет намного сильнее. Ниже, я как всегда, привожу формальное определение нотации и сравнительные примеры, в которых по-прежнему буду использовать знак "~~", обозначающий сопоставление скорости роста выражения нотации со скоростью роста функции быстрорастущей иерархии взятой от некого ординала α, так чтобы она превышала скорость роста выражения нотации, но не превышала взятая от любого ординала меньшего α. Ну а в качестве ординальной нотации буду использовать ту, запись ординала α, в которой короче и нагляднее.
Первично расширяющаяся масcивная нотация (Primary expanding array notation)
Определение:
Действительны все определения Primitive expanding array notation
Действителен алгоритм сравнения уровней Extended array notation.
“ ' ” - апостроф (символ ASCII=39) разделитель первичного расширения.
(1'1) - это “(1.0)” - “,” - запятая, его краткая запись.
(1'2) - это “(1.1)” - “.” - точка, его краткая запись.
(1'3) - это “(1.2)”
(1'k) - это “(1.k-1)”
Расширение происходит следующим образом:
когда после “ ' ” встречается вхождение не равное 1, то
(1'…1'1'n #) изменяется на
Sb, где b - итератор,
S1 - “,” - запятая, и
Si+1 = (1'…1'1 Si 2'n-1 #).
“ ' ” - сам по себе лишь краткая запись (1
')
Следовательно (2
') разделитель первичного расширения следующего уровня.
Разделители первичного расширения разных уровней так же могут иметь вхождения,
например (2
'), (3
'), (1,2
'), (1(1,2)2
'), (1(1
')2
') и т.д.
При сравнении уровня первичные разделители “ (...
') ” всегда имееют бо́льший уровень, чем обычные “ (...) ”.
Уровни разделителей с разным количеством слоев создаваемые первичным расширением не образуют систему ординалов, потому что представляют собой бесконечно нисходящую цепь:
lv(') > lv((1'2)) > lv((1(1'2)2)) > lv((1(1(1'2)2)2)) >…
Правила:
Правило 1: (Правило базы - если в массиве два вхождения) {a S b} = {a,b} = a
b
Правило 2: (Правило хвоста - если последнее вхождение массива или разделителя равно 1)
{# S 1} = {#} или
(# S 1) = (#)
Правило 3: (Правило рекурсии - если 2-е и 3-е вхождение не равно 1)
{a,b,c #} = {a,{a,b-1,c #},c-1 #}
Правило 4: (Правило сокращения - если lv(S) < lv(S
+), для массива или разделителя) {# S 1 S
+ #
+} = {# S
+ #
+} или (# S 1 S
+ #
+) = (# B #
+)
“#” и “#+” - какие-то строки вхождений и разделителей, также могут быть пустыми.
“S” и “S+” - разделители.
Процесс:
Циклично и последовательно проверяем выполнение 4-х приведенных выше правил, пока не выполнится первое правило.
Если ни одно из 4-х приведенных выше правил не применяется, то запускается процесс исключений.
Начинаем с 3-ого вхождения:
Случай A: Если вхождение равно 1, тогда переходим к следующему вхождению.
Случай B: Если вхождение не равно 1, тогда смотрим на предыдущий элемент:
Случай B1: Если это запятая “,” тогда:
1) изменяем
“1,n” (это вхождение и предыдущую единицу) на
“b,n-1”, где b - итератор. *
2) изменяем все предыдущие вхождения в базовом слое на
a, где a - база. *
3) закончить и перейти к проверке правил.
Случай B2: Если это апостроф “ ' ” или “(1
')” что тоже самое, тогда:
1) пусть t это слой, на котором находится “ ' ”.
2) повторяем:
а. вычесть 1 из t.
b. пусть разделитель B
t находится в слое t и в нем находится “ ' ”.
с. если t = 1, то переходим к следующему пункту иначе повторяем этот пункт, начиная с подпункта a.
3) находим максимальный t, чтобы разделитель A
t не имел “ ' ” вверху сразу перед закрывающейся скобкой “)”.
4) пусть строки P и Q будут такими, что
Bt = “P ' n Q”
5) изменяем B
t на
Sb, где b - итератор,
S1 - “,” - запятая, и
Si+1 = “P Si 2 ' n-1 Q” *
6) закончить и перейти к проверке правил.
Случай B3: Если это разделитель “K”, не являющийся запятой или апострофом, тогда
1) изменяем
“K n” на “K 2 K n-1”. *
2) пусть разделитель
At = K, где K находится на слое t.
3) переходим к первому вхождению в первом из K.
Случай B4: Если это открывающаяся скобка “(” тогда:
1) изменяем разделитель “
(n #)” на строку
Sb, где b это итератор,
S1 = “(n-1 #)” и
Si+1 = “Si 1 (n-1 #)”. *
2) закончить и перейти к проверке правил.
Пункты, отмеченные звездочкой *, означают изменения в массиве.
Первоначальное авторство: Крис Бёрд, 2014 год
[167][192][193].
Последующая модификация: Hypcos, 2015 год.
[168]
приложение 16 (Первично расширяющаяся массивная нотация)
ε0 = φ(1,0) = ψ(Ω) ~~ {n,n(1'2)2} = {n,n(1(1(1(1... , ...2)2)2)2)2} n-1 вложений
ε0+1 ~~ {n,n,2(1'2)2} = {n,{n,...{n,n(1'2)2}...(1'2)2}(1'2)2} n-1 вложений
ε0+2 ~~ {n,n,3(1'2)2} = {n,{n,...{n,n(1'2)2}...,2(1'2)2},2(1'2)2} n-1 вложений
ε0+ω ~~ {n,n,1,2(1'2)2} = {n,n,n(1'2)2}
ε0×2 ~~ {n,n(1'2)3} = {n,n(1(1(1(1... , ...2)2)2)2)2(1'2)2} n-1 вложений
ε0×3 ~~ {n,n(1'2)4} = {n,n(1(1(1(1... , ...2)2)2)2)2(1'2)3} n-1 вложений
ωε0+1 ~~ {n,n(1'2)1,2} = {n,n(1'2)n}
ωε0×2 ~~ {n,n(1'2)1(1'2)2} = {n,n(1'2)1(1(1(1(1... , ...2)2)2)2)2} n-1 вложений
ωωε0+1 ~~ {n,n(2'2)2} = {n,n(1'2)1(1'2)1(1'2)...n-1 раз...2}
ωωε0+2 ~~ {n,n(3'2)2} = {n,n(2'2)1(2'2)1(2'2)...n-1 раз...2}
ωωε0+ω ~~ {n,n(1,2'2)2} = {n,n(n'2)2}
ωωε0×2 ~~ {n,n(1(1'2)2'2)2} = {n,n(1(1(1(1... , ...2)2)2)2'2)2} n-1 вложений
ωωε0×3 ~~ {n,n(1(1'2)3'2)2} = {n,n(1(1(1(1... , ...2)2)2)2(1'2)2'2)2} n-1 вложений
ωωωε0+1 ~~ {n,n(1(1'2)1,2'2)2} = {n,n(1(1'2)n'2)2}
ωωωε0×2 ~~ {n,n(1(1'2)1(1'2)2'2)2} = {n,n(1(1'2)1(1(1(1... , ...2)2)2)2'2)2} n-1 вложений
ωωωωε0+1 ~~ {n,n(1(2'2)2'2)2} = {n,n(1(1'2)1(1'2)1(1'2)...n раз...2'2)2}
ωωωωε0×2 ~~ {n,n(1(1(1'2)2'2)2'2)2} = {n,n(1(1(1(1(1... , ...2)2)2)2'2)2'2)2} n-1 вложений
ωωωωωε0+1 ~~ {n,n(1(1(1'2)1,2'2)2'2)2} = {n,n(1(1(1'2)n'2)2'2)2}
ωωωωωε0×2 ~~ {n,n(1(1(1'2)1(1'2)2'2)2'2)2} = {n,n(1(1(1'2)1(1(1(1... , ...2)2)2)2'2)2'2)2} n-1 вложений
ωωωωωωε0+1 ~~ {n,n(1(1(2'2)2'2)2'2)2} = {n,n(1(1(1'2)1(1'2)1(1'2)...n раз...2'2)2'2)2}
ωωωωωωε0×2 ~~ {n,n(1(1(1(1'2)2'2)2'2)2'2)2} = {n,n(1(1(1(1(1(1... , ...2)2)2)2'2)2'2)2'2)2} n-1 вложений
ε1 ~~ {n,n(1'3)2} = {n,n(1(1(1(1... , ...2'2)2'2)2'2)2'2)2} n-1 вложений
ε2 ~~ {n,n(1'4)2} = {n,n(1(1(1(1... , ...2'3)2'3)2'3)2'3)2} n-1 вложений
ε3 ~~ {n,n(1'5)2} = {n,n(1(1(1(1... , ...2'4)2'4)2'4)2'4)2} n-1 вложений
εω ~~ {n,n(1'1,2)2} = {n,n(1'n)2}
εω+1 ~~ {n,n,2(1'1,2)2} = {n,{n,...{n,n(1'1,2)2}...(1'1,2)2}(1'1,2)2} n-1 вложений
εω+ω ~~ {n,n,1,2(1'1,2)2} = {n,n,n(1'1,2)2}
εω+ωω ~~ {n,n(2)2(1'1,2)2} = {n,n,1,1,1,...n-1 раз...2(1'1,2)2}
εω+ε0 ~~ {n,n(1'2)2(1'1,2)2} = {n,n(1(1(1... , ...2)2)2)2(1'1,2)2} n-1 вложений
εω+ε1 ~~ {n,n(1'3)2(1'1,2)2} = {n,n(1(1(1... , ...2'2)2'2)2'2)2(1'1,2)2} n-1 вложений
εω×2 ~~ {n,n(1'1,2)3} = {n,n(1'n)2(1'1,2)2}
εω×2+1 ~~ {n,n,2(1'1,2)3} = {n,{n,...{n,n(1'1,2)3}...(1'1,2)3}(1'1,2)3} n-1 вложений
εω×2+ε0 ~~ {n,n(1'2)2(2'1,2)3} = {n,n(1(1(1... , ...2)2)2)2(2'1,2)3} n-1 вложений
εω×3 ~~ {n,n(1'1,2)4} = {n,n(1'n)2(1'1,2)3}
ωεω+1 ~~ {n,n(1'1,2)1,2} = {n,n(1'1,2)n}
ωεω+ω ~~ {n,n(1'1,2)1,1,2} = {n,n(1'1,2)n,n}
ωεω+ωω ~~ {n,n(1'1,2)1(2)2} = {n,n(1'1,2)1,1,1,...n раз...2}
ωεω+ε0 ~~ {n,n(1'1,2)1(1'2)2} = {n,n(1'1,2)1(1(1(1... , ...2)2)2)2} n-1 вложений
ωεω×2 ~~ {n,n(1'1,2)1(1'1,2)2} = {n,n(1'1,2)1(1'n)2}
ωωεω+1 ~~ {n,n(2'1,2)2} = {n,n(1'1,2)1(1'1,2)1(1'1,2)...n-1 раз...2}
ωωεω+ω ~~ {n,n(1,2'1,2)2} = {n,n(n'1,2)2}
ωωεω+ε0 ~~ {n,n(1(1'2)2'1,2)2} = {n,n(1(1(1(1... , ...2)2)2)2'1,2)2} n-1 вложений
ωωεω+ε1 ~~ {n,n(1(1'3)2'1,2)2} = {n,n(1(1(1(1... , ...2'2)2'2)2'2)2'1,2)2} n-1 вложений
ωωεω×2 ~~ {n,n(1(1'1,2)2'1,2)2} = {n,n(1(1'n)2'1,2)2}
ωωεω×2+1 ~~ {n,n(2(1'1,2)2'1,2)2} = {n,n(1(1'1,2)2'1,2)1(1(1'1,2)2'1,2)1(1(1'1,2)2'1,2)...n-1 раз...2}
ωωεω×2+ε0 ~~ {n,n(1(1'2)2(1'1,2)2'1,2)2} = {n,n(1(1(1(1... , ...2)2)2)2(1'1,2)2'1,2)2} n-1 вложений
ωωεω×3 ~~ {n,n(1(1'1,2)3'1,2)2} = {n,n(1(1'n)2(1'1,2)2'1,2)2}
ωωωεω+1 ~~ {n,n(1(1'1,2)1,2'1,2)2} = {n,n(1(1'1,2)n'1,2)2}
ωωωεω+ω ~~ {n,n(1(1'1,2)1,1,2'1,2)2} = {n,n(1(1'1,2)n,n'1,2)2}
ωωωεω+ωω ~~ {n,n(1(1'1,2)1(2)2'1,2)2} = {n,n(1(1'1,2)1,1,1,...n раз...2'1,2)2}
ωωωεω+ε0 ~~ {n,n(1(1'1,2)1(1'2)2'1,2)2} = {n,n(1(1'1,2)1(1(1(1... , ...2)2)2)2'1,2)2} n-1 вложений
ωωωεω×2 ~~ {n,n(1(1'1,2)1(1'1,2)2'1,2)2} = {n,n(1(1'1,2)1(1'n)2'1,2)2}
ωωωωεω+1 ~~ {n,n(1(2'1,2)2'1,2)2} = {n,n(1(1'1,2)1(1'1,2)1(1'1,2)...n раз...2'1,2)2}
ωωωωεω+ω ~~ {n,n(1(1,2'1,2)2'1,2)2} = {n,n(1(n'1,2)2'1,2)2}
ωωωωεω×2 ~~ {n,n(1(1(1'1,2)2'1,2)2'1,2)2} = {n,n(1(1(1'n)2'1,2)2'1,2)2}
ωωωωωεω+1 ~~ {n,n(1(1(1'1,2)1,2'1,2)2'1,2)2} = {n,n(1(1(1'1,2)n'1,2)2'1,2)2}
ωωωωωεω+ω ~~ {n,n(1(1(1'1,2)1,1,2'1,2)2'1,2)2} = {n,n(1(1(1'1,2)n,n'1,2)2'1,2)2}
ωωωωωεω×2 ~~ {n,n(1(1(1'1,2)1(1'1,2)2'1,2)2'1,2)2} = {n,n(1(1(1'1,2)1(1'n)2'1,2)2'1,2)2}
ωωωωωωεω+1 ~~ {n,n(1(1(2'1,2)2'1,2)2'1,2)2} = {n,n(1(1(1'1,2)1(1'1,2)1(1'1,2)...n раз...2'1,2)2'1,2)2}
ωωωωωωεω+ω ~~ {n,n(1(1(1,2'1,2)2'1,2)2'1,2)2} = {n,n(1(1(n'1,2)2'1,2)2'1,2)2}
ωωωωωωεω×2 ~~ {n,n(1(1(1(1'1,2)2'1,2)2'1,2)2'1,2)2} = {n,n(1(1(1(1'n)2'1,2)2'1,2)2'1,2)2}
εω+1 ~~ {n,n(1'2,2)2} = {n,n(1(1(1(1... , ...2'1,2)2'1,2)2'1,2)2'1,2)2} n-1 вложений
εω+2 ~~ {n,n(1'3,2)2} = {n,n(1(1(1(1... , ...2'2,2)2'2,2)2'2,2)2'2,2)2} n-1 вложений
εω×2 ~~ {n,n(1'1,3)2} = {n,n(1'n,2)2}
εω2 ~~ {n,n(1'1,1,2)2} = {n,n(1'n,n)2}
εωω ~~ {n,n(1'1(2)2)2} = {n,n(1'1,1,1,1,...n раз...2)2}
εωωω ~~ {n,n(1'1(1,2)2)2} = {n,n(1'1(n)2)2}
εωωωω ~~ {n,n(1'1(1(2)2)2)2} = {n,n(1'1(1,1,1,...n раз...2)2)2}
εωωωωω ~~ {n,n(1'1(1(1,2)2)2)2} = {n,n(1'1(1(n)2)2)2}
εε0 ~~ {n,n(1'1(1'2)2)2} = {n,n(1'1(1(1(1... , ...2)2)2)2)2} n-1 вложений
εε0+1 ~~ {n,n,2(1'1(1'2)2)2} = {n,{n,...{n,n(1'1(1'2)2)2}...(1'1(1'2)2)2}(1'1(1'2)2)2} n-1 вложений
εε0×2 ~~ {n,n(1'1(1'2)2)3} = {n,n(1'1(1(1(1... , ...2)2)2)2)2(1'1(1'2)2)2} n-1 вложений
ωεε0+1 ~~ {n,n(1'1(1'2)2)1,2} = {n,n(1'1(1'2)2)n}
ωεε0×2 ~~ {n,n(1'1(1'2)2)1(1'1(1'2)2)2} = {n,n(1'1(1'2)2)1(1'1(1(1(1... , ...2)2)2)2)2} n-1 вложений
ωωεε0+1 ~~ {n,n(2'1(1'2)2)2} = {n,n(1'1(1'2)2)1(1'1(1'2)2)1(1'1(1'2)2)...n-1 раз...2}
ωωεε0×2 ~~ {n,n(1(1'1(1'2)2)2'1(1'2)2)2} = {n,n(1(1'1(1(1(1... , ...2)2)2)2)2'1(1'2)2)2} n-1 вложений
εε0+1 ~~ {n,n(1'2(1'2)2)2} = {n,n(1(1(1... , ...2'1(1'2)2)2'1(1'2)2)2'1(1'2)2)2} n-1 вложений
εε0+ω ~~ {n,n(1'1,2(1'2)2)2} = {n,n(1'n(1'2)2)2}
εε0+ωω ~~ {n,n(1'1(2)2(1'2)2)2} = {n,n(1'1,1,1,1,...n раз...2(1'2)2)2}
εε0+ωωω ~~ {n,n(1'1(1,2)2(1'2)2)2} = {n,n(1'1(n)2(1'2)2)2}
εε0×2 ~~ {n,n(1'1(1'2)3)2} = {n,n(1'1(1(1(1... , ...2)2)2)2(1'2)2)2} n-1 вложений
εε0×3 ~~ {n,n(1'1(1'2)4)2} = {n,n(1'1(1(1(1... , ...2)2)2)2(1'2)3)2} n-1 вложений
εε0×ω = εωε0+1 ~~ {n,n(1'1(1'2)1,2)2} = {n,n(1'1(1'2)n)2}
εε0×ω+εε0 ~~ {n,n(1'1(1'2)2,2)2} = {n,n(1'1(1(1(1... , ...2)2)2)2(1'2)1,2)2} n-1 вложений
εωε0+1×2 ~~ {n,n(1'1(1'2)1,3)2} = {n,n(1'1(1'2)n,2)2}
εωε0+2 ~~ {n,n(1'1(1'2)1,1,2)2} = {n,n(1'1(1'2)n,n)2}
εωε0+ω ~~ {n,n(1'1(1'2)1(2)2)2} = {n,n(1'1(1'2)1,1,1,1,...n раз...2)2}
εωε0×2 ~~ {n,n(1'1(1'2)1(1'2)2)2} = {n,n(1'1(1'2)1(1(1(1... , ...2)2)2)2)2} n-1 вложений
εε0ω = εωωε0+1 ~~ {n,n(1'1(2'2)2)2} = {n,n(1'1(1'2)1(1'2)1(1'2)...n раз...2)2}
εωωε0+2 ~~ {n,n(1'1(3'2)2)2} = {n,n(1'1(2'2)1(2'2)1(2'2)...n раз...2)2}
εωωε0+ω ~~ {n,n(1'1(1,2'2)2)2} = {n,n(1'1(n'2)2)2}
εωωε0×2 ~~ {n,n(1'1(1(1'2)2'2)2)2} = {n,n(1'1(1(1(1(1... , ...2)2)2)2'2)2)2} n-1 вложений
εωωωε0+1 ~~ {n,n(1'1(1(1'2)1,2'2)2)2} = {n,n(1'1(1(1'2)n'2)2)2}
εωωωε0+ω ~~ {n,n(1'1(1(1'2)1(2)2'2)2)2} = {n,n(1'1(1(1'2)1,1,1,1,...n раз...2)2)2}
εωωωε0×2 ~~ {n,n(1'1(1(1'2)1(1'2)2'2)2)2} = {n,n(1'1(1(1'2)1(1(1(1... , ...2)2)2)2'2)2)2} n-1 вложений
εωωωωε0+1 ~~ {n,n(1'1(1(2'2)2'2)2)2} = {n,n(1'1(1(1'2)1(1'2)1(1'2)...n раз...2'2)2)2}
εωωωωε0+ω ~~ {n,n(1'1(1(1,2'2)2'2)2)2} = {n,n(1'1(1(n'2)2'2)2)2}
εωωωωε0×2 ~~ {n,n(1'1(1(1(1'2)2'2)2'2)2)2} = {n,n(1'1(1(1(1(1... , ...2)2)2)2'2)2'2)2)2} n-1 вложений
εε1 ~~ {n,n(1'1(1'3)2)2} = {n,n(1'1(1(1(1... , ...2'2)2'2)2'2)2)2} n-1 вложений
εε1+1 ~~ {n,n,2(1'1(1'3)2)2} = {n,{n,...{n,n(1'1(1'3)2)2}...(1'1(1'3)2)2}(1'1(1'3)2)2} n-1 вложений
εε1×2 ~~ {n,n(1'1(1'3)2)3} = {n,n(1'1(1(1(1... , ...2'2)2'2)2'2)2)2(1'1(1'3)2)2} n-1 вложений
ωεε1+1+1 ~~ {n,n(1'1(1'3)2)1,2} = {n,n(1'1(1'3)2)n}
ωεε1+1×2 ~~ {n,n(1'1(1'3)2)1(1'1(1'3)2)2} = {n,n(1'1(1'3)2)1(1'1(1(1(1... , ...2'2)2'2)2'2)2)2} n-1 вложений
ωωεε1+1 ~~ {n,n(2'2(1'3)2)2} = {n,n(1'1(1'3)2)1(1'1(1'3)2)1(1'1(1'3)2)...n-1 раз...2}
εε1+1 ~~ {n,n(1'2(1'3)2)2} = {n,n(1(1(1... , ...2'1(1'3)2)2'1(1'3)2)2'1(1'3)2)2} n-1 вложений
εε1+ε0 ~~ {n,n(1'1(1'2)2(1'3)3)2} = {n,n(1'1(1(1(1... , ...2)2)2)2(1'3)2)2} n-1 вложений
εε1×2 ~~ {n,n(1'1(1'3)3)2} = {n,n(1'1(1(1(1... , ...2'2)2'2)2'2)2(1'3)2)2} n-1 вложений
εε1×ω = εωε1+1 ~~ {n,n(1'1(1'3)1,2)2} = {n,n(1'1(1'3)n)2}
εωε1+ω ~~ {n,n(1'1(1'3)1(2)2)2} = {n,n(1'1(1'3)1,1,1,1,...n раз...2)2}
εωε1×2 ~~ {n,n(1'1(1'3)1(1'3)2)2} = {n,n(1'1(1'3)1(1(1(1... , ...2'2)2'2)2'2)2)2} n-1 вложений
εε1ω = εωωε1+1 ~~ {n,n(1'1(2'3)2)2} = {n,n(1'1(1'3)1(1'3)1(1'3)...n раз...2)2}
εωωε1+ω ~~ {n,n(1'1(1,2'3)2)2} = {n,n(1'1(n'3)2)2}
εωωε1×2 ~~ {n,n(1'1(1(1'3)2'3)2)2} = {n,n(1'1(1(1(1(1... , ...2'2)2'2)2'2)2'3)2)2} n-1 вложений
εε2 ~~ {n,n(1'1(1'4)2)2} = {n,n(1'1(1(1(1... , ...2'3)2'3)2'3)2)2} n-1 вложений
εε3 ~~ {n,n(1'1(1'5)2)2} = {n,n(1'1(1(1(1... , ...2'4)2'4)2'4)2)2} n-1 вложений
εεω ~~ {n,n(1'1(1'1,2)2)2} = {n,n(1'1(1'n)2)2}
εεω+1 ~~ {n,n(1'2(1'1,2)2)2} = {n,n(1(1(1... , ...2'1(1'1,2)2)2'1(1'1,2)2)2'1(1'1,2)2)2} n-1 вложений
εεω×2 ~~ {n,n(1'1(1'1,2)3)2} = {n,n(1'1(1'n)2(1'1,2)2)2}
εεω+1 ~~ {n,n(1'1(1'2,2)2)2} = {n,n(1'1(1(1(1(1... , ...2'1,2)2'1,2)2'1,2)2'1,2)2)2} n-1 вложений
εεω+2 ~~ {n,n(1'1(1'3,2)2)2} = {n,n(1'1(1(1(1(1... , ...2'2,2)2'2,2)2'2,2)2'2,2)2)2} n-1 вложений
εεω×2 ~~ {n,n(1'1(1'1,3)2)2} = {n,n(1'1(1'n,2)2)2}
εεω2 ~~ {n,n(1'1(1'1,1,2)2)2} = {n,n(1'1(1'n,n)2)2}
εεωω ~~ {n,n(1'1(1'1(2)2)2)2} = {n,n(1'1(1'1,1,1,1,...n раз...2)2)2}
εεε0 ~~ {n,n(1'1(1'1(1'2)2)2)2} = {n,n(1'1(1'1(1(1(1... , ...2)2)2)2)2)2} n-1 вложений
εεε0+1 ~~ {n,n(1'2(1'1(1'2)2)2)2} = {n,n(1(1(1... , ...2'1(1'1(1'2)2)2)2'1(1'1(1'2)2)2)2'1(1'1(1'2)2)2)2} n-1 вложений
εεε0+ε0 ~~ {n,n(1'1(1'2)2(1'1(1'2)2)3)2} = {n,n(1'1(1(1(1... , ...2)2)2)2(1'1(1'2)2)2)2} n-1 вложений
εεε0×2 ~~ {n,n(1'1(1'1(1'2)2)3)2} = {n,n(1'1(1'1(1(1(1... , ...2)2)2)2)2(1'1(1'2)2)2)2} n-1 вложений
ε(εε0)ω ~~ {n,n(1'1(2'1(1'2)2)2)2} = {n,n(1'1(1'1(1'2)2)1(1'1(1'2)2)1(1'1(1'2)2)...n раз...2)2}
εεε0+1 ~~ {n,n(1'1(1'2(1'2)2)2)2} = {n,n(1'1(1(1(1... , ...2'1(1'2)2)2'1(1'2)2)2'1(1'2)2)2)2} n-1 вложений
εεε0×2 ~~ {n,n(1'1(1'1(1'2)3)2)2} = {n,n(1'1(1'1(1(1(1... , ...2)2)2)2(1'2)2)2)2} n-1 вложений
εεε1 ~~ {n,n(1'1(1'1(1'3)2)2)2} = {n,n(1'1(1'1(1(1(1... , ...2'2)2'2)2'2)2)2)2} n-1 вложений
εεεω ~~ {n,n(1'1(1'1(1'1,2)2)2)2} = {n,n(1'1(1'1(1'n)2)2)2}
εεεε0 ~~ {n,n(1'1(1'1(1'1(1'2)2)2)2)2} = {n,n(1'1(1'1(1'1(1(1(1... , ...2)2)2)2)2)2)2} n-1 вложений
εεεεω ~~ {n,n(1'1(1'1(1'1(1'1,2)2)2)2)2} = {n,n(1'1(1'1(1'1(1'n)2)2)2)2}
ζ0 = φ(2,0) ~~ {n,n(1'1'2)2} = {n,n(1'1(1'1(1'1(1'1(1'1... , ...2)2)2)2)2)2} n-1 вложений
ζ0+1 ~~ {n,n,2(1'1'2)2} = {n,{n,...{n,n(1'1'2)2}...(1'1'2)2}(1'1'2)2} n-1 вложений
ζ0+ω ~~ {n,n,1,2(1'1'2)2} = {n,n,n(1'1'2)2}
ζ0×2 ~~ {n,n(1'1'2)3} = {n,n(1'1(1'1(1'1... , ...2)2)2)2(1'1'2)2} n-1 вложений
ωζ0+1 ~~ {n,n(1'1'2)1,2} = {n,n(1'1'2)n}
ωζ0×2 ~~ {n,n(1'1'2)1(1'1'2)2} = {n,n(1'1'2)1(1'1(1'1(1'1... , ...2)2)2)2} n-1 вложений
ωωζ0+1 ~~ {n,n(2'1'2)2} = {n,n(1'1'2)1(1'1'2)1(1'1'2)...n-1 раз...2}
ωωζ0+ω ~~ {n,n(1,2'1'2)2} = {n,n(n'1'2)2}
ωωζ0×2 ~~ {n,n(1(1'1'2)2'1'2)2} = {n,n(1(1'1(1'1(1'1... , ...2)2)2)2'1'2)2} n-1 вложений
ωωωζ0+1 ~~ {n,n(1(1'1'2)1,2'1'2)2} = {n,n(1(1'1'2)n'1'2)2}
ωωωζ0×2 ~~ {n,n(1(1'1'2)1(1'1'2)2'1'2)2} = {n,n(1(1'1'2)1(1'1(1'1(1'1... , ...2)2)2)2'1'2)2} n-1 вложений
ωωωωζ0+1 ~~ {n,n(1(2'1'2)2'1'2)2} = {n,n(1(1'1'2)1(1'1'2)1(1'1'2)...n раз...2'1'2)2}
ωωωωζ0×2 ~~ {n,n(1(1(1'1'2)2'1'2)2'1'2)2} = {n,n(1(1(1'1(1'1(1'1... , ...2)2)2)2'1'2)2'1'2)2} n-1 вложений
ωωωωωζ0+1 ~~ {n,n(1(1(1'1'2)1,2'1'2)2'1'2)2} = {n,n(1(1(1'1'2)n'1'2)2'1'2)2}
ωωωωωζ0×2 ~~ {n,n(1(1(1'1'2)1(1'1'2)2'1'2)2'1'2)2} = {n,n(1(1(1'1,2)1(1'1(1'1(1'1... , ...2)2)2)2'1'2)2'1'2)2} n-1 вложений
ωωωωωωζ0+1 ~~ {n,n(1(1(2'1'2)2'1'2)2'1'2)2} = {n,n(1(1(1'1'2)1(1'1'2)1(1'1'2)...n раз...2'1'2)2'1'2)2}
εζ0+1 ~~ {n,n(1'2'2)2} = {n,n(1(1(1(1... , ...2'1'2)2'1'2)2'1'2)2'1'2)2} n-1 вложений
εζ0+1+1 ~~ {n,n,2(1'2'2)2} = {n,{n,...{n,n(1'2'2)2}...(1'2'2)2}(1'2'2)2} n-1 вложений
εζ0+1+ζ0 ~~ {n,n(1'1'2)2(1'2'2)2} = {n,n(1'1(1'1(1'1... , ...2)2)2)2(1'2'2)2} n-1 вложений
εζ0+1×2 ~~ {n,n(1'2'2)3} = {n,n(1(1(1... , ...2'1'2)2'1'2)2'1'2)2(1'2'2)2} n-1 вложений
εζ0+1×2+1 ~~ {n,n,2(1'2'2)3} = {n,{n,...{n,n(1'2'2)3}...(1'2'2)3}(1'2'2)3} n-1 вложений
εζ0+1×2+ζ0 ~~ {n,n(1'1'2)2(1'2'2)3} = {n,n(1'1(1'1(1'1... , ...2)2)2)2(1'2'2)3} n-1 вложений
εζ0+1×3 ~~ {n,n(1'2'2)4} = {n,n(1(1(1... , ...2'1'2)2'1'2)2'1'2)2(1'2'2)3} n-1 вложений
ωεζ0+1+1 ~~ {n,n(1'2'2)1,2} = {n,n(1'2'2)n}
ωεζ0+1×2 ~~ {n,n(1'2'2)1(1'2'2)2} = {n,n(1'1'2)1(1(1(1... , ...2'1'2)2'1'2)2'1'2)2} n-1 вложений
ωωεζ0+1+1 ~~ {n,n(2'2'2)2} = {n,n(1'2'2)1(1'2'2)1(1'2'2)...n-1 раз...2}
ωωεζ0+1+ζ0 ~~ {n,n(1(1'1'2)2'2'2)2} = {n,n(1(1'1(1'1(1'1... , ...2)2)2)2'2'2)2} n-1 вложений
ωωεζ0+1×2 ~~ {n,n(1(1'2'2)2'2'2)2} = {n,n(1(1(1(1... , ...2'1'2)2'1'2)2'1'2)2'2'2)2} n-1 вложений
ωωεζ0+1×2+1 ~~ {n,n(2(1'2'2)2'2'2)2} = {n,n(1(1'2'2)2'2'2)1(1(1'2'2)2'2'2)1(1(1'2'2)2'2'2)...n-1 раз...2}
ωωεζ0+1×2+ζ0 ~~ {n,n(1(1'1'2)2(1'2'2)2'2'2)2} = {n,n(1(1'1(1'1(1'1... , ...2)2)2)2(1'2'2)2'2'2)2} n-1 вложений
ωωεζ0+1×3 ~~ {n,n(1(1'2'2)3'2'2)2} = {n,n(1(1(1(1... , ...2'1'2)2'1'2)2'1'2)2(1'2'2)2'2'2)2} n-1 вложений
ωωωεζ0+1+1 ~~ {n,n(1(1'2'2)1,2'2'2)2} = {n,n(1(1'2'2)n'2'2)2}
ωωωεζ0+1×2 ~~ {n,n(1(1'2'2)1(1'2'2)2'2'2)2} = {n,n(1(1'2'2)1(1(1(1... , ...2'1'2)2'1'2)2'1'2)2'2'2)2} n-1 вложений
ωωωωεζ0+1+1 ~~ {n,n(1(2'2'2)2'2'2)2} = {n,n(1(1'2'2)1(1'2'2)1(1'2'2)...n раз...2'2'2)2}
εζ0+2 ~~ {n,n(1'3'2)2} = {n,n(1(1(1(1... , ...2'2'2)2'2'2)2'2'2)2'2'2)2} n-1 вложений
εζ0+ω ~~ {n,n(1'1,2'2)2} = {n,n(1'n'2)2}
εζ0+ωω ~~ {n,n(1'1(2)2'2)2} = {n,n(1'1,1,1,1,...n раз...2'2)2}
εζ0+ε0 ~~ {n,n(1'1(1'2)2'2)2} = {n,n(1'1(1(1(1... , ...2)2)2)2'2)2} n-1 вложений
εζ0+ε1 ~~ {n,n(1'1(1'3)2'2)2} = {n,n(1'1(1(1(1... , ...2'2)2'2)2'2)2'2)2} n-1 вложений
εζ0+εε0 ~~ {n,n(1'1(1'1(1'2)2)2'2)2} = {n,n(1'1(1'1(1(1(1... , ...2)2)2)2)2'2)2} n-1 вложений
εζ0×2 ~~ {n,n(1'1(1'1'2)2'2)2} = {n,n(1'1(1'1(1'1(1'1... , ...2)2)2)2'2)2} n-1 вложений
εζ0×2+1 ~~ {n,n(1'2(1'1'2)2'2)2} = {n,n(1(1(1... , ...2'1(1'1'2)2'2)2'1(1'1'2)2'2)2'1(1'1'2)2'2)2} n-1 вложений
εζ0×3 ~~ {n,n(1'1(1'1'2)3'2)2} = {n,n(1'1(1'1(1'1(1'1... , ...2)2)2)2(1'1'2)2'2)2} n-1 вложений
εζ0×ω = εωζ0+1 ~~ {n,n(1'1(1'1'2)1,2'2)2} = {n,n(1'1(1'1'2)n'2)2}
εωζ0×2 ~~ {n,n(1'1(1'1'2)1(1'1'2)2'2)2} = {n,n(1'1(1'1'2)1(1'1(1'1(1'1... , ...2)2)2)2'2)2} n-1 вложений
εωωζ0+1 ~~ {n,n(1'1(2'1'2)2'2)2} = {n,n(1'1(1'1'2)1(1'1'2)1(1'1'2)...n раз...2'2)2}
εωωζ0×2 ~~ {n,n(1'1(1(1'1'2)2'1'2)2'2)2} = {n,n(1'1(1(1'1(1'1(1'1... , ...2)2)2)2'1'2)2'2)2} n-1 вложений
εωωωζ0+1 ~~ {n,n(1'1(1(1'1'2)1,2'1'2)2'2)2} = {n,n(1'1(1(1'1'2)n'1'2)2'2)2}
εωωωζ0×2 ~~ {n,n(1'1(1(1'1'2)1(1'1'2)2'1'2)2'2)2} = {n,n(1'1(1(1'1'2)1(1'1(1'1(1'1... , ...2)2)2)2'1'2)2'2)2} n-1 вложений
εωωωωζ0+1 ~~ {n,n(1'1(1(2'1'2)2'1'2)2'2)2} = {n,n(1'1(1(1'1'2)1(1'1'2)1(1'1'2)...n раз...2'1'2)2'2)2}
εωωωωζ0×2 ~~ {n,n(1'1(1(1(1'1'2)2'1'2)2'1'2)2'2)2} = {n,n(1'1(1(1(1'1(1'1(1'1... , ...2)2)2)2'1'2)2'1'2)2'2)2} n-1 вложений
εεζ0+1 ~~ {n,n(1'1(1'2'2)2'2)2} = {n,n(1'1(1(1(1... , ...2'1'2)2'1'2)2'1'2)2'2)2} n-1 вложений
εεζ0+1+1 ~~ {n,n(1'2(1'2'2)2'2)2} = {n,n(1(1(1... , ...2'1(1'2'2)2'2)2'1(1'2'2)2'2)2'1(1'2'2)2'2)2} n-1 вложений
εεζ0+1×2 ~~ {n,n(1'1(1'2'2)3'2)2} = {n,n(1'1(1(1(1... , ...2'1'2)2'1'2)2'1'2)2(1'2'2)2'2)2} n-1 вложений
εεζ0+1×ω ~~ {n,n(1'1(1'2'2)1,2'2)2} = {n,n(1'1(1'2'2)n'2)2}
ε(εζ0+1)2 ~~ {n,n(1'1(1'2'2)1(1'2'2)2'2)2} = {n,n(1'1(1'2'2)1(1(1(1... , ...2'1'2)2'1'2)2'1'2)2'2)2} n-1 вложений
ε(εζ0+1)ω ~~ {n,n(1'1(2'2'2)2'2)2} = {n,n(1'1(1'2'2)1(1'2'2)1(1'2'2)...n раз...2'2)2}
εεζ0+2 ~~ {n,n(1'1(1'3'2)2'2)2} = {n,n(1'1(1(1(1... , ...2'2'2)2'2'2)2'2'2)2'2)2} n-1 вложений
εεζ0+ω ~~ {n,n(1'1(1'1,2'2)2'2)2} = {n,n(1'1(1'n'2)2'2)2}
εεζ0+ε0 ~~ {n,n(1'1(1'1(1'2)2'2)2'2)2} = {n,n(1'1(1'1(1(1(1(1... , ...2)2)2)2)2'2)2'2)2} n-1 вложений
εεζ0×2 ~~ {n,n(1'1(1'1(1'1'2)2'2)2'2)2} = {n,n(1'1(1'1(1'1(1'1(1'1... , ...2)2)2)2'2)2'2)2} n-1 вложений
εεζ0×3 ~~ {n,n(1'1(1'1(1'1'2)3'2)2'2)2} = {n,n(1'1(1'1(1'1(1'1(1'1... , ...2)2)2)2(1'1'2)2'2)2'2)2} n-1 вложений
εεωζ0+1 ~~ {n,n(1'1(1'1(1'1'2)1,2'2)2'2)2} = {n,n(1'1(1'1(1'1'2)n'2)2'2)2}
εεωζ0×2 ~~ {n,n(1'1(1'1(1'1'2)1(1'1'2)2'2)2'2)2} = {n,n(1'1(1'1(1'1'2)1(1'1(1'1(1'1... , ...2)2)2)2'2)2'2)2} n-1 вложений
εεωωζ0+1 ~~ {n,n(1'1(1'1(2'1'2)2'2)2'2)2} = {n,n(1'1(1'1(1'1'2)1(1'1'2)1(1'1'2)...n раз...2'2)2'2)2}
εεωωζ0×2 ~~ {n,n(1'1(1'1(1(1'1'2)2'1'2)2'2)2'2)2} = {n,n(1'1(1'1(1(1'1(1'1(1'1... , ...2)2)2)2'1'2)2'2)2'2)2} n-1 вложений
εεεζ0+1 ~~ {n,n(1'1(1'1(1'2'2)2'2)2'2)2} = {n,n(1'1(1'1(1(1(1... , ...2'1'2)2'1'2)2'1'2)2'2)2'2)2} n-1 вложений
εεεζ0+2 ~~ {n,n(1'1(1'1(1'3'2)2'2)2'2)2} = {n,n(1'1(1'1(1(1(1... , ...2'2'2)2'2'2)2'2'2)2'2)2'2)2} n-1 вложений
εεεζ0+ω ~~ {n,n(1'1(1'1(1'1,2'2)2'2)2'2)2} = {n,n(1'1(1'1(1'n'2)2'2)2'2)2}
ζ1 ~~ {n,n(1'1'3)2} = {n,n(1'1(1'1(1'1(1'1... , ...2'2)2'2)2'2)2'2)2} n-1 вложений
εζ1+1 ~~ {n,n(1'2'3)2} = {n,n(1(1(1(1... , ...2'1'3)2'1'3)2'1'3)2'1'3)2} n-1 вложений
εζ1+ω ~~ {n,n(1'1,2'3)2} = {n,n(1'n'3)2}
εζ1+ζ0 ~~ {n,n(1'1(1'1'2)2'3)2} = {n,n(1'1(1'1(1'1(1'1(1'1... , ...2)2)2)2)2'3)2} n-1 вложений
εζ1×2 ~~ {n,n(1'1(1'1'3)2'3)2} = {n,n(1'1(1'1(1'1(1'1(1'1... , ...2'2)2'2)2'2)2'2)2'3)2} n-1 вложений
εζ1×ω = εωζ1+1 ~~ {n,n(1'1(1'1'3)1,2'3)2} = {n,n(1'1(1'1'3)n'3)2}
εωζ1×2 ~~ {n,n(1'1(1'1'3)1(1'1'3)2'3)2} = {n,n(1'1(1'1'3)1(1'1(1'1(1'1... , ...2'2)2'2)2'2)2'3)2} n-1 вложений
εωωζ1+1 ~~ {n,n(1'1(2'1'3)2'3)2} = {n,n(1'1(1'1'3)1(1'1'3)1(1'1'3)...n раз...2'3)2}
εωωζ1×2 ~~ {n,n(1'1(1(1'1'3)2'1'3)2'3)2} = {n,n(1'1(1(1'1(1'1(1'1... , ...2'2)2'2)2'2)2'1'3)2'3)2} n-1 вложений
εεζ1+1 ~~ {n,n(1'1(1'2'3)2'3)2} = {n,n(1'1(1(1(1... , ...2'1'3)2'1'3)2'1'3)2'3)2} n-1 вложений
εεζ1+ω ~~ {n,n(1'1(1'1,2'3)2'3)2} = {n,n(1'1(1'n'3)2'3)2}
εεζ1×2 ~~ {n,n(1'1(1'1(1'1'3)2'3)2'3)2} = {n,n(1'1(1'1(1'1(1'1(1'1... , ...2'2)2'2)2'2)2'3)2'3)2} n-1 вложений
εεεζ1+1 ~~ {n,n(1'1(1'1(1'2'3)2'3)2'3)2} = {n,n(1'1(1'1(1(1(1... , ...2'1'3)2'1'3)2'1'3)2'3)2'3)2} n-1 вложений
εεεζ1+ω ~~ {n,n(1'1(1'1(1'1,2'3)2'3)2'3)2} = {n,n(1'1(1'1(1'n'3)2'3)2'3)2}
ζ2 ~~ {n,n(1'1'4)2} = {n,n(1'1(1'1(1'1(1'1... , ...2'3)2'3)2'3)2'3)2} n-1 вложений
ζ3 ~~ {n,n(1'1'5)2} = {n,n(1'1(1'1(1'1(1'1... , ...2'4)2'4)2'4)2'4)2} n-1 вложений
ζω ~~ {n,n(1'1'1,2)2} = {n,n(1'1'n)2}
ζωω ~~ {n,n(1'1'1(2)2)2} = {n,n(1'1'1,1,1,1,...n раз...2)2}
ζε0 ~~ {n,n(1'1'1(1'2)2)2} = {n,n(1'1'1(1(1(1(1... , ...2)2)2)2)2)2} n-1 вложений
ζζ0 ~~ {n,n(1'1'1(1'1'2)2)2} = {n,n(1'1'1(1'1(1'1(1'1(1'1... , ...2)2)2)2)2)2} n-1 вложений
εζζ0+1 ~~ {n,n(1'2'1(1'1'2)2)2} = {n,n(1(1(1... , ...2'1'1(1'1'2)2)2'1'1(1'1'2)2)2'1'1(1'1'2)2)2} n-1 вложений
ζζ0+1 ~~ {n,n(1'1'2(1'1'2)2)2} = {n,n(1'1(1'1(1'1... , ...2'1(1'1'2)2)2'1(1'1'2)2)2'1(1'1'2)2)2} n-1 вложений
ζζ0×2 ~~ {n,n(1'1'1(1'1'2)3)2} = {n,n(1'1'1(1'1(1'1(1'1(1'1... , ...2)2)2)2)2(1'1'2)2)2} n-1 вложений
ζζ0×ω = ζωζ0+1 ~~ {n,n(1'1'1(1'1'2)1,2)2} = {n,n(1'1'1(1'1'2)n)2}
ζωζ0×2 ~~ {n,n(1'1'1(1'1'2)1(1'1'2)2)2} = {n,n(1'1'1(1'1'2)1(1'1(1'1(1'1(1'1... , ...2)2)2)2)2)2} n-1 вложений
ζωωζ0+1 ~~ {n,n(1'1'1(2'1'2)2)2} = {n,n(1'1'1(1'1'2)1(1'1'2)1(1'1'2)...n раз...2)2}
ζωωζ0×2 ~~ {n,n(1'1'1(1(1'1'2)2'1'2)2)2} = {n,n(1'1'1(1(1'1(1'1(1'1(1'1... , ...2)2)2)2)2'1'2)2)2} n-1 вложений
ζεζ0+1 ~~ {n,n(1'1'1(1'2'2)2)2} = {n,n(1'1'1(1(1(1(1... , ...2'1'2)2'1'2)2'1'2)2'1'2)2)2} n-1 вложений
ζεζ0×2 ~~ {n,n(1'1'1(1'1(1'1'2)2'2)2)2} = {n,n(1'1'1(1'1(1'1(1'1(1'1... , ...2)2)2)2'2)2)2} n-1 вложений
ζεεζ0+1 ~~ {n,n(1'1'1(1'1(1'2'2)2'2)2)2} = {n,n(1'1'1(1'1(1(1(1... , ...2'1'2)2'1'2)2'1'2)2'2)2)2} n-1 вложений
ζεεζ0×2 ~~ {n,n(1'1'1(1'1(1'1(1'1'2)2'2)2'2)2)2} = {n,n(1'1'1(1'1(1'1(1'1(1'1(1'1... , ...2)2)2)2'2)2'2)2)2} n-1 вложений
ζζ1 ~~ {n,n(1'1'1(1'1'3)2)2} = {n,n(1'1'1(1'1(1'1(1'1(1'1... , ...2'2)2'2)2'2)2'2)2)2} n-1 вложений
ζζ2 ~~ {n,n(1'1'1(1'1'4)2)2} = {n,n(1'1'1(1'1(1'1(1'1(1'1... , ...2'3)2'3)2'3)2'3)2)2} n-1 вложений
ζζω ~~ {n,n(1'1'1(1'1'1,2)2)2} = {n,n(1'1'1(1'1'n)2)2}
ζζζ0 ~~ {n,n(1'1'1(1'1'1(1'1'2)2)2)2} = {n,n(1'1'1(1'1'1(1'1(1'1(1'1(1'1... , ...2)2)2)2)2)2)2} n-1 вложений
ζζζ0+1 ~~ {n,n(1'1'2(1'1'1(1'1'2)2)2)2} = {n,n(1'1(1'1... , ...2'1(1'1'1(1'1'2)2)2)2'1(1'1'1(1'1'2)2)2)2} n-1 вложений
ζζζ0×2 ~~ {n,n(1'1'1(1'1'1(1'1'2)2)2)3} = {n,n(1'1'1(1'1'1(1'1(1'1(1'1... , ...2)2)2)2)2(1'1'1(1'1'2)2)2)3} n-1 вложений
ζζζ0+1 ~~ {n,n(1'1'1(1'1'2(1'1'2)2)2)2} = {n,n(1'1'1(1'1(1'1(1'1... , ...2'1(1'1'2)2)2'1(1'1'2)2)2'1(1'1'2)2)2)2} n-1 вложений
ζζζ0×2 ~~ {n,n(1'1'1(1'1'1(1'1'2)3)2)2} = {n,n(1'1'1(1'1'1(1'1(1'1(1'1(1'1... , ...2)2)2)2)2(1'1'2)2)2)2} n-1 вложений
ζζζ1 ~~ {n,n(1'1'1(1'1'1(1'1'3)2)2)2} = {n,n(1'1'1(1'1'1(1'1(1'1(1'1(1'1... , ...2'2)2'2)2'2)2'2)2)2)2} n-1 вложений
ζζζω ~~ {n,n(1'1'1(1'1'1(1'1'1,2)2)2)2} = {n,n(1'1'1(1'1'1(1'1'n)2)2)2}
ζζζζ0 ~~ {n,n(1'1'1(1'1'1(1'1'1(1'1'2)2)2)2)2} = {n,n(1'1'1(1'1'1(1'1'1(1'1(1'1(1'1... , ...2)2)2)2)2)2)2} n-1 вложений
ζζζζω ~~ {n,n(1'1'1(1'1'1(1'1'1(1'1'1,2)2)2)2)2} = {n,n(1'1'1(1'1'1(1'1'1(1'1'n)2)2)2)2}
η0 = φ(3,0) ~~ {n,n(1'1'1'2)2} = {n,n(1'1'1(1'1'1(1'1'1(1'1'1... , ...2)2)2)2)2} n-1 вложений
η0+1 ~~ {n,n,2(1'1'1'2)2} = {n,{n,...{n,n(1'1'1'2)2}...(1'1'1'2)2}(1'1'1'2)2} n-1 вложений
η0+ω ~~ {n,n,1,2(1'1'1'2)2} = {n,n,n(1'1'1'2)2}
η0×2 ~~ {n,n(1'1'1'2)3} = {n,n(1'1'1(1'1'1(1'1'1... , ...2)2)2)2(1'1'1'2)2} n-1 вложений
ωη0+1 ~~ {n,n(1'1'1'2)1,2} = {n,n(1'1'1'2)n}
ωη0×2 ~~ {n,n(1'1'1'2)1(1'1'1'2)2} = {n,n(1'1'1'2)1(1'1'1(1'1'1(1'1'1... , ...2)2)2)2} n-1 вложений
ωωη0+1 ~~ {n,n(2'1'1'2)2} = {n,n(1'1'1'2)1(1'1'1'2)1(1'1'1'2)...n-1 раз...2}
ωωη0+ω ~~ {n,n(1,2'1'1'2)2} = {n,n(n'1'1'2)2}
ωωη0×2 ~~ {n,n(1(1'1'1'2)2'1'1'2)2} = {n,n(1(1'1'1(1'1'1(1'1'1... , ...2)2)2)2'1'1'2)2} n-1 вложений
ωωωη0+1 ~~ {n,n(1(1'1'1'2)1,2'1'1'2)2} = {n,n(1(1'1'1'2)n'1'1'2)2}
ωωωη0×2 ~~ {n,n(1(1'1'1'2)1(1'1'1'2)2'1'1'2)2} = {n,n(1(1'1'1'2)1(1'1'1(1'1'1(1'1'1... , ...2)2)2)2'1'1'2)2} n-1 вложений
ωωωωη0+1 ~~ {n,n(1(2'1'1'2)2'1'2)2} = {n,n(1(1'1'1'2)1(1'1'1'2)1(1'1'1'2)...n раз...2'1'1'2)2}
ωωωωη0×2 ~~ {n,n(1(1(1'1'1'2)2'1'1'2)2'1'2)2} = {n,n(1(1(1'1'1(1'1'1(1'1'1... , ...2)2)2)2'1'1'2)2'1'2)2} n-1 вложений
ωωωωωη0+1 ~~ {n,n(1(1(1'1'1'2)1,2'1'1'2)2'1'1'2)2} = {n,n(1(1(1'1'1'2)n'1'1'2)2'1'1'2)2}
εη0+1 ~~ {n,n(1'2'1'2)2} = {n,n(1(1(1(1... , ...2'1'1'2)2'1'1'2)2'1'1'2)2'1'1'2)2} n-1 вложений
εη0+2 ~~ {n,n(1'3'1'2)2} = {n,n(1(1(1(1... , ...2'2'1'2)2'2'1'2)2'2'1'2)2'2'1'2)2} n-1 вложений
εη0+ω ~~ {n,n(1'1,2'1'2)2} = {n,n(1'n'1'2)2}
εη0+ε0 ~~ {n,n(1'1(1'2)2'1'2)2} = {n,n(1'1(1(1(1... , ...2)2)2)2'1'2)2} n-1 вложений
εη0+ζ0 ~~ {n,n(1'1(1'1'2)2'1'2)2} = {n,n(1'1(1'1(1'1(1'1... , ...2)2)2)2'1'2)2} n-1 вложений
εη0×2 ~~ {n,n(1'1(1'1'1'2)2'1'2)2} = {n,n(1'1(1'1'1(1'1'1(1'1'1... , ...2)2)2)2'1'2)2} n-1 вложений
εεη0+1 ~~ {n,n(1'1(1'2'1'2)2'1'2)2} = {n,n(1'1(1(1(1... , ...2'1'1'2)2'1'1'2)2'1'1'2)2'1'2)2} n-1 вложений
εεη0×2 ~~ {n,n(1'1(1'1(1'1'1'2)2'1'2)2'1'2)2} = {n,n(1'1(1'1(1'1'1(1'1'1(1'1'1... , ...2)2)2)2'1'2)2'1'2)2} n-1 вложений
εεεη0+1 ~~ {n,n(1'1(1'1(1'2'1'2)2'1'2)2'1'2)2} = {n,n(1'1(1'1(1(1(1... , ...2'1'1'2)2'1'1'2)2'1'1'2)2'1'2)2'1'2)2} n-1 вложений
ζη0+1 ~~ {n,n(1'1'2'2)2} = {n,n(1'1(1'1(1'1(1'1... , ...2'1'2)2'1'2)2'1'2)2'1'2)2} n-1 вложений
εζη0+1+1 ~~ {n,n(1'2'2'2)2} = {n,n(1(1(1(1... , ...2'1'2'2)2'1'2'2)2'1'2'2)2'1'2'2)2} n-1 вложений
ζη0+2 ~~ {n,n(1'1'3'2)2} = {n,n(1'1(1'1(1'1(1'1... , ...2'2'2)2'2'2)2'2'2)2'2'2)2} n-1 вложений
ζη0+ω ~~ {n,n(1'1'1,2'2)2} = {n,n(1'1'n'2)2}
ζη0+ε0 ~~ {n,n(1'1'1(1'2)2'2)2} = {n,n(1'1'1(1(1(1... , ...2)2)2)2'2)2} n-1 вложений
ζη0+ζ0 ~~ {n,n(1'1'1(1'1'2)2'2)2} = {n,n(1'1'1(1'1(1'1(1'1... , ...2)2)2)2'2)2} n-1 вложений
ζη0×2 ~~ {n,n(1'1'1(1'1'1'2)2'2)2} = {n,n(1'1'1(1'1'1(1'1'1(1'1'1... , ...2)2)2)2'2)2} n-1 вложений
ζεη0+1 ~~ {n,n(1'1'1(1'2'1'2)2'2)2} = {n,n(1'1'1(1(1(1... , ...2'1'1'2)2'1'1'2)2'1'1'2)2'2)2} n-1 вложений
ζζη0+1 ~~ {n,n(1'1'1(1'1'2'2)2'2)2} = {n,n(1'1'1(1'1(1'1(1'1... , ...2'1'2)2'1'2)2'1'2)2'2)2} n-1 вложений
ζζη0×2 ~~ {n,n(1'1'1(1'1'1(1'1'1'2)2'2)2'2)2} = {n,n(1'1'1(1'1'1(1'1'1(1'1'1(1'1'1... , ...2)2)2)2'2)2'2)2} n-1 вложений
ζζζη0+1 ~~ {n,n(1'1'1(1'1'1(1'1'2'2)2'2)2'2)2} = {n,n(1'1'1(1'1'1(1'1(1'1(1'1... , ...2'1'2)2'1'2)2'1'2)2'2)2'2)2} n-1 вложений
η1 ~~ {n,n(1'1'1'3)2} = {n,n(1'1'1(1'1'1(1'1'1(1'1'1... , ...2'2)2'2)2'2)2'2)2} n-1 вложений
η2 ~~ {n,n(1'1'1'4)2} = {n,n(1'1'1(1'1'1(1'1'1(1'1'1... , ...2'3)2'3)2'3)2'3)2} n-1 вложений
ηω ~~ {n,n(1'1'1'1,2)2} = {n,n(1'1'1'n)2}
ηωω ~~ {n,n(1'1'1'1(2)2)2} = {n,n(1'1'1'1,1,1,1,...n раз...2)2}
ηε0 ~~ {n,n(1'1'1'1(1'2)2)2} = {n,n(1'1'1'1(1(1(1... , ...2)2)2)2)2} n-1 вложений
ηζ0 ~~ {n,n(1'1'1'1(1'1'2)2)2} = {n,n(1'1'1'1(1'1(1'1(1'1... , ...2)2)2)2)2} n-1 вложений
ηη0 ~~ {n,n(1'1'1'1(1'1'1'2)2)2} = {n,n(1'1'1'1(1'1'1(1'1'1(1'1'1... , ...2)2)2)2)2} n-1 вложений
ηη1 ~~ {n,n(1'1'1'1(1'1'1'3)2)2} = {n,n(1'1'1'1(1'1'1(1'1'1(1'1'1... , ...2'2)2'2)2'2)2)2} n-1 вложений
ηηη0 ~~ {n,n(1'1'1'1(1'1'1'1'(1'1'1'2)2)2)2} = {n,n(1'1'1'1(1'1'1'1'(1'1'1(1'1'1(1'1'1... , ...2)2)2)2)2)2} n-1 вложений
ηηηη0 ~~ {n,n(1'1'1'1(1'1'1'1(1'1'1'1(1'1'1'2)2)2)2)2} = {n,n(1'1'1'1(1'1'1'1(1'1'1'1(1'1'1(1'1'1... , ...2)2)2)2)2)2} n-1 вложений
φ(4,0) ~~ {n,n(1'1'1'1'2)2} = {n,n(1'1'1'1(1'1'1'1(1'1'1'1(1'1'1'1(1'1'1'1... , ...2)2)2)2)2)2} n-1 вложений
φ(5,0) ~~ {n,n(1'1'1'1'1'2)2} = {n,n(1'1'1'1'1(1'1'1'1'1(1'1'1'1'1(1'1'1'1'1(1'1'1'1'1... , ...2)2)2)2)2)2} n-1 вложений
φ(ω,0) ~~ {n,n(1(2')2)2} = {n,n(1'1'1'1'1'...n раз...2)2}
φ(ω,0)+1 ~~ {n,n,2(1(2')2)2} = {n,{n,...{n,n(1(2')2)2}...(1(2')2)2}(1(2')2)2} n-1 вложений
φ(ω,0)+ω ~~ {n,n,1,2(1(2')2)2} = {n,n,n(1(2')2)2}
φ(ω,0)+ωω ~~ {n,n(2)2(1(2')2)2} = {n,n,1,1,1,1,...n-1 раз...2(1(2')2)2}
φ(ω,0)+ε0 ~~ {n,n(1'2)2(1(2')2)2} = {n,n(1(1(1... , ...2)2)2)2(1(2')2)2} n-1 вложений
φ(ω,0)+ζ0 ~~ {n,n(1'1'2)2(1(2')2)2} = {n,n(1'1(1'1(1'1... , ...2)2)2)2(1(2')2)2} n-1 вложений
φ(ω,0)+η0 ~~ {n,n(1'1'1'2)2(1(2')2)2} = {n,n(1'1'1(1'1'1(1'1'1... , ...2)2)2)2(1(2')2)2} n-1 вложений
φ(ω,0)×2 ~~ {n,n(1(2')2)3} = {n,n(1'1'1'1'1'...n раз...2)2(1(2')2)2}
ωφ(ω,0)+1 ~~ {n,n(1(2')2)1,2} = {n,n(1(2')2)n}
ωφ(ω,0)×2 ~~{n,n(1(2')2)1(1(2')2)2} = {n,n(1(2')1(1'1'1'1'1'...n раз...2)2)2}
ωωφ(ω,0)+1 ~~ {n,n(2(2')2)2} = {n,n(1(2')2)1(1(2')2)1(1(2')2)...n-1 раз...2}
ωωφ(ω,0)+ω ~~ {n,n(1,2(2')2)2} = {n,n(n(2')2)2}
ωωφ(ω,0)+ε0 ~~ {n,n(1(1'2)2(2')2)2} = {n,n(1(1(1(1... , ...2)2)2)2(2')2)2} n-1 вложений
ωωφ(ω,0)+ζ0 ~~ {n,n(1(1'1'2)2(2')2)2} = {n,n(1(1'1(1'1(1'1... , ...2)2)2)2(2')2)2} n-1 вложений
ωωφ(ω,0)+η0 ~~ {n,n(1(1'1'1'2)2(2')2)2} = {n,n(1(1'1'1(1'1'1(1'1'1... , ...2)2)2)2(2')2)2} n-1 вложений
ωωφ(ω,0)×2 ~~ {n,n(1(1(2')2)2(2')2)2} = {n,n(1(1'1'1'1'1'...n раз...2)2(2')2)2}
ωωωφ(ω,0)+1 ~~ {n,n(1(1(2')2)1,2(2')2)2} = {n,n(1(1(2')2)n(2')2)2}
ωωωφ(ω,0)×2 ~~ {n,n(1(1(2')2)1(1(2')2)2(2')2)2} = {n,n(1(1(2')2)1(1'1'1'1'1'...n раз...2)2(2')2)2}
ωωωωφ(ω,0)+1 ~~ {n,n(1(2(2')2)2(2')2)2} = {n,n(1(1(2')2)1(1(2')2)1(1(2')2)...n раз...2(2')2)2}
εφ(ω,0)+1 ~~ {n,n(1'2(2')2)2} = {n,n(1(1(1... , ...2(2')2)2(2')2)2(2')2)2} n-1 вложений
ζφ(ω,0)+1 ~~ {n,n(1'1'2(2')2)2}} = {n,n(1'1(1'1(1'1... , ...2(2')2)2(2')2)2(2')2)2} n-1 вложений
ηφ(ω,0)+1 ~~ {n,n(1'1'1'2(2')2)2} = {n,n(1'1'1(1'1'1(1'1'1... , ...2(2')2)2(2')2)2(2')2)2} n-1 вложений
φ(ω,1) ~~ {n,n(1(2')3)2} = {n,n(1'1'1'1'1'...n раз...2(2')2)2}
φ(ω,2) ~~ {n,n(1(2')4)2} = {n,n(1'1'1'1'1'...n раз...2(2')3)2}
φ(ω,ω) ~~ {n,n(1(2')1,2)2} = {n,n(1(2')n)2}
φ(ω,ω+1) ~~ {n,n(1(2')2,2)2} = {n,n(1'1'1'1'1'...n раз...2(2')1,2)2}
φ(ω,ωω) ~~ {n,n(1(2')1(2)2)2} = {n,n(1(2')1,1,1,1,...n раз...2)2}
φ(ω,ε0) ~~ {n,n(1(2')1(1'2)2)2} = {n,n(1(2')1(1(1(1... , ...2)2)2)2)2} n-1 вложений
φ(ω,ε1) ~~ {n,n(1(2')1(1'3)2)2} = {n,n(1(2')1(1(1(1... , ...2'2)2'2)2'2)2)2} n-1 вложений
φ(ω,ζ0) ~~ {n,n(1(2')1(1'1'2)2)2} = {n,n(1(2')1(1'1(1'1(1'1... , ...2)2)2)2)2} n-1 вложений
φ(ω,η0) ~~ {n,n(1(2')1(1'1'1'2)2)2} = {n,n(1(2')1(1'1'1(1'1'1(1'1'1... , ...2)2)2)2)2} n-1 вложений
φ(ω,φ(ω,0)) ~~ {n,n(1(2')1(1(2')2)2)2} = {n,n(1(2')1(1'1'1'1'...n раз...2)2)2}
φ(ω,φ(ω,0)+1) ~~ {n,n(1(2')2(1(2')2)2)2} = {n,n(1(1'1'1'1'...n раз...2)2(2')1(1(2')2)2)2}
φ(ω,φ(ω,0)+ω) ~~ {n,n(1(2')1,2(1(2')2)2)2} = {n,n(1(2')n(1(2')2)2)2}
φ(ω,φ(ω,0)+ε0) ~~ {n,n(1(2')1(1'2)2(1(2')2)2)2} = {n,n(1(2')1(1(1(1... , ...2)2)2)2(1(2')2)2)2} n-1 вложений
φ(ω,φ(ω,0)×2) ~~ {n,n(1(2')1(1(2')2)3)2} = {n,n(1(2')1(1'1'1'1'...n раз...2)2(1(2')2)2)2}
φ(ω,ωφ(ω,0)+1) ~~ {n,n(1(2')1(1(2')2)1,2)2} = {n,n(1(2')1(1(2')2)n)2}
φ(ω,ωφ(ω,0)×2) ~~ {n,n(1(2')1(1(2')2)1(1(2')2)2)2} = {n,n(1(2')1(1(2')2)1(1'1'1'1'...n раз...2)2)2}
φ(ω,ωωφ(ω,0)+1) ~~ {n,n(1(2')1(2(2')2)2)2} = {n,n(1(2')1(1(2')2)1(1(2')2)1(1(2')2)...n раз...2)2}
φ(ω,εφ(ω,0)+1) ~~ {n,n(1(2')1(1'2(2')2)2)2} = {n,n(1(2')1(1(1(1... , ...2(2')2)2(2')2)2(2')2)2)2} n-1 вложений
φ(ω,ζφ(ω,0)+1) ~~ {n,n(1(2')1(1'1'2(2')2)2)2} = {n,n(1(2')1(1'1(1'1(1'1... , ...2(2')2)2(2')2)2(2')2)2)2} n-1 вложений
φ(ω,ηφ(ω,0)+1) ~~ {n,n(1(2')1(1'1'1'2(2')2)2)2} = {n,n(1(2')1(1'1'1(1'1'1(1'1'1... , ...2(2')2)2(2')2)2(2')2)2)2} n-1 вложений
φ(ω,φ(ω,1)) ~~ {n,n(1(2')1(1(2')3)2)2} = {n,n(1(2')1(1'1'1'1'...n раз...2(2')2)2)2}
φ(ω,φ(ω,ω)) ~~ {n,n(1(2')1(1(2')1,2)2)2} = {n,n(1(2')1(1(2')n)2)2}
φ(ω,φ(ω,φ(ω,0))) ~~ {n,n(1(2')1(1(2')1(1(2')2)2)2)2} = {n,n(1(2')1(1(2')1(1'1'1'1'...n раз...2)2)2)2}
φ(ω,φ(ω,φ(ω,1))) ~~ {n,n(1(2')1(1(2')1(1(2')3)2)2)2} = {n,n(1(2')1(1(2')1(1'1'1'1'...n раз...2(2')2)2)2)2}
φ(ω,φ(ω,φ(ω,ω))) ~~ {n,n(1(2')1(1(2')1(1(2')1,2)2)2)2} = {n,n(1(2')1(1(2')1(1(2')n)2)2)2}
φ(ω,φ(ω,φ(ω,φ(ω,0)))) ~~ {n,n(1(2')1(1(2')1(1(2')1(1(2')2)2)2)2)2} = {n,n(1(2')1(1(2')1(1(2')1(1'1'1'1'...n раз...2)2)2)2)2}
φ(ω+1,0) ~~ {n,n(1(2')1'2)2} = {n,n(1(2')1(1(2')1(1(2')1(1(2')1... , ...2)2)2)2)2} n-1 вложений
εφ(ω+1,0)+1 ~~ {n,n(1'2(2')1'2)2} = {n,n(1(1(1... , ...2(2')1'2)2(2')1'2)2(2')1'2)2} n-1 вложений
ζφ(ω+1,0)+1 ~~ {n,n(1'1'2(2')1'2)2} = {n,n(1'1(1'1(1'1... , ...2(2')1'2)2(2')1'2)2(2')1'2)2} n-1 вложений
φ(ω,φ(ω+1,0)+1) ~~ {n,n(1(2')2'2)2} = {n,n(1'1'1'1'...n раз...2(2')1'2)2}
φ(ω+1,1) ~~ {n,n(1(2')1'3)2} = {n,n(1(2')1(1(2')1(1(2')1(1(2')1... , ...2'2)2'2)2'2)2'2)2} n-1 вложений
φ(ω+1,ω) ~~ {n,n(1(2')1'1,2)2} = {n,n(1(2')1'n)2}
φ(ω+1,φ(ω,0)) ~~ {n,n(1(2')1'1(1(2')2)2)2} = {n,n(1(2')1'1(1'1'1'1'1'...n раз...2)2)2}
φ(ω+1,φ(ω+1,0)) ~~ {n,n(1(2')1'1(1(2')1'2)2)2} = {n,n(1(2')1'1(1(2')1(1(2')1(1(2')1... , ...2)2)2)2)2} n-1 вложений
φ(ω+1,φ(ω+1,1)) ~~ {n,n(1(2')1'1(1(2')1'3)2)2} = {n,n(1(2')1'1(1(2')1(1(2')1(1(2')1... , ...2'2)2'2)2'2)2)2} n-1 вложений
φ(ω+1,φ(ω+1,ω)) ~~ {n,n(1(2')1'1(1(2')1'1,2)2)2} = {n,n(1(2')1'1(1(2')1'n)2)2}
φ(ω+2,0) ~~ {n,n(1(2')1'1'2)2} = {n,n(1(2')1'1(1(2')1'1(1(2')1'1... , ...2)2)2)2} n-1 вложений
φ(ω+3,0) ~~ {n,n(1(2')1'1'1'2)2} = {n,n(1(2')1'1'1(1(2')1'1'1(1(2')1'1'1... , ...2)2)2)2} n-1 вложений
φ(ω×2,0) ~~ {n,n(1(2')1(2')2)2} = {n,n(1(2')1'1'1'1'...n раз...2)2}
φ(ω×2,1) ~~ {n,n(1(2')1(2')3)2} = {n,n(1(2')1'1'1'1'...n раз...2(2')2)2}
φ(ω×2,ω) ~~ {n,n(1(2')1(2')1,2)2} = {n,n(1(2')1(2')n)2}
φ(ω×2+1,0) ~~ {n,n(1(2')1(2')1'2)2} = {n,n(1(2')1(2')1(1(2')1(2')1... , ...2)2)2} n-1 вложений
φ(ω×3,0) ~~ {n,n(1(2')1(2')1(2')2)2} = {n,n(1(2')1(2')1'1'1'1'...n раз...2)2}
φ(ω×4,0) ~~ {n,n(1(2')1(2')1(2')1(2')2)2} = {n,n(1(2')1(2')1(2')1'1'1'1'...n раз...2)2}
φ(ω2,0) ~~ {n,n(1(3')2)2} = {n,n(1(2')1(2')1(2')1(2')...n раз...2)2}
φ(ω3,0) ~~ {n,n(1(4')2)2} = {n,n(1(3')1(3')1(3')1(3')...n раз...2)2}
φ(ωω,0) ~~ {n,n(1(1,2')2)2} = {n,n(1(n')2)2}
φ(ωωω,0) ~~ {n,n(1(1(2)2')2)2} = {n,n(1(1,1,1,1,...n раз...2')2)2}
φ(ωωωω,0) ~~ {n,n(1(1(1,2)2')2)2} = {n,n(1(1(n)2')2)2}
φ(ωωωωω,0) ~~ {n,n(1(1(1(2)2)2')2)2} = {n,n(1(1(1,1,1,1,...n раз...2)2')2)2}
φ(ε0,0) ~~ {n,n(1(1(1'2)2')2)2} = {n,n(1(1(1(1(1... , ...2)2)2)2')2)2} n-1 вложений
φ(ε1,0) ~~ {n,n(1(1(1'3)2')2)2} = {n,n(1(1(1(1(1... , ...2'2)2'2)2'2)2')2)2} n-1 вложений
φ(ζ0,0) ~~ {n,n(1(1(1'1'2)2')2)2} = {n,n(1(1(1'1(1'1(1'1... , ...2)2)2)2')2)2} n-1 вложений
φ(η0,0) ~~ {n,n(1(1(1'1'1'2)2')2)2} = {n,n(1(1(1'1'1(1'1'1(1'1'1... , ...2)2)2)2')2)2} n-1 вложений
φ(φ(4,0),0) ~~ {n,n(1(1(1'1'1'1'2)2')2)2} = {n,n(1(1(1'1'1'1(1'1'1'1(1'1'1'1... , ...2)2)2)2')2)2} n-1 вложений
φ(φ(ω,0),0) ~~ {n,n(1(1(1(2')2)2')2)2} = {n,n(1(1(1'1'1'1'...n раз...2)2')2)2} n-1 вложений
φ(φ(ω+1,0),0) ~~ {n,n(1(1(1(2')1'2)2')2)2} = {n,n(1(1(1(2')1(1(2')1(1(2')1(1(2')1... , ...2)2)2)2)2')2)2} n-1 вложений
φ(φ(ω×2,0),0) ~~ {n,n(1(1(1(2')1(2')2)2')2)2} = {n,n(1(1(1(2')1'1'1'1'...n раз...2)2')2)2}
φ(φ(ω2,0),0) ~~ {n,n(1(1(1(3')2)2')2)2} = {n,n(1(1(1(2')1(2')1(2')1(2')...n раз...2)2')2)2}
φ(φ(ωω,0),0) ~~ {n,n(1(1(1(1,2')2)2')2)2} = {n,n(1(1(1(n')2)2')2)2}
φ(φ(ε0,0),0) ~~ {n,n(1(1(1(1(1'2)2')2)2')2)2} = {n,n(1(1(1(1(1(1(1... , ...2)2)2)2')2)2')2)2} n-1 вложений
φ(φ(ζ0,0),0) ~~ {n,n(1(1(1(1(1'1'2)2')2)2')2)2} = {n,n(1(1(1(1(1'1(1'1(1'1... , ...2)2)2)2')2)2')2)2} n-1 вложений
φ(φ(φ(ω,0),0),0) ~~ {n,n(1(1(1(1(1(2')2)2')2)2')2)2} = {n,n(1(1(1(1(1'1'1'1'...n раз...2)2')2)2')2)2}
φ(φ(φ(ωω,0),0),0) ~~ {n,n(1(1(1(1(1(1,2')2)2')2)2')2)2} = {n,n(1(1(1(1(1(n')2)2')2)2')2)2}
φ(φ(φ(ε0,0),0),0) ~~ {n,n(1(1(1(1(1(1(1'2)2')2)2')2)2')2)2} = {n,n(1(1(1(1(1(1(1(1(1... , ...2)2)2)2')2)2')2)2')2)2} n-1 вложений
φ(φ(φ(φ(ω,0),0),0),0) ~~ {n,n(1(1(1(1(1(1(1(2')2)2')2)2')2)2')2)2} = {n,n(1(1(1(1(1(1(1'1'1'1'...n раз...2)2')2)2')2)2')2)2}
φ(φ(φ(φ(ωω,0),0),0),0) ~~ {n,n(1(1(1(1(1(1(1(1,2')2)2')2)2')2)2')2)2} = {n,n(1(1(1(1(1(1(1(n')2)2')2)2')2)2')2)2}
Г0 = φ(1,0,0) = ψ(ΩΩ) ~~ {n,n(1(1'2')2)2} = {n,n(1(1(1(1(1(1(1(1... , ...2')2)2')2)2')2)2')2)2} n-1 вложений
Г0+1 ~~ {n,n,2(1(1'2')2)2} = {n,{n,...{n,n(1(1'2')2)2}...(1(1'2')2)2}(1(1'2')2)2} n-1 вложений
Г0+ω ~~ {n,n,1,2(1(1'2')2)2} = {n,n,n(1(1'2')2)2}
Г0+ωω ~~ {n,n(2)2(1(1'2')2)2} = {n,n,1,1,1,1,...n-1 раз...2(1(1'2')2)2}
Г0+ωωω ~~ {n,n(1,2)2(1(1'2')2)2} = {n,n(n)2(1(1'2')2)2}
Г0+ε0 ~~ {n,n(1'2)2(1(1'2')2)2} = {n,n(1(1(1... , ...2)2)2)2(1(1'2')2)2} n-1 вложений
Г0×2 ~~ {n,n(1(1'2')2)3} = {n,n(1(1(1(1(1(1... , ...2')2)2')2)2')2)2(1(1'2')2)2} n-1 вложений
Г0×3 ~~ {n,n(1(1'2')2)4} = {n,n(1(1(1(1(1(1... , ...2')2)2')2)2')2)2(1(1'2')2)3} n-1 вложений
ωГ0+1 ~~ {n,n(1(1'2')2)1,2} = {n,n(1(1'2')2)n}
ωГ0×2 ~~ {n,n(1(1'2')2)1(1(1'2')2)2} = {n,n(1(1'2')2)1(1(1(1(1(1(1... , ...2')2)2')2)2')2)2} n-1 вложений
ωωГ0+1 ~~ {n,n(2(1'2')2)2} = {n,n(1(1'2')2)1(1(1'2')2)1(1(1'2')2)...n-1 раз...2}
ωωГ0+ω ~~ {n,n(1,2(1'2')2)2} = {n,n(n(1'2')2)2}
ωωГ0+ωω ~~ {n,n(1(2)2(1'2')2)2} = {n,n(1,1,1,...n раз...2(1'2')2)2}
ωωГ0+ωωω ~~ {n,n(1(1,2)2(1'2')2)2} = {n,n(1(n)2(1'2')2)2}
ωωГ0+ε0 ~~ {n,n(1(1'2)2(1'2')2)2} = {n,n(1(1(1(1... , ...2)2)2)2(1'2')2)2} n-1 вложений
ωωГ0×2 ~~ {n,n(1(1(1'2')2)2(1'2')2)2} = {n,n(1(1(1(1(1(1(1... , ...2')2)2')2)2')2)2(1'2')2)2} n-1 вложений
ωωГ0×3 ~~ {n,n(1(1(1'2')2)3(1'2')2)2} = {n,n(1(1(1(1(1(1(1... , ...2')2)2')2)2')2)2(1(1'2')2)2(1'2')2)2} n-1 вложений
ωωωГ0+1 ~~ {n,n(1(1(1'2')2)1,2(1'2')2)2} = {n,n(1(1(1'2')2)n(1'2')2)2}
ωωωГ0×2 ~~ {n,n(1(1(1'2')2)1(1(1'2')2)2(1'2')2)2} = {n,n(1(1(1'2')2)1(1(1(1(1(1(1... , ...2')2)2')2)2')2)2(1'2')2)2} n-1 вложений
ωωωωГ0+1 ~~ {n,n(1(2(1'2')2)2(1'2')2)2} = {n,n(1(1(1'2')2)1(1(1'2')2)1(1(1'2')2)...n раз...2(1'2')2)2}
φ(1,Г0+1) ~~ {n,n(1'2(1'2')2)2} = {n,n(1(1(1... , ...2(1'2')2)2(1'2')2)2(1'2')2)2} n-1 вложений
φ(2,Г0+1) ~~ {n,n(1'1'2(1'2')2)2} = {n,n(1'1(1'1(1'1... , ...2(1'2')2)2(1'2')2)2(1'2')2)2} n-1 вложений
φ(3,Г0+1) ~~ {n,n(1'1'1'2(1'2')2)2} = {n,n(1'1'1(1'1'1(1'1'1... , ...2(1'2')2)2(1'2')2)2(1'2')2)2} n-1 вложений
φ(ω,Г0+1) ~~ {n,n(1(2')2(1'2')2)2} = {n,n(1'1'1'...n раз...2(1'2')2)2}
φ(ωω,Г0+1) ~~ {n,n(1(1,2')2(1'2')2)2} = {n,n(1(n')2(1'2')2)2}
φ(ε0,Г0+1) ~~ {n,n(1(1(1'2)2')2(1'2')2)2} = {n,n(1(1(1(1(1... , ...2)2)2)2')2(1'2')2)2} n-1 вложений
φ(ζ0,Г0+1) ~~ {n,n(1(1(1'1'2)2')2(1'2')2)2} = {n,n(1(1(1'1(1'1(1'1... , ...2)2)2)2')2(1'2')2)2} n-1 вложений
φ(φ(ω,0),Г0+1) ~~ {n,n(1(1(1(2')2)2')2(1'2')2)2} = {n,n(1(1(1'1'1'...n раз...2)2')2(1'2')2)2}
φ(φ(ωω,0),Г0+1) ~~ {n,n(1(1(1(1,2')2)2')2(1'2')2)2} = {n,n(1(1(1(n')2)2')2(1'2')2)2}
φ(φ(ε0,0),Г0+1) ~~ {n,n(1(1(1(1(1'2)2')2)2')2(1'2')2)2} = {n,n(1(1(1(1(1(1(1... , ...2)2)2)2')2)2')2(1'2')2)2} n-1 вложений
φ(φ(ζ0,0),Г0+1) ~~ {n,n(1(1(1(1(1'1'2)2')2)2')2(1'2')2)2} = {n,n(1(1(1(1(1'1(1'1(1'1... , ...2)2)2)2')2)2')2(1'2')2)2} n-1 вложений
φ(φ(φ(ω,0),0),Г0+1) ~~ {n,n(1(1(1(1(1(2')2)2')2)2')2(1'2')2)2} = {n,n(1(1(1(1(1'1'1'...n раз...2)2')2)2')2(1'2')2)2}
φ(φ(φ(ωω,0),0),Г0+1) ~~ {n,n(1(1(1(1(1(1,2')2)2')2)2')2(1'2')2)2} = {n,n(1(1(1(1(1(n')2)2')2)2')2(1'2')2)2}
φ(Г0,1) ~~ {n,n(1(1(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1(1(1(1(1... , ...2')2)2')2)2')2)2')2(1'2')2)2} n-1 вложений
φ(1,φ(Г0,1)+1) ~~ {n,n(1'2(1(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1... , ...(1(1(1'2')2)2')2(1'2')2)(1(1(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(ω,φ(Г0,1)+1) ~~ {n,n(1(2')2(1(1(1'2')2)2')2(1'2')2)2} = {n,n(1'1'1'...n раз...2(1(1(1'2')2)2')2(1'2')2)2}
φ(ωω,φ(Г0,1)+1) ~~ {n,n(1(1,2')2(1(1(1'2')2)2')2(1'2')2)2} = {n,n(1(n')2(1(1(1'2')2)2')2(1'2')2)2}
φ(ε0,φ(Г0,1)+1) ~~ {n,n(1(1(1'2)2')2(1(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1... , ...2)2)2')2(1(1(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(φ(ω,0),φ(Г0,1)+1) ~~ {n,n(1(1(1(2')2)2')2(1(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1'1'1'...n раз...2)2')2(1(1(1'2')2)2')2(1'2')2)2}
φ(φ(ωω,0),φ(Г0,1)+1) ~~ {n,n(1(1(1(1,2')2)2')2(1(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(n')2)2')2(1(1(1'2')2)2')2(1'2')2)2}
φ(Г0,2) ~~ {n,n(1(1(1(1'2')2)2')3(1'2')2)2} = {n,n(1(1(1(1(1(1... , ...2')2)2')2)2')2(1(1(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(Г0,3) ~~ {n,n(1(1(1(1'2')2)2')4(1'2')2)2} = {n,n(1(1(1(1(1(1... , ...2')2)2')2)2')2(1(1(1'2')2)2')3(1'2')2)2} n-1 вложений
φ(Г0,ω) ~~ {n,n(1(1(1(1'2')2)2')1,2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')n(1'2')2)2} n-1 вложений
φ(Г0,ε0) ~~ {n,n(1(1(1(1'2')2)2')1(1'2)2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(1(1... , ...2)2)2(1'2')2)2} n-1 вложений
φ(Г0,ζ0) ~~ {n,n(1(1(1(1'2')2)2')1(1'1'2)2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(1'1(1'1... , ...2)2)2(1'2')2)2} n-1 вложений
φ(Г0,η0) ~~ {n,n(1(1(1(1'2')2)2')1(1'1'1'2)2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(1'1'1(1'1'1... , ...2)2)2(1'2')2)2} n-1 вложений
φ(Г0,φ(ω,0)) ~~ {n,n(1(1(1(1'2')2)2')1(1(2')2)2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(1'1'1'...n раз...2)2(1'2')2)2}
φ(Г0,φ(φ(ω,0),0)) ~~ {n,n(1(1(1(1'2')2)2')1(1(1(1(2')2)2')2)2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(1(1(1'1'1'...n раз...2)2')2)2(1'2')2)2}
φ(Г0,Г0) ~~ {n,n(1(1(1(1'2')2)2')1(1(1'2')2)2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(1(1(1(1... , ...2')2)2')2)2(1'2')2)2} n-1 вложений
φ(Г0,Г0+1) ~~ {n,n(1(1(1(1'2')2)2')2(1(1'2')2)2(1'2')2)2}
= {n,n(1(1(1(1(1(1... , ...2')2)2')2)2')2(1(1(1'2')2)2')1(1(1'2')2)2(1'2')2)2} n-1 вложений
φ(Г0,Г0×2) ~~ {n,n(1(1(1(1'2')2)2')1(1(1'2')2)3(1'2')2)2}
= {n,n(1(1(1(1'2')2)2')1(1(1(1(1... , ...2')2)2')2)2(1(1'2')2)2(1'2')2)2} n-1 вложений
φ(Г0,ωГ0+1) ~~ {n,n(1(1(1(1'2')2)2')1(1(1'2')2)1,2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(1(1'2')2)n(1'2')2)2}
φ(Г0,ωГ0×2) ~~ {n,n(1(1(1(1'2')2)2')1(1(1'2')2)1(1(1'2')2)2(1'2')2)2}
= {n,n(1(1(1(1'2')2)2')1(1(1'2')2)1(1(1(1(1... , ...2')2)2')2)2(1'2')2)2} n-1 вложений
φ(Г0,ωωГ0+1) ~~ {n,n(1(1(1(1'2')2)2')1(2(1'2')2)2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(1(1'2')2)1(1(1'2')2)...n раз...2(1'2')2)2}
φ(Г0,φ(1,Г0+1)) ~~ {n,n(1(1(1(1'2')2)2')1(1'2(1'2')2)2(1'2')2)2}
= {n,n(1(1(1(1'2')2)2')1(1(1(1... , ...2(1'2')2)2(1'2')2)2(1'2')2)2(1'2')2)2} n-1 вложений
φ(Г0,φ(Г0,1)) ~~ {n,n(1(1(1(1'2')2)2')1(1(1(1(1'2')2)2')2(1'2')2)2(1'2')2)2}
= {n,n(1(1(1(1'2')2)2')1(1(1(1(1(1(1... , ...2')2)2')2)2')2(1'2')2)2(1'2')2)2} n-1 вложений
φ(Г0,φ(Г0,Г0)) ~~ {n,n(1(1(1(1'2')2)2')1(1(1(1(1'2')2)2')1(1(1'2')2)2(1'2')2)2(1'2')2)2}
= {n,n(1(1(1(1'2')2)2')1(1(1(1(1'2')2)2')1(1(1(1(1... , ...2')2)2')2)2(1'2')2)2} n-1 вложений
φ(Г0+1,0) ~~ {n,n(1(1(1(1'2')2)2')1'2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(1(1(1(1'2')2)2')1... , ...2(1'2')2)2(1'2')2)2} n-1 вложений
φ(1,φ(Г0+1,0)+1) ~~ {n,n(1'2(1(1(1'2')2)2')1'2(1'2')2)2}
= {n,n(1(1... , ...2(1(1(1'2')2)2')1'2(1'2')2)2(1(1(1'2')2)2')1'2(1'2')2)2} n-1 вложений
φ(Г0,φ(Г0+1,0)+1) ~~ {n,n(1(1(1(1'2')2)2')2'2(1'2')2)2}
= {n,n(1(1(1(1(1(1... , ...2')2)2')2)2')2(1(1(1'2')2)2')1'2(1'2')2)2} n-1 вложений
φ(Г0+1,1) ~~ {n,n(1(1(1(1'2')2)2')1'3(1'2')2)2}
= {n,n(1(1(1(1'2')2)2')1(1(1(1(1'2')2)2')1... , ...2'2(1'2')2)2'2(1'2')2)2} n-1 вложений
φ(Г0+1,Г0) ~~ {n,n(1(1(1(1'2')2)2')1'1(1(1'2')2)2(1'2')2)2}
= {n,n(1(1(1(1'2')2)2')1'1(1(1(1(1... , ...2')2)2')2)2(1'2')2)2} n-1 вложений
φ(Г0+2,0) ~~ {n,n(1(1(1(1'2')2)2')1'1'2(1'2')2)2}
= {n,n(1(1(1(1'2')2)2')1'1(1(1(1(1'2')2)2')1'1... , ...2(1'2')2)2(1'2')2)2} n-1 вложений
φ(Г0+ω,0) ~~ {n,n(1(1(1(1'2')2)2')1(2')2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1'1'1'...n раз...2(1'2')2)2}
φ(Г0+ωω,0) ~~ {n,n(1(1(1(1'2')2)2')1(1,2')2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(n')2(1'2')2)2}
φ(Г0+ε0,0) ~~ {n,n(1(1(1(1'2')2)2')1(1(1'2)2')2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(1(1(1(1... , ...2)2)2)2')2(1'2')2)2} n-1 вложений
φ(Г0+φ(ω,0),0) ~~ {n,n(1(1(1(1'2')2)2')1(1(1(2')2)2')2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(1(1'1'1'...n раз...2)2')2(1'2')2)2}
φ(Г0+φ(ωω,0),0) ~~ {n,n(1(1(1(1'2')2)2')1(1(1(1,2')2)2')2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(1(1(n')2)2')2(1'2')2)2}
φ(Г0+φ(φ(ω,0),0),0) ~~ {n,n(1(1(1(1'2')2)2')1(1(1(1(1(2')2)2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1'2')2)2')1(1(1(1(1'1'1'...n раз...2)2')2)2')2(1'2')2)2}
φ(Г0+φ(φ(ωω,0),0),0) ~~ {n,n(1(1(1(1'2')2)2')1(1(1(1(1(1,2')2)2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1'2')2)2')1(1(1(1(1(n')2)2')2)2')2(1'2')2)2}
φ(Г0×2,0) ~~ {n,n(1(1(1(1'2')2)2')1(1(1(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1'2')2)2')1(1(1(1(1(1... , ...2')2)2')2)2')2(1'2')2)2} n-1 вложений
φ(Г0×2+1,0) ~~ {n,n(1(1(1(1'2')2)2')1(1(1(1'2')2)2')1'2(1'2')2)2}
= {n,n(1(1(1(1'2')2)2')1(1(1(1'2')2)2')1(1(1(1(1'2')2)2')1(1(1(1'2')2)2')1... , ...2(1'2')2)2(1'2')2)2} n-1 вложений
φ(Г0×3,0) ~~ {n,n(1(1(1(1'2')2)2')1(1(1(1'2')2)2')1(1(1(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1'2')2)2')1(1(1(1'2')2)2')1(1(1(1(1(1... , ...2')2)2')2)2')2(1'2')2)2} n-1 вложений
φ(ωГ0+1,0) ~~ {n,n(1(2(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1'2')2)2')1(1(1(1'2')2)2')...n раз...2(1'2')2)2}
φ(ωГ0+ω,0) ~~ {n,n(1(1,2(1(1'2')2)2')2(1'2')2)2} = {n,n(1(n(1(1'2')2)2')2(1'2')2)2}
φ(ωГ0+ε0,0) ~~ {n,n(1(1(1'2)2(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1(1... , ...2)2)2)2(1(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(ωГ0+φ(ω,0),0) ~~ {n,n(1(1(1(2')2)2(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1'1'1'...n раз...2)2(1(1'2')2)2')2(1'2')2)2}
φ(ωГ0+φ(ωω,0),0) ~~ {n,n(1(1(1(1,2')2)2(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(n')2)2(1(1'2')2)2')2(1'2')2)2}
φ(ωГ0+φ(φ(ωω,0)0),0) ~~ {n,n(1(1(1(1(1(1,2')2)2')2)2(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1(1(n')2)2')2)2(1(1'2')2)2')2(1'2')2)2}
φ(ωГ0×2,0) ~~ {n,n(1(1(1(1'2')2)3')2(1'2')2)2} = {n,n(1(1(1(1(1(1... , ...2')2)2')2)2(1(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(ωГ0×3,0) ~~ {n,n(1(1(1(1'2')2)4')2(1'2')2)2} = {n,n(1(1(1(1(1(1... , ...2')2)2')2)2(1(1'2')2)3')2(1'2')2)2} n-1 вложений
φ(ωωГ0+1,0) ~~ {n,n(1(1(1(1'2')2)1,2')2(1'2')2)2} = {n,n(1(1(1(1'2')2)n')2(1'2')2)2}
φ(ωωГ0×2,0) ~~ {n,n(1(1(1(1'2')2)1(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1'2')2)1(1(1(1(1... , ...2')2)2')2)2')2(1'2')2)2} n-1 вложений
φ(ωωωГ0+1,0) ~~ {n,n(1(1(2(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1'2')2)1(1(1'2')2)...n раз...2')2(1'2')2)2}
φ(ωωωГ0+ω,0) ~~ {n,n(1(1(1,2(1'2')2)2')2(1'2')2)2} = {n,n(1(1(n(1'2')2)2')2(1'2')2)2}
φ(ωωωГ0×2,0) ~~ {n,n(1(1(1(1(1'2')2)2(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1(1(1(1... , ...2')2)2')2)2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(φ(1,Г0+1),0) ~~ {n,n(1(1(1'2(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1(1... , ...2(1'2')2)2(1'2')2)2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(φ(ω,Г0+1),0) ~~ {n,n(1(1(2')2(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1'1'1'...n раз...2(1(1'2')2)2')2(1'2')2)2}
φ(φ(ωω,Г0+1),0) ~~ {n,n(1(1(1,2')2(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1(n')2(1(1'2')2)2')2(1'2')2)2}
φ(φ(φ(ω,0),Г0+1),0) ~~ {n,n(1(1(1(1(2')2)2')2(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1'1'1'...n раз...2)2')2(1(1'2')2)2')2(1'2')2)2}
φ(φ(Г0,1),0) ~~ {n,n(1(1(1(1(1(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1(1(1(1(1... , ...2')2)2')2)2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(φ(Г0,1),1) ~~ {n,n(1(1(1(1(1(1'2')2)2')2(1'2')2)2')3(1'2')2)2}
= {n,n(1(1(1(1(1(1(1(1... , ...2')2)2')2)2')2(1'2')2)2')2(1(1(1(1(1'2')2)2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(φ(Г0,1),ω) ~~ {n,n(1(1(1(1(1(1'2')2)2')2(1'2')2)2')1,2(1'2')2)2} = {n,n(1(1(1(1(1(1'2')2)2')2(1'2')2)2')n(1'2')2)2}
φ(φ(Г0,1)+1,0) ~~ {n,n(1(1(1(1(1(1'2')2)2')2(1'2')2)2')1'2(1'2')2)2}
= {n,n(1(1(1(1(1(1'2')2)2')2(1'2')2)2')1(1(1(1(1(1'2')2)2')2(1'2')2)2')1... , ...2(1'2')2)2(1'2')2)2} n-1 вложений
φ(φ(Г0,1)×2,0) ~~ {n,n(1(1(1(1(1(1'2')2)2')2(1'2')2)2')1(1(1(1(1(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1(1(1'2')2)2')2(1'2')2)2')1(1(1(1(1(1(1(1... , ...2')2)2')2)2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(ωφ(Г0,1)+1,0) ~~ {n,n(1(2(1(1(1(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1(1(1'2')2)2')2(1'2')2)2')1(1(1(1(1(1'2')2)2')2(1'2')2)2')...n раз...2(1'2')2)2}
φ(ωφ(Г0,1)×2,0) ~~ {n,n(1(1(1(1(1(1'2')2)2')2(1'2')2)3')2(1'2')2)2}
= {n,n(1(1(1(1(1(1(1(1... , ...2')2)2')2)2')2(1'2')2)2(1(1(1(1'2')2)2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(ωωφ(Г0,1)+1,0) ~~ {n,n(1(1(1(1(1(1'2')2)2')2(1'2')2)1,2')2(1'2')2)2} = {n,n(1(1(1(1(1(1'2')2)2')2(1'2')2)n')2(1'2')2)2}
φ(ωωωφ(Г0,1)+1,0) ~~ {n,n(1(1(2(1(1(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1(1(1'2')2)2')2(1'2')2)1(1(1(1(1'2')2)2')2(1'2')2)...n раз...2')2(1'2')2)2}
φ(φ(1,φ(Г0,1)+1),0) ~~ {n,n(1(1(1'2(1(1(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1... , ...2(1(1(1'2')2)2')2(1'2')2)2(1(1(1'2')2)2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(φ(Г0,2),0) ~~ {n,n(1(1(1(1(1(1'2')2)2')3(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1(1(1(1... , ...2')2)2')2)2')2(1(1(1'2')2)2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(φ(Г0,ω),0) ~~ {n,n(1(1(1(1(1(1'2')2)2')1,2(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1(1(1'2')2)2')n(1'2')2)2')2(1'2')2)2}
φ(φ(Г0+1,0),0) ~~ {n,n(1(1(1(1(1(1'2')2)2')1'2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1(1(1'2')2)2')1(1(1(1'2')2)2')1... , ...2(1'2')2)2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(φ(ωГ0+1,0),0) ~~ {n,n(1(1(1(2(1(1'2')2)2')2(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1(1(1'2')2)2')1(1(1(1'2')2)2')...n раз...2(1'2')2)2}
φ(φ(ωГ0×2,0),0) ~~ {n,n(1(1(1(1(1(1'2')2)3')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1(1(1(1(1... , ...2')2)2')2)2(1(1'2')2)2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(φ(ωωГ0+1,0),0) ~~ {n,n(1(1(1(1(1(1'2')2)1,2')2(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1(1(1'2')2)n')2(1'2')2)2')2(1'2')2)2}
φ(φ(ωωГ0×2,0),0) ~~ {n,n(1(1(1(1(1(1'2')2)1(1(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1(1(1'2')2)1(1(1(1(1... , ...2')2)2')2)2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(φ(ωωωГ0+1,0),0) ~~ {n,n(1(1(1(1(2(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1(1(1'2')2)1(1(1'2')2)...n раз...2')2(1'2')2)2')2(1'2')2)2}
φ(φ(ωωωГ0+ω,0),0) ~~ {n,n(1(1(1(1(1,2(1'2')2)2')2(1'2')2)2')2(1'2')2)2} = {n,n(1(1(1(1(n(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
φ(φ(φ(1,Г0+1),0),0) ~~ {n,n(1(1(1(1(1'2(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1(1(1(1... , ...2(1'2')2)2(1'2')2)2(1'2')2)2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(φ(φ(ω,Г0+1),0),0) ~~ {n,n(1(1(1(1(1(2')2(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1(1'1'1'...n раз...2(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
φ(φ(φ(ωω,Г0+1),0),0) ~~ {n,n(1(1(1(1(1(1,2')2(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1(1(n')2(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
φ(φ(φ(Г0,1),0),0) ~~ {n,n(1(1(1(1(1(1(1(1'2')2)2')2(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1(1(1(1(1(1(1(1(1... , ...2')2)2')2)2')2(1'2')2)2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
Г1 = φ(1,0,1) ~~ {n,n(1(1'2')3)2} = {n,n(1(1(1(1(1(1(1(1... , ...2')2(1'2')2)2')2(1'2')2)2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(1,Г1+1) ~~ {n,n(1'2(1'2')3)2} = {n,n(1(1(1... , ...2(1'2')3)2(1'2')3)2(1'2')3)2} n-1 вложений
φ(ω,Г1+1) ~~ {n,n(1(2')2(1'2')3)2} = {n,n(1'1'1'...n раз...2(1'2')3)2}
φ(Г0,Г1+1) ~~ {n,n(1(1(1(1'2')2)2')2(1'2')3)2} = {n,n(1(1(1(1(1(1... , ...2')2)2')2)2')2(1'2')3)2} n-1 вложений
φ(Г1,1) ~~ {n,n(1(1(1(1'2')3)2')2(1'2')3)2}
= {n,n(1(1(1(1(1(1... , ...2')2(1'2')2)2')2(1'2')2)2')2(1'2')3)2} n-1 вложений
φ(Г1,2) ~~ {n,n(1(1(1(1'2')3)2')3(1'2')3)2}
= {n,n(1(1(1(1(1(1... , ...2')2(1'2')2)2')2(1'2')2)2')2(1(1(1'2')3)2')2(1'2')3)2} n-1 вложений
φ(Г1+1,0) ~~ {n,n(1(1(1(1'2')3)2')1'2(1'2')3)2}
= {n,n(1(1(1(1'2')3)2')1(1(1(1(1'2')3)2')1... , ...2(1'2')3)2(1'2')3)2} n-1 вложений
φ(Г1+Г0,0) ~~ {n,n(1(1(1(1'2')3)2')1(1(1(1'2')2)2')2(1'2')3)2}
= {n,n(1(1(1(1'2')3)2')1(1(1(1(1(1... , ...2')2)2')2)2')2(1'2')3)2} n-1 вложений
φ(Г1×2,0) ~~ {n,n(1(1(1(1'2')3)2')1(1(1(1'2')3)2')2(1'2')3)2}
= {n,n(1(1(1(1'2')3)2')1(1(1(1(1(1... , ...2')2(1'2')2)2')2(1'2')2)2')2(1'2')3)2} n-1 вложений
φ(ωГ1+1,0) ~~ {n,n(1(2(1(1'2')3)2')2(1'2')3)2} = {n,n(1(1(1(1'2')3)2')1(1(1(1'2')3)2')...n раз...2(1'2')3)2}
φ(ωГ1+Г0,0) ~~ {n,n(1(1(1(1'2')2)2(1(1'2')3)2')2(1'2')3)2}
= {n,n(1(1(1(1(1(1... , ...2')2)2')2)2(1(1'2')3)2')2(1'2')3)2} n-1 вложений
φ(ωГ1×2,0) ~~ {n,n(1(1(1(1'2')3)3')2(1'2')3)2}
= {n,n(1(1(1(1(1(1... , ...2')2(1'2')2)2')2(1'2')2)2(1(1'2')3)2')2(1'2')3)2} n-1 вложений
φ(ωωГ1+1,0) ~~ {n,n(1(1(1(1'2')3)1,2')2(1'2')3)2} = {n,n(1(1(1(1'2')3)n')2(1'2')3)2}
φ(ωωωГ1+1,0) ~~ {n,n(1(1(2(1'2')3)2')2(1'2')3)2} = {n,n(1(1(1(1'2')3)1(1(1'2')3)1(1(1'2')3)...n раз...2')2(1'2')3)2}
φ(ωωωГ1+ω,0) ~~ {n,n(1(1(1,2(1'2')3)2')2(1'2')3)2} = {n,n(1(1(n(1'2')3)2')2(1'2')3)2}
φ(φ(1,Г1+1),0) ~~ {n,n(1(1(1'2(1'2')3)2')2(1'2')3)2} = {n,n(1(1(1(1... , ...2(1'2')3)2(1'2')3)2')2(1'2')3)2} n-1 вложений
φ(φ(Г1,1),0) ~~ {n,n(1(1(1(1(1(1'2')3)2')2(1'2')3)2')2(1'2')3)2}
= {n,n(1(1(1(1(1(1(1(1... , ...2')2(1'2')2)2')2(1'2')2)2')2(1'2')3)2')2(1'2')3)2} n-1 вложений
φ(φ(φ(Г1,1),0),0) ~~ {n,n(1(1(1(1(1(1(1(1'2')3)2')2(1'2')3)2')2(1'2')3)2')2(1'2')3)2}
= {n,n(1(1(1(1(1(1(1(1(1(1... , ...2')2(1'2')2)2')(1'2')3)2')2(1'2')3)2')2(1'2')3)2')2(1'2')3)2} n-1 вложений
Г2 = φ(1,0,2) ~~ {n,n(1(1'2')4)2} = {n,n(1(1(1(1(1(1(1(1... , ...2')2(1'2')3)2')2(1'2')3)2')2(1'2')3)2')2(1'2')3)2} n-1 вложений
Гω = φ(1,0,ω) ~~ {n,n(1(1'2')1,2)2} = {n,n(1(1'2')n)2}
φ(1,0,ε0) ~~ {n,n(1(1'2')1(1'2)2)2} = {n,n(1(1'2')1(1(1(1... , ...2)2)2)2} n-1 вложений
φ(1,0,φ(ω,0)) ~~ {n,n(1(1'2')1(1(2')2)2)2} = {n,n(1(1'2')1(1'1'1'...n раз...2)2)2}
φ(1,0,φ(ε0,0)) ~~ {n,n(1(1'2')1(1(1(1'2)2')2)2)2} = {n,n(1(1'2')1(1(1(1(1(1... , ...2)2)2)2')2)2)2} n-1 вложений
φ(1,0,Г0) ~~ {n,n(1(1'2')1(1(1'2')2)2)2} = {n,n(1(1'2')1(1(1(1(1... , ...2')2)2')2)2)2} n-1 вложений
φ(1,0,Г0+1) ~~ {n,n(1(1'2')2(1(1'2')2)2)2} = {n,n(1(1(1(1... , ...2')2(1'2')1(1(1'2')2)2)2')2(1'2')1(1(1'2')2)2)2} n-1 вложений
φ(1,0,Г0×2) ~~ {n,n(1(1'2')1(1(1'2')2)3)2} = {n,n(1(1'2')1(1(1(1(1... , ...2')2)2')2)2(1(1'2')2)2)2} n-1 вложений
φ(1,0,ωГ0+1) ~~ {n,n(1(1'2')1(1(1'2')2)1,2)2} = {n,n(1(1'2')1(1(1'2')2)n)2}
φ(1,0,ωωГ0+1) ~~ {n,n(1(1'2')1(2(1'2')2)2)2} = {n,n(1(1'2')1(1(1'2')2)1(1(1'2')2)1(1(1'2')2)...n раз...2)2}
φ(1,0,Г1) ~~ {n,n(1(1'2')1(1(1'2')3)2)2} = {n,n(1(1'2')1(1(1(1(1... , ...2')2(1'2')2)2')2(1'2')2)2)2} n-1 вложений
φ(1,0,Г2) ~~ {n,n(1(1'2')1(1(1'2')4)2)2} = {n,n(1(1'2')1(1(1(1(1... , ...2')2(1'2')3)2')2(1'2')3)2)2} n-1 вложений
φ(1,0,φ(1,0,Г0)) ~~ {n,n(1(1'2')1(1(1'2')1(1(1'2')2)2)2)2} = {n,n(1(1'2')1(1(1'2')1(1(1(1(1... , ...2')2)2')2)2)2)2} n-1 вложений
φ(1,0,φ(1,0,φ(1,0,Г0))) ~~ {n,n(1(1'2')1(1(1'2')1(1(1'2')1(1(1'2')2)2)2)2)2}
= {n,n(1(1'2')1(1(1'2')1(1(1'2')1(1(1(1(1... , ...2')2)2')2)2)2)2)2} n-1 вложений
φ(1,1,0) ~~ {n,n(1(1'2')1'2)2} = {n,n(1(1'2')1(1(1'2')1(1(1'2')1(1(1'2')1... , ...2)2)2)2)2} n-1 вложений
φ(1,1,0)+1 ~~ {n,n,2(1(1'2')1'2)2} = {n,{n,...{n,n(1(1'2')1'2)2}...(1(1'2')1'2)2}(1(1'2')1'2)2} n-1 вложений
φ(1,1,0)×2 ~~ {n,n(1(1'2')1'2)3} = {n,n(1(1'2')1(1(1'2')1(1(1'2')1... , ...2)2)2)2(1(1'2')1'2)2} n-1 вложений
ωφ(1,1,0)+1 ~~ {n,n(1(1'2')1'2)1,2} = {n,n(1(1'2')1'2)n}
ωφ(1,1,0)×2 ~~ {n,n(1(1'2')1'2)1(1(1'2')1'2)2} = {n,n(1(1'2')1'2)1(1(1'2')1(1(1'2')1(1(1'2')1... , ...2)2)2)2} n-1 вложений
ωωφ(1,1,0)+1 ~~ {n,n(2(1'2')1'2)2} = {n,n(1(1'2')1'2)1(1(1'2')1'2)1(1(1'2')1'2)1...n-1 раз...2}
φ(1,0,φ(1,1,0)+1) ~~ {n,n(1(1'2')2'2)2} = {n,n(1(1(1(1(1(1... , ...2')2(1'2')1'2)2')2(1'2')1'2)2')2(1'2')1'2)2} n-1 вложений
φ(1,0,φ(1,1,0)×2) ~~ {n,n(1(1'2')1(1(1'2')1'2)2'2)2} = {n,n(1(1'2')1(1(1'2')1(1(1'2')1... , ...2)2)2'2)2} n-1 вложений
φ(1,0,ωφ(1,1,0)+1) ~~ {n,n(1(1'2')1(1(1'2')1'2)1,2'2)2} = {n,n(1(1'2')1(1(1'2')n'2)2'2)2}
φ(1,0,ωφ(1,1,0)×2) ~~ {n,n(1(1'2')1(1(1'2')1'2)1(1(1'2')1'2)2'2)2}
= {n,n(1(1'2')1(1(1'2')1'2)1(1(1'2')1(1(1'2')1... , ...2)2)2'2)2} n-1 вложений
φ(1,0,ωωφ(1,1,0)+1) ~~ {n,n(1(1'2')1(2(1'2')1'2)2'2)2} = {n,n(1(1'2')1(1(1'2')1'2)1(1(1'2')1'2)...n раз...2'2)2}
φ(1,0,φ(1,0,(1,1,0)+1)) ~~ {n,n(1(1'2')1(1(1'2')2'2)2'2)2} = {n,n(1(1'2')1(1(1(1'2')1(1(1'2')1... , ...2)2)2'2)2} n-1 вложений
φ(1,1,1) ~~ {n,n(1(1'2')1'3)2} = {n,n(1(1'2')1(1(1'2')1(1(1'2')1(1(1'2')1... , ...2'2)2'2)2'2)2'2)2} n-1 вложений
φ(1,2,0) ~~ {n,n(1(1'2')1'1'2)2} = {n,n(1(1'2')1'1(1(1'2')1'1(1(1'2')1'1... , ...2)2)2)2} n-1 вложений
φ(1,ω,0) ~~ {n,n(1(1'2')1(2')2)2} = {n,n(1(1'2')1'1'1'...n раз...2)2}
φ(1,ωω,0) ~~ {n,n(1(1'2')1(1,2')2)2} = {n,n(1(1'2')1(n')2)2}
φ(1,ε0,0) ~~ {n,n(1(1'2')1(1(1'2)2')2)2} = {n,n(1(1'2')1(1(1(1(1... , ...2)2)2)2')2)2} n-1 вложений
φ(1,Г0,0) ~~ {n,n(1(1'2')1(1(1(1'2')2)2')2)2} = {n,n(1(1'2')1(1(1(1(1(1... , ...2')2)2')2)2')2)2} n-1 вложений
φ(1,Г1,0) ~~ {n,n(1(1'2')1(1(1(1'2')3)2')2)2} = {n,n(1(1'2')1(1(1(1(1(1... , ...2')2(1'2')2)2')2(1'2')2)2')2)2} n-1 вложений
φ(1,φ(1,1,0),0) ~~ {n,n(1(1'2')1(1(1(1'2')1'2)2')2)2} = {n,n(1(1'2')1(1(1(1'2')1(1(1'2')1... , ...2)2)2')2)2} n-1 вложений
φ(1,φ(1,ω,0),0) ~~ {n,n(1(1'2')1(1(1(1'2')1(2')2)2')2)2} = {n,n(1(1'2')1(1(1(1'2')1'1'1'...n раз...2)2')2)2}
φ(1,φ(1,ωω,0),0) ~~ {n,n(1(1'2')1(1(1(1'2')1(1,2')2)2')2)2} = {n,n(1(1'2')1(1(1(1'2')1(n')2)2')2)2}
φ(1,φ(1,Г0,0),0) ~~ {n,n(1(1'2')1(1(1(1'2')1(1(1(1'2')2)2')2)2')2)2}
= {n,n(1(1'2')1(1(1(1'2')1(1(1(1(1(1... , ...2')2)2')2)2')2)2')2)2} n-1 вложений
φ(1,φ(1,φ(1,ωω,0),0),0) ~~ {n,n(1(1'2')1(1(1(1'2')1(1(1(1'2')1(1,2')2)2')2)2')2)2}
= {n,n(1(1'2')1(1(1(1'2')1(1(1(1'2')1(n')2)2')2)2')2)2}
φ(1,φ(1,φ(1,Г0,0),0),0) ~~ {n,n(1(1'2')1(1(1(1'2')1(1(1(1'2')1(1(1(1'2')2)2')2)2')2)2')2)2}
= {n,n(1(1'2')1(1(1(1'2')1(1(1(1'2')1(1(1(1(1(1... , ...2')2)2')2)2')2)2')2)2')2)2} n-1 вложений
φ(2,0,0) ~~ {n,n(1(1'2')1(1'2')2)2} = {n,n(1(1'2')1(1(1(1'2')1(1(1(1'2')1(1... , ...2')2)2')2)2')2)2} n-1 вложений
φ(1,φ(2,0,0)+1) ~~ {n,n(1'2(1'2')1(1'2')2)2} = {n,n(1(1... , ...2(1'2')1(1'2')2)2(1'2')1(1'2')2)2} n-1 вложений
φ(1,0,φ(2,0,0)+1) ~~ {n,n(1(1'2')2(1'2')2)2} = {n,n(1(1(1(1... , ...2')2(1'2')2(1'2')2)2')2(1'2')2(1'2')2)2} n-1 вложений
φ(1,1,φ(2,0,0)+1) ~~ {n,n(1(1'2')1'2(1'2')2)2} = {n,n(1(1'2')1(1(1'2')1... , ...2(1'2')2)2(1'2')2)2} n-1 вложений
φ(1,ω,φ(2,0,0)+1) ~~ {n,n(1(1'2')1(2')2(1'2')2)2} = {n,n(1(1'2')1'1'1'...n раз...2(1'2')2)2}
φ(1,ωω,φ(2,0,0)+1) ~~ {n,n(1(1'2')1(1,2')2(1'2')2)2} = {n,n(1(1'2')1(n')2(1'2')2)2}
φ(1,ε0,φ(2,0,0)+1) ~~ {n,n(1(1'2')1(1(1'2)2')2(1'2')2)2} = {n,n(1(1'2')1(1(1(1(1... , ...2)2)2)2')2(1'2')2)2} n-1 вложений
φ(1,Г0,φ(2,0,0)+1) ~~ {n,n(1(1'2')1(1(1(1'2')2)2')2(1'2')2)2} = {n,n(1(1'2')1(1(1(1(1(1... , ...2')2)2')2)2')2(1'2')2)2} n-1 вложений
φ(1,φ(2,0,0),1) ~~ {n,n(1(1'2')1(1(1(1'2')1(1'2')2)2')2(1'2')2)2}
= {n,n(1(1'2')1(1(1(1'2')1(1(1(1'2')1(1... , ...2')2)2')2)2')2(1'2')2)2} n-1 вложений
φ(1,φ(2,0,0),2) ~~ {n,n(1(1'2')1(1(1(1'2')1(1'2')2)2')3(1'2')2)2}
= {n,n(1(1'2')1(1(1(1'2')1(1(1(1'2')1(1... , ...2')2)2')2)2')2(1(1(1'2')1(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(1,φ(2,0,0)+1,0) ~~ {n,n(1(1'2')1(1(1(1'2')1(1'2')2)2')1'2(1'2')2)2}
= {n,n(1(1'2')1(1(1(1'2')1(1'2')2)2')1(1(1'2')1(1(1(1'2')1(1'2')2)2')... , ...2(1'2')2)2(1'2')2)2} n-1 вложений
φ(1,φ(2,0,0)×2,0) ~~ {n,n(1(1'2')1(1(1(1'2')1(1'2')2)2')1(1(1(1'2')1(1'2')2)2')2(1'2')2)2}
= {n,n(1(1'2')1(1(1(1'2')1(1'2')2)2')1(1(1(1'2')1(1(1(1'2')1(1... , ...2')2)2')2)2')2(1'2')2)2} n-1 вложений
φ(1,ωφ(2,0,0)+1,0) ~~ {n,n(1(1'2')1(2(1(1'2')1(1'2')2)2')2(1'2')2)2}
= {n,n(1(1'2')1(1(1(1'2')1(1'2')2)2')1(1(1(1'2')1(1'2')2)2')...n раз...2(1'2')2)2}
φ(1,ωφ(2,0,0)×2,0) ~~ {n,n(1(1'2')1(1(1(1'2')1(1'2')2)3')2(1'2')2)2}
= {n,n(1(1'2')1(1(1(1(1'2')1(1(1(1'2')1(1... , ...2')2)2')2)2(1(1'2')1(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(1,ωωφ(1,1,0)+1,0) ~~ {n,n(1(1'2')1(1(2(1'2')1(1'2')2)2')2(1'2')2)2}
= {n,n(1(1'2')1(1(1(1'2')1(1'2')2)1(1(1'2')1(1'2')2)...n раз...2')2(1'2')2)2}
φ(1,ωωφ(1,1,0)+ω,0) ~~ {n,n(1(1'2')1(1(1,2(1'2')1(1'2')2)2')2(1'2')2)2} = {n,n(1(1'2')1(1(n(1'2')1(1'2')2)2')2(1'2')2)2}
φ(1,φ(1,φ(2,0,0)+1),0) ~~ {n,n(1(1'2')1(1(1'2(1'2')1(1'2')2)2')2(1'2')2)2}
= {n,n(1(1'2')1(1(1(1... , ...2(1'2')1(1'2')2)2(1'2')1(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(1,φ(1,0,φ(2,0,0)+1),0) ~~ {n,n(1(1'2')1(1(1(1'2')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1'2')1(1(1(1(1(1... , ...2')2(1'2')2(1'2')2)2')2(1'2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(1,φ(1,φ(2,0,0),1),0) ~~ {n,n(1(1'2')1(1(1(1'2')1(1(1(1'2')1(1'2')2)2')2(1'2')2)2')2(1'2')2)2}
= {n,n(1(1'2')1(1(1(1'2')1(1(1(1'2')1(1(1(1'2')1(1... , ...2')2)2')2)2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(2,0,1) ~~ {n,n(1(1'2')1(1'2')3)2} = {n,n(1(1'2')1(1(1(1'2')1(1(1(1'2')1(1... , ...2')2(1'2')2)2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
φ(2,0,ω) ~~ {n,n(1(1'2')1(1'2')1,2)2} = {n,n(1(1'2')1(1'2')n)2}
φ(2,1,0) ~~ {n,n(1(1'2')1(1'2')1'2)2} = {n,n(1(1'2')1(1'2')1(1(1'2')1(1'2')1... , ...2)2)2} n-1 вложений
φ(3,0,0) ~~ {n,n(1(1'2')1(1'2')1(1'2')2)2} = {n,n(1(1'2')1(1'2')1(1(1(1'2')1(1'2')1(1... , ...2')2)2')2)2} n-1 вложений
φ(4,0,0) ~~ {n,n(1(1'2')1(1'2')1(1'2')1(1'2')2)2}
= {n,n(1(1'2')1(1'2')1(1'2')1(1(1(1'2')1(1'2')1(1'2')1(1... , ...2')2)2')2)2} n-1 вложений
φ(5,0,0) ~~ {n,n(1(1'2')1(1'2')1(1'2')1(1'2')1(1'2')2)2}
= {n,n(1(1'2')1(1'2')1(1'2')1(1'2')1(1(1(1'2')1(1'2')1(1'2')1(1'2')1(1... , ...2')2)2')2)2} n-1 вложений
φ(ω,0,0) ~~ {n,n(1(2'2')2)2} = {n,n(1(1'2')1(1'2')1(1'2')1(1'2')1(1'2')...n раз...2)2}
φ(1,φ(ω,0,0)+1) ~~ {n,n(1'2(2'2')2)2} = {n,n(1(1(1... , ...2(2'2')2)2(2'2')2)2(2'2')2)2} n-1 вложений
φ(1,0,φ(ω,0,0)+1) ~~ {n,n(1(1'2')2(2'2')2)2} = {n,n(1(1(1(1(1(1... , ...2')2(2'2')2)2')2(2'2')2)2')2(2'2')2)2} n-1 вложений
φ(2,0,φ(ω,0,0)+1) ~~ {n,n(1(1'2')1(1'2')2(2'2')2)2} = {n,n(1(1'2')1(1(1(1'2')1(1... , ...2')2(2'2')2)2')2(2'2')2)2} n-1 вложений
φ(ω,0,1) ~~ {n,n(1(2'2')3)2} = {n,n(1(1'2')1(1'2')1(1'2')1(1'2')1(1'2')...n раз...(2'2')2)2}
φ(ω,1,0) ~~ {n,n(1(2'2')1'2)2} = {n,n(1(2'2')1(1(2'2')1(1(2'2')1(1(2'2')1... , ...2)2)2)2)2} n-1 вложений
φ(ω+1,0,0) ~~ {n,n(1(2'2')1(1'2')2)2} = {n,n(1(2'2')1(1(1(2'2')1(1(1(2'2')1(1... , ...2')2)2')2)2')2)2} n-1 вложений
φ(ω×2,0,0) ~~ {n,n(1(2'2')1(2'2')2)2} = {n,n(1(2'2')1(1'2')1(1'2')1(1'2')1(1'2')...n раз...2)2}
φ(ω2,0,0) ~~ {n,n(1(3'2')2)2} = {n,n(1(2'2')1(2'2')1(2'2')1(2'2')1(2'2')...n раз...2)2}
φ(ωω,0,0) ~~ {n,n(1(1,2'2')2)2} = {n,n(1(n'2')2)2}
φ(ε0,0,0) ~~ {n,n(1(1(1'2)2'2')2)2} = {n,n(1(1(1(1(1... , ...2)2)2)2'2')2)2} n-1 вложений
φ(Г0,0,0) ~~ {n,n(1(1(1(1'2')2)2'2')2)2} = {n,n(1(1(1(1(1(1... , ...2')2)2')2)2'2')2)2} n-1 вложений
φ(φ(ω,0,0),0,0) ~~ {n,n(1(1(1(2'2')2)2'2')2)2} = {n,n(1(1(1(1'2')1(1'2')1(1'2')...n раз...2)2'2')2)2}
φ(φ(Г0,0,0),0,0) ~~ {n,n(1(1(1(1(1(1'2')2)2'2')2)2'2')2)2} = {n,n(1(1(1(1(1(1(1(1... , ...2')2)2')2)2'2')2)2'2')2)2} n-1 вложений
φ(φ(φ(ω,0,0),0,0),0,0) ~~ {n,n(1(1(1(1(1(2'2')2)2'2')2)2'2')2)2} = {n,n(1(1(1(1(1(1'2')1(1'2')1(1'2')...n раз...2)2'2')2)2'2')2)2}
φ(1,0,0,0) = ψ(ΩΩ2) ~~ {n,n(1(1'3')2)2} = {n,n(1(1(1(1(1(1(1(1... , ...2'2')2)2'2')2)2'2')2)2'2')2)2} n-1 вложений
φ(1,φ(1,0,0,0)+1) ~~ {n,n(1'2(1'3')2)2} = {n,n(1(1(1... , ...2(1'3')2)2(1'3')2)2(1'3')2)2} n-1 вложений
φ(1,0,φ(1,0,0,0)+1) ~~ {n,n(1(1'2')2(1'3')2)2} = {n,n(1(1(1(1(1(1... , ...2')2(1'3')2)2')2(1'3')2)2')2(1'3')2)2} n-1 вложений
φ(1,0,0,1) ~~ {n,n(1(1'3')3)2} = {n,n(1(1(1(1(1(1... , ...2'2)2(1'3')2)2'2)2(1'3')2)2'2)2(1'3')2)2} n-1 вложений
φ(1,0,1,0) ~~ {n,n(1(1'3')1'2)2} = {n,n(1(1'3')1(1(1'3')1(1(1'3')1... , ...2)2)2)2} n-1 вложений
φ(1,1,0,0) ~~ {n,n(1(1'3')1(1'2')2)2} = {n,n(1(1'3')1(1(1(1'3')1(1(1(1'3')1(1... , ...2')2)2')2)2')2)2} n-1 вложений
φ(2,0,0,0) ~~ {n,n(1(1'3')1(1'3')2)2} = {n,n(1(1'3')1(1(1(1'3')1(1(1(1'3')1(1... , ...2'2')2)2'2')2)2'2')2)2} n-1 вложений
φ(ω,0,0,0) ~~ {n,n(1(2'3')3)2} = {n,n(1(1'3')1(1'3')1(1'3')1(1'3')1(1'3')...n раз...2)2}
φ(ωω,0,0,0) ~~ {n,n(1(1,2'3')3)2} = {n,n(1(n'3')3)2}
φ(φ(1,0,0,0),0,0,0) ~~ {n,n(1(1(1(1'3')2)2'3')3)2} = {n,n(1(1(1(1(1(1(1(1... , ...2'2')2)2'2')2)2'2')2)2'3')3)2} n-1 вложений
φ(1,0,0,0,0) = ψ(ΩΩ3) ~~ {n,n(1(1'4')2)2} = {n,n(1(1(1(1(1(1(1(1... , ...2'3')2)2'3')2)2'3')2)2'3')2)2} n-1 вложений
φ(1,0,0,0,0,0) = ψ(ΩΩ4) ~~ {n,n(1(1'5')2)2} = {n,n(1(1(1(1(1(1(1(1... , ...2'4')2)2'4')2)2'4')2)2'4')2)2} n-1 вложений
φ(1ω) = ψ(ΩΩω) ~~ {n,n(1(1'1,2')2)2} = {n,n(1(1'n')2)2}
ψ(ΩΩω)+1 ~~ {n,n,2(1(1'1,2')2)2} = {n,{n,...{n,n(1(1'1,2')2)2}...(1(1'1,2')2)2}(1(1'1,2')2)2} n-1 вложений
ψ(ΩΩω)×2 ~~ {n,n(1(1'1,2')2)3} = {n,n(1(1'n')2)2(1(1'1,2')2)2}
ψ(ΩΩω)×ω = ψ(ΩΩω+1) ~~ {n,n(1(1'1,2')2)1,2} = {n,n(1(1'1,2')2)n}
ψ(ΩΩω)2 = ψ(ΩΩω+ψ(ΩΩω)) ~~ {n,n(1(1'1,2')2)1(1(1'1,2')2)2} = {n,n(1(1'1,2')2)1(1(1'n')2)2}
ψ(ΩΩω)ω = ψ(ΩΩω+ψ(ΩΩω+1)) ~~ {n,n(2(1'1,2')2)2} = {n,n(1(1'1,2')2)1(1(1'1,2')2)1(1(1'1,2')2)...n-1 раз...2}
ψ(ΩΩω+Ω) = εψ(ΩΩω)+1 ~~ {n,n(1'2(1'1,2')2)2} = {n,n(1(1(1... , ...2(1'1,2')2)2(1'1,2')2)2(1'1,2')2)2} n-1 вложений
ψ(ΩΩω+Ω2) ~~ {n,n(1'1'2(1'1,2')2)2} = {n,n(1'1(1'1(1'1... , ...2(1'1,2')2)2(1'1,2')2)2(1'1,2')2)2} n-1 вложений
ψ(ΩΩω+Ωω) ~~ {n,n(1(2')2(1'1,2')2)2} = {n,n(1'1'1'...n раз...2(1'1,2')2)2}
ψ(ΩΩω+Ωψ(ΩΩ)) ~~ {n,n(1(1(1(1'2')2)2')2(1'1,2')2)2} = {n,n(1(1(1(1(1(1... , ...2')2)2')2)2')2(1'1,2')2)2} n-1 вложений
ψ(ΩΩω+Ωψ(ΩΩω)) ~~ {n,n(1(1(1(1'1,2')2)2')2(1'1,2')2)2} = {n,n(1(1(1(1'n')2)2')2(1'1,2')2)2}
ψ(ΩΩω+Ωψ(ΩΩω)+1) ~~ {n,n(1(1(1(1'1,2')2)2')1'2(1'1,2')2)2}
= {n,n(1(1(1(1'1,2')2)2')1(1(1(1(1'1,2')2)2')1... , ...2(1'1,2')2)2(1'1,2')2)2} n-1 вложений
ψ(ΩΩω+Ωψ(ΩΩω+1)) ~~ {n,n(1(2(1(1'1,2')2)2')2(1'1,2')2)2}
= {n,n(1(1(1(1'1,2')2)2')1(1(1(1'1,2')2)2')...n раз...2(1'1,2')2)2}
ψ(ΩΩω+Ωψ(ΩΩω+ψ(ΩΩω))) ~~ {n,n(1(1(1(1'1,2')2)3')2(1'1,2')2)2} = {n,n(1(1(1(1'n')2)2(1(1'1,2')2)2')2(1'1,2')2)2}
ψ(ΩΩω+Ωψ(ΩΩω+ψ(ΩΩω+1))) ~~ {n,n(1(1(1(1'1,2')2)1,2')2(1'1,2')2)2} = {n,n(1(1(1(1'1,2')2)n')2(1'1,2')2)2}
ψ(ΩΩω+Ωψ(ΩΩω+ψ(ΩΩω+ψ(ΩΩω)))) ~~ {n,n(1(1(1(1'1,2')2)1(1(1'1,2')2)2')2(1'1,2')2)2}
= {n,n(1(1(1(1'1,2')2)1(1(1'n')2)2')2(1'1,2')2)2}
ψ(ΩΩω+Ωψ(ΩΩω+ψ(ΩΩω+ψ(ΩΩω+1)))) ~~ {n,n(1(1(2(1'1,2')2)2')2(1'1,2')2)2}
= {n,n(1(1(1(1'1,2')2)1(1(1'1,2')2)...n раз...2')2(1'1,2')2)2}
ψ(ΩΩω+Ωψ(ΩΩω+Ω)) ~~ {n,n(1(1(1'2(1'1,2')2)2')2(1'1,2')2)2}
= {n,n(1(1(1(1... , ...2(1'1,2')2)2(1'1,2')2)2')2(1'1,2')2)2} n-1 вложений
ψ(ΩΩω+Ωψ(ΩΩω+Ωψ(ΩΩ))) ~~ {n,n(1(1(1(1(1(1'2')2)2')2(1'1,2')2)2')2(1'1,2')2)2}
= {n,n(1(1(1(1(1(1(1(1... , ...2')2)2')2)2')2(1'1,2')2)2')2(1'1,2')2)2} n-1 вложений
ψ(ΩΩω+Ωψ(ΩΩω+Ωψ(ΩΩω))) ~~ {n,n(1(1(1(1(1(1'1,2')2)2')2(1'1,2')2)2')2(1'1,2')2)2}
= {n,n(1(1(1(1(1(1'n')2)2')2(1'1,2')2)2')2(1'1,2')2)2}
ψ(ΩΩω+ΩΩ) ~~ {n,n(1(1'2')2(1'1,2')2)2} = {n,n(1(1(1(1(1(1(1... , ...2')2(1'1,2')2)2')2(1'1,2')2)2')2(1'1,2')2)2} n-1 вложений
ψ(ΩΩω+ΩΩ+1) ~~ {n,n(1(1'2')1'2(1'1,2')2)2}
= {n,n(1(1'2')1(1(1'2')1(1(1'2')1... , ...2(1'1,2')2)2(1'1,2')2)2(1'1,2')2)2} n-1 вложений
ψ(ΩΩω+ΩΩ+ψ(ΩΩ)) ~~ {n,n(1(1'2')1(1(1(1'2')2)2')2(1'1,2')2)2}
= {n,n(1(1'2')1(1(1(1(1(1... , ...2')2)2')2)2')2(1'1,2')2)2} n-1 вложений
ψ(ΩΩω+ΩΩ+ψ(ΩΩω)) ~~ {n,n(1(1'2')1(1(1(1'1,2')2)2')2(1'1,2')2)2} = {n,n(1(1'2')1(1(1(1'n')2)2')2(1'1,2')2)2}
ψ(ΩΩω+ΩΩ×2) ~~ {n,n(1(1'2')1(1'2')2(1'1,2')2)2}
= {n,n(1(1'2')1(1(1(1'2')1(1(1(1'2')1(1... , ...2')2(1'1,2')2)2')2(1'1,2')2)2')2(1'1,2')2)2} n-1 вложений
ψ(ΩΩω+ΩΩ×ω) ~~ {n,n(1(2'2')2(1'1,2')2)2} = {n,n(1(1'2')1(1'2')1(1'2')...n раз...2(1'1,2')2)2}
ψ(ΩΩω+ΩΩ×ψ(ΩΩ)) ~~ {n,n(1(1(1(1'2')2)2'2')2(1'1,2')2)2} = {n,n(1(1(1(1(1(1... , ...2')2)2')2)2'2')2(1'1,2')2)2} n-1 вложений
ψ(ΩΩω+ΩΩ×ψ(ΩΩω)) ~~ {n,n(1(1(1(1'1,2')2)2'2')2(1'1,2')2)2} = {n,n(1(1(1(1'n')2)2'2')2(1'1,2')2)2}
ψ(ΩΩω+ΩΩ2) ~~ {n,n(1(1'3')2(1'1,2')2)2} = {n,n(1(1(1(1(1(1(1... , ...2'2')2(1'1,2')2)2'2')2(1'1,2')2)2'2')2(1'1,2')2)2} n-1 вложений
ψ(ΩΩω×2) ~~ {n,n(1(1'1,2')3)2} = {n,n(1(1'n')2(1'1,2')2)2}
ψ(ΩΩω×3) ~~ {n,n(1(1'1,2')4)2} = {n,n(1(1'n')2(1'1,2')3)2}
ψ(ΩΩω×ω) ~~ {n,n(1(1'1,2')1,2)2} = {n,n(1(1'1,2')n)2}
ψ(ΩΩω×ωω) ~~ {n,n(1(1'1,2')1(2)2)2} = {n,n(1(1'1,2')1,1,1,...n раз...2)2}
ψ(ΩΩω×ψ(Ω)) ~~ {n,n(1(1'1,2')1(1'2)2)2} = {n,n(1(1'1,2')1(1(1(1... , ...2)2)2)2)2} n-1 вложений
ψ(ΩΩω×ψ(ΩΩ)) ~~ {n,n(1(1'1,2')1(1(1'2')2)2)2} = {n,n(1(1'1,2')1(1(1(1(1... , ...2')2)2')2)2)2} n-1 вложений
ψ(ΩΩω×ψ(ΩΩω)) ~~ {n,n(1(1'1,2')1(1(1'1,2')2)2)2} = {n,n(1(1'1,2')1(1(1'n')2)2)2}
ψ(ΩΩω+1) ~~ {n,n(1(1'1,2')1'2)2} = {n,n(1(1'1,2')1(1(1'1,2')1(1(1'1,2')1... , ...2)2)2)2} n-1 вложений
ψ(ΩΩω+2) ~~ {n,n(1(1'1,2')1'1'2)2} = {n,n(1(1'1,2')1'1(1(1'1,2')1'1(1(1'1,2')1'1... , ...2)2)2)2} n-1 вложений
ψ(ΩΩω+ω) ~~{n,n(1(1'1,2')1(2')2)2} = {n,n(1(1'1,2')1'1'1'...n раз...2)2}
ψ(ΩΩω+ωω) ~~ {n,n(1(1'1,2')1(1,2')2)2} = {n,n(1(1'1,2')1(n')2)2}
ψ(ΩΩω+ψ(Ω)) ~~ {n,n(1(1'1,2')1(1(1'2)2')2)2} = {n,n(1(1'1,2')1(1(1(1(1... , ...2)2)2)2')2)2} n-1 вложений
ψ(ΩΩω+ψ(ΩΩ)) ~~ {n,n(1(1'1,2')1(1(1(1'2')2)2')2)2} = {n,n(1(1'1,2')1(1(1(1(1(1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩω+Ω) ~~ {n,n(1(1'1,2')1(1'2')2)2} = {n,n(1(1'1,2')1(1(1(1'1,2')1(1(1(1'1,2')1(1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩω+Ω2) ~~ {n,n(1(1'1,2')1(1'3')2)2} = {n,n(1(1'1,2')1(1(1(1'1,2')1(1(1(1'1,2')1(1... , ...2'2')2)2'2')2)2'2')2)2} n-1 вложений
ψ(ΩΩω×2) ~~ {n,n(1(1'1,2')1(1'1,2')2)2} = {n,n(1(1'1,2')1(1'n')2)2}
ψ(ΩΩω×3) ~~ {n,n(1(1'1,2')1(1'1,2')1(1'1,2')2)2} = {n,n(1(1'1,2')1(1'1,2')1(1'n')2)2}
ψ(ΩΩω×ω) ~~ {n,n(1(2'1,2')2)2} = {n,n(1(1'1,2')1(1'1,2')1(1'1,2')...n раз...2)2}
ψ(ΩΩω+1) ~~ {n,n(1(1'2,2')2)2} = {n,n(1(1(1(1(1(1(1(1... , ...2,2')2)2,2')2)2,2')2)2,2')2)2} n-1 вложений
ψ(ΩΩω+2) ~~ {n,n(1(1'3,2')2)2} = {n,n(1(1(1(1(1(1(1(1... , ...2'2,2')2)2'2,2')2)2'2,2')2)2'2,2')2)2} n-1 вложений
ψ(ΩΩω×2) ~~ {n,n(1(1'1,3')2)2} = {n,n(1(1'n,2')2)2}
ψ(ΩΩω2) ~~ {n,n(1(1'1,1,2')2)2} = {n,n(1(1'n,n')2)2}
ψ(ΩΩωω) ~~ {n,n(1(1'1(2)2')2)2} = {n,n(1(1'1,1,1,...n раз...2')2)2}
ψ(ΩΩψ(Ω)) ~~ {n,n(1(1'1(1'2)2')2)2} = {n,n(1(1'1(1(1(1... , ...2)2)2)2')2)2} n-1 вложений
ψ(ΩΩψ(ΩΩ)) ~~ {n,n(1(1'1(1(1'2')2)2')2)2} = {n,n(1(1'1(1(1(1(1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩψ(ΩΩ2)) ~~ {n,n(1(1'1(1(1'3')2)2')2)2} = {n,n(1(1'1(1(1(1(1... , ...2'2')2)2'2')2)2')2)2} n-1 вложений
ψ(ΩΩψ(ΩΩω)) ~~ {n,n(1(1'1(1(1'1,2')2)2')2)2} = {n,n(1(1'1(1(1'n')2)2')2)2}
ψ(ΩΩψ(ΩΩψ(ΩΩ))) ~~ {n,n(1(1'1(1(1'1(1(1'2')2)2')2)2')2)2} = {n,n(1(1'1(1(1'1(1(1(1(1... , ...2')2)2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩψ(ΩΩψ(ΩΩω))) ~~ {n,n(1(1'1(1(1'1(1(1'1,2')2)2')2)2')2)2} = {n,n(1(1'1(1(1'1(1(1'n')2)2')2)2')2)2}
ψ(ΩΩΩ) ~~ {n,n(1(1'1'2')2)2} = {n,n(1(1'1(1(1'1(1(1'1(1(1'1... , ...2')2)2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ)+1 ~~ {n,n,2(1(1'1'2')2)2} = {n,{n,...{n,n(1(1'1'2')2)2}...(1(1'1'2')2)2}(1(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ)×2 ~~ {n,n(1(1'1'2')2)3} = {n,n(1(1'1(1(1'1(1(1'1... , ...2')2)2')2)2')2)2(1(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ)×3 ~~ {n,n(1(1'1'2')2)4} = {n,n(1(1'1(1(1'1(1(1'1... , ...2')2)2')2)2')2)2(1(1'1'2')2)3} n-1 вложений
ψ(ΩΩΩ)×ω = ψ(ΩΩΩ+1) ~~ {n,n(1(1'1'2')2)1,2} = {n,n(1(1'1'2')2)n}
ψ(ΩΩΩ)2 ~~ {n,n(1(1'1'2')2)1(1(1'1'2')2)2} = {n,n(1(1'1'2')2)1(1(1'1(1(1'1(1(1'1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ)ω ~~ {n,n(2(1'1'2')2)2} = {n,n(1(1'1'2')2)1(1(1'1'2')2)1(1(1'1'2')2)...n-1 раз...2}
ψ(ΩΩΩ)ψ(ΩΩΩ) ~~ {n,n(1(1(1'1'2')2)2(1'1'2')2)2} = {n,n(1(1(1'1(1(1'1... , ...2')2)2')2)2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ)ψ(ΩΩΩ)2 ~~ {n,n(1(1(1'1'2')2)3(1'1'2')2)2} = {n,n(1(1(1'1(1(1'1... , ...2')2)2')2)2(1(1'1'2')2)2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ)ψ(ΩΩΩ)ω ~~ {n,n(1(1(1'1'2')2)1,2(1'1'2')2)2} = {n,n(1(1(1'1'2')2)n(1'1'2')2)2}
ψ(ΩΩΩ)ψ(ΩΩΩ)ψ(ΩΩΩ) ~~ {n,n(1(1(1'1'2')2)1(1(1'1'2')2)2(1'1'2')2)2}
= {n,n(1(1(1'1'2')2)1(1(1(1'1(1(1'1... , ...2')2)2')2)2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ)ψ(ΩΩΩ)ψ(ΩΩΩ)ω ~~ {n,n(1(2(1'1'2')2)2(1'1'2')2)2} = {n,n(1(1(1'1'2')2)1(1(1'1'2')2)...n раз...2(1'1'2')2)2}
ψ(ΩΩΩ)ψ(ΩΩΩ)ψ(ΩΩΩ)ψ(ΩΩΩ) ~~ {n,n(1(1(1(1'1'2')2)2(1'1'2')2)2(1'1'2')2)2}
= {n,n(1(1(1(1(1'1(1(1'1... , ...2')2)2')2)2(1'1'2')2)2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ)ψ(ΩΩΩ)ψ(ΩΩΩ)ψ(ΩΩΩ)ω ~~ {n,n(1(1(1(1'1'2')2)1,2(1'1'2')2)2(1'1'2')2)2} = {n,n(1(1(1(1'1'2')2)n(1'1'2')2)2(1'1'2')2)2}
ψ(ΩΩΩ)ψ(ΩΩΩ)ψ(ΩΩΩ)ψ(ΩΩΩ)ψ(ΩΩΩ) ~~ {n,n(1(1(1(1'1'2')2)1(1(1'1'2')2)2(1'1'2')2)2(1'1'2')2)2}
= {n,n(1(1(1(1'1'2')2)1(1(1'1(1(1'1... , ...2')2)2')2)2(1'1'2')2)2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ)ψ(ΩΩΩ)ψ(ΩΩΩ)ψ(ΩΩΩ)ψ(ΩΩΩ)ω ~~ {n,n(1(1(2(1'1'2')2)2(1'1'2')2)2(1'1'2')2)2}
= {n,n(1(1(1(1'1'2')2)1(1(1'1'2')2)...n раз...2(1'1'2')2)2(1'1'2')2)2}
ψ(ΩΩΩ+Ω) = εψ(ΩΩΩ)+1 ~~ {n,n(1'2(1'1'2')2)2} = {n,n(1(1(1... , ...2(1'1'2')2)2(1'1'2')2)2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ+Ω2) ~~ {n,n(1'1'2(1'1'2')2)2} = {n,n(1'1(1'1(1'1... , ...2(1'1'2')2)2(1'1'2')2)2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ+Ω3) ~~ {n,n(1'1'1'2(1'1'2')2)2} = {n,n(1'1'1(1'1'1(1'1'1... , ...2(1'1'2')2)2(1'1'2')2)2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ+Ωω) ~~ {n,n(1(2')2(1'1'2')2)2} = {n,n(1'1'1'...n раз...2(1'1'2')2)2}
ψ(ΩΩΩ+ΩΩ) ~~ {n,n(1(1'2')2(1'1'2')2)2} = {n,n(1(1(1(1(1(1(1... , ...2')2(1'1'2')2)2')2(1'1'2')2)2')2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ+ΩΩ×2) ~~ {n,n(1(1'2')1(1'2')2(1'1'2')2)2}
= {n,n(1(1'2')1(1(1(1'2')1(1(1(1'2')1(1... , ...2')2(1'1'2')2)2')2(1'1'2')2)2')2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ+ΩΩ×ω) ~~ {n,n(1(2'2')2(1'1'2')2)2} = {n,n(1(1'2')1(1'2')1(1'2')...n раз...2(1'1'2')2)2}
ψ(ΩΩΩ+ΩΩ2) ~~ {n,n(1(1'3')2(1'1'2')2)2} = {n,n(1(1(1(1(1(1(1... , ...2'2')2(1'1'2')2)2'2')2(1'1'2')2)2'2')2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ+ΩΩ3) ~~ {n,n(1(1'4')2(1'1'2')2)2} = {n,n(1(1(1(1(1(1(1... , ...2'3')2(1'1'2')2)2'3')2(1'1'2')2)2'3')2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ+ΩΩω) ~~ {n,n(1(1'1,2')2(1'1'2')2)2} = {n,n(1(1'n')2(1'1'2')2)2}
ψ(ΩΩΩ+ΩΩψ(Ω)) ~~ {n,n(1(1'1(1'2)2')2(1'1'2')2)2} = {n,n(1(1'1(1(1(1... , ...2)2)2)2')2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ+ΩΩψ(ΩΩ)) ~~ {n,n(1(1'1(1(1'2')2)2')2(1'1'2')2)2} = {n,n(1(1'1(1(1(1(1... , ...2')2)2')2)2')2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ+ΩΩψ(ΩΩω)) ~~ {n,n(1(1'1(1(1'1,2')2)2')2(1'1'2')2)2} = {n,n(1(1'1(1(1'n')2)2')2(1'1'2')2)2}
ψ(ΩΩΩ+ΩΩψ(ΩΩψ(ΩΩω))) ~~ {n,n(1(1'1(1(1'1(1(1'1,2')2)2')2)2')2(1'1'2')2)2} = {n,n(1(1'1(1(1'1(1(1'n')2)2')2)2')2(1'1'2')2)2}
ψ(ΩΩΩ+ΩΩψ(ΩΩΩ)) ~~ {n,n(1(1'1(1(1'1'2')2)2')2(1'1'2')2)2} = {n,n(1(1'1(1(1'1(1(1'1... , ...2')2)2')2)2')2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ+ΩΩψ(ΩΩΩ+ΩΩω)) ~~ {n,n(1(1'1(1(1'1,2')2(1'1'2')2)2')2(1'1'2')2)2} = {n,n(1(1'1(1(1'n')2(1'1'2')2)2')2(1'1'2')2)2}
ψ(ΩΩΩ+ΩΩψ(ΩΩΩ+ΩΩψ(ΩΩΩ))) ~~ {n,n(1(1'1(1(1'1(1(1'1'2')2)2')2(1'1'2')2)2')2(1'1'2')2)2}
= {n,n(1(1'1(1(1'1(1(1'1(1(1'1... , ...2')2)2')2)2')2(1'1'2')2)2')2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ×2) ~~ {n,n(1(1'1'2')3)2} = {n,n(1(1'1(1(1'1(1(1'1... , ...2')2(1'1'2')2)2')2(1'1'2')2)2')2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ×3) ~~ {n,n(1(1'1'2')4)2} = {n,n(1(1'1(1(1'1(1(1'1... , ...2')2(1'1'2')3)2')2(1'1'2')3)2')2(1'1'2')3)2} n-1 вложений
ψ(ΩΩΩ×ω) ~~ {n,n(1(1'1'2')1,2)2} = {n,n(1(1'1'2')n)2}
ψ(ΩΩΩ×ψ(ΩΩΩ)) ~~ {n,n(1(1'1'2')1(1(1'1'2')2)2)2} = {n,n(1(1'1'2')1(1(1'1(1(1'1... , ...2')2)2')2)2)2} n-1 вложений
ψ(ΩΩΩ×ψ(ΩΩΩ×ψ(ΩΩΩ))) ~~ {n,n(1(1'1'2')1(1(1'1'2')1(1(1'1'2')2)2)2)2}
= {n,n(1(1'1'2')1(1(1'1'2')1(1(1'1(1(1'1... , ...2')2)2')2)2)2)2} n-1 вложений
ψ(ΩΩΩ+1) ~~ {n,n(1(1'1'2')1'2)2} = {n,n(1(1'1'2')1(1(1'1'2')1(1(1'1'2')1... , ...2)2)2)2} n-1 вложений
ψ(ΩΩΩ+1×2) ~~ {n,n(1(1'1'2')1'3)2} = {n,n(1(1'1'2')1(1(1'1'2')1(1(1'1'2')1... , ...2'2)2'2)2'2)2} n-1 вложений
ψ(ΩΩΩ+2) ~~ {n,n(1(1'1'2')1'1'2)2} = {n,n(1(1'1'2')1'1(1(1'1'2')1'1(1(1'1'2')1'1... , ...2)2)2)2} n-1 вложений
ψ(ΩΩΩ+ω) ~~ {n,n(1(1'1'2')1(2')2)2} = {n,n(1(1'1'2')1'1'1'...n раз...2)2}
ψ(ΩΩΩ+ψ(Ω)) ~~ {n,n(1(1'1'2')1(1(1'2)2')2)2} = {n,n(1(1'1'2')1(1(1(1(1... , ...2)2)2)2')2)2} n-1 вложений
ψ(ΩΩΩ+ψ(ΩΩ)) ~~ {n,n(1(1'1'2')1(1(1(1'2')2)2')2)2} = {n,n(1(1'1'2')1(1(1(1(1(1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ+ψ(ΩΩΩ)) ~~ {n,n(1(1'1'2')1(1(1(1'1'2')2)2')2)2} = {n,n(1(1'1'2')1(1(1(1'1(1(1'1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ))) ~~ {n,n(1(1'1'2')1(1(1(1'1'2')1(1(1(1'1'2')2)2')2)2')2)2}
= {n,n(1(1'1'2')1(1(1(1'1'2')1(1(1(1'1(1(1'1... , ...2')2)2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ+Ω) ~~ {n,n(1(1'1'2')1(1'2')2)2} = {n,n(1(1'1'2')1(1(1(1'1'2')1(1(1(1'1'2')1(1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ+Ω×2) ~~ {n,n(1(1'1'2')1(1'2')3)2} = {n,n(1(1'1'2')1(1(1(1'1'2')1(1... , ...2')2(1'2')2)2')2(1'2')2)2} n-1 вложений
ψ(ΩΩΩ+Ω+1) ~~ {n,n(1(1'1'2')1(1'2')1'2)2} = {n,n(1(1'1'2')1(1'2')1(1(1'1'2')1(1'2')1... , ...2)2)2} n-1 вложений
ψ(ΩΩΩ+Ω+2) ~~ {n,n(1(1'1'2')1(1'2')1'1'2)2} = {n,n(1(1'1'2')1(1'2')1'1(1(1'1'2')1(1'2')1'1... , ...2)2)2} n-1 вложений
ψ(ΩΩΩ+Ω×2) ~~ {n,n(1(1'1'2')1(1'2')1(1'2')2)2} = {n,n(1(1'1'2')1(1'2')1(1(1(1'1'2')1(1'2')1(1... , ...2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ+Ω2) ~~ {n,n(1(1'1'2')1(1'3')2)2} = {n,n(1(1'1'2')1(1(1(1'1'2')1(1(1(1'1'2')1(1... , ...2'2')2)2'2')2)2'2')2)2} n-1 вложений
ψ(ΩΩΩ+Ω3) ~~ {n,n(1(1'1'2')1(1'4')2)2} = {n,n(1(1'1'2')1(1(1(1'1'2')1(1(1(1'1'2')1(1... , ...2'3')2)2'3')2)2'3')2)2} n-1 вложений
ψ(ΩΩΩ+Ωω) ~~ {n,n(1(1'1'2')1(1'1,2')2)2} = {n,n(1(1'1'2')1(1'n')2)2}
ψ(ΩΩΩ×2) ~~ {n,n(1(1'1'2')1(1'1'2')2)2} = {n,n(1(1'1'2')1(1'1(1(1'1'2')1(1'1... , ...2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ×2×2) ~~ {n,n(1(1'1'2')1(1'1'2')3)2} = {n,n(1(1'1'2')1(1'1(1(1'1'2')1(1'1... , ...2')2(1'1'2')2)2')2(1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ×2+1) ~~ {n,n(1(1'1'2')1(1'1'2')1'2)2} = {n,n(1(1'1'2')1(1'1'2')1(1(1'1'2')1(1'1'2')1... , ...2)2)2} n-1 вложений
ψ(ΩΩΩ×2+Ω) ~~ {n,n(1(1'1'2')1(1'1'2')1(1'2')2)2} = {n,n(1(1'1'2')1(1'1'2')1(1(1(1'1'2')1(1'1'2')1(1... , ...2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ×3) ~~ {n,n(1(1'1'2')1(1'1'2')1(1'1'2')2)2} = {n,n(1(1'1'2')1(1'1'2')1(1'1(1(1'1'2')1(1'1'2')1(1'1... , ...2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ×ω) ~~ {n,n(1(2'1'2')2)2} = {n,n(1(1'1'2')1(1'1'2')1(1'1'2')...n раз...2)2}
ψ(ΩΩΩ×ω2) ~~ {n,n(1(3'1'2')2)2} = {n,n(1(2'1'2')1(2'1'2')1(2'1'2')...n раз...2)2}
ψ(ΩΩΩ×ωω) ~~ {n,n(1(1,2'1'2')2)2} = {n,n(1(n'1'2')2)2}
ψ(ΩΩΩ×ψ(ΩΩΩ)) ~~ {n,n(1(1(1(1'1'2')2)2'1'2')2)2} = {n,n(1(1(1(1'1(1(1'1... , ...2')2)2')2)2'1'2')2)2} n-1 вложений
ψ(ΩΩΩ×ψ(ΩΩΩ×ψ(ΩΩΩ))) ~~ {n,n(1(1(1(1(1(1'1'2')2)2'1'2')2)2'1'2')2)2}
= {n,n(1(1(1(1(1(1'1(1(1'1... , ...2')2)2')2)2'1'2')2)2'1'2')2)2} n-1 вложений
ψ(ΩΩΩ+1) ~~ {n,n(1(1'2'2')2)2} = {n,n(1(1(1(1(1(1... , ...2'1'2')2)2'1'2')2)2'1'2')2)2} n-1 вложений
ψ(ΩΩΩ+1+1) ~~ {n,n(1(1'2'2')1'2)2} = {n,n(1(1'2'2')1(1(1'2'2')1(1(1'2'2')1... , ...2)2)2)2} n-1 вложений
ψ(ΩΩΩ+1+Ω) ~~ {n,n(1(1'2'2')1(1'2')2)2} = {n,n(1(1'2'2')1(1(1(1'2'2')1(1(1(1'2'2')1(1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ+1+ΩΩ) ~~ {n,n(1(1'2'2')1(1'1'2')2)2} = {n,n(1(1'2'2')1(1'1(1(1'2'2')1(1'1... , ...2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ+1×2) ~~ {n,n(1(1'2'2')1(1'2'2')2)2} = {n,n(1(1'2'2')1(1(1(1'2'2')1(1... , ...2'1'2')2)2'1'2')2)2} n-1 вложений
ψ(ΩΩΩ+1×ω) ~~ {n,n(1(2'2'2')2)2} = {n,n(1(1'2'2')1(1'2'2')1(1'2'2')...n раз...2)2}
ψ(ΩΩΩ+2) ~~ {n,n(1(1'3'2')2)2} = {n,n(1(1(1(1(1(1... , ...2'2'2')2)2'2'2')2)2'2'2')2)2} n-1 вложений
ψ(ΩΩΩ+ω) ~~ {n,n(1(1'1,2'2')2)2} = {n,n(1(1'n'2')2)2}
ψ(ΩΩΩ+ψ(ΩΩΩ)) ~~ {n,n(1(1'1(1(1'1'2')2)2'2')2)2} = {n,n(1(1'1(1(1'1(1(1'1... , ...2')2)2')2)2'2')2)2} n-1 вложений
ψ(ΩΩΩ+ψ(ΩΩΩ+ψ(ΩΩΩ))) ~~ {n,n(1(1'1(1(1'1(1(1'1'2')2)2'2')2)2'2')2)2}
= {n,n(1(1'1(1(1'1(1(1'1(1(1'1... , ...2')2)2')2)2'2')2)2'2')2)2} n-1 вложений
ψ(ΩΩΩ×2) ~~ {n,n(1(1'1'3')2)2} = {n,n(1(1'1(1(1'1(1(1'1... , ...2'2')2)2'2')2)2'2')2)2} n-1 вложений
ψ(ΩΩΩ×2×2) ~~ {n,n(1(1'1'3')3)2} = {n,n(1(1'1(1(1'1(1(1'1... , ...2'2')2(1'1'3')2)2'2')2(1'1'3')2)2'2')2(1'1'3')2)2} n-1 вложений
ψ(ΩΩΩ×2×ω) ~~ {n,n(1(1'1'3')1,2)2} = {n,n(1(1'1'n')1,2)2}
ψ(ΩΩΩ×2+1) ~~ {n,n(1(1'1'3')1'2)2} = {n,n(1(1'1'3')1(1(1'1'3')1(1(1'1'3')1... , ...2)2)2)2} n-1 вложений
ψ(ΩΩΩ×2×2) ~~ {n,n(1(1'1'3')1(1'1'3')2)2} = {n,n(1(1'1'3')1(1'1(1(1'1'3')1(1'1... , ...2'2')2)2'2')2)2} n-1 вложений
ψ(ΩΩΩ×2×ω) ~~ {n,n(1(2'1'3')2)2} = {n,n(1(1'1'3')1(1'1'3')1(1'1'3')...n раз...2)2}
ψ(ΩΩΩ×2+1) ~~ {n,n(1(1'2'3')2)2} = {n,n(1(1(1(1(1(1... , ...2'1'3')2)2'1'3')2)2'1'3')2)2} n-1 вложений
ψ(ΩΩΩ×3) ~~ {n,n(1(1'1'4')2)2} = {n,n(1(1'1(1(1'1(1(1'1... , ...2'3')2)2'3')2)2'3')2)2} n-1 вложений
ψ(ΩΩΩ×ω) ~~ {n,n(1(1'1'1,2')2)2} = {n,n(1(1'1'n')2)2}
ψ(ΩΩΩ×ψ(ΩΩΩ)) ~~ {n,n(1(1'1'1(1(1'1'2')2)2')2)2} = {n,n(1(1'1'1(1(1'1(1(1'1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ×ψ(ΩΩΩ×ψ(ΩΩΩ))) ~~ {n,n(1(1'1'1(1(1'1'1(1(1'1'2')2)2')2)2')2)2}
= {n,n(1(1'1'1(1(1'1'1(1(1'1(1(1'1... , ...2')2)2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ2) ~~ {n,n(1(1'1'1'2')2)2} = {n,n(1(1'1'1(1(1'1'1(1(1'1'1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ2+1) ~~ {n,n(1(1'1'1'2')1'2)2} = {n,n(1(1'1'1'2')1(1(1'1'1'2')1(1(1'1'1'2')1... , ...2)2)2)2} n-1 вложений
ψ(ΩΩΩ2+Ω) ~~ {n,n(1(1'1'1'2')1(1'2')2)2} = {n,n(1(1'1'1'2')1(1(1(1'1'1'2')1(1(1(1'1'1'2')1(1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ2+ΩΩ) ~~ {n,n(1(1'1'1'2')1(1'1'2')2)2} = {n,n(1(1'1'1'2')1(1'1(1(1'1'1'2')1(1'1... , ...2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ2+ΩΩ+1) ~~ {n,n(1(1'1'1'2')1(1'2'2')2)2} = {n,n(1(1'1'1'2')1(1(1(1'1'1'2')1(1... , ...2'1'2')2)2'1'2')2)2} n-1 вложений
ψ(ΩΩΩ2+ΩΩ×2) ~~ {n,n(1(1'1'1'2')1(1'1'3')2)2} = {n,n(1(1'1'1'2')1(1'1(1(1'1'1'2')1(1'1... , ...2'2')2)2'2')2)2} n-1 вложений
ψ(ΩΩΩ2×2) ~~ {n,n(1(1'1'1'2')1(1'1'1'2')2)2} = {n,n(1(1'1'1'2')1(1'1'1(1(1'1'1'2')1(1'1'1... , ...2')2)2')2)2} n-1 вложений
ψ(ΩΩΩ2×ω) ~~ {n,n(1(2'1'1'2')2)2} = {n,n(1(1'1'1'2')1(1'1'1'2')1(1'1'1'2')...n раз...2)2} n-1 вложений
ψ(ΩΩΩ2+1) ~~ {n,n(1(1'2'1'2')2)2} = {n,n(1(1(1(1(1(1... , ...2'1'1'2')2)2'1'1'2')2)2'1'1'2')2)2} n-1 вложений
ψ(ΩΩΩ2+Ω) ~~ {n,n(1(1'1'2'2')2)2} = {n,n(1(1'1(1(1'1(1(1'1... , ...2'1'2')2)2'1'2')2)2'1'2')2)2} n-1 вложений
ψ(ΩΩΩ2+Ω×2) ~~ {n,n(1(1'1'3'2')2)2} = {n,n(1(1'1(1(1'1(1(1'1... , ...2'2'2')2)2'2'2')2)2'2'2')2)2} n-1 вложений
ψ(ΩΩΩ2×2) ~~ {n,n(1(1'1'1'3')2)2} = {n,n(1(1'1'1(1(1'1'1(1(1'1'1... , ...2'2')2)2'2')2)2'2')2)2} n-1 вложений
ψ(ΩΩΩ2×ω) ~~ {n,n(1(1'1'1'1,2')2)2} = {n,n(1(1'1'1'n')2)2}
ψ(ΩΩΩ3) ~~ {n,n(1(1'1'1'1'2')2)2} = {n,n(1(1'1'1'1(1(1'1'1'1(1(1'1'1'1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩω) ~~ {n,n(1(1(2')2')2)2} = {n,n(1(1'1'1'...n раз...2')2)2}
ψ(ΩΩΩω+1) ~~ {n,n(1(1'2(2')2')2)2} = {n,n(1(1(1(1(1(1... , ...2(2')2')2)2(2')2')2)2(2')2')2)2} n-1 вложений
ψ(ΩΩΩω+Ω) ~~ {n,n(1(1'1'2(2')2')2)2} = {n,n(1(1'1(1(1'1(1(1'1... , ...2(2')2')2)2(2')2')2)2(2')2')2)2} n-1 вложений
ψ(ΩΩΩω+Ω2) ~~ {n,n(1(1'1'1'2(2')2')2)2} = {n,n(1(1'1'1(1(1'1'1(1(1'1'1... , ...2(2')2')2)2(2')2')2)2(2')2')2)2} n-1 вложений
ψ(ΩΩΩω×2) ~~ {n,n(1(1(2')3')2)2} = {n,n(1(1'1'1'...n раз...2(2')2')2)2}
ψ(ΩΩΩω+1) ~~ {n,n(1(1(2')1'2')2)2} = {n,n(1(1(2')1(1(1(2')1(1(1(2')1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩω×2) ~~ {n,n(1(1(2')1(2')2')2)2} = {n,n(1(1(2')1'1'1'...n раз...2')2)2}
ψ(ΩΩΩω2) ~~ {n,n(1(1(3')2')2)2} = {n,n(1(1(2')1(2')1(2')...n раз...2')2)2} n-1 вложений
ψ(ΩΩΩωω) ~~ {n,n(1(1(1,2')2')2)2} = {n,n(1(1(n')2')2)2}
ψ(ΩΩΩψ(ΩΩΩ)) ~~ {n,n(1(1(1(1(1'1'2')2)2')2')2)2} = {n,n(1(1(1(1(1'1(1(1'1... , ...2')2)2')2)2')2')2)2} n-1 вложений
ψ(ΩΩΩψ(ΩΩΩω)) ~~ {n,n(1(1(1(1(1(2')2')2)2')2')2)2} = {n,n(1(1(1(1(1'1'1'...n раз...2')2)2')2')2)2}
ψ(ΩΩΩψ(ΩΩΩψ(ΩΩΩ))) ~~ {n,n(1(1(1(1(1(1(1(1'1'2')2)2')2')2)2')2')2)2}
= {n,n(1(1(1(1(1(1(1(1'1(1(1'1... , ...2')2)2')2)2')2')2)2')2')2)2} n-1 вложений
ψ(ΩΩΩΩ) ~~ {n,n(1(1(1'2')2')2)2} = {n,n(1(1(1(1(1(1(1(1(1... , ...2')2')2)2')2')2)2')2')2)2} n-1 вложений
ψ(ΩΩΩΩ×2) ~~ {n,n(1(1(1'2')2')3)2} = {n,n(1(1(1(1(1(1(1(1... , ...2')2')2(1'2')2')2)2')2')2(1'2')2')2)2} n-1 вложений
ψ(ΩΩΩΩ×ω) ~~ {n,n(1(1(1'2')2')1,2)2} = {n,n(1(1(1'2')2')n)2}
ψ(ΩΩΩΩ+1) ~~ {n,n(1(1(1'2')2')1'2)2} = {n,n(1(1(1'2')2')1(1(1(1'2')2')1(1(1(1'2')2')1... , ...2)2)2)2} n-1 вложений
ψ(ΩΩΩΩ×2) ~~ {n,n(1(1(1'2')2')1(1(1'2')2')2)2} = {n,n(1(1(1'2')2')1(1(1(1(1(1'2')2')1(1(1... , ...2')2')2)2')2')2)2} n-1 вложений
ψ(ΩΩΩΩ×ω) ~~ {n,n(1(2(1'2')2')2)2} = {n,n(1(1(1'2')2')1(1(1'2')2')1(1(1'2')2')...n раз...2)2}
ψ(ΩΩΩΩ+1) ~~ {n,n(1(1'2(1'2')2')2)2} = {n,n(1(1(1(1(1(1... , ...2(1'2')2')2)2(1'2')2')2)2(1'2')2')2)2} n-1 вложений
ψ(ΩΩΩΩ+2) ~~ {n,n(1(1'3(1'2')2')2)2} = {n,n(1(1(1(1(1(1... , ...2'2(1'2')2')2)2'2(1'2')2')2)2'2(1'2')2')2)2} n-1 вложений
ψ(ΩΩΩΩ+ω) ~~ {n,n(1(1'1,2(1'2')2')2)2} = {n,n(1(1'n(1'2')2')2)2}
ψ(ΩΩΩΩ+Ω) ~~ {n,n(1(1'1'2(1'2')2')2)2} = {n,n(1(1'1(1(1'1(1(1'1... , ...2(1'2')2')2)2(1'2')2')2)2(1'2')2')2)2} n-1 вложений
ψ(ΩΩΩΩ+Ωω) ~~ {n,n(1(1(2')2(1'2')2')2)2} = {n,n(1(1'1'1'...n раз...2(1'2')2')2)2}
ψ(ΩΩΩΩ+Ωωω) ~~ {n,n(1(1(1,2')2(1'2')2')2)2} = {n,n(1(1(n')2(1'2')2')2)2}
ψ(ΩΩΩΩ×2) ~~ {n,n(1(1(1'2')3')2)2} = {n,n(1(1(1(1(1(1(1(1(1... , ...2')2(1'2')2')2)2')2(1'2')2')2)2')2(1'2')2')2)2} n-1 вложений
ψ(ΩΩΩΩ×ω) ~~ {n,n(1(1(1'2')1,2')2)2} = {n,n(1(1(1'2')n')2)2}
ψ(ΩΩΩΩ+1) ~~ {n,n(1(1(1'2')1'2')2)2} = {n,n(1(1(1'2')1(1(1(1'2')1(1(1(1'2')1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩΩ+2) ~~ {n,n(1(1(1'2')1'1'2')2)2} = {n,n(1(1(1'2')1'1(1(1(1'2')1'1(1(1(1'2')1'1... , ...2')2)2')2)2')2)2} n-1 вложений
ψ(ΩΩΩΩ+ω) ~~ {n,n(1(1(1'2')1(2')2')2)2} = {n,n(1(1(1'2')1'1'1'...n раз...2')2)2}
ψ(ΩΩΩΩ×2) ~~ {n,n(1(1(1'2')1(1'2')2')2)2} = {n,n(1(1(1'2')1(1(1(1(1'2')1(1(1(1(1'2')1(1... , ...2')2')2)2')2')2)2')2')2)2} n-1 вложений
ψ(ΩΩΩΩ×ω) ~~ {n,n(1(1(2'2')2')2)2} = {n,n(1(1(1'2')1(1'2')1(1'2')...n раз...2')2)2}
ψ(ΩΩΩΩ2) ~~ {n,n(1(1(1'3')2')2)2} = {n,n(1(1(1(1(1(1(1(1(1... , ...2'2')2')2)2'2')2')2)2'2')2')2)2} n-1 вложений
ψ(ΩΩΩΩω) ~~ {n,n(1(1(1'1,2')2')2)2} = {n,n(1(1(1'n')2')2)2}
ψ(ΩΩΩΩψ(ΩΩΩΩ))) ~~ {n,n(1(1(1'1(1(1(1'2')2')2)2')2')2)2} = {n,n(1(1(1'1(1(1(1(1(1(1... , ...2')2')2)2')2')2)2')2')2)2} n-1 вложений
ψ(ΩΩΩΩΩ) ~~ {n,n(1(1(1'1'2')2')2)2} = {n,n(1(1(1'1(1(1(1'1(1(1(1'1... , ...2')2')2)2')2')2)2')2')2)2} n-1 вложений
ψ(ΩΩΩΩΩω) ~~ {n,n(1(1(1(2')2')2')2)2} = {n,n(1(1(1'1'1'...n раз...2')2')2)2}
ψ(6Ω) ~~ {n,n(1(1(1(1'2')2')2')2)2} = {n,n(1(1(1(1(1(1(1(1(1(1(1(1... , ...2')2')2')2)2')2')2')2)2')2')2')2)2} n-1 вложений
ψ(7Ω) ~~ {n,n(1(1(1(1'1'2')2')2')2)2} = {n,n(1(1(1(1'1(1(1(1(1'1(1(1(1(1'1... , ...2')2')2')2)2')2')2')2)2')2')2')2)2} n-1 вложений
ψ(8Ω) ~~ {n,n(1(1(1(1(1'2')2')2')2')2)2} = {n,n(1(1(1(1(1(1(1(1(1(1... , ...2')2')2')2')2)2')2')2')2')2)2} n-1 вложений
ψ(9Ω) ~~ {n,n(1(1(1(1(1'1'2')2')2')2')2)2} = {n,n(1(1(1(1(1'1(1(1(1(1(1'1... , ...2')2')2')2')2)2')2')2')2')2)2} n-1 вложений
ψ(nΩ) ~~ {n,n(1(1(1(1(1(1... (1'2') ...2')2')2')2')2')2)2 - где (n-2)/2 вложений для четных n; n > 1
ψ(nΩ) ~~ {n,n(1(1(1(1(1(1... (1'1'2') ...2')2')2')2')2')2)2} - где (n-3)/2 вложений для нечетных n; n > 1
Что же, получился весьма гигантский список сопоставлений. Конечно, вот так, глядя на эти преобразования блуждающих разделителей первичного расширения среди цифр (в основном среди единиц и двоек), сложно осознать масштабы рекурсий. Именно поэтому мы так досконально разбирали ординальные функции, и если уж вы их освоили и можете ориентироваться в ординальных рекурсиях, то тогда эти сопоставления расскажут вам об истинных масштабах Первично расширяющейся массивной нотации намного больше.
На этом я заканчиваю третью часть книги и в четвертой мы продолжим заниматься тем же самым - наращивать рекурсии, а у любых рекурсий любого уровня сложности главный принцип - это самовложение во все что уже было на предыдущих уровнях, поэтому перед тем как переходить к четвертой части еще раз убедитесь, что вы достаточно усвоили материал изложенный здесь, потому что без его понимания дальше продвигаться будет очень сложно.
следующая часть...